Как можно найти ускорение без времени

Существует формула, с помощью которой можно посчитать путь, пройденный телом, когда нам известны его начальная скорость, ускорение и конечная скорость.

Сокращенно эту формулу называют «путь без времени». Так ее называют потому, что в правой ее части время t движения отсутствует (рис. 1).

Формула пути без времени помогает упростить решение некоторых задач кинематики. Особенно, задач, части C.

Однако, не торопитесь на ЕГЭ записывать эту формулу в готовом виде. Сначала в решении задачи нужно записать вывод этой формулы. И только потом ее можно использовать.

Формулу выводят из выражений для равнопеременного движения. Сейчас я помогу вам вывести эту формулу с помощью нескольких простых шагов.

Выводим формулу пути без времени

Для определенности будем считать, что тело движется по прямой все быстрее и быстрее. То есть, скорость тела увеличивается, так как появляется ускорение.

В таком случае векторы ускорения и скорости тела будут сонаправленными (параллельными и направленными в одну и ту же сторону).

Сонаправленные или противоположно направленные векторы называют коллинеарными векторами. Прочитайте подробнее о коллинеарных векторах.

Чтобы вычислить путь тела, когда скорость его увеличивается, нужно использовать две формулы:

[ large begin{cases} S  = v_{0} cdot t + displaystylefrac{a}{2} cdot t^{2} \ v  = v_{0} + a cdot t end{cases} ]

( large v_{0} left( frac{text{м}}{c} right)) – начальная скорость тела;

( large v left( frac{text{м}}{c} right)) – конечная скорость;

( large a left( frac{text{м}}{c^{2}} right)) – ускорение тела;

( large S left( text{м} right)) – путь, пройденный телом;

(large t left( c right)) – время, за которое тело прошло этот путь.

В формуле для пути S присутствует время t. Получим из нее формулу для пути, в которой время будет отсутствовать.

Что сделать, чтобы получить формулу пути, в которой отсутствует время:

• сначала получить выражение для времени t из уравнения для скорости;
•  затем в формулу пути подставить полученное выражение вместо времени t.

Выражаем время из формулы для скорости

Выпишем формулу, связывающую начальную и конечную скорость тела:

[ large v  = v_{0} + a cdot t ]

Избавимся в правой части от начальной скорости, обозначенной символом ( v_{0}). Для этого из обеих частей уравнения вычтем число ( v_{0}). Получим такую запись:

[ large v — v_{0} = a cdot t ]

Теперь, чтобы справа в формуле оставалось только время «t», избавимся от ускорения «a». Для этого разделим обе части уравнения на «a»:

[ large frac{ v — v_{0}}{a} = t ]

Это выражение нам пригодится для дальнейшего вывода формулы «путь без времени».

В формулу пути подставим выражение для времени

Запишем теперь формулу для пути S и полученную формулу для времени t, объединив их в систему:

[ large begin{cases} S  = v_{0}cdot t + displaystyle frac{a}{2}cdot t^{2}\ displaystyle frac{v — v_{0}}{a} = t end{cases} ]

В первом уравнении системы будем заменять символ t дробью из второго уравнения. Тогда система из двух уравнений превратится в единственное уравнение. И в этом уравнении не будет символа t времени:

[large S = v_{0} cdot frac{ v — v_{0}}{a} + frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]

Осталось теперь упростить полученное выражение. Будем производить упрощение по частям.

Упрощаем выражение, расположенное до знака «плюс» в правой части

Выпишем отдельно все, что располагается до знака «плюс» в правой части уравнения:

[large v_{0} cdot frac{ v — v_{0}}{a} ]

Умножим числитель дроби на число (v_{0}).

Для этого:

• сначала числитель обособим скобками;
• затем запишем число (v_{0}) перед скобками;
• а потом внесем это число внутрь скобок.

В числитель дроби, обособленный с помощью скобок помещаем число (v_{0}):

[large v_{0} cdot frac{ (v — v_{0})}{a} = frac{ v_{0} cdot (v — v_{0})}{a} ]

Теперь необходимо умножить скобку на число (v_{0}).  На рисунке 2 указано, как правильно выражение в скобках умножить на число, стоящее за скобками.

Нужно к каждой скорости в скобках дописать число (v_{0}), умножая его на эти скорости. Получим такое выражение:

[large frac{ v_{0} cdot (v — v_{0})}{a} = frac{ (v_{0} cdot v — v_{0} cdot v_{0})}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} ]

То есть, вместо первоначальной записи, мы получили такую запись:

[large v_{0} cdot frac{ (v — v_{0})}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} ]

Возводим в квадрат дробь

После знака «плюс» в правой части уравнения располагается дробь, которую нужно возвести в квадрат. Обратим внимание на эту дробь:

[large left( frac{ v — v_{0}}{a} right)^{2}]

Правильно возвести дробь в степень поможет рисунок 3.

В результате возведения в квадрат дробь приобретет такой вид:

[large left( frac{ v — v_{0}}{a} right)^{2} = frac{ (v — v_{0})^{2}}{a^{2}}]

В числителе этой дроби находится выражение в скобках, которое нужно возвести в квадрат. И нам придется применить одну из формул сокращенного умножения. Запоминать формулы сокращенного умножения удобно в виде, приведенном на рисунке 4.

Используем для этого формулу сокращенного умножения, которая содержит знак «минус». Она называется «Квадрат разности». Тогда числитель дроби превратится в такую запись:

[large ( v — v_{0})^{2} = (v^{2} + v^{2}_{0} — 2vv_{0})]

Теперь можем записать полученную дробь:

[large frac{ (v — v_{0})^{2}}{a^{2}} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}} ]

Упрощаем правую часть, записанную после знака «плюс»

Обратим внимание на все, что располагается в правой части уравнения после знака «плюс»:

[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]

Мы уже провели некоторые преобразования и можем теперь заменить дробь, возводимую в квадрат более подробной записью:

[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2} = frac{a}{2} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}}]

Примечание: Когда мы умножаем одну дробь на другую, то можем менять местами знаменатели этих дробей.

Итак, поменяем местами знаменатели дробей:

[large frac{a}{2} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{a^{2}} = frac{a}{a^{2}} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2}]

Теперь видно, что мы можем сократить ускорение и еще немного упростить выражение:

[large frac{a}{a^{2}} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2} = frac{1}{a} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2}]

А перемножив числители и знаменатели двух дробей, получим такую запись:

[large frac{1}{a} cdot frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Теперь, первоначальную дробь можно заменить дробью, полученной в ходе преобразований:

[large frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2} = frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Мы закончили преобразовывать выражения, содержащиеся в правой части уравнения после знака «плюс».

Теперь, осталось сложить две дроби в правой части – дробь, записанную до знака «плюс» с дробью, записанной после знака «плюс». А чтобы эти дроби можно было сложить, нужно будет привести их к общему знаменателю.

Приводим к общему знаменателю дроби в правой части уравнения

Вернемся еще раз к первоначальному уравнению:

[large S = v_{0} cdot frac{ v — v_{0}}{a} + frac{a}{2} cdot left( frac{ v — v_{0}}{a} right)^{2}]

Заменим правую часть этого уравнения выражениями, которые мы получили:

[large S = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} + frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Сравним знаменатели дробей.

Первая дробь обладает знаменателем «a», а вторая – «2a». Выберем число «2a» в качестве общего знаменателя обеих дробей.

Чтобы первую дробь привести к общему знаменателю «2a», умножим ее на единицу:

[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot 1]

Примечания:

1. Нам известно, что если какое-либо число умножить на единицу, то после умножения это число не изменится. Значит, если какое-либо выражение умножить на единицу, то полученное выражение останется равным самому себе. На единицу можно умножать все, что угодно – дроби, выражения в скобках и т. п.
2. Математики часто применяют прием умножения на единицу. А после этого единицу записывают в виде некоторой дроби. При этом используют правило: Единица – это дробь, у которой числитель и знаменатель равны (одинаковые).

Так как снизу в первой дроби не хватает числа 2, то единицу представим в виде дроби 2/2:

[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot 1 = frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot frac{2}{2}]

Получим такую дробь:

[large frac{ (v_{0} cdot v – v^{2}_{0} )}{a} cdot frac{2}{2} = frac{ 2(v_{0} cdot v – v^{2}_{0} )}{2a} ]

Поместим ее в выражение для пути:

[large S = frac{ 2(v_{0} cdot v – v^{2}_{0} )}{2a} + frac{(v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Дроби с одинаковыми знаменателями складываем

Теперь знаменатели дробей равны. И мы можем записать эти дроби под общим знаменателем:

[large S = frac{ 2(v_{0} cdot v – v^{2}_{0} ) + (v^{2} + v^{2}_{0} — 2vv_{0})}{2a}]

Раскроем скобки в числителе полученного выражения:

[large S = frac{ 2v_{0} v – 2v^{2}_{0} + v^{2} + v^{2}_{0} — 2vv_{0}}{2a}]

Примечание: Обратим внимание на то, что в числителе дважды встречается член (2v_{0} v), обладающий различными знаками. В начале числителя – знаком «плюс», а в конце числителя – знаком «минус». Это означает, что из числа (2v_{0}v) вычитается такое же число (2vv_{0}). В конце концов, это число покидает нашу запись и, она упрощается:

[large S = frac{ – 2v^{2}_{0} + v^{2} + v^{2}_{0}}{2a}]

Перепишем выражение, записав все, что содержит знак «плюс» в начало числителя:

[large S = frac{ v^{2} + v^{2}_{0} – 2v^{2}_{0}}{2a}]

Вычтем подобные члены, содержащие ( v^{2}_{0}):

[large v^{2}_{0} – 2v^{2}_{0} = – v^{2}_{0} ]

В результате получим короткую запись. Именно о ней говорят, когда имеется ввиду формула пути без времени:

[large boxed{ S = frac{ v^{2} — v^{2}_{0}}{2a} }]

Примечания:

1. Это формула, с помощью которой можно рассчитать путь тела, когда известны его начальная и конечная скорость, а, так же, ускорение.
2. Видно, что время t в правой части этого выражения отсутствует.
3. Мы выводили эту формулу для случая, когда тело увеличивало скорость.

Как выглядит формула пути без времени, когда скорость тела уменьшается

Если скорость тела будет уменьшаться, формулу для вычисления пути нужно будет переписать в таком виде:

[large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]

Получить такую формулу можно, проделав все шаги, описанные выше. Попробуйте самостоятельно ее получить. Выводить формулу нужно, используя формулы для уменьшающейся скорости:

[ large begin{cases} S  = v_{0} cdot t — displaystyle frac{a}{2} cdot t^{2} \ v  = v_{0} — a cdot t end{cases} ]

Выводы

Пусть нам известны начальная и конечная скорость тела и его ускорение. Тогда путь, пройденный телом, можно рассчитать так:

1. Когда движение равноускоренное и скорость тела увеличивается: [large boxed{ S = frac{ v^{2} — v^{2}_{0}}{2a} }]
2. А когда движение равнозамедленное и скорость уменьшается: [large boxed{ S = frac{ v^{2}_{0} — v^{2}}{2a} }]

Была ли эта статья полезной?

Равноускоренное
прямолинейное движение – движение по
прямой с постоянным ускорением (а = const
).

Ускорение
а (размерность: м/с²)
– векторная физическая величина,
показывающая, на сколько изменяется
скорость тела за 1 с.

В
векторном виде:

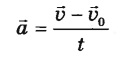
В
проекции на ось ОХ формула аналогичная

Знаки
проекции ускорения зависят от направления
вектора ускорения и оси – сонаправлены
они или направлены противоположно.

Измерительный
прибор – акселерометр. (В
ЕГЭ по физике есть вопросы, каким прибором
что измеряют.)

График
ускорения –
зависимость проекции ускорения от
времени:

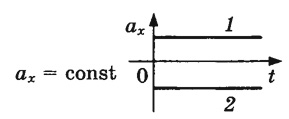
График
ускорения при равноускоренном
прямолинейном движении –
прямая, параллельная оси времени (1,
2).

Чем
дальше график от оси времени (2), тем
больше модуль ускорения.

Мгновенная
скорость – скорость в данный момент
времени или
в данном месте пространства.

Скорость
при равноускоренном прямолинейном
движении.

В
векторном виде,

в проекции на ось OX,

с
учетом знака ускорения («+» разгон, «-»
торможение):

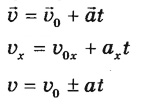
График
мгновенной скорости – зависимость
проекции скорости от времени.

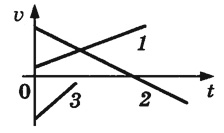
График
скорости при равноускоренном
прямолинейном движении –
прямая (1,
2, 3). Если
график располагается над осью времени,
то тело движется по направлению оси ОХ.

Чем
больше угол наклона графика (3), тем
больше модуль ускорения.

Если
график пересекает ось времени (2),
то на первом этапе тело тормозило, в
какой-то момент скорость его стала
равной нулю, и далее тело двигалось
ускоренно в противоположную сторону.

Геометрический
смысл перемещения

Модуль
перемещения при равноускоренном
прямолинейном движенииравен площади
трапеции под графиком скорости.

Формулы для
определения кинематических величин
равноускоренного прямолинейного
движения:

«Без
ускорения»
и «без
времени»
означает, что в этих формулах не фигурирует
ускорение и время, но это не значит, что
ускорение равно нулю. 

Цветом
выделены основные формулы,
остальные легко выводятся из них. 

Уравнение координаты при
равноускоренном прямолинейном движении
позволяет определить кинематические
величины равноускоренного прямолинейного
движения даже в тех случаях, когда
направление движения меняется:

5.2 Задача

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #