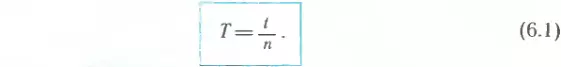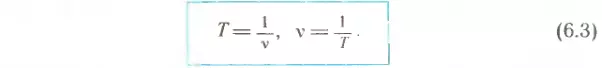Как можно найти период обращения - AvtoShod.ru - решение различных проблем

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения — это время, за которое совершается один оборот.

Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле

Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.

Другой характеристикой равномерного движения по окружности является частота обращения.

Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле

Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с^-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.

Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому

Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l_окр = 2πr, где π≈3,14— число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,

Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.

Видео, не по теме но интересно

1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?

Источник

Период обращения — Время, за которое тело совершает один оборот, т.е. поворачивается на угол 2 пи, называется периодом обращения

$LARGE T=frac{2pi }{omega }=frac{1}{n }$

Сидерические периоды обращения планет Солнечной системы:

Найдем период обращения:

Если, например, за время t = 4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой Т и определяется по формуле

$Large T=frac{1}{n }$

Найдем частоту обращения:

Если, например, за время t = 4 с тело совершило n = 20 оборотов,то за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой V (читается: ню) и определяется по формуле:

$Large omega =frac{n}{T}$

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с-1 (читается: секунда в минус первой степени).

В формуле мы использовали :

— Период обращения

— Частота обращения

— Число оборотов

Источник

Период вращения (обращения) — это минимальное время, за которое тело совершает один полный оборот, т.е. поворачивается на угол 2π

Для нахождения периода вращения надо время всех оборотов разделить на количество оборотов:

Период вращения — величина, обратная частоте вращения:

Единица измерения периода вращения (обращения) — секунда [1с]

Так как промежутку времени T соответствует угол поворота 2π, то период вращния можно поределить по формуле:

Обозначения:

T — период вращения

N — количество оборотов

t — время, за которое было совершено N оборотов

ν — частота вращения (обращения)

ω — угловая скорость

Источник

Как найти период обращения

Период обращения тела, которое движется по замкнутой траектории можно измерить при помощи часов. Если же обращение происходит слишком быстро, это делается после изменения некоторого числа полных обращений. Если тело вращается по окружности, и известна его линейная скорость, эта величина рассчитывается по формуле. Период обращения планеты рассчитывается по третьему закону Кеплера.

Вам понадобится

— секундомер;
— калькулятор;
— справочные данные по орбитам планет.

Инструкция

Измерьте при помощи секундомера время, требующееся вращающемуся телу, чтобы прийти в исходную точку. Это и будет период его вращения. Если измерить вращения тела затруднительно, то измерьте время t, N полных обращений. Найдите отношение этих величин, это и будет период вращения данного тела T (T=t/N). Период измеряется в тех же величинах, что и время. В интернациональной системе измерения это секунда.

Если известна частота вращения тела, то найдите период, поделив число 1 на значение частоты ν (T=1/ν).

Если тело вращается по круговой траектории и известна его линейная скорость, рассчитайте период его вращения. Для этого измерьте радиус R траектории, по которой вращается тело. Убедитесь, что модуль скорости не изменяется со временем. Затем произведите расчет. Для этого поделите длину окружности, по которой движется тело, которая равна 2∙π∙R (π≈3,14), на скорость его вращения v. Результатом будет период вращения данного тела по окружности T=2∙π∙R/v.

Если нужно рассчитать период обращения планеты, которая движется вокруг звезды, используйте третий закон Кеплера. Если две планеты вращаются вокруг одной звезды, то квадраты периодов их обращения относятся как кубы больших полуосей их орбит. Если обозначить периоды обращения двух планет T1 и T2, большие полуоси орбит (они эллиптичные), соответственно, a1 и a2, то T1²/ T2²= a1³/a2³. Данные расчеты верны в том случае, если массы планет значительно уступают массе звезды.

Пример: Определите период обращения планеты Марс. Чтобы рассчитать эту величину, найдите длину большей полуоси орбиты Марса, a1 и Земли, a2 (как планеты, которая тоже вращается вокруг Солнца). Они равны a1=227,92∙10^6 км и a2=149,6∙10^6 км. Период вращения земли T2=365,25 суток (1 земной год). Тогда найдите период обращения марса, преобразовав формулу из третьего закона Кеплера, для определения периода вращения Марса Т1=√( T2²∙ a1³/a2³)=√( 365,25²∙ (227,92∙10^6)³/(149,6∙10^6)³)≈686,86 суток.

Источники:

как найти обращения в тексте

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.

Источник

Не разобрался в теме? Освой физику с репетитором

1. Равномерное движение по окружности

Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.

Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.

Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Таким образом,

Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке.

Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.

Повышай свои знания с «Репетиторами Украины»

Выбери преподавателя для подготовки к экзаменам и контрольным работам

2. Период вращения и вращающаяся частота

Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.

Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.

Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.

При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

$[T = frac{t}{N}.]$

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: . Итак,

$[nu = frac{l}{T} = frac{2 pi R}{T}.]$

Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:

частота вращения равна количеству полных оборотов за одну секунду.

Частота вращения и период обращения связаны следующим соотношением:

$[nu=frac{1}{T}]$

Частоту в СИ измеряют в

$[frac{1}{c}(c^{-1})]$

3. Вращательное движение

В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.

Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.

Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

ПРОВЕРЬТЕ СЕБЯ

Приведите два-три примера криволинейного движения.
Приведите два-три примера равномерного движения по кругу.
Что такое вращательное движение? Приведите примеры такого движения.
Как направлена мгновенная скорость при движении по кругу Приведите два-три примера.

1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня. Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.

2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением: $nu=frac{1}{T}$ Частоту в СИ измеряют в обратных секундах.

3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

Источник

Видео, не по теме но интересно

Период вращения (обращения) — это минимальное время, за которое тело совершает один полный оборот, т.е. поворачивается на угол 2π

Как найти период обращения

Не пропустите также: