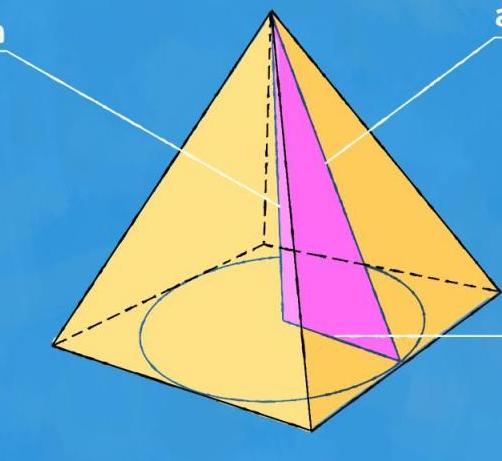
Как найти апофему
Апофемой в пирамиде называют отрезок, проведенный из ее вершины к основанию одной из боковых граней, если отрезок перпендикулярен этому основанию. Боковая грань такой объемной фигуры всегда имеет треугольную форму. Поэтому при необходимости вычисления длины апофемы допустимо использование свойств как многогранника (пирамиды), так и многоугольника (треугольника).
В треугольнике боковой грани апофема (f) является высотой, поэтому при известной длине бокового ребра (b) и угле (γ) между ним и ребром, на которое опущена апофема, можно использовать известную формулу вычисления высоты треугольника. Умножьте заданную длину ребра на синус известного угла: f = b*sin(γ). Эта формула применима к пирамидам любой (правильной или неправильной) формы.
Для вычисления каждой из трех апофем (f) правильной треугольной пирамиды достаточно знать всего один параметр — длину ребра (a). Это объясняется тем, что грани такой пирамиды имеют форму равносторонних треугольников одинаковых размеров. Для нахождения высот каждого из них вычислите половину произведения длины ребра на квадратный корень из трех: f = a*√3/2.
Если известна площадь (s) боковой грани пирамиды, в дополнение к ней достаточно знать длину (a) общего ребра этой грани с основанием объемной фигуры. В этом случае длину апофемы (f) находите удвоением соотношения между площадью и длиной ребра: f = 2*s/a.
Зная общую площадь поверхности пирамиды (S) и периметр ее основания (p) тоже можно вычислить апофему (f), но только для многогранника правильной формы. Удвойте площадь поверхности и разделите результат на периметр: f = 2*S/p. Форма основания в этом случае не имеет значения.
Количество вершин или сторон основания (n) нужно знать в том случае, если в условиях даны длина ребра (b) боковой грани и величина угла (α), который образуют два смежных боковых ребра правильной пирамиды. При таких исходных условиях вычисляйте апофему (f) умножением числа сторон основания на синус известного угла и возведенную в квадрат длину бокового ребра с последующим делением полученной величины пополам: f = n*sin(α)*b²/2.
В правильной пирамиде с четырехугольным основанием для нахождения длины апофемы (f) можно использовать высоту многогранника (H) и длину ребра основания (a). Извлеките квадратный корень из суммы возведенной в квадрат высоты и четверти от возведенной в квадрат длины ребра: f = √(H²+a²/4).
У треугольной пирамиды и в основании находится треугольник, и боковые грани являются треугольниками. То есть, апофема треугольной пирамиды — это обычная высота треугольника, который является боковой гранью.
Если речь о правильной пирамиде, то все боковые грани таковой являются равнобедренными треугольниками. Потому высота, проведенная к основанию, является медианой и биссектрисой.
Поэтому апофема определяется по теореме Пифагора, где ребро является гипотенузой, половина основания является первым катетом, а апофема — вторым.
Или же рассчитываем апофему, зная площадь боковой грани и основания: S= ah/2, h = 2S/a.
Как найти апофему
Апофемой в пирамиде называют отрезок, проведенный из ее вершины к основанию одной из боковых граней, если отрезок перпендикулярен этому основанию. Боковая грань такой объемной фигуры всегда имеет треугольную форму. Поэтому при необходимости вычисления длины апофемы допустимо использование свойств как многогранника (пирамиды), так и многоугольника (треугольника).

Вам понадобится
- — геометрические параметры пирамиды.
Инструкция
В треугольнике боковой грани апофема (f) является высотой, поэтому при известной длине бокового ребра (b) и угле (γ) между ним и ребром, на которое опущена апофема, можно использовать известную формулу вычисления высоты треугольника. Умножьте заданную длину ребра на синус известного угла: f = b*sin(γ). Эта формула применима к пирамидам любой (правильной или неправильной) формы.
Для вычисления каждой из трех апофем (f) правильной треугольной пирамиды достаточно знать всего один параметр — длину ребра (a). Это объясняется тем, что грани такой пирамиды имеют форму равносторонних треугольников одинаковых размеров. Для нахождения высот каждого из них вычислите половину произведения длины ребра на квадратный корень из трех: f = a*√3/2.
Если известна площадь (s) боковой грани пирамиды, в дополнение к ней достаточно знать длину (a) общего ребра этой грани с основанием объемной фигуры. В этом случае длину апофемы (f) находите удвоением соотношения между площадью и длиной ребра: f = 2*s/a.
Зная общую площадь поверхности пирамиды (S) и периметр ее основания (p) тоже можно вычислить апофему (f), но только для многогранника правильной формы. Удвойте площадь поверхности и разделите результат на периметр: f = 2*S/p. Форма основания в этом случае не имеет значения.
Количество вершин или сторон основания (n) нужно знать в том случае, если в условиях даны длина ребра (b) боковой грани и величина угла (α), который образуют два смежных боковых ребра правильной пирамиды. При таких исходных условиях вычисляйте апофему (f) умножением числа сторон основания на синус известного угла и возведенную в квадрат длину бокового ребра с последующим делением полученной величины пополам: f = n*sin(α)*b²/2.
В правильной пирамиде с четырехугольным основанием для нахождения длины апофемы (f) можно использовать высоту многогранника (H) и длину ребра основания (a). Извлеките квадратный корень из суммы возведенной в квадрат высоты и четверти от возведенной в квадрат длины ребра: f = √(H²+a²/4).
Войти на сайт
или
Забыли пароль?
Еще не зарегистрированы?
This site is protected by reCAPTCHA and the Google Privacy Policy and Terms of Service apply.
Вы решили изучить тонкости стереометрии, которые широко встречаются в решении различных задач. Для этого нужно усвоить огромное количество материала и свойств фигур, начиная от изучения планиметрии и заканчивая правильными пирамидами.
Особое внимание следует уделить правильной пирамиде, так как она часто встречается в задачах на объемные фигуры. Правильная пирамида имеет основание в форме правильного многоугольника, а ее вершина спроецирована в центр основания. Это свойство является очень важным при решении задач на объем.
Одним из ключевых понятий, которые нужно знать при изучении многоугольника, является апофема. Апофема — это отрезок, проведенный от вершины пирамиды до центра основания. Знание апофемы позволяет легко вычислять объемы и решать задачи на объемные фигуры.
Изучение стереометрических фигур может казаться сложным и объемным процессом. Однако, знание правильных понятий и свойств фигур, таких как правильная пирамида и апофема, помогут решать задачи быстро и легко. Не откладывайте свое изучение стереометрии на потом, ведь знание этой темы может пригодиться во многих сферах нашей жизни.»
Как вы уже поняли, в геометрии понятие апофемы — это широко распространенное явление. Невозможно узнать некоторые измерения пирамиды без знания этого. Само слово «апофема» — это пришедшее к нам из греческого языка явление, и переводится оно как «откладываю».
«Галоперидол» представляет собой лекарство, которое используется медицинскими работниками…
Определение апофемы
Апофема в планиметрии — это перпендикуляр, который проведен к стороне правильного многоугольника из его центра. Длина апофемы также проходит через центр многоугольника и равна расстоянию между центром и стороной многоугольника.
В стереометрии апофема пирамиды — это высота, которая проведена к основанию из боковой грани. Она используется только для правильных пирамид, то есть тех, у которых все грани являются равнобедренными и равносторонними треугольниками.
В случае правильной треугольной пирамиды апофема представляет собой высоту грани, которая представлена равнобедренным треугольником. Это значит, что высота, проведенная из вершины треугольной грани, делит ее на две равные части, а также является перпендикуляром к основанию пирамиды.
Какова роль апофемы
Апофема — это очень важный элемент пирамиды, потому что с ее помощью можно решить огромное количество задач. В частности, боковая поверхность правильной пирамиды равна полупроизведению периметра основания и апофемы грани.
Sбп = (Pосн*h)/2; h — апофема, это ее ключевая роль.
Не путайте с H (высота объемной фигуры в стереометрии).
Также, благодаря знанию апофемы, можно найти площадь грани как равнобедренного треугольника.
Свойства апофемы
Их мало, но все же их нужно помнить. В целом это следствия, вытекающие из определения. Итак, апофема в правильной пирамиде:
- Опущена на сторону основания под углом 90 градусов.
- Делит сторону, на которую опущена, пополам, так как является высотой в равнобедренном/равностороннем треугольнике и по совместительству — медианой.
В правильной пирамиде все апофемы равны, так как все ее боковые грани также одинаковые. При нахождении длины апофемы вам придется воспользоваться как свойствами многоугольника, так и свойствами многогранника. Как же найти числовое значение апофемы в правильной пирамиде?
Одно из заболеваний желудочно-кишечного тракта – бульбит. Это болезнь 12-перстной кишки, и она…
Как найти апофему пирамиды
Ее можно найти, применяя все ранее полученные знания, вот всего лишь несколько примеров:
- Если известны боковое ребро и сторона основания. Так как апофема делит сторону основания пополам и образует с ней угол в 90 градусов, то найти ее из прямоугольного треугольника по теореме Пифагора вам не составит труда. Также можно найти апофему, используя знания соотношений в прямоугольном треугольнике.
- Если известен радиус вписанной окружности в основание правильной пирамиды и высота всей фигуры. Радиус, проведенный к точке касания, перпендикулярен касательной, и апофема перпендикулярна этой стороне основания (которая является касательной к вписанной окружности). Высота фигуры перпендикулярна основанию и попадает в центр окружности, вписанной в основание пирамиды. Следовательно, радиус и высота фигуры являются катетами и образуют прямой угол, а вместе с апофемой — прямоугольный треугольник. И опять же по теореме Пифагора или через соотношения в прямоугольном треугольнике вы легко найдете апофему.
- Также если дана площадь грани и известно основание.
Когда вы сталкиваетесь с задачей нахождения апофемы, важно помнить, что вам потребуется использовать основные законы и правила планиметрии. Если вы не знакомы с некоторыми элементами из этого списка, то можете пользоваться уже известными параметрами и, шаг за шагом, находить недостающие данные для нахождения апофемы. Важно уметь уверенно оперировать различными фигурами и их характеристиками, чтобы успешно решить задачу. Мы надеемся, что предоставленная информация поможет вам освоить эту интересную тему и получить нужный результат в решении задач.
Пирамида — это пространственный полиэдр, или многогранник, который встречается в геометрических задачах. Основными свойствами этой фигуры являются ее объем и площадь поверхности, которые вычисляются из знания любых двух ее линейных характеристик. Одной из таких характеристик является апофема пирамиды. О ней пойдет речь в статье.
Фигура пирамида
Прежде чем приводить определение апофемы пирамиды, познакомимся с самой фигурой. Пирамида представляет собой многогранник, который образован одним n-угольным основанием и n треугольниками, составляющими боковую поверхность фигуры.
Всякая пирамида имеет вершину — точку соединения всех треугольников. Перпендикуляр, проведенный из этой вершины к основанию, называется высотой. Если высота пересекает в геометрическом центре основание, то фигура называется прямой. Пирамида прямая, имеющая равностороннее основание, называется правильной. На рисунке показана пирамида с шестиугольным основанием, на которую смотрят со стороны грани и ребра.
Апофема правильной пирамиды
Ее также называют апотемой. Под ней понимают перпендикуляр, проведенный из вершины пирамиды к стороне основания фигуры. По своему определению этот перпендикуляр соответствует высоте треугольника, который образует боковую грань пирамиды.
Поскольку мы рассматриваем пирамиду правильную с n-угольным основанием, то все n апофем для нее будут одинаковыми, поскольку таковыми являются равнобедренные треугольники боковой поверхности фигуры. Заметим, что одинаковые апофемы являются свойством правильной пирамиды. Для фигуры общего типа (наклонной с неправильным n-угольником) все n апофем будут разными.
Еще одним свойством апофемы пирамиды правильной является то, что она одновременно является высотой, медианой и биссектрисой соответствующего треугольника. Это означает, что она делит его на два одинаковых прямоугольных треугольника.
Треугольная пирамида и формулы для определения ее апофемы
В любой правильной пирамиде важными линейными характеристиками являются длина стороны ее основания, ребро боковое b, высота h и апофема hb. Эти величины друг с другом связаны соответствующими формулами, которые можно получить, если начертить пирамиду и рассмотреть необходимые прямоугольные треугольники.
Правильная треугольная пирамида состоит из 4 треугольных граней, причем одна из них (основание) должна быть обязательно равносторонней. Остальные являются равнобедренными в общем случае. Апофему треугольной пирамиды можно определить через другие величины по следующим формулам:
hb = √(b2 — a2/4);
hb = √(a2/12 + h2)
Первое из этих выражений справедливо для пирамиды с любым правильным основанием. Второе выражение характерно исключительно для треугольной пирамиды. Оно показывает, что апофема всегда больше высоты фигуры.
Не следует путать апофему пирамиды с таковой для многогранника. В последнем случае апофемой называется перпендикулярный отрезок, проведенный к стороне многогранника из его центра. Например, апофема равностороннего треугольника равна √3/6*a.
Задача на вычисление апофемы
Пусть дана правильная пирамида с треугольником в основании. Необходимо вычислить ее апофему, если известно, что площадь этого треугольника равна 34 см2, а сама пирамида состоит из 4 одинаковых граней.
В соответствии с условием задачи мы имеем дело с тетраэдром, состоящим из равносторонних треугольников. Формула для площади одной грани имеет вид:
S = √3/4*a2
Откуда получаем длину стороны a:
a = 2*√(S/√3)
Для определения апофемы hb воспользуемся формулой, содержащей боковое ребро b. В рассматриваемом случае его длина равна длине основания, имеем:
hb = √(b2 — a2/4) = √3/2*a
Подставляя значение a через S, получим конечную формулу:
hb = √3/2*2*√(S/√3) = √(S*√3)
Мы получили простую формулу, в которой апофема пирамиды зависит только от площади ее основания. Если подставить значение S из условия задачи, то получим ответ: hb ≈ 7,674 см.