Как ее составить напишите задачи на отношения

Текстовые задачи на отношения

Отношения встречаются в различных задачах и важно понимать, как с ними работать. Отношение – это какая-то уже сокращенная дробь. То есть данные в заданиях отношения – не реальная величина, а уже сокращенная, и мы должны узнать, на сколько.

Отношение = дробь, можно сокращать и расширять.

Если это тяжело принять, то можно поступить проще: представить, что в отношениях даны не величины, а какие-то деления. Отношение обычно записывается через двоеточие, например 3:5.

Например, рассматриваем отношение конфет на двух столах – представляем, что единицы отношения – это вазочки с одинаковым количеством конфет, мы должны узнать, сколько вазочек находится на одном столе, а сколько – на другом; если рассматриваем отношение цветов, то единицы отношения – это клумбы с одинаковым количеством цветов.

Пример 1

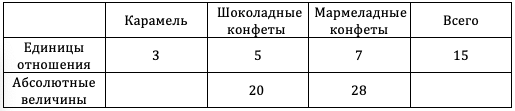
В магазине в наличии есть карамель, шоколадные конфеты и мармеладные конфеты в соотношении (3:5:7) соответственно.

1. Каково отношение между карамелью и шоколадными конфетами?​

Необходимо поделить количество коробок с карамелью на количество коробок с шоколадными конфетами, то есть (3:5).

2. Каково отношение между карамелью и мармеладными конфетами?​

Необходимо поделить количество коробок с карамелью на количество коробок с мармеладными, то есть (3:7.)

3. Какую часть составляют мармеладные конфеты от всех конфет?

Нужно сложить количество всех коробок. Всего у нас (3 + 5 + 7 = 15) единиц отношения. Далее поделим единицы отношения мармеладных конфет на единицы отношения всех конфет. Таким образом, мармеладные конфеты по отношению ко всем конфетам составляют (7:15. )

4. Если в магазине есть 20 шоколадных конфет, то каково количество мармеладных? ​

В этом вопросе мы встречаемся с переходом от единиц отношения к абсолютной величине. Вспоминаем, что наши конфеты разложены по коробкам. То есть у нас есть 5 коробок, в которых 20 шоколадных конфет. Коробки — это единицы отношения, а шоколадные конфеты – это абсолютная величина.

Количество шоколадных конфет разделим на количество клеток (20:5 = 4), т.е. в каждой коробке 4 шоколадные конфеты.

Помним, что размер единицы отношения равен для всех элементов этого отношения. Значит, что во всех коробках в магазине находится по 4 конфеты.​

Тогда всего в магазине 28 мармеладных конфет.

Пример 2

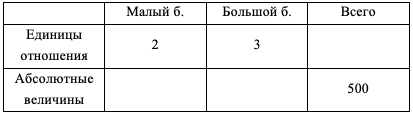
Отношение объема воды в большом и малом бассейне равно 3:2. Для того, чтобы поменять воду в этих двух бассейнах, потребуется 500 воды. Сколько воды в малом бассейне?

Решение:

Представим, что вся вода из большого бассейна хранится в 3 бочках, из малого в 2 точно таких же, это будут единицы отношения. Абсолютная величина – это весь объем бассейна.

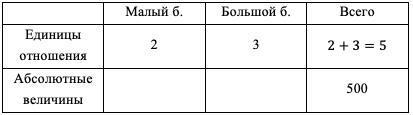
Если у нас 2 бочки от малого бассейна и 3 от большого, то всего их 5.

Мы знаем, что в 5 бочках находится 500 воды. Узнаем сколько в одной:

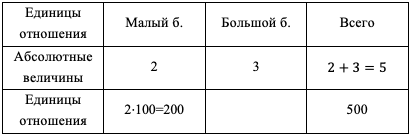
(500) : 5 = 100

Итак, узнаем, во сколько бочек вместится вся вода из малого бассейна, знаем их размерность, найдем объем малого бассейна.

Ответ: 200

Единицы отношения в геометрии

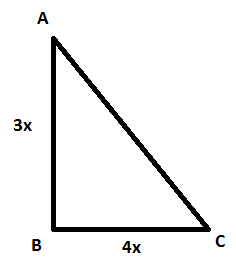
Единицы отношений могут встретиться и в задачах по геометрии. Смысл останется тем же: отношение — это какая-то сокращенная дробь. Например, может быть дано соотношение сторон или углов в задаче: стороны прямоугольного треугольника ABC AB и BC относятся как 3:4.

Так как отношение — это некая сокращенная дробь, то отношение сторон должно быть представлено следующим образом:

(frac{text{AB}}{text{BC}} = frac{3x}{4x})

То есть мы вводим переменную, чтобы показать, что отношение не является реальным значением сторон.

Стороны могут составлять 3 и 4, 6 и 8, 333 и 444 соответственно, а также принимать любые другие значения при условия сохранения данного соотношения.

Аналогичным образом можно представить углы или другие измеряемые величины.

Математика

6
класс

1.
Задачи на отношения.

            1.
Отрезок АВ разделён точкой С на отрезки АС и ВС в
отношении 2:7. Найти длину отрезка АВ, если длина отрезка
АС на 5,5 см меньше длины отрезка ВС.

            2.
С двух участков собрали урожай. Каков
урожай на каждом участке, если их отношение равно 11:14, а урожай, собранный
со второго участка, на 18 тонн больше, чем с первого?

            3.
Сплав состоит из меди и цинка. Отношение
массы меди к массе цинка равно 7:2. Найдите массу сплава, если масса
меди на 4кг больше массы цинка в сплаве.

            4.
Найти массу сплава цинка и меди, если
отношение массы меди к массе цинка в сплаве равно 3:5 и меди на 2,4г
меньше, чем цинка.

2.
Задачи на прямо пропорциональные величины.

            1.
Из 90 цветов, посаженных в цветнике,
принялись 72. На сколько процентов меньше не принявшихся цветов, чем
принявшихся?

            2.
0,8
м
ткани стоят 560 тенге. На сколько больше заплатят за 3,25 м ткани?

            3.
4
м³
зерна ржи весят 2,8 т. На сколько тонн больше весит 6,5 m³ зерна ржи?

            4.
Поезд за 4,5 часа проехал 360 км. За какое
время, двигаясь с тон же скоростью, поезд проедет расстояние, увеличенное
на 80 км?

3.
Задачи на обратно пропорциональные величины.

            1.
Все члены бригады работают в одинаковом
темпе. Четверо, рабочих успевают выполнить работу за 32ч. Сколько
времени понадобится для выполнения этой же работы трем рабочим?

            2.
Чтобы вывезти товар потребуется 21
автомашина грузоподъёмностью 2,5 т. Сколько потребовалось бы для выполнения
этой работы автомашин грузоподъёмностью 3,5 т?

            3.
15 рабочих
закончили отделку квартир в новом доме за 24 дня. За сколько дней выполнили бы
эту работу 18 рабочих?

            4.
Пешеход затратил на путь 2,5 ч, двигаясь со
скоростью 3,6 км/ч. Сколько времени затратит пешеход на тот же путь,
если его скорость будет 4,5 км/ч?

4.
Задачи на масштаб.

            1.
Комната имеет прямоугольную форму. Размеры пола этой
комнаты на плане 4см и 6см. В действительности меньшая
сторона пола 5 м. Найдите площадь комнаты н масштаб плана.

            2.
125 м
на местности соответствуют 2,5 см на плане. Найти масштаб плана и расстояние
между двумя точками на местности, если на плане оно 4,2
см.

            3.
План земельного участка квадратной формы
выполнен в масштабе 1:500. Сторона участка на плане 16см. Вычисли
площадь участка.

            4.
На карте расстояние между годами А и В равно 2,6см. а расстояние между городами
В и С – 3,7см, На местности расстояние
между- городами В и С равно 296км. Найдите расстояние на местности между годами
А и В и масштаб карты.

1 От куска материи длиной 5 м отрезали 2 м. Какую часть куска материи отрезали?
РЕШЕНИЕ

2 Длина железной дороги 360 км. Электрифицировано 240 км. Какая часть дороги электрифицирована? Во сколько раз вся дорога длиннее ее электрифицированной ?
РЕШЕНИЕ

3 Масса станка 9,6 ц, а электромотора 36 кг. Найдите отношение массы электромотора к массе станка.
РЕШЕНИЕ

722 Найдите отношение 124 к 3; 6 к 20; 12,3 к 3; 9,1 к 0,07; 0.25 к 0,55
РЕШЕНИЕ

723 Проволока разрезана на два куска. Первый кусок имеет длину 9 м, а второй 14,4 м. Найдите, какую часть всей проволоки составляет первый и второй кусок. Какую часть первый кусок составляет от длины второго
РЕШЕНИЕ

724 Внутри угла AOC проведен луч OB так, что AOB = = 56° и BOC = 40°. Какую часть угла AOC составляет AOB; BOC? Выполните построение этих углов с помощью транспортира.
РЕШЕНИЕ

725 Площадь прямоугольника 22,05 дм2. Длина 10,5 дм. Найдите отношение длины прямоугольника к его ширине. Что показывает это отношение? Запишите отношение, обратное полученному отношению. Что оно будет показывать
РЕШЕНИЕ

726 Отношение a к b равно 2/7. Найдите обратное отношение. Чему будет равно отношение m к n, если n к m 1,25?
РЕШЕНИЕ

727 Сплав из свинца и олова содержит 1,52 кг свинца и 0,76 кг олова. В каком отношении взяты свинец и олово? Какую часть сплава по массе они составляют
РЕШЕНИЕ

728 Какую часть урока заняла самостоятельная работа, которая длилась 20 мин, если продолжительность урока 45 мин?
РЕШЕНИЕ

729 В классе 36 учащихся. Из них 15 мальчиков, а остальные девочки. Какую часть учащихся составляют мальчики и девочки? Чему равно отношение их числа и что оно показывает?
РЕШЕНИЕ

730 Между двумя городами построили дорогу. Первый город построил 5/7 дороги,второй остальную часть. Во сколько раз часть дороги,построенная первым городом, больше, чем вторым?
РЕШЕНИЕ

731 Расстояние от села до города автомашина прошла за 3 ч. В первый час она прошла четверть всего расстояния, во второй — треть. Во сколько раз расстояние, пройденное в третий час, больше чем во второй? Какую часть расстояние, пройденное в первый час, составляет от пройденного в третий?
РЕШЕНИЕ

732 Молоко разлили в три бидона. В первый налили 0,1 всего молока, во второй 0,3, а в третий 0,6. Что показывает отношение 0,1 к 0,3; 0,1 к 0,6; 0,3 к 0,6; (0,3+ 0,1) к 0,6?
РЕШЕНИЕ

733 В классе 40 учащихся. 8 учащихся учатся на 5. Сколько процентов класса составляют отличники?
РЕШЕНИЕ

734 Из 250 семян погибли 10. Найдите процент всхожести
РЕШЕНИЕ

735 После установки нового оборудования завод за смену вместо 240 холодильников стал выпускать 300. На сколько процентов увеличилось производство холодильников за смену?
РЕШЕНИЕ

736 По коэффициенту трудового участия заработок между тремя рабочими распределили следующим образом: первому 40% всех денег, второму 35%, а третьему остальные 25%. Определите, округлив результаты до десятых, сколько процентов составляли деньги, полученные первым рабочим, от денег, полученных двумя другими; вторым рабочим, от денег, полученных двумя другими; первым рабочим, от денег, полученных вторым; вторым рабочим, от денег, полученных первым; третьим рабочим, от денег, полученных первым.
РЕШЕНИЕ

737 Имеющиеся деньги брат и сестра распределили так, что сестра получила в 3 раза больше, чем брат. Определите какую часть денег получила сестра и брат; сколько процентов всех денег получила сестра и брат; какую часть деньги брата составляют от денег сестры.
РЕШЕНИЕ

738 Известно, что сумма углов любого треугольника равна 180°. В треугольнике ABC найдите A, если B = 75°, C = 80°; A больше B на 20° и меньше C на 40°; B составляет 2/3, a C 1/5 суммы всех углов треугольника; A составляет 5/6 B и C = 70°
РЕШЕНИЕ

739 Что показывает отношение пути, пройденного автомашиной, ко времени ее движения; числа деталей, изготовленных станком-автоматом, ко времени его работы; стоимости купленных яблок к их массе; объема прямоугольного параллелепипеда к площади его основания?
РЕШЕНИЕ

740 Найдите, сколько процентов число 9,729 составляет от числа 84,6. С помощью микрокалькулятора для этого можно выполнить вычисление по программе 9,729 : 84,6 % =
РЕШЕНИЕ

741 Вычислите устно.
РЕШЕНИЕ

742 Найдите пропущенные числа.
РЕШЕНИЕ

743 На сколько надо увеличить знаменатель дроби 5/12, 7/17, 8/32, 2/3, чтобы получить 1/4
РЕШЕНИЕ

744 Выразите в процентах числа: 0,2; 0,15; 1/2; 3/5; 3/4; 1/20; 1; 3
РЕШЕНИЕ

745 Половина от половины числа равна половине. Найдите это число.
РЕШЕНИЕ

746 Кто быстрее? Найдите в таблице последовательно все числа от 26 до 50
РЕШЕНИЕ

747 Найдите значение выражения.
РЕШЕНИЕ

748 На подкормку овощей и фруктовых деревьев израсходовано 2/3 из имевшихся 18 ц удобрений. На подкормку овощей пошли 3/4 израсходованных удобрений. Сколько центнеров удобрений израсходовано для овощей?
РЕШЕНИЕ

749 На окраску окон и дверей было истрачено 3,2 кг белил, что составляет 5/8 всех белил, истраченных на ремонт. На него истрачено 4/5 всех купленных белил. Сколько килограммов белил куплено?
РЕШЕНИЕ

750 Найдите объем прямоугольного параллелепипеда, если его ширина 2,5 см и составляет 5/8 высоты, а длина в 3,4 раза больше высоты; его высота 3,5 см и составляет 0,7 ширины, а длина в 2,4 раза больше ширины.
РЕШЕНИЕ

751 Двое мальчиков бросали баскетбольный мяч в корзину. Один мальчик из 20 бросков имел 13 попаданий, а другой из 26 — 15 попаданий. Найдите для каждого мальчика, какую часть составляли попадания от числа бросков. Чей результат лучше?
РЕШЕНИЕ

752 Крутизной лестницы называют отношение высоты ступеньки к ее глубине. Чему равна крутизна лестницы, если высота ступеньки 18 см, а глубина 30 см?
РЕШЕНИЕ

753 Автобус в первый час прошел 30 км, во второй 24 км, а в третий 42 км. Какую часть всего пути прошел автобус в каждый час? Какую часть пути, оставшуюся после первого часа движения, он прошел во второй и в третий час
РЕШЕНИЕ

754 Для варенья на 3,6 кг ягод было взято 4,2 кг сахарного песку. В каком отношении по массе были взяты ягоды и сахарный песок?
РЕШЕНИЕ

755 В сосуд налили 240 г воды и положили 10 г соли. Найдите процентное содержание соли в растворе. Через некоторое время 50 г воды испарилось. Какое теперь стало процентное содержание соли в растворе?
РЕШЕНИЕ

756 Комбайнер намолотил 76 т зерна, превысив задание на 12 т. На сколько процентов комбайнер перевыполнил задание?
РЕШЕНИЕ

757 На складе были пшеница, овес и кукуруза, причем пшеница составляла 64%, овес 16% всего количества зерна. В товарный состав загрузили всю пшеницу и кукурузу. Какой процент погруженного зерна составляла пшеница? Какой процент составляла бы пшеница, если вместо кукурузы погрузили бы овес?
РЕШЕНИЕ

758 Длина прямоугольника a см, а ширина b см. Длина другого прямоугольника m см, а ширина n см. Найдите отношение площади первого прямоугольника к площади второго. Найдите значение получившегося выражения, если a = 9, b = 2, m = 8, n = 3; a = 6,4; b = 0,2; m = 3,2; n = 0,5
РЕШЕНИЕ

759 Найдите значение выражения.
РЕШЕНИЕ

Определение
1:

отношением двух величин называется
результат деления первой величины на вторую

Определение
2:

равенство двух отношений называется
пропорцией, а результат деления в пропорции называется коэффициентом
пропорциональности

Определение
3:

величины называются пропорциональными,
если из них можно составить пропорцию

Замечание: три величины и
более тоже могут быть пропорциональны, если из них можно составить три и
более равных отношения.

Алгоритм
решения задачи:

1)      Домножить каждый
компонент заданного отношения на  и ввести соответствующие буквенные
обозначения для пропорциональных величин, заданных в задаче;

2)      По условию
задачи составить из данных величин уравнение;

3)      Найти корень
уравнения;

4)      Найти значения
каждой из пропорциональных величин, заданных в задаче;

5)      Записать ответ
на вопрос, поставленный в задаче.

Задача 1:

При

Ответ:  кг и  кг.

Задача
2:

При

Ответ:  литров.

Задача
3:

При

Ответ:
 граммов.

1.
Для выпечки блинов требуются мука, вода и масло, взятые соответственно в
отношении . Сколько потребуется продуктов для
выпечки 3 кг 400 г блинов?

2.
Сколько вишни и сколько сахара потребуется, чтобы сварить варенье, если по
рецепту ягоды и сахар берутся в отношении , причем сахара требуется на 7 кг 600 г
больше, чем вишни?

3.
Смесь
цукатов состоит из авакадо, киви, бананов и ананасов, взятых в отношении . Найдите вес смеси, если в ней бананов
больше, чем киви на 177 грамм.