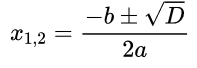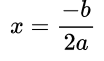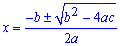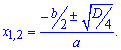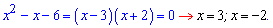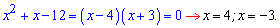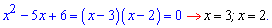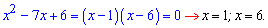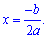Уравнение вида ax2+bx+c=0, где a,b,c – любые числа, причем a≠0, называют квадратным уравнением. Числа a,b,c принято называть коэффициентами, при этом a – первый коэффициент, b – второй коэффициент, c – свободный член.
Квадратное уравнение может иметь не более двух корней. Решить такое уравнение – это значит найти все его корни или доказать, что их нет.
Дискриминант
Количество корней квадратного уравнения зависит от такого элемента, как дискриминант (обозначают его буквой D).
Нахождение корней квадратного уравнения
Дискриминант – это такой математический инструмент, который позволяет нам определять количество корней. Он выражается определенной формулой:
D=b2–4ac
- Если D>0, то уравнение имеет два различных корня. Их находят по формуле:
- Если D<0, то уравнение не имеет корней.
- Если D=0, то уравнение имеет два равных корня, их записывают и находят как один:
Рассмотрим решение квадратных уравнений на примерах.
Пример №1. Решить уравнение х2–2х–3=0. Определяем коэффициенты: а=1, b=–2, c=–3. Находим дискриминант: D=b2–4ac=(–2)2–41(–3)=4+12=16. Видим, что дискриминант положительный, значит, уравнение имеет два различных корня, находим их:
Пример №2. Решить уравнение 5х2+2х+1=0. Определяем коэффициенты: а=5, b=2, c=1. D=b2–4ac=22–4=4–20=–16, D<0, уравнение не имеет корней.
Пример №3. Решить уравнение х2–6х+9=0. Определяем коэффициенты: а=1, b=–6, c=9.
D=b2–4ac=(–6)2–4=36–36=0, D=0, 1 корень
Теорема Виета
Приведенные квадратные уравнения
Среди квадратных уравнений встречаются такие, у которых первый коэффициент равен 1 (обратим внимание на пример 1 и 3), такие уравнения называются приведенными.
Приведенные квадратные уравнения можно решать не только с помощью дискриминанта, но и с помощью теоремы Виета.
Теорема Виета
Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком; произведение корней равно третьему коэффициенту.
х1+х2= –b
х1•х2= с
Корни с помощью данной теоремы находятся устно способом подбора. Рассмотрим это на примерах.
Пример №4. Решить уравнение х2–10х+21=0. Выпишем коэффициенты: а=1, b=–10, c=21. Применим теорему Виета:
х1+х2=–(–10)=10
х1х2=21
Начинаем с произведения корней, которое является положительным числом, значит оба корня либо отрицательные, либо положительные. Предполагаем, что это могут быть либо 3 и 7, либо противоположные им числа. Теперь смотрим на сумму, она является положительным числом, поэтому нам подходит пара чисел 3 и 7. Проверяем: 3+7=10, 37=21. Значит, корнями данного уравнения являются числа 3 и 7.
Пример №5. Решить уравнение: х2+5х+4=0. Выпишем коэффициенты: а=1, b=5, c=4. По теореме Виета:
х1+х2=–5
х1х2=4
Видим, что произведение корней равно 4, значит оба корня либо отрицательные, либо положительные. Видим, что сумма отрицательная, значит, будем брать два отрицательных числа, нам подходят –1 и –4. Проверим:
–1+(–4)=–5
(–1)(–4)=4
Ответ: –1 и –4
Задание OM2002
Решить уравнение: х2−2х+√5−х=√5−х+24
Данное уравнение является квадратным. Но в его условии присутствует квадратный корень, что усложняет нам задачу для нахождения его корней, в том плане, что необходимо увидеть, какие же ограничения на переменную х здесь будут.
Записываем обязательно в начале решения, что подкоренное выражение может быть только равным нулю или положительным числом (правило извлечения квадратного корня): ограничение на х: 5−х≥0
Решаем полученное неравенство: −х≥−5, отсюда х≤5. Следовательно, для ответа мы будем выбирать значения, которые меньше или равны 5.
Решаем наше квадратное уравнение, перенося все слагаемые из правой части в левую, изменяя при этом знаки на противоположные и приводя подобные слагаемые (выражения с квадратным корнем взаимоуничтожаются):
х2−2х+√5−х − √5−х− 24=0
Получим приведенное квадратное уравнение, корни которого можно найти подбором по теореме Виета:
х2−2х− 24=0
Итак, корнями уравнения х2−2х− 24=0 будут числа -4 и 6.
Теперь выбираем корень, обращая внимание на наше ограничение на х, т.е. корень должен быть меньше или равен 5. Таким образом, запишем, что 6 – это посторонний корень, так как 6 не≤5, а число минус 4 записываем в ответ нашего уравнения, так как −4≤5 .
Ответ: -4
pазбирался: Даниил Романович | обсудить разбор
Алла Василевская | Просмотров: 13k
Дискриминант, как и квадратные уравнения начинают изучать в курсе алгебры в 8 классе. Решить квадратное уравнение можно через дискриминант и с помощью теоремы Виета. Методика изучения квадратных уравнений, как и формулы дискриминанта достаточно неудачно прививается школьникам, как и многое в настоящем образовании. Поэтому проходят школьные годы, обучение в 9-11 классе заменяет «высшее образование» и все снова ищут — «Как решить квадратное уравнение?», «Как найти корни уравнения?», «Как найти дискриминант?» и …
Формула дискриминанта
Дискриминант D квадратного уравнения a*x^2+bx+c=0 равен D=b^2–4*a*c.
Корни (решения) квадратного уравнения зависят от знака дискриминанта (D) :
D>0 – уравнение имеет 2 различных действительных корня;
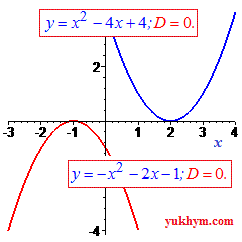
D=0 — уравнение имеет 1 корень (2 совпадающих корня):
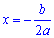
Формула для вычисления дискриминанта достаточно проста, поэтому множество сайтов предлагают онлайн калькулятор дискриминанта. Мы с такого рода скриптами еще не разобрались, поэтому кто знает, как это реализовать просим писать на почту Этот адрес электронной почты защищён от спам-ботов. У вас должен быть включен JavaScript для просмотра..
Общая формула для нахождения корней квадратного уравнения:
Корни уравнения находим по формуле
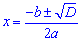
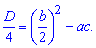
Вторая способ нахождения корней — это Теорема Виета.
Формулируется теорема не только для квадратных уравнений, но и для многочленов. Это Вы можете почитать в Википедии или других электронных ресурсах. Однако для упрощения рассмотрим ту ее часть, которая касается приведенных квадратных уравнений, то есть уравнений вида (a=1)
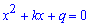
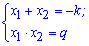
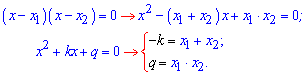
До 4 уравнения анализ должен выглядеть следующим образом. Произведение корней уравнения равно 6, следовательно корнями могут быть значения (1, 6) и (2, 3) или пары с противоположным знаком. Сумма корней равна 7 (коэффициент при переменной с противоположным знаком). Отсюда делаем вывод что решения квадратного уравнения равны x=2; x=3.
Проще подбирать корни уравнения среди делителей свободного члена, корректируя их знак с целью выполнения формул Виета. В начале это кажется трудно сделать, но с практикой на ряде квадратных уравнений такая методика окажется эффективнее вычисления дискриминанта и нахождения корней квадратного уравнения классическим способом.
Как видите школьная теория изучения дискриминанта и способов нахождения решений уравнения лишена практического смысла — «Зачем школьникам квадратное уравнение?», «Какой физический смысл дискриминанта?».
Давайте попробуем разобраться, что описывает дискриминант?
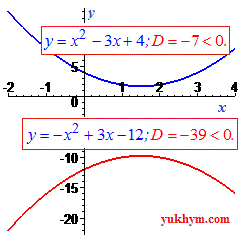
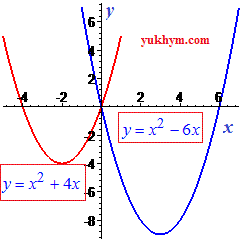
В курсе алгебры изучают функции, схемы исследования функции и построения графика функций. Из всех функций важное место занимает парабола, уравнение которой можно записать в виде
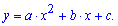
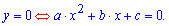
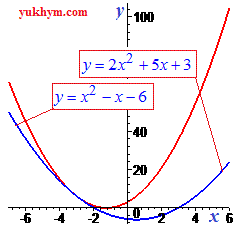
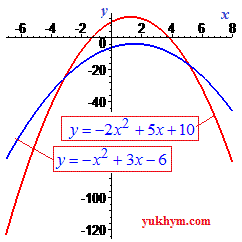
Физический смысл дискриминанта:
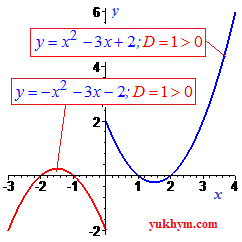
Если дискриминант больше нуля (D>0) парабола имеет две точки пересечения с осью Ox.
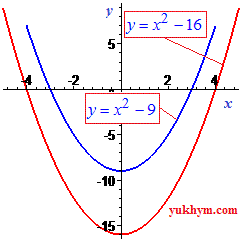
Неполные квадратные уравнения
Если в квадратном уравнении коэффициент при свободном члене или переменной равны нулю то такие уравнения называют неполными. Корни уравнений находим по упрощенной формуле
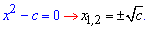
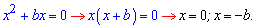
Если материал помог Вам в обучении, просьба поделиться с друзьями ссылкой на статью!
Что такое квадратные уравнения?
А теперь подробно с примерами обсудим квадратные уравнения.
Любые уравнения, сводящиеся к виду (ax^2+bx+c=0), называются квадратными. Где буквы ( b,; с) — любые числа, (aneq0). Почему (aneq0) мы обсудим ниже.
Обратите внимание на порядок слагаемых в квадратном уравнении:
(a) — всегда стоит первая и обязательно умножается на (x^2), она называется старшим коэффициентом (или первым);
(b) — принадлежит второму слагаемому и всегда умножается просто на переменную (x), это у нас второй коэффициент;
(c) — называют свободным членом, она не умножается ни на какую переменную.
В дальнейшем старайтесь приводить квадратное уравнение к виду (ax^2+bx+c=0), чтобы слагаемые стояли именно в таком порядке. Это очень важно при решении уравнений, и поможет избежать множества ошибок.
Потренируемся определять значения коэффициентов ( a, ; b,; с), чтобы запомнить порядок:
Пример 1
$$2x^2+3x+4=0;$$
$$a=2 quad b=3 quad c=4.$$
Пример 2
$$5x^2-3x-0,7=0;$$
$$a=5 quad b=-3 quad c=-0,7.$$
Пример 3
$$-x^2+2x+10=0;$$
Минус перед (x^2) можно представить в виде (-x^2=-1*x^2). Единицу обычно не пишут, поэтому минус перед первым слагаемым означает, что (a=-1):
$$a=-1 quad b=2 quad c=10.$$
Пример 4
$$3+x^2-5x=0;$$
Слагаемые стоят в неправильном порядке. Так коэффициенты находить неудобно, поэтому переставим все слагаемые в нужном порядке. От перемены мест слагаемых сумма не меняется:
$$x^2-5x+3=0;$$
$$a=1 quad b=-5 quad c=3.$$
Пример 5
$$2x^2-3x=0;$$
В уравнении нет свободного члена (c), поэтому он будет равен (0):
$$a=2 quad b=-3 quad c=0.$$
Пример 6
$$-4x^2+1=0;$$
А здесь уже нет второго коэффициента (b):
$$a=-4 quad b=0 quad c=1.$$
Уравнения, приведенные в примерах №5 и 6, называются неполными квадратными уравнениями, так как в них коэффициенты (b) или (c) равны нулю.
А вот если в уравнении коэффициенты ( a, ; b,; с) не равны 0, то такое уравнение называется полным.
От того, полное ли квадратное уравнение или неполное, зависит, как мы будем его решать. Начнем с неполных уравнений, они немного легче, но почему-то как раз в них все часто ошибаются.
Неполные квадратные уравнения
Неполное квадратное уравнение — это уравнение, в котором один из коэффициентов (b) или (c) равен нулю, (aneq0).
Как решать квадратное уравнение (ax^2+bx=0)?
Рассмотрим уравнение, в котором (c=0), оно будет иметь вид:
$$ax^2+bx=0;$$
Чтобы его решить, нужно вынести общий множитель (x) за скобки:
$$x(ax+b)=0;$$
И вспомнить правило, что произведение равно нулю, когда хотя бы один из множителей равен нулю. Здесь два множителя: (x) и ((ax+b)). Приравниваем их к нулю и решаем каждое по-отдельности:
$$x=0;$$
Тут решать-то нечего, сразу дан корень.
Второе:
$$ax+b=0;$$
Обычное линейное уравнение:
$$ax=-b;$$
$$x=frac{-b}{a};$$
Получили, что уравнение имеет сразу два корня:(x=0) и (x=frac{-b}{a}).
Разберем на примере:
Пример 7
$$2x^2+8x=0;$$
Выносим общий множитель (x):
$$x(2x+8)=0;$$
$$quad x_1=0 quad и quad 2x+8=0;$$
$$2x+8=0;$$
$$2x=-8;$$
$$x_2=-4.$$
Ответ: (x_1=0 quad и quad x_2=-4.)
Как решать квадратное уравнение (ax^2+с=0)?
Вот с такими уравнениями надо быть очень внимательными. Важно помнить, что любое число (выражение), возведенное в квадрат, всегда больше или равно нуля, оно не может быть отрицательным.
Общая схема решения уравнений вида (ax^2+с=0):
- Выражаем (x^2) из уравнения:
$$ax^2+c=0;$$
$$ax^2=-c;$$
$$x^2=frac{-c}{a};$$ -
Если (-frac{c}{a} geq 0):
$$x_1=sqrt{-frac{c}{a}};$$
$$x_2=-sqrt{-frac{c}{a}};$$ -
Если (-frac{c}{a} lt 0):
РЕШЕНИЙ НЕТ.
Пример 8
$$2x^2-8=0;$$
$$2x^2=8;$$
$$x^2=frac{8}{2};$$
$$x^2=4;$$
$$x=pmsqrt{4};$$
$$x_1=2;$$
$$x_2=-2;$$
Ответ: (x_1=2 quad и quad x_2=-2.)
Пример 9
$$4x^2+36=0;$$
$$2x^2=-36;$$
$$x^2=frac{-36}{2}=-18;$$
Так как (-18 < 0), а (x^2) не может быть отрицательным, то это уравнение не имеет корней.
Ответ: Нет корней.
Пример 10
$$frac{1}{2}x^2-frac{1}{18}=0;$$
$$frac{1}{2}x^2=frac{1}{18};$$
Чтобы избавиться от (frac{1}{2}), умножим уравнение слева и справа на (2):
$$x^2=frac{2}{18};$$
$$x^2=frac{1}{9};$$
$$x=pmsqrt{frac{1}{9}};$$
$$x_1=frac{1}{3};$$
$$x_2=-frac{1}{3};$$
Ответ: (x_1=frac{1}{3} quad и quad x_2=-frac{1}{3}.)
Решение квадратных уравнений через дискриминант
Квадратные уравнения (ax^2+bx+c=0), у которых все коэффициенты ( a, ; b,; с) не равны 0, называются полными квадратными уравнениями.
Чтобы их решать, нужно уметь находить дискриминант квадратного уравнения. Ничего страшного в этом нет, несмотря на странное называние. Дискриминантом уравнения (ax^2+bx+c=0) называют выражение:
$$D=b^2-4ac;$$
- Если дискриминант получился больше нуля ((D ge 0)), то квадратное уравнение имеет два корня, которые можно найти по формулам:
$$x_1=frac{-b+sqrt{D}}{2a};$$
$$x_2=frac{-b-sqrt{D}}{2a};$$ - Если дискриминант равен нулю ((D=0)), то квадратное уравнение имеет один корень:
$$x=frac{-b}{2a};$$ - Если дискриминант меньше нуля ((D<0)), то квадратное уравнение не имеет корней.
Примеры квадратных уравнений
Пример 11
$$2x^2-9x+4=0;$$
Прежде чем решать уравнение, я рекомендую выписать все коэффициенты:
$$a=2 quad b=-9 quad c=4.$$
Используя значения коэффициентов, можем посчитать дискриминант:
$$D=b^2-4ac=(-9)^2-4*2*4=81-32=49;$$
Ура, дискриминант посчитан и он больше нуля! Значит корней будет два, найдем их по формулам:
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-9)+sqrt{49}}{2*2}=frac{9+7}{4}=frac{16}{4}=4;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-9)—sqrt{49}}{2*2}=frac{9-7}{4}=frac{2}{4}=frac{1}{2};$$
Ответ: (x_1=4 quad и quad x_2=frac{1}{2}.)
Пример 12
$$10x^2+x-21=0;$$
$$a=10 quad b=1 quad c=-21.$$
$$D=b^2-4ac=1^2-4*10*(-21)=1+840=841;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-1+sqrt{841}}{2*10}=frac{-1+29}{20}=frac{28}{20}=frac{7}{5};$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-1-sqrt{841}}{2*10}=frac{-1-29}{20}=frac{-30}{20}=frac{-3}{2};$$
Ответ: (x_1=frac{7}{5} quad и quad x_2=-frac{3}{2}.)
Пример 13
$$(x-7)^2=2x^2+11x+23;$$
Это уравнение еще нужно привести к стандартному виду, для этого раскроем скобки по формуле «квадрат разности» ((a-b)^2=a^2-2ab+b^2):
$$x^2-14x+49=2x^2+11x+23;$$
Перекинем все слагаемые в левую часть, не забывая при этом менять знак на противоположный:
$$x^2-14x+49-2x^2-11x-23=0;$$
Приводим подобные слагаемые:
$$-x^2-25x+26=0;$$
$$a=-1 quad b=-25 quad c=26.$$
$$D=b^2-4ac=(-25)^2-4*(-1)*26=625+104=729;$$
$$x_1=frac{-b+sqrt{D}}{2a}=frac{-(-25)+sqrt{729}}{2*(-1)}=frac{25+27}{-2}=frac{52}{-2}=-26;$$
$$x_2=frac{-b-sqrt{D}}{2a}=frac{-(-25)-sqrt{729}}{2*(-1)}=frac{25-27}{-2}=frac{-2}{-2}=1;$$
Ответ: (x_1=-26 quad и quad x_2=1.)
Пример 14
$$3x^2+7x+6=0;$$
$$a=3 quad b=7 quad c=6.$$
$$D=b^2-4ac=7^2-4*3*6=49-72=-23;$$
Стоп! Дискриминант получился отрицательный, это означает, что у этого квадратного уравнения не будет корней.
Ответ: Нет корней.
Пример 15
$$4x^2-4x+1=0;$$
$$a=4 quad b=-4 quad c=1.$$
$$D=b^2-4ac=(-4)^2-4*4*1=16-16=0;$$
Дискриминат получился равен нулю. В этом случае у квадратного уравнения будет всего один корень, который можно найти по формуле:
$$x=frac{-b}{2a}=frac{-(-4)}{2*4}=frac{4}{8}=frac{1}{2};$$
Ответ: (x=frac{1}{2}.)
Полезно знать! Если дискриминант получился равен нулю, то перед вами формула полного квадрата. Это значит, что квадратный многочлен можно разложить по формуле ((apm b)^2=a^2pm 2ab+b^2).
И пример №15 можно решить, используя эту формулу:
$$4x^2-4x+1=0;$$
$$(2x-1)^2=0;$$
Квадрат равен нулю только в том случае, если выражение под квадратом равно нулю:
$$2x-1=0;$$
$$2x=1;$$
$$x=frac{1}{2};$$
Ответ получили точно такой же, как и при решении через дискриминант.
Дискриминант деленный на 4
Квадратные уравнения иногда удобно решать по упрощенной формуле дискриминанта. Но применять ее можно не во всех случаях, а только, если коэффициент (b) в уравнении (ax^2+bx+c=0) четный (делится на 2).
Итак, представим, что коэффициент (b) четный, тогда дискриминант можно посчитать по формуле:
$$D_4=left(frac{b}{2}right)^2-ac;$$
А корни уравнения находятся по формулам:
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a};$$
Кстати, обычный дискриминант (D) отличается от (D_4) в 4 раза:
$$D_4=frac{D}{4}=frac{b^2-4ac}{4}=frac{b^2}{4}-frac{4ac}{4}=left(frac{b}{2}right)^2-ac;$$
Поэтому (D_4) называют «дискриминантом деленным на 4».
Эти формулы нужны, чтобы, когда это возможно, сократить вычисления. Разберем на примере:
Пример 16
$$7x^2-20x-1067=0;$$
$$a=7 quad b=-20 quad c=-1067.$$
(b=-20) — четный, поэтому воспользуемся дискриминантом деленным на 4:
$$D_4=left(frac{b}{2}right)^2-ac=left(frac{-20}{2}right)^2-7*(-1067)=(-10)^2+7469=100+7469=7569;$$
$$x_1=frac{-frac{b}{2}+sqrt{D_4}}{a}=frac{-frac{-20}{2}+sqrt{7569}}{7}=frac{10+87}{7}=frac{97}{7};$$
$$x_2=frac{-frac{b}{2}-sqrt{D_4}}{a}=frac{-frac{-20}{2}-sqrt{7569}}{7}=frac{10-87}{7}=frac{-77}{7}=-11;$$
Ответ: (x_1=frac{97}{7} quad и quad x_2=-11.)
Возникает вопрос, зачем вообще нужен этот (D_4), если все можно считать через обычный дискриминант? Если бы мы считали пример №16 как обычно, то наш дискриминант, который и так получился не маленьким — ((D_4=7659)), был бы в четыре раза больше. А чем больше числа, тем сложнее расчеты.
Теорема Виета для решения квадратных уравнений
Теорема Виета — это еще один способ упростить решение полных квадратных уравнений. Ее очень часто используют для решения несложных квадратных уравнений в уме и для анализа квадратного многочлена, особенно это актуально в сложных заданиях с параметром в ЕГЭ.
Прежде чем сформулировать теорему Виета, познакомимся с приведенными квадратными уравнениями.
Приведенное квадратное уравнение
Квадратные уравнения (ax^2+bx+c=0), у которых коэффициент (a) при (x^2) равен (1), называют приведенными.
Например:
$$x^2+4x-3=0;$$
$$x^2-140x-65=0;$$
Любое полное квадратное уравнение всегда можно свести к приведенному. Для этого надо поделить все уравнение на коэффициент (a):
Пример 17
Привести квадратное уравнение к приведенному.
$$3x^2-15x+9=0;$$
Разделим уравнение на (a=3). (Так можно делать: если левую и правую части уравнения поделить на одно и то же число, то корни уравнения от этого не изменятся.)
$$frac{3x^2-15x+9}{3}=frac{0}{3};$$
В результате каждое слагаемое поделится на (3):
$$frac{3x^2}{3}-frac{15x}{3}+frac{9}{3}=0;$$
$$x^2-5x+3=0;$$
Формулы Виета
Сумма корней приведенного квадратного уравнения (x^2+bx+c=0) равна второму коэффициенту (b) со знаком минус, а произведение корней равно свободному члену (c).
Пусть (x_1), и (x_2) — корни квадратного уравнения (x^2+bx+c=0), тогда справедливы формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
На первый взгляд может показаться, что это очень запутанно, но на самом деле, теорема Виета часто помогает решить уравнение в уме. Попробуем на практике:
Пример 18
$$x^2+4x+3=0;$$
$$a=1 quad b=4 quad c=3.$$
Воспользуемся теоремой Виета и выпишем формулы:
$$ begin{cases}
x_1+x_2=-b; \
x_1*x_2=c. \
end{cases}$$
Подставим коэффициенты:
$$ begin{cases}
x_1+x_2=-4; \
x_1*x_2=3. \
end{cases}$$
Нужно найти такие (x_1) и (x_2), которые удовлетворяют и первому, и второму уравнениям в системе. Подобрать корни достаточно просто: рассмотрим второе уравнение, какие два числа дают при умножении (3ку)?
Либо: (3=1*3);
Либо: (3=(-1)*(-3)).
Осталось проверить, будут ли найденные множители удовлетворять первому уравнению в системе, просто подставим их:
$$1+3 neq -4;$$
$$-1+(-3) = -4;$$
Вот мы и нашли корни системы уравнений: (x_1=-1) и (x_2=-3). А самое главное, мы нашли корни исходного квадратного уравнения.
Ответ: (x_1=-1 quad и quad x_2=-3.)
Если потренироваться, то все эти вычисления можно легко проводить в уме, если коэффициенты небольшие. Главное запомнить, что произведение корней должно быть равно свободному члену (c), а сумма корней равна ((-b)).
Теорема Виета, если (aneq1)
По теореме Виета можно решать не только приведенные квадратные уравнения (у которых (a=1)). Но перед тем, как применять формулы Виета, надо привести уравнение к приведенному, поделив на первый коэффициент (a):
$$ax^2+bx+c=0; quad mid :a$$
$$frac{ax^2}{a}+frac{bx}{a}+frac{c}{a};$$
$$x^2+frac{b}{a}*x+frac{c}{a};$$
Получили приведенное квадратное уравнение, для которого можно записать формулы Виета, где вторым коэффициентом будет (frac{b}{a}), а свободным членом (frac{c}{a}):
$$ begin{cases}
x_1+x_2=-frac{b}{a}; \
x_1*x_2=frac{c}{a}. \
end{cases}$$
Пример 19
$$12x^2+x-1=0;$$
$$a=12 quad b=1 quad c=-1.$$
Коэффициент (a=12 neq 1), поэтому разделим все уравнение на (a=12):
$$12x^2+x-1=0; quad mid :12$$
$$x^2+frac{1}{12}x-frac{1}{12}=0;$$
$$a=1 quad b=frac{1}{12} quad c=-frac{1}{12}.$$
Теорема Виета:
$$ begin{cases}
x_1+x_2=-frac{1}{12}; \
x_1*x_2=-frac{1}{12}. \
end{cases}$$
Подбираем корни:
$$x_1=-frac{1}{3};$$
$$x_2=frac{1}{4};$$
Ответ: (x_1=-frac{1}{3} quad и quad x_2=frac{1}{4}.)
Теорема Виета удобна, когда у квадратного уравнения небольшие коэффициенты и можно легко подобрать корни. В остальных случаях лучше пользоваться дискриминантом.
Это уравнение вида ax2+bx+c=0ax^2 + bx + c = 0,
где aa – коэффициент перед x2x^2,
bb – коэффициент перед xx,
cc – свободное число.
Существуют разные способы нахождения корней квадратного уравнения. Пожалуй, самый основной и распространенный способ – через вычисление дискриминанта. В этом случае он рассчитывается по формуле:
D=b2–4acD = b^2 – 4ac
Если второй коэффициент уравнения четный, можно решать уравнение через kk, тогда будет другая формула дискриминанта:
D1=k2–acD_1 = k^2 – ac
Если первый коэффициент уравнения равен 1, то можно воспользоваться теоремой Виета, которая имеет 2 условия:
x1+x2=−bx_1 + x_2 = -b
x1⋅x2=cx_1 cdot x_2 = c
Но если мы захотим решить уравнение основным способом, ошибки не будет. Нахождение корней уравнения через дискриминант – универсальный способ, а остальные введены для удобства вычислений.
Задача 1
Решим уравнение: 3×2+7x−6=0.3x^2 + 7x — 6 = 0.
Обозначим коэффициенты:
a=3a = 3,
b=7b = 7,
c=−6c = -6
Далее находим дискриминант по формуле:
D=b2–4acD = b^2 – 4ac
D=72–4∗3∗(−6)=49+72=121=112D = 7^2 – 4 * 3 * (-6) = 49 + 72 = 121 = {11}^2
D>0D > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b — √D) / 2a
Подставляем численные значения:
x1=(−7+11)/2∗3=4/6=23x_1 = (-7 + 11) / 2*3 = 4 / 6 = frac{2}{3}
x2=(−7–11)/2∗3=−18/6=−3x_2 = (-7 – 11) / 2*3 = -18 / 6 = -3
Ответ: x1=23x_1 = frac{2}{3}, x2=−3x_2 = -3.
Задача 2
Решим уравнение: −x2+7x+8=0.-x^2 + 7x + 8 = 0.
Обозначим коэффициенты:
a=−1a = -1,
b=7b = 7,
c=8.c = 8.
Далее находим дискриминант по формуле:
D=b2–4acD = b^2 – 4ac
D=72–4⋅(−1)⋅8=49+32=81=92D = 7^2 – 4 cdot (-1) cdot 8 = 49 + 32 = 81 = 9^2
D>0D > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−b+√D)/2ax_1 = (-b + √D) / 2a
x2=(−b−√D)/2ax_2 = (-b — √D) / 2a
Подставляем численные значения:
x1=(−7+9)/2∗(−1)=2/(−2)=−1x_1 = (-7 + 9) / 2 * (-1) = 2 / (-2) = -1
x2=(−7–9)/2∗(−1)=−16/(−2)=8x_2 = (-7 – 9) / 2 * (-1) = -16 / (-2) = 8
Ответ: x1=−1x_1 = -1, x2=8x_2 = 8.
Задача 3
Решим уравнение: 4×2+4x+1=0.4x^2 + 4x + 1 = 0.
Обозначим коэффициенты:
a=4a = 4,
b=4b = 4,
c=1.c = 1.
Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac
D=42–4⋅4⋅1=16–16=0D = 4^2 – 4 cdot 4 cdot 1 = 16 – 16 = 0
D=0D = 0 – значит, уравнение имеет 1 корень.
Находим корень уравнения по следующей формуле: x=−b/2ax = -b / 2a
Подставляем численные значения:
x=−4/2⋅4=−4/8=−1/2=−0,5x = -4 / 2 cdot 4 = -4 / 8 = -1 / 2 = -0,5
Ответ: x=−0,5.x = -0,5.
Задача 4
Решим уравнение: 2×2+x+1=0.2x^2 + x + 1 = 0.
Обозначим коэффициенты:
a=2a = 2,
b=1b = 1,
c=1.c = 1.
Далее находим дискриминант по формуле: D=b2–4acD = b^2 – 4ac
D=12–4∗2∗1=1–8=−7D = 1^2 – 4 * 2 * 1 = 1 – 8 = -7
D<0D < 0 – значит, уравнение корней не имеет.
Ответ: корней нет.
Решение квадратного уравнения через k
Если у квадратного уравнения коэффициент bb четный, то можно решать уравнение через kk, при этом k=12bk = frac{1}{2} b.
Задача 5
Решим уравнение: −x2+2x+8=0.-x^2 + 2x + 8 = 0.
Обозначим коэффициенты:
a=−1a = -1,
b=2b = 2,
c=8c = 8
bb – четное.
k=12b=1k = frac {1}{2} b = 1.
Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac
D1=12–(−1)∗8=1+8=9=32D_1 = 1^2 – (-1) * 8 = 1 + 8 = 9 = 3^2
D1>0D_1 > 0 – значит, уравнение имеет 2 корня.
Находим корни уравнения по следующим формулам:
x1=(−k+D1)/ax_1 = (-k + {sqrt D}_1) / a
x2=(−k−D1)/ax_2 = (-k — {sqrt D}_1) / a
Подставляем численные значения:
x1=(−1+3)/(−1)=2/(−1)=−2x_1 = (-1 + 3) / (-1) = 2 / (-1) = -2
x2=(−1–3)/(−1)=−4/(−1)=4x_2 = (-1 – 3) / (-1) = -4 / (-1) = 4
Ответ: x_1 = -2, x_2 = 4.
Задача 6
Решим уравнение: 9×2–6x+1=0.9x^2 – 6x + 1 = 0.
Обозначим коэффициенты:
a=9a = 9,
b=−6b = -6,
c=1c = 1
bb – четное.
K=12b=−3.K = frac{1}{2} b = -3.
Далее находим дискриминант по формуле: D1=k2–acD_1 = k^2 – ac
D1=(−3)2–9∗1=9–9=0D_1 = {(-3)}^2 – 9 * 1 = 9 – 9 = 0
D1=0D_1 = 0 – значит, уравнение имеет 1 корень.
Находим корень уравнения по следующей формуле: x=−k/ax = -k / a
Подставляем численные значения:
x=3/9=13x = 3 / 9 = frac{1}{3}
Ответ: x=13.x = frac{1}{3}.
Нахождение корней уравнения по теореме Виета
Если в квадратном уравнении a=1a = 1, то можно найти корни уравнения по теореме Виета.
Задача 7
Найдем корни уравнения: x2+3x+2=0.x^2 + 3x + 2 = 0.
Обозначим коэффициенты:
a=1a = 1,
b=3b = 3,
c=2c = 2.
Запишем 2 условия теоремы Виета:
x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c
Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа -2 и -1.
Значит, корни уравнения равны:
x1=−2x_1 = -2
x2=−1x_2 = -1
Ответ: x1=−2x_1 = -2, x2=−1x_2 = -1.
Задача 8
Найдем корни уравнения: x2–5x+6=0.x^2 – 5x +6 = 0.
Обозначим коэффициенты:
a=1a = 1,
b=−5b = -5,
c=6c = 6
Запишем 2 условия теоремы Виета:
x1+x2=−bx_1 + x_2 = -b
x1∗x2=cx_1 * x_2 = c
Теперь методом подбора найдем 2 числа, которые будут соответствовать этим условиям. Вероятно, это числа 2 и 3.
Значит, корни уравнения равны:
x1=2x_1 = 2
x2=3x_2 = 3
Ответ: x1=2x_1 = 2, x2=3.x_2 = 3.