Если известны радиус Земли R и горизонтальный
параллакс Солнца р¤, то по формуле (3.2)
легко вычислить среднее расстояние
Земли от Солнца, т. е. значение
астрономической единицы в километрах.
Точность определения астрономической
единицы почти целиком зависит от точности
горизонтального параллакса Солнца р¤.
Однако непосредственное определение
горизонтального параллакса Солнца
способом, описанным в предыдущем
параграфе, дает слишком грубые результаты
вследствие удаленности Солнца и больших
ошибок наблюдений, возникающих от
нагревания инструмента солнечными
лучами. Поэтому точное значение
горизонтального параллакса Солнца
определяется косвенным путем, по
измеренному горизонтальному параллаксу
планеты, которая подходит к Земле на
расстояние меньшее, чем расстояние
Земли от Солнца, и наблюдение которой
удобно производить.
До XX в. для этой цели использовали
наблюдения Марса во время его великих
противостояний, когда он находится от
Земли на расстоянии около 55 млн. км.
(Противостояние планеты называется
великим, если она в это время находится
вблизи перигелия своей орбиты. Последнее
великое противостояние Марса наблюдалось
в 1971 г., следующее произойдет в 1988 г.)
Пусть для упрощения задачи в момент
великого противостояния Марса
(рис.
43) Солнце С, Земля Т и Марс М находятся
на одной прямой, причем Земля — на
среднем расстоянии а0= 1 а.е. от
Солнца, а Марс — в перигелии, на расстоянии
q = a (1 — е), где а — большая полуось и
е — эксцентриситет орбиты Марса.
Обозначим через р¤ горизонтальный
экваториальный параллакс Солнца, через
р горизонтальный экваториальный
параллакс Марса и через— его геоцентрическое расстояние (т.е.
расстояние от Земли), а через R0—
экваториальный радиус Земли. Тогда
R0
= a0
sin р¤
и
R0
=
sin p = (q — a0)
sin p = [a(l — е) — a0]:
sin p.
Приравняв правые части и заменив синусы
малых углов самими углами, получим
a0
р¤= [(1 — e) — a0]
× p,
откуда
Отношение
вычисляется с большой точностью из
теории движения планет по третьему
закону Кеплера, а параллакс Марса р и
эксцентриситет е его орбиты определяется
из наблюдений.
В 1898 г. была открыта малая планета Эрос
(или Эрот), которая в моменты своих
великих противостояний, повторяющихся
через 37 лет, иногда подходит к Земле в
2,5 раза ближе, чем Марс. Первое такое
противостояние произошло в феврале
1931 г., когда Эрос приблизился к Земле на
расстояние около 0,15 а.е. В это время его
параллакс достиг 60″. В результате
тщательных наблюдений Эроса, произведенных
на 24 обсерваториях разных стран по
заранее разработанному плану,
горизонтальный экваториальный параллакс
Солнца получился равным
р¤= 8″,790 ±
0″,001.
Самые точные определения астрономической
единицы были произведены в 1961-1963 гг. в
СССР и США по радиолокационным наблюдениям
Меркурия и Венеры. В результате этих
измерений было получено значение а.е.,
равное
149 598 500 км с ошибкой ±500 км.
р¤ = 8″,794 и 1 а.е. = 149,6 × 106 км
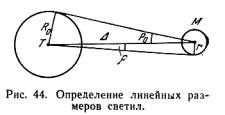
6.6. Определение размеров и формы светил
Угол, под которым с Земли виден диск
светила, называется его угловым диаметром.
Угловые диаметры некоторых небесных
тел (Солнца, Луны, планет) можно определить
непосредственно из наблюдений.
Если известен угловой диаметр (или
радиус) светила и его расстояние от
Земли, то легко вычислить его истинный
диаметр (или радиус) в линейных мерах.
Действительно, если (рис. 44) r — угловой
радиус светила М,
— расстояние между центрами светила и
Земли, р0— горизонтальный
экваториальный параллакс светила, а R0и r — линейные радиусы Земли Т и светила
М, то r =sin
,
a
R0=sin p0, откуда
или, по малости углов
и p0,
Форму небесных тел можно определить,
измеряя различные диаметры их дисков.
Если тело сплющенное, то один из его
диаметров окажется больше, а один —
меньше всех других диаметров. Измерения
диаметров планет показали, что помимо
Земли сплющенную форму имеют Марс,
Юпитер, Сатурн, Уран и Нептун.
Соседние файлы в папке Лекции
- #
- #
- #
- #
- #
- #
- #
- #
Наша компания имеет богатый опыт сотрудничества и участия в тендерах с государственными и частными компаниями. Мы предлагаем большой набор готовых решений для образовательных учреждений, а также работаем по индивидуальным техническим заданиям.
Если вы являетесь участником или организатором тендера или госзакупки, заполните, пожалуйста, форму и опишите свой запрос. Наш специалист по работе с корпоративными заказчиками обязательно с вами свяжется. Вы также можете связаться с нами по телефону: +7 (812) 418-29-44 (доб. 117 или доб. 106).
горизонтальный экваториальный параллакс Солнца, угол, под которым со среднего расстояния Солнца виден экваториальный радиус Земли. До введения в астрономическую практику радиолокационных методов определения расстояний до планет численное значение П. С. служило одной из важнейших фундаментальных астрономических постоянных, т.к. в сочетании с измеренным геодезическим путём экваториальным радиусом Земли оно определяло в км значение астрономической единицы (См. Астрономическая единица), служащей масштабом всех линейных размеров во Вселенной. Методы определения П. С. разделяются на геометрические (тригонометрические), динамические (гравитационные) и физические.
Геометрические методы определения П. С. основаны на точных астрометрических измерениях положений планет относительно звёзд. Из двух обсерваторий, лежащих почти на одном меридиане и достаточно удалённых по широте, определяют склонения той или иной планеты при помощи меридианных или вертикальных кругов (см. Астрономические инструменты и приборы); таким путём вычисляют горизонтальный экваториальный параллакс планеты. Зная периоды обращений наблюдаемой планеты и Земли, на основе 3-го закона Кеплера вычисляют и искомый П. С. Параллаксы планет можно определить и на одной обсерватории, измеряя положения планет относительно звёзд при помощи Гелиометра в различные часы суток, используя перемещение наблюдателя в пространстве вследствие суточного вращения Земли. Начиная со 2-й половины 17 в. с этой целью наблюдали Марс, приближающийся к Земле в периоды больших противостояний до 0,37 астрономической единицы (в это время параллакс Марса в 2,5 раза больше П. С.). Ещё более точными для определения П. С. являются меридианные и гелиометрические наблюдения малых планет, положения которых на небесной сфере благодаря их звездообразному виду вычисляются более надёжно. С конца 19 в. для определения П. С. используют фотографические наблюдения малых планет, приближающихся к Земле на наименьшие расстояния. Среди таких планет — Эрос, иногда сближающийся с Землёй до 1/7 астрономической единицы с параллаксом, равным 60″, а также малые планеты Икар и Географ. Следуя идеям И. Кеплера, в 18 и 19 вв. для определения П. С. наблюдали прохождения Венеры по диску Солнца (см. Прохождение планет по диску Солнца), измеряя на двух обсерваториях время, в течение которого Венера пересекает солнечный диск; теория метода разработана в 1677 Э. Галлеем (См. Галлей).
Динамические методы определения П. С. основаны на изучении возмущений в движении планет и Луны, вызываемых притяжением других небесных тел. П. С. π
π
вытекающим из 3-го закона Кеплера. П. С. вычисляется, если определена общая масса Земли и Луны, по возмущениям, вызываемым этими телами в движении какой либо планеты. Существуют и другие динамические методы определения П. С.
Физические методы определения П. С., в частности, основаны на соотношении между средней скоростью V0 движения Земли по гелиоцентрической орбите (около 29,8 км/сек) и большой полуосью а этой орбиты, т. е. в конечном счёте с П. С. Скорость V0 можно определить: измеряя лучевые скорости звёзд, лежащих вблизи эклиптики; определяя постоянную годичной аберрации χ (см. Аберрация света), равную отношению V0 к скорости света; измеряя доплеровские смещения радиолиний (с длиной волны 21 см) в спектрах межзвёздных водородных облаков. Развитие радиолокационных методов измерения расстояний между Землёй и планетами, Луной и космическими зондами, а также доплеровских смещений частот дало возможность непосредственно определить значение астрономической единицы в км. В системе астрономических постоянных, принятой в 1964, астрономическая единица равна 149,6 млн. км. Таким образом, в этой системе П. С. является производной астрономической постоянной и составляет 8,794″. При этом световая астрономическая единица (время прохождения светом расстояния, равного 1 астрономической единице) принята равной τа = 499,012 сек, а экваториальный радиус земного сфероида — равным 6378,160 км.
Лит.: Блажко С. Н., Курс сферической астрономии, 2 изд., М.— Л., 1954; Идельсон Н. И., Фундаментальные постоянные астрономии и геодезии, в кн.: Астрономический ежегодник СССР на 1942 год, М.— Л., 1941, с. 431-34; Куликов К. А., Фундаментальные постоянные астрономии, М., 1956; Фундаментальные постоянные астрономии [Материалы 21 Симпозиума Международного астрономического союза. 21 августа 1961], М., 1967; Lilley Е., Brouwer D., The solar parallax and the hydrogen line, «The Astronomical Journal», 1959, v. 64, №8.
В. К. Абалакин.
Большая советская энциклопедия. — М.: Советская энциклопедия.
1969—1978.
Параллакс Солнца
-
Параллакс Солнца, суточный параллакс Солнца (π☉) — горизонтальный экваториальный параллакс Солнца, угол, под которым со среднего расстояния Солнца виден экваториальный радиус Земли.
До 1964 года являлся фундаментальной астрономической постоянной и считался равным 8,80″. С принятием в 1964 году астрономическим союзом новой системы единиц π☉ является производной постоянной, и составляет 8,794″.Методы определения параллакса Солнца разделяются на геометрические (тригонометрические), динамические (гравитационные) и физические.
Источник: Википедия
Связанные понятия
Годичный параллакс звезды — это изменение координат звезды, вызванное изменением положения наблюдателя из-за обращения Земли вокруг Солнца. Является доказательством движения Земли вокруг Солнца и основным методом измерения расстояний до звёзд. Величина годичного параллакса данной звезды равна углу, под которым большая полуось земной орбиты видна с расстояния этой звезды. Ввиду огромных расстояний до звёзд годичные параллаксы даже у ближайших из них не превосходят одной секунды дуги.
В небесной механике механизмом, эффектом или резонансом Лидова или Лидова—Козаи называется периодическое изменение соотношения эксцентриситета и наклонения орбиты под воздействием массивного тела или тел. Либрации (колебанию около постоянного значения) подвержен аргумент перицентра.
Подробнее: Резонанс Лидова — Козаи
Сфери́ческая астроно́мия или позиционная астрономия — раздел астрономии, изучающий способы определения положения объектов на небесной сфере при наблюдении их с Земли в определённый момент времени и в определённом месте. Сферическая астрономия использует математические методы сферической геометрии и астрометрические измерения, и тесно связана с проблемой редукции наблюдений.
Общая теория относительности предсказывает множество эффектов. В первую очередь, для слабых гравитационных полей и медленно движущихся тел она воспроизводит предсказания ньютоновой теории тяготения, как это должно быть согласно принципу соответствия. Специфически отличающие её эффекты проявляются в сильных полях (например, в компактных астрофизических объектах) и/или для релятивистски движущихся тел и объектов (например, отклонение света). В случае слабых полей общая теория относительности предсказывает…
Для большинства пронумерованных астероидов известны всего несколько физических параметров. Всего несколько сотен астероидов имеют собственные страницы в Википедии, на которых содержится название, обстоятельства открытия, таблица элементов орбиты и ожидаемые физические характеристики.
Подробнее: Стандартные физические характеристики астероида
Аберра́ция све́та (лат. aberratio, от ab от и errare блуждать, уклоняться) — изменение направления распространения света (излучения) при переходе из одной системы отсчёта к другой.
Эллиптическая орбита — в астродинамике и небесной механике кеплерова орбита с эксцентриситетом меньше 1. Круговая орбита является частным случаем эллиптической орбиты при нулевом эксцентриситете. В более строгом определении эллиптической орбиты круговые орбиты исключаются; таким образом, эллиптические орбиты имеют эксцентриситет строго больше нуля и меньше единицы. В более широком смысле эллиптической орбитой является кеплерова орбита с отрицательной энергией. Такое определение включает и радиальные…
Гравитацио́нный ра́диус (или ра́диус Шва́рцшильда) представляет собой характерный радиус, определённый для любого физического тела, обладающего массой: это радиус сферы, на которой находился бы горизонт событий, создаваемый этой массой (с точки зрения ОТО), если бы она была распределена сферически-симметрично, была бы неподвижной (в частности, не вращалась, но радиальные движения допустимы), и целиком лежала бы внутри этой сферы. Введен в научный обиход немецким ученым Карлом Шварцшильдом в…
Аберра́ционное вре́мя — астрономический термин. Для вычисления орбит планет, их спутников и пр. необходимо учитывать время, за которое свет от объекта достигает наблюдателя. Это время и называют аберрационным. Определяется по уравнению: t (с) = 499,012*L, где L — расстояние до объекта в астрономических единицах.
Свето-временная коррекция определяет смещение видимого положения небесного объекта от его истинного положения (геометрического положения), вызванное движением объекта в течение времени, которое требуется свету, чтобы преодолеть расстояние от объекта до наблюдателя.
Астрономи́ческая едини́ца (русское обозначение: а.е.; международное: с 2012 года — au; ранее использовалось обозначение ua) — исторически сложившаяся единица измерения расстояний в астрономии. Исходно принималась равной большой полуоси орбиты Земли, которая в астрономии считается средним расстоянием от Земли до Солнца:126.
Динамический параллакс — метод определения параллакса и расстояния до визуально-двойной звезды, использующий сведения о массах компонентов двойной звезды, радиус орбиты и период обращения звёзд по орбите.Для определения расстояния до визуально-двойной звезды необходимо измерить угловую величину большой полуоси орбиты звезд и видимую звёздную величину. Применяя третий закон Кеплера в обобщённом виде, согласно которому произведение полной массы двойной системы и квадрата орбитального периода пропорционально…
Эпоха в астрономии (от греч. έποχή — «остановка») — момент времени, для которого определены астрономические координаты или элементы орбиты. Астрономические координаты могут быть пересчитаны из одной эпохи в другую с учётом прецессии, а также собственного движения.
Абсолютная звёздная величина — физическая величина, характеризующая светимость астрономического объекта. Для разных типов объектов используются разные определения абсолютной величины.
Орби́та (от лат. orbita «колея, дорога, путь») — траектория движения материальной точки в наперёд заданной системе пространственных координат для заданной в этих координатах конфигурации поля сил, которые на неё действуют. Термин был введён Иоганном Кеплером в книге «Новая астрономия» (1609).
Предварение равноденствий (лат. praecessio aequinoctiorum) — историческое название для постепенного смещения точек весеннего и осеннего равноденствий (то есть точек пересечения небесного экватора с эклиптикой) навстречу видимому годичному движению Солнца. Другими словами, каждый год весеннее равноденствие наступает немного раньше, чем в предыдущем году — примерно на 20 минут 24 секунды. В угловых единицах смещение составляет сейчас примерно 50,3″ в год, или 1 градус каждые 71,6 года. Это смещение…
Геодези́ческая преце́ссия (эффект де Ситтера, прецессия де Ситтера, прецессия Фоккера) — эффект изменения направления оси вращающегося тела, движущегося в искривлённом пространстве-времени, предсказанный общей теорией относительности (ОТО). Схожая модель коррекции движения системы Земля — Луна была предложена Виллемом де Ситтером в 1916 году.
Поверхностная гравитация (англ. surface gravity) — ускорение свободного падения, испытываемое на поверхности астрономического или иного объекта. Поверхностную гравитацию можно рассматривать как ускорение вследствие притяжения, испытываемое гипотетической пробной частицей, находящейся вблизи поверхности объекта и обладающей пренебрежимо малой массой, чтобы не вносить возмущения.
Эква́нт (лат. punctum aequans; от aequo «уравниваю») — понятие, используемое в древних и средневековых теориях движения планет, в частности, в геоцентрической системе мира Птолемея. Согласно этим теориям, точка, из которой движение планеты выглядит равномерным, не совпадает с геометрическим центром траектории планеты: эта точка и называется эквантом.
Функция масс двойных звёзд (англ. Binary mass function) — функция, создающая ограничения для массы ненаблюдаемого компонента (звезды или экзопланеты) в спектрально-двойных звёздах или планетных системах с одной линией. Значение определяется по наблюдаемым характеристикам: по орбитальному периоду двойной системы и пику лучевой скорости наблюдаемой звезды. Скорость одного компонента двойной и орбитальный период двойной системы предоставляют частичную информацию о расстоянии и гравитационном взаимодействии…
Планеты, обращающиеся около других звёзд, являются источниками очень слабого света в сравнении с родительской звездой, поэтому прямое наблюдение и обнаружение экзопланет является довольно сложной задачей. Помимо значительной сложности обнаружения такого слабого источника света возникает дополнительная проблема, связанная с тем, что яркость родительской звезды на много порядков превышает звёздную величину планеты, светящуюся отражённым от родительской звезды светом, и, тем самым, делает оптические…
Подробнее: Методы обнаружения экзопланет
Кривая вращения галактики — функция, описывающая кинематические свойства галактики. Может быть представлена графиком, на котором отображена зависимость орбитальной скорости звёзд и газа в галактике (ось ординат) от расстояния до центра галактики (ось абсцисс). Звёзды вращаются вокруг центра галактики с постоянной скоростью в большом диапазоне расстояний от центра галактики. Таким образом, звёзды вращаются гораздо быстрее, чем ожидалось, если бы они находились в свободном потенциале Ньютона.
Периге́лий (др.-греч. περί «пери» — вокруг, около, возле, др.-греч. ἥλιος «гелиос» — Солнце) — ближайшая к Солнцу точка орбиты планеты или иного небесного тела Солнечной системы.
Локальный стандарт покоя (ЛСП или LSR) (астрон.) — точка в пространстве, задающая начало системы координат в звёздной астрономии. Необходимость введения понятия стандарт покоя вызвана отсутствием в космосе «жёсткой» системы координат, относительно которой можно описывать движение Солнца и окружающей его группы звёзд друг относительно друга. Различают динамический и кинематический стандарт покоя.
Круговая орбита — орбита, все точки которой находятся на одинаковом расстоянии от центральной точки, создаваемая обращающимся вокруг неподвижной оси телом. Может рассматриваться как частный случай эллиптической орбиты при нулевом эксцентриситете. В Солнечной системе почти круговые орбиты у Венеры (эксцентриситет 0,0068) и Земли (эксцентриситет 0,0167).
Модифицированная ньютоновская динамика (MOND) — физическая гипотеза, альтернативная теория гравитации, предлагающая изменение в законе тяготения Ньютона, объясняющее вращение галактик без привлечения тёмной материи. Когда постоянная скорость обращения внешних частей галактик была впервые обнаружена, это было неожиданно, так как ньютоновская теория гравитации предсказывает, что чем дальше объект от центра, тем меньше его скорость. Например, для орбит планет солнечной системы скорость убывает с увеличением…
Гелиометр (от др.-греч. Ἥλιος или Ἠέλιος — солнце и métron — мера) — астрометрический инструмент для измерения небольших (до 1°) углов на небесной сфере. Название его происходит от первоначального способа применения — измерения диаметра Солнца. Позже использовался для измерения поперечников Луны, планет, планетоцентрических координат спутников планет, а также для измерения двойных звёзд и для определения параллаксов звёзд.
Ускоре́ние свобо́дного паде́ния (ускорение силы тяжести) — ускорение, придаваемое телу силой тяжести, при исключении из рассмотрения других сил.
Плоскость Лапласа — плоскость, проходящая через центр масс Солнечной системы перпендикулярно вектору момента количества движения, иначе говоря она перпендикулярна вектору суммарного орбитального момента всех планет и вращательному моменту Солнца. Названа именем первооткрывателя, французского астронома Пьера-Симона Лапласа (1749-1827), предложившего использовать её в качестве основной координатной плоскости при изучении движений тел Солнечной системы в 1789 году. В отличие от положения плоскости эклиптики…
Орбита Земли — траектория движения Земли вокруг Солнца на среднем расстоянии около 149,6 миллионов километров (152,1 млн км в афелии; 147,09 млн км в перигелии).
Оскулирующая орбита объекта в пространстве (в заданный момент времени) — гравитационная кеплерова орбита (то есть эллипс или другое сечение конуса) относительно центрального тела, которую этот объект (в соответствии с его фактическим положением и скоростью в заданный момент времени) имел бы при отсутствии в дальнейшем каких-либо возмущений (связанных с несферичностью центрального тела, гравитационным воздействием третьих тел либо силами негравитационной природы).
Сверхмасси́вная чёрная дыра́ — это чёрная дыра с массой 105—1010 масс Солнца. По состоянию на 2014 год сверхмассивные чёрные дыры обнаружены в центре многих галактик, включая Млечный Путь.
Предел Роша — радиус круговой орбиты спутника, обращающегося вокруг небесного тела, на котором приливные силы, вызванные гравитацией центрального тела, равны силам самогравитации спутника.
Уравнение времени — разница между средним солнечным временем (ССВ) и истинным солнечным временем (ИСВ), то есть УВ = ССВ — ИСВ. Эта разница в каждый конкретный момент времени одинакова для наблюдателя в любой точке Земли. Уравнение времени можно узнать из специализированных астрономических изданий, астрономических программ или вычислить по формуле, приведенной ниже.
Правило Тициуса — Бо́де (известно также как закон Бо́де) представляет собой эмпирическую формулу, приблизительно описывающую расстояния между планетами Солнечной системы и Солнцем (средние радиусы орбит). Правило было предложено И. Д. Тициусом в 1766 году и получило известность благодаря работам И. Э. Боде в 1772 году.
Время свободного падения — характерное время, которое потребуется телу для коллапса под действием силы тяготения, если никакие другие силы не противодействуют коллапсу. Играет важную роль при определении временных шкал ряда астрофизических процессов, таких как звездообразование, вспышки сверхновых звёзд.
Гиперболи́ческая траекто́рия — в астродинамике и небесной механике траектория объекта вокруг центрального тела со скоростью, достаточной для преодоления притяжения центрального тела. Форма траектории в нерелятивистском случае является гиперболой. Эксцентриситет орбиты превышает единицу.
Космологическое (метагалактическое) красное смещение — наблюдаемое для всех далёких источников (галактики, квазары) понижение частот излучения, объясняемое как динамическое удаление этих источников друг от друга и, в частности, от нашей Галактики, то есть как нестационарность (расширение) Метагалактики.
Глубинный линзированный обзор (англ. Deep Lens Survey, DLS, сокращённое от Deep Gravitational Lensing Survey — глубинный гравитационный линзированный обзор) — ультраглубокий многополосный оптический обзор из семи 4-градусных полей. При этом были использованы мозаичные ПЗС тепловизоры телескопа Бланко Национальной оптической астрономической обсерватории (обсерватория Серро-Тололо) и телескопы Майялл (Китт-Пик). Полное покрытие глубины полей потребовало 5 лет (2001—2006 годы) в четырёх диапазонах…
Параметр неопределённости U (англ. uncertainty parameter) — параметр, введённый Центром малых планет для количественного описания неопределённости вычисленной возмущённой орбиты для малой планеты. Параметр представляет собой значение в логарифмической шкале от 0 до 9, соответствующее дуге неопределённости средней аномалии малой планеты после 10 лет обращения по орбите. Параметр неопределённости также называют condition code на сайте JPL Small-Body Database Browser. Значение U не следует использовать…
Радиопульса́р — космический источник импульсного радиоизлучения, приходящего на Землю в виде периодически повторяющихся всплесков (импульсов).
Фазовый угол (англ. Phase angle) — угол между падающим на наблюдаемый объект светом и отражённым от объекта светом, получаемым наблюдателем. В рамках астрономических наблюдений обычно является углом в системе Солнце-объект-наблюдатель.
Метод движущегося скопления — в астрометрии один из методов определения расстояния до звёздного скопления. В первой половине XX века данный метод был применён к нескольким ближайшим к Солнцу скоплениям. В настоящее время для определения расстояния до скоплений применяются более точные методы.
Большая полуось — один из основных геометрических параметров объектов, образованных посредством конического сечения.
Параболическая траектория — в астродинамике и небесной механике кеплерова орбита, эксцентриситет которой равен 1. Если тело удаляется от притягивающего центра, такая орбита называется орбитой ухода, если приближается — орбитой захвата. Иногда подобную орбиту называют орбитой C3 = 0 (см. Характеристическая энергия).
Ускорение расширения Вселенной — обнаруженное в конце 1990-х годов уменьшение светимости экстремально удалённых «стандартных свечей» (сверхновых типа Ia), интерпретированное как ускорение расширения Вселенной.
Подробнее: Ускоряющаяся Вселенная
Скры́тая ма́сса — проблема противоречия между наблюдаемым поведением видимых астрономических объектов и расчётным по законам небесной механики с учётом только этих объектов.
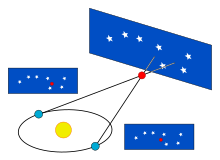
Stellar parallax motion from annual parallax. Half the apex angle is the parallax angle.
Parallax is an angle subtended by a line on a point. In the upper diagram, the Earth in its orbit sweeps the parallax angle subtended on the Sun. The lower diagram shows an equal angle swept by the Sun in a geostatic model. A similar diagram can be drawn for a star except that the angle of parallax would be minuscule.
The most important fundamental distance measurements in astronomy come from trigonometric parallax, as applied in the stellar parallax method. As the Earth orbits the Sun, the position of nearby stars will appear to shift slightly against the more distant background. These shifts are angles in an isosceles triangle, with 2 AU (the distance between the extreme positions of Earth’s orbit around the Sun) making the base leg of the triangle and the distance to the star being the long equal length legs. The amount of shift is quite small, even for the nearest stars, measuring 1 arcsecond for an object at 1 parsec’s distance (3.26 light-years), and thereafter decreasing in angular amount as the distance increases. Astronomers usually express distances in units of parsecs (parallax arcseconds); light-years are used in popular media.
Because parallax becomes smaller for a greater stellar distance, useful distances can be measured only for stars which are near enough to have a parallax larger than a few times the precision of the measurement. In the 1990s, for example, the Hipparcos mission obtained parallaxes for over a hundred thousand stars with a precision of about a milliarcsecond,[1] providing useful distances for stars out to a few hundred parsecs. The Hubble telescope WFC3 now has the potential to provide a precision of 20 to 40 microarcseconds, enabling reliable distance measurements up to 5,000 parsecs (16,000 ly) for small numbers of stars.[2][3] The Gaia space mission provided similarly accurate distances to most stars brighter than 15th magnitude.[4] Distances can be measured within 10% as far as the Galactic center, about 30,000 light years away.
Stars have a velocity relative to the Sun that causes proper motion (transverse across the sky) and radial velocity (motion toward or away from the Sun). The former is determined by plotting the changing position of the stars over many years, while the latter comes from measuring the Doppler shift of the star’s spectrum caused by motion along the line of sight. For a group of stars with the same spectral class and a similar magnitude range, a mean parallax can be derived from statistical analysis of the proper motions relative to their radial velocities. This statistical parallax method is useful for measuring the distances of bright stars beyond 50 parsecs and giant variable stars, including Cepheids and the RR Lyrae variables.[5]
Hubble precision stellar distance measurement has been extended 10 times further into the Milky Way.[7]
The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 AU per year, while for halo stars the baseline is 40 AU per year. After several decades, the baseline can be orders of magnitude greater than the Earth–Sun baseline used for traditional parallax. However, secular parallax introduces a higher level of uncertainty because the relative velocity of observed stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the uncertainty is inversely proportional to the square root of the sample size.[8]
Moving cluster parallax is a technique where the motions of individual stars in a nearby star cluster can be used to find the distance to the cluster. Only open clusters are near enough for this technique to be useful. In particular the distance obtained for the Hyades has historically been an important step in the distance ladder.
Other individual objects can have fundamental distance estimates made for them under special circumstances. If the expansion of a gas cloud, like a supernova remnant or planetary nebula, can be observed over time, then an expansion parallax distance to that cloud can be estimated. Those measurements however suffer from uncertainties in the deviation of the object from sphericity. Binary stars which are both visual and spectroscopic binaries also can have their distance estimated by similar means, and don’t suffer from the above geometric uncertainty. The common characteristic to these methods is that a measurement of angular motion is combined with a measurement of the absolute velocity (usually obtained via the Doppler effect). The distance estimate comes from computing how far the object must be to make its observed absolute velocity appear with the observed angular motion.
Expansion parallaxes in particular can give fundamental distance estimates for objects that are very far, because supernova ejecta have large expansion velocities and large sizes (compared to stars). Further, they can be observed with radio interferometers which can measure very small angular motions. These combine to provide fundamental distance estimates to supernovae in other galaxies.[9] Though valuable, such cases are quite rare, so they serve as important consistency checks on the distance ladder rather than workhorse steps by themselves.
Parsec[edit]
This section is an excerpt from Parsec.[edit]
The parsec (symbol: pc) is a unit of length used to measure the large distances to astronomical objects outside the Solar System, approximately equal to 3.26 light-years or 206,265 astronomical units (au), i.e. 30.9 trillion kilometres (19.2 trillion miles).[a] The parsec unit is obtained by the use of parallax and trigonometry, and is defined as the distance at which 1 au subtends an angle of one arcsecond[10] (1/3600 of a degree). This corresponds to 648000/π astronomical units, i.e. 1 pc = 1 au/tan(1 arcsec).[11] The nearest star, Proxima Centauri, is about 1.3 parsecs (4.2 light-years) from the Sun.[12] Most stars visible to the naked eye are within a few hundred parsecs of the Sun, with the most distant at a few thousand.[13]
The word parsec is a portmanteau of «parallax of one second» and was coined by the British astronomer Herbert Hall Turner in 1913[14] to make calculations of astronomical distances from only raw observational data easy for astronomers. Partly for this reason, it is the unit preferred in astronomy and astrophysics, though the light-year remains prominent in popular science texts and common usage. Although parsecs are used for the shorter distances within the Milky Way, multiples of parsecs are required for the larger scales in the universe, including kiloparsecs (kpc) for the more distant objects within and around the Milky Way, megaparsecs (Mpc) for mid-distance galaxies, and gigaparsecs (Gpc) for many quasars and the most distant galaxies.
In August 2015, the International Astronomical Union (IAU) passed Resolution B2 which, as part of the definition of a standardized absolute and apparent bolometric magnitude scale, mentioned an existing explicit definition of the parsec as exactly
648000/π au, or approximately 30.856775814913673×1015 metres (based on the IAU 2012 exact SI definition of the astronomical unit). This corresponds to the small-angle definition of the parsec found in many astronomical references.[15][16]
Stellar parallax[edit]
Stellar parallax created by the relative motion between the Earth and a star can be seen, in the Copernican model, as arising from the orbit of the Earth around the Sun: the star only appears to move relative to more distant objects in the sky. In a geostatic model, the movement of the star would have to be taken as real with the star oscillating across the sky with respect to the background stars.
Stellar parallax is most often measured using annual parallax, defined as the difference in position of a star as seen from the Earth and Sun, i.e. the angle subtended at a star by the mean radius of the Earth’s orbit around the Sun. The parsec (3.26 light-years) is defined as the distance for which the annual parallax is 1 arcsecond. Annual parallax is normally measured by observing the position of a star at different times of the year as the Earth moves through its orbit. Measurement of annual parallax was the first reliable way to determine the distances to the closest stars. The first successful measurements of stellar parallax were made by Friedrich Bessel in 1838 for the star 61 Cygni using a heliometer.[17] Stellar parallax remains the standard for calibrating other measurement methods. Accurate calculations of distance based on stellar parallax require a measurement of the distance from the Earth to the Sun, now based on radar reflection off the surfaces of planets.[18]
The angles involved in these calculations are very small and thus difficult to measure. The nearest star to the Sun (and thus the star with the largest parallax), Proxima Centauri, has a parallax of 0.7687 ± 0.0003 arcsec.[19] This angle is approximate that subtended by an object 2 centimeters in diameter located 5.3 kilometers away.
The fact that stellar parallax was so small that it was unobservable at the time was used as the main scientific argument against heliocentrism during the early modern age. It is clear from Euclid’s geometry that the effect would be undetectable if the stars were far enough away, but for various reasons such gigantic distances involved seemed entirely implausible: it was one of Tycho’s principal objections to Copernican heliocentrism that for it to be compatible with the lack of observable stellar parallax, there would have to be an enormous and unlikely void between the orbit of Saturn (then the most distant known planet) and the eighth sphere (the fixed stars).[21]
In 1989, the satellite Hipparcos was launched primarily for obtaining improved parallaxes and proper motions for over 100,000 nearby stars, increasing the reach of the method tenfold. Even so, Hipparcos was only able to measure parallax angles for stars up to about 1,600 light-years away, a little more than one percent of the diameter of the Milky Way Galaxy. The European Space Agency’s Gaia mission, launched in December 2013, can measure parallax angles to an accuracy of 10 microarcseconds, thus mapping nearby stars (and potentially planets) up to a distance of tens of thousands of light-years from Earth.[22][23] In April 2014, NASA astronomers reported that the Hubble Space Telescope, by using spatial scanning, can precisely measure distances up to 10,000 light-years away, a ten-fold improvement over earlier measurements.[20]
Diurnal parallax[edit]
Diurnal parallax is a parallax that varies with the rotation of the Earth or with a difference in location on the Earth. The Moon and to a smaller extent the terrestrial planets or asteroids seen from different viewing positions on the Earth (at one given moment) can appear differently placed against the background of fixed stars.[24][25]
The diurnal parallax has been used by John Flamsteed in 1672 to measure the distance to Mars at its opposition and through that to estimate the astronomical unit and the size of the Solar System.[26]
Lunar parallax[edit]
Lunar parallax (often short for lunar horizontal parallax or lunar equatorial horizontal parallax), is a special case of (diurnal) parallax: the Moon, being the nearest celestial body, has by far the largest maximum parallax of any celestial body, at times exceeding 1 degree.[27]
The diagram for stellar parallax can illustrate lunar parallax as well if the diagram is taken to be scaled right down and slightly modified. Instead of ‘near star’, read ‘Moon’, and instead of taking the circle at the bottom of the diagram to represent the size of the Earth’s orbit around the Sun, take it to be the size of the Earth’s globe, and a circle around the Earth’s surface. Then, the lunar (horizontal) parallax amounts to the difference in angular position, relative to the background of distant stars, of the Moon as seen from two different viewing positions on the Earth: one of the viewing positions is the place from which the Moon can be seen directly overhead at a given moment (that is, viewed along the vertical line in the diagram); and the other viewing position is a place from which the Moon can be seen on the horizon at the same moment (that is, viewed along one of the diagonal lines, from an Earth-surface position corresponding roughly to one of the blue dots on the modified diagram).
The lunar (horizontal) parallax can alternatively be defined as the angle subtended at the distance of the Moon by the radius of the Earth[28][29]—equal to angle p in the diagram when scaled-down and modified as mentioned above.
The lunar horizontal parallax at any time depends on the linear distance of the Moon from the Earth. The Earth-Moon linear distance varies continuously as the Moon follows its perturbed and approximately elliptical orbit around the Earth. The range of the variation in linear distance is from about 56 to 63.7 Earth radii, corresponding to a horizontal parallax of about a degree of arc, but ranging from about 61.4′ to about 54′.[27] The Astronomical Almanac and similar publications tabulate the lunar horizontal parallax and/or the linear distance of the Moon from the Earth on a periodical e.g. daily basis for the convenience of astronomers (and of celestial navigators), and the study of how this coordinate varies with time forms part of lunar theory.
Diagram of daily lunar parallax
Parallax can also be used to determine the distance to the Moon.
One way to determine the lunar parallax from one location is by using a lunar eclipse. A full shadow of the Earth on the Moon has an apparent radius of curvature equal to the difference between the apparent radii of the Earth and the Sun as seen from the Moon. This radius can be seen to be equal to 0.75 degrees, from which (with the solar apparent radius of 0.25 degrees) we get an Earth apparent radius of 1 degree. This yields for the Earth-Moon distance 60.27 Earth radii or 384,399 kilometres (238,854 mi) This procedure was first used by Aristarchus of Samos[30] and Hipparchus, and later found its way into the work of Ptolemy.[31] The diagram at the right shows how daily lunar parallax arises on the geocentric and geostatic planetary model in which the Earth is at the center of the planetary system and does not rotate. It also illustrates the important point that parallax need not be caused by any motion of the observer, contrary to some definitions of parallax that say it is, but may arise purely from motion of the observed.
Another method is to take two pictures of the Moon at the same time from two locations on Earth and compare the positions of the Moon relative to the stars. Using the orientation of the Earth, those two position measurements, and the distance between the two locations on the Earth, the distance to the Moon can be triangulated:
Example of lunar parallax: Occultation of Pleiades by the Moon
This is the method referred to by Jules Verne in From the Earth to the Moon:
Until then, many people had no idea how one could calculate the distance separating the Moon from the Earth. The circumstance was exploited to teach them that this distance was obtained by measuring the parallax of the Moon. If the word parallax appeared to amaze them, they were told that it was the angle subtended by two straight lines running from both ends of the Earth’s radius to the Moon. If they had doubts about the perfection of this method, they were immediately shown that not only did this mean distance amount to a whole two hundred thirty-four thousand three hundred and forty-seven miles (94,330 leagues) but also that the astronomers were not in error by more than seventy miles (≈ 30 leagues).
Solar parallax[edit]
After Copernicus proposed his heliocentric system, with the Earth in revolution around the Sun, it was possible to build a model of the whole Solar System without scale. To ascertain the scale, it is necessary only to measure one distance within the Solar System, e.g., the mean distance from the Earth to the Sun (now called an astronomical unit, or AU). When found by triangulation, this is referred to as the solar parallax, the difference in position of the Sun as seen from the Earth’s center and a point one Earth radius away, i.e., the angle subtended at the Sun by the Earth’s mean radius. Knowing the solar parallax and the mean Earth radius allows one to calculate the AU, the first, small step on the long road of establishing the size and expansion age[32] of the visible Universe.
A primitive way to determine the distance to the Sun in terms of the distance to the Moon was already proposed by Aristarchus of Samos in his book On the Sizes and Distances of the Sun and Moon. He noted that the Sun, Moon, and Earth form a right triangle (with the right angle at the Moon) at the moment of first or last quarter moon. He then estimated that the Moon–Earth–Sun angle was 87°. Using correct geometry but inaccurate observational data, Aristarchus concluded that the Sun was slightly less than 20 times farther away than the Moon. The true value of this angle is close to 89° 50′, and the Sun is about 390 times farther away.[30] He pointed out that the Moon and Sun have nearly equal apparent angular sizes and therefore their diameters must be in proportion to their distances from Earth. He thus concluded that the Sun was around 20 times larger than the Moon; this conclusion, although incorrect, follows logically from his incorrect data. It does suggest that the Sun is larger than the Earth, which could be taken to support the heliocentric model.[33]
Measuring Venus transit times to determine solar parallax
Although Aristarchus’ results were incorrect due to observational errors, they were based on correct geometric principles of parallax, and became the basis for estimates of the size of the Solar System for almost 2000 years, until the transit of Venus was correctly observed in 1761 and 1769.[30] This method was proposed by Edmond Halley in 1716, although he did not live to see the results. The use of Venus transits was less successful than had been hoped due to the black drop effect, but the resulting estimate, 153 million kilometers, is just 2% above the currently accepted value, 149.6 million kilometers.
Much later, the Solar System was «scaled» using the parallax of asteroids, some of which, such as Eros, pass much closer to Earth than Venus. In a favorable opposition, Eros can approach the Earth to within 22 million kilometers.[34] During the opposition of 1900–1901, a worldwide program was launched to make parallax measurements of Eros to determine the solar parallax (or distance to the Sun), with the results published in 1910 by Arthur Hinks of Cambridge[35] and Charles D. Perrine of the Lick Observatory, University of California.[36] Perrine published progress reports in 1906[37] and 1908.[38] He took 965 photographs with the Crossley Reflector and selected 525 for measurement.[39] A similar program was then carried out, during a closer approach, in 1930–1931 by Harold Spencer Jones.[40] The value of the Astronomical Unit (roughly the Earth-Sun distance) obtained by this program was considered definitive until 1968, when radar and dynamical parallax methods started producing more precise measurements.
Also radar reflections, both off Venus (1958) and off asteroids, like Icarus, have been used for solar parallax determination. Today, use of spacecraft telemetry links has solved this old problem. The currently accepted value of solar parallax is 8.794143 arcseconds.[41]
Moving-cluster parallax[edit]
The open stellar cluster Hyades in Taurus extends over such a large part of the sky, 20 degrees, that the proper motions as derived from astrometry appear to converge with some precision to a perspective point north of Orion. Combining the observed apparent (angular) proper motion in seconds of arc with the also observed true (absolute) receding motion as witnessed by the Doppler redshift of the stellar spectral lines, allows estimation of the distance to the cluster (151 light-years) and its member stars in much the same way as using annual parallax.[42]
Dynamical parallax[edit]
Dynamical parallax has sometimes also been used to determine the distance to a supernova when the optical wavefront of the outburst is seen to propagate through the surrounding dust clouds at an apparent angular velocity, while its true propagation velocity is known to be the speed of light.[43]
Spatio-temporal parallax[edit]
From enhanced relativistic positioning systems, spatio-temporal parallax generalizing the usual notion of parallax in space only has been developed. Then, event fields in spacetime can be deduced directly without intermediate models of light bending by massive bodies such as the one used in the PPN formalism for instance.[44]
Statistical parallax[edit]
Two related techniques can determine the mean distances of stars by modelling the motions of stars. Both are referred to as statistical parallaxes, or individually called secular parallaxes and classical statistical parallaxes.
The motion of the Sun through space provides a longer baseline that will increase the accuracy of parallax measurements, known as secular parallax. For stars in the Milky Way disk, this corresponds to a mean baseline of 4 AU per year, whereas for halo stars the baseline is 40 AU per year. After several decades, the baseline can be orders of magnitude greater than the Earth–Sun baseline used for traditional parallax. However, secular parallax introduces a higher level of uncertainty because the relative velocity of other stars is an additional unknown. When applied to samples of multiple stars, the uncertainty can be reduced; the precision is inversely proportional to the square root of the sample size.[45]
The mean parallaxes and distances of a large group of stars can be estimated from their radial velocities and proper motions. This is known as a classical statistical parallax. The motions of the stars are modelled to statistically reproduce the velocity dispersion based on their distance.[45][46]
Other methods for distance measurement in astronomy[edit]
In astronomy, the term «parallax» has come to mean a method of estimating distances, not necessarily utilizing a true parallax, such as:
- Photometric parallax method
- Spectroscopic parallax
- Dynamical parallax
See also[edit]
- Cosmic distance ladder
- Lunar distance (astronomy)
Notes[edit]
- ^ One trillion here is short scale, ie. 1012 (one million million, or billion in long scale).
References[edit]
- ^
Perryman, M. A. C.; et al. (1999). «The HIPPARCOS Catalogue». Astronomy and Astrophysics. 323: L49–L52. Bibcode:1997A&A…323L..49P. - ^ Harrington, J. D.; Villard, R. (10 April 2014). «NASA’s Hubble Extends Stellar Tape Measure 10 Times Farther Into Space». NASA. Archived from the original on 17 February 2019. Retrieved 17 October 2014.
- ^
Riess, A. G.; Casertano, S.; Anderson, J.; MacKenty, J.; Filippenko, A. V. (2014). «Parallax Beyond a Kiloparsec from Spatially Scanning the Wide Field Camera 3 on the Hubble Space Telescope». The Astrophysical Journal. 785 (2): 161. arXiv:1401.0484. Bibcode:2014ApJ…785..161R. doi:10.1088/0004-637X/785/2/161. S2CID 55928992. - ^ Brown, A. G. A.; et al. (Gaia collaboration) (August 2018). «Gaia Data Release 2: Summary of the contents and survey properties». Astronomy & Astrophysics. 616. A1. arXiv:1804.09365. Bibcode:2018A&A…616A…1G. doi:10.1051/0004-6361/201833051.
- ^
B., Baidyanath (2003). An Introduction to Astrophysics. PHI Learning Private Limited. ISBN 978-81-203-1121-3. - ^ «Hubble finds Universe may be expanding faster than expected». Archived from the original on 11 September 2018. Retrieved 3 June 2016.
- ^ «Hubble stretches the stellar tape measure ten times further». ESA/Hubble Images. Archived from the original on October 30, 2017. Retrieved April 12, 2014.
- ^
Popowski, P.; Gould, A. (1998). «Mathematics of Statistical Parallax and the Local Distance Scale». arXiv:astro-ph/9703140. - ^
Bartel, N.; et al. (1994). «The shape, expansion rate and distance of supernova 1993J from VLBI measurements». Nature. 368 (6472): 610–613. Bibcode:1994Natur.368..610B. doi:10.1038/368610a0. S2CID 4316734. - ^ «Cosmic Distance Scales – The Milky Way». Retrieved 24 September 2014.
- ^ B. Luque; F. J. Ballesteros (2019). «To the Sun and beyond». Nature Physics. 15 (12): 1302. Bibcode:2019NatPh..15.1302L. doi:10.1038/s41567-019-0685-3.
- ^ Benedict, G. F.; et al. «Astrometric Stability and Precision of Fine Guidance Sensor #3: The Parallax and Proper Motion of Proxima Centauri» (PDF). Proceedings of the HST Calibration Workshop. pp. 380–384. Retrieved 11 July 2007.
- ^ «Farthest Stars». StarDate. University of Texas at Austin. 15 May 2021. Retrieved 5 September 2021.
- ^ Dyson, F. W. (March 1913). «The distribution in space of the stars in Carrington’s Circumpolar Catalogue». Monthly Notices of the Royal Astronomical Society. 73 (5): 342. Bibcode:1913MNRAS..73..334D. doi:10.1093/mnras/73.5.334.
[paragraph 14, page 342] Taking the unit of distance R* to be that corresponding to a parallax of 1″·0 [… Footnote:]
* There is need for a name for this unit of distance. Mr. Charlier has suggested Siriometer, but if the violence to the Greek language can be overlooked, the word Astron might be adopted. Professor Turner suggests Parsec, which may be taken as an abbreviated form of «a distance corresponding to a parallax of one second». - ^ Cox, Arthur N., ed. (2000). Allen’s Astrophysical Quantities (4th ed.). New York: AIP Press / Springer. Bibcode:2000asqu.book…..C. ISBN 978-0387987460.
- ^ Binney, James; Tremaine, Scott (2008). Galactic Dynamics (2nd ed.). Princeton, NJ: Princeton University Press. Bibcode:2008gady.book…..B. ISBN 978-0-691-13026-2.
- ^ Zeilik & Gregory 1998, p. 44.
- ^ Zeilik & Gregory 1998, § 22-3.
- ^ Benedict, G. Fritz, et al. (1999). «Interferometric Astrometry of Proxima Centauri and Barnard’s Star Using Hubble Space Telescope Fine Guidance Sensor 3: Detection Limits for Substellar Companions». The Astronomical Journal. 118 (2): 1086–1100. arXiv:Astro-ph/9905318. Bibcode:1999AJ….118.1086B. doi:10.1086/300975. S2CID 18099356.
- ^ a b Harrington, J.D.; Villard, Ray (10 April 2014). «NASA’s Hubble Extends Stellar Tape Measure 10 Times Farther Into Space». NASA. Archived from the original on 12 April 2014. Retrieved 11 April 2014.
- ^ Dobrzycki, J. (1973). Dobrzycki, Jerzy (ed.). The Reception of Copernicus’ Heliocentric Theory. p. 51. doi:10.1007/978-94-015-7614-7. ISBN 978-90-481-8340-1.
- ^ «Soyuz ST-B successfully launches Gaia space observatory». nasaspaceflight.com. 19 December 2013. Archived from the original on 19 December 2013. Retrieved 19 December 2013.
- ^ Henney, Paul J. «ESA’s Gaia Mission to study stars». Astronomy Today. Archived from the original on 2008-03-17. Retrieved 2008-03-08.
- ^ Seidelmann, P. Kenneth (2005). Explanatory Supplement to the Astronomical Almanac. University Science Books. pp. 123–125. ISBN 978-1-891389-45-0.
- ^ Barbieri, Cesare (2007). Fundamentals of astronomy. CRC Press. pp. 132–135. ISBN 978-0-7503-0886-1.
- ^ Van Helden, A. (2010). Measuring the universe: cosmic dimensions from Aristarchus to Halley. University of Chicago Press. Ch. 12.
- ^ a b «D». The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981.
- ^ The Astronomical Almanac. [Department of Defense] Navy Department, Naval Observatory, Nautical Almanac Office. 1981. p. M10.
- ^ United States Naval Observatory. Nautical Almanac Office; Great Britain. Nautical Almanac Office (2006). Explanatory Supplement to the Astronomical Almanac. University Science Books. p. 125. ISBN 978-1-891389-45-0.
- ^ a b c Gutzwiller, Martin C. (1998). «Moon–Earth–Sun: The oldest three-body problem». Reviews of Modern Physics. 70 (2): 589–639. Bibcode:1998RvMP…70..589G. doi:10.1103/RevModPhys.70.589.
- ^ Webb, Stephen (1999), «3.2 Aristarchus, Hipparchus, and Ptolemy», Measuring the Universe: The Cosmological Distance Ladder, Springer, pp. 27–35, ISBN 9781852331061. See in particular p. 33: «Almost everything we know about Hipparchus comes down to us by way of Ptolemy.»
- ^ Freedman, W.L. (2000). «The Hubble constant and the expansion age of the Universe». Physics Reports. 333 (1): 13–31. arXiv:astro-ph/9909076. Bibcode:2000PhR…333…13F. doi:10.1016/S0370-1573(00)00013-2. S2CID 413222.
- ^ Al-Khalili, Jim (2010), Pathfinders: The Golden Age of Arabic Science, Penguin UK, p. 270, ISBN 9780141965017, archived from the original on 2015-03-17,
Some have suggested that his calculation of the relative size of the earth and sun led Aristarchus to conclude that it made more sense for the earth to be moving around the much larger sun than the other way round.
- ^ Whipple 2007, p. 47.
- ^ Hinks, Arthur R. (1909). «Solar Parallax Papers No. 7: The General Solution from the Photographic Right Ascensions of Eros, at the Opposition of 1900». Monthly Notices of the Royal Astronomical Society. 69 (7): 544–67. Bibcode:1909MNRAS..69..544H. doi:10.1093/mnras/69.7.544.
- ^ Perrine, Charles D. (1910). Determination of the solar parallax from photographs of Eros made with the Crossley reflector of the Lick Observatory University of California (First ed.). Washington, D. C.: Carnegie Institution of Washington. pp. 1–104.
- ^ Perrine, C. D. (1906). «The Measurement and Reduction of the Photographs of Eros Made With the Crossley Reflector in 1900». Publications of the Astronomical Society of the Pacific. 18 (10): 226.
- ^ Perrine, Charles D. (1908). «Progress on the Crossley Eros Solar Parallax Work». Publications of the Astronomical Society of the Pacific. 20 (120): 184. Bibcode:1908PASP…20..184P. doi:10.1086/121816. S2CID 121782316.
- ^ Campbell, W. W. (1906). «Reports of the Observatories: Lick Observatory». Publications of the Astronomical Society of the Pacific. 19 (113): 92.
- ^ Jones, H. Spencer (1941). «The Solar Parallax and the Mass of the Moon from Observations of Eros at the Opposition of 1931». Mem. Roy. Astron. Soc. 66: 11–66.
- ^ «Astronomical Constants» (PDF). US Naval Observatory. Archived from the original (PDF) on 2011-07-20.
- ^ Vijay K. Narayanan; Andrew Gould (1999). «A Precision Test of Hipparcos Systematics toward the Hyades». The Astrophysical Journal. 515 (1): 256. arXiv:astro-ph/9808284. Bibcode:1999ApJ…515..256N. doi:10.1086/307021. S2CID 15351552.
- ^ Panagia, N.; Gilmozzi, R.; MacChetto, F.; Adorf, H.-M.; et al. (1991). «Properties of the SN 1987A circumstellar ring and the distance to the Large Magellanic Cloud». The Astrophysical Journal. 380: L23. Bibcode:1991ApJ…380L..23P. doi:10.1086/186164.
- ^ Rubin, J.L. (2015). «Relativistic Pentametric Coordinates from Relativistic Localizing Systems and the Projective Geometry of the Spacetime Manifold». Electronic Journal of Theoretical Physics. 12 (32): 83–112. Archived from the original on 2015-02-08.
- ^ a b Popowski, Piotr; Gould, Andrew (29 January 1998). «Mathematics of Statistical Parallax and the Local Distance Scale». arXiv:astro-ph/9703140. Bibcode:1997astro.ph..3140P.
- ^ Layden, Andrew C; Hanson, Robert B; Hawley, Suzanne L; Klemola, Arnold R; Hanley, Christopher J (1996). «The Absolute Magnitude and Kinematics of RR Lyrae Stars Via Statistical Parallax». The Astronomical Journal. 112: 2110. arXiv:astro-ph/9608108. Bibcode:1996AJ….112.2110L. doi:10.1086/118167. S2CID 8732647.