Основные понятия
Теорема Пифагора, определение: в прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Гипотенуза — сторона, лежащая напротив прямого угла.
Катет — одна из двух сторон, образующих прямой угол.
Формула Теоремы Пифагора выглядит так:
a2 + b2 = c2,
где a, b — катеты, с — гипотенуза.
Из этой формулы можно вывести следующее:
- a = √c2 − b2
- b = √c2 − a2
- c = √a2 + b2
Запоминаем
в любом прямоугольном треугольнике сумма квадратов длин двух катетов равна квадрату длины гипотенузы.
Для треугольника со сторонами a, b и c, где c — большая сторона, действуют следующие правила:
- если c2 < a2 + b2, значит угол, противолежащий стороне c, является острым.
- если c2 = a2 + b2, значит угол, противолежащий стороне c, является прямым.
- если c2 > a2 +b2, значит угол, противолежащий стороне c, является тупым.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Теорема Пифагора: доказательство
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Дано: ∆ABC, в котором ∠C = 90º.
Доказать: a2 + b2 = c2.
Пошаговое доказательство:
- Проведём высоту из вершины C на гипотенузу AB, основание обозначим буквой H.
- Прямоугольная фигура ∆ACH подобна ∆ABC по двум углам:
∠ACB =∠CHA = 90º,
∠A — общий.
- Также прямоугольная фигура ∆CBH подобна ∆ABC:
∠ACB =∠CHB = 90º,
∠B — общий.
- Введем новые обозначения: BC = a, AC = b, AB = c.
- Из подобия треугольников получим: a : c = HB : a, b : c = AH : b.
- Значит a2 = c * HB, b2 = c * AH.
- Сложим полученные равенства:
a2 + b2 = c * HB + c * AH
a2 + b2 = c * (HB + AH)
a2 + b2 = c * AB
a2 + b2 = c * c
a2 + b2 = c2
Теорема доказана.
Обратная теорема Пифагора: доказательство
Если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник является прямоугольным.
Дано: ∆ABC
Доказать: ∠C = 90º
Пошаговое доказательство:
- Построим прямой угол с вершиной в точке C₁.
- Отложим на его сторонах отрезки C₁A₁ = CA и C₁B₁ = CB.
- Проведём отрезок A₁B₁.
- Получилась фигура ∆A₁B₁C₁, в которой ∠C₁=90º.
- В этой фигуре ∆A₁B₁C₁ применим теорему Пифагора: A₁B₁2 = A₁C₁2 + B₁C₁2.
- Таким образом получится:
- Значит, в фигурах треугольниках ∆ABC и ∆A₁B₁C₁:
- C₁A₁ = CA и C₁B₁ = CB по результату построения,
- A₁B₁ = AB по доказанному результату.
- Поэтому, ∆A₁B₁C₁ = ∆ABC по трем сторонам.
- Из равенства фигур следует равенство их углов: ∠C =∠C₁ = 90º.
Обратная теорема доказана.
Решение задач
Задание 1. Дан прямоугольный треугольник ABC. Его катеты равны 6 см и 8 см. Какое значение у гипотенузы?
Как решаем:
-
Пусть катеты a = 6 и b = 8.
-
По теореме Пифагора c2 = a2 + b2.
-
Подставим значения a и b в формулу:
c2 = 62 + 82 = 36 + 64 = 100
c = √100 = 10.
Ответ: 10.
Задание 2. Является ли треугольник со сторонами 8 см, 9 см и 11 см прямоугольным?
Как решаем:
- Выберем наибольшую сторону и проверим, выполняется ли теорема Пифагора:
112 = 82 + 92
121 ≠ 145
Ответ: треугольник не является прямоугольным.
План урока:
Теорема Пифагора
Задачи на применение теоремы Пифагора
Пифагоровы тройки
Обратная теорема Пифагора
Формула Герона
Теорема Пифагора
Попытаемся установить связь между гипотенузой и катетами прямоугольного треугольника. Пусть в некотором прямоугольном треуг-ке катеты имеют длины а и b, а гипотенуза равна с. Пусть один из острых углов треуг-ка составляет α, тогда другой острый угол должен равняться 90 – α:
Далее возьмем 4 таких треуг-ка и расположим их следующим образом:
Здесь мы прикладываем треуг-ки так, чтобы их разные катеты образовали одну сторону четырехугольника. В результате получается большой квадрат со стороной a + b. Квадратом он является по определению, ведь все его стороны одинаковы, а углы – прямые.
Изучим центральную фигуру, чью площадь мы обозначили как S2. Это четырехуг-к, причем все его стороны равны с, то есть длине гипотенузы треугольника. С другой стороны, каждый его угол можно найти, вычтя из 180° величины α и 90° – α:
Получается, что всего его углы прямые, то есть он является квадратом. Найдем его площадь:
Вернемся к большому квадрату. С одной стороны, его площадь можно записать как сумму площадей фигур, его составляющих:
Cдругой стороны, эту же площадь можно найти, просто возведя в квадрат его сторону:
Получили формулу, в которой и заключен смысл теоремы Пифагора:
Изучим несколько простейших примеров использования теоремы Пифагора.
Задание. Длины катетов прямоугольного треугольника составляют 5 и 12. Определите длину гипотенузы.
Решение. Запишем теорему Пифагора:
Задание. Длина катета треугольника составляет 3, а гипотенузы – 5. Какова длина другого катета?
Решение: На это раз нам известен один из катетов а = 3 и гипотенуза с = 5. Подставим в теорему Пифагора эти числа:
Теорема Пифагора имеет огромное значение для геометрии и смежных дисциплин. Приведенное здесь ее доказательство является одним из простейших, но отнюдь не единственным. Сегодня человечеству известно 367 различных доказательств теоремы Пифагора, что лишь показывает ее огромную значимость.
На самом деле Пифагор, известный древнегреческий математик, не был первым, кто обнаружил это равенство. Пифагор родился примерно в 570 г. до н. э., однако ещё египтяне знали про прямоугольный треуг-к со сторонами 3, 4 и 5. Поэтому его часто именуют египетским треугольником.
Также вычислять стороны прямоугольного треуг-ка умели и в Вавилоне уже за 1000 лет до рождения Пифагора. Вероятно, Пифагор узнал о формуле от вавилонян, а сам лишь вывел ее доказательство (вавилоняне не утруждали себя необходимостью доказывать теоремы геометрии). Утверждается, что Пифагор принес сделал жертвоприношение в размере 100 быков после того, как смог доказать теорему.
Задание. Вычислите гипотенузу равнобедренного прямоугольного треуг-ка, чьи катеты имеют единичную длину.
Решение. В теорему Пифагора вместо букв a и b подставим единицу:
Обратите внимание, что в данной задаче в качестве длины гипотенузы прямоугольного треугольника получилось иррациональное число. Исторически именно при решении подобной задачи люди (это были ученики Пифагора) впервые столкнулись с иррациональными числами. Перед дальнейшим изучением темы есть смысл вспомнить основные правила вычислений с квадратными корнями.
Задание. На рисунке построен произвольный квадрат. Предложите способ, как построить квадрат с вдвое большей площадью.
Решение. Проведем в исходном квадрате диагональ. Далее построим новый квадрат со стороной, равной этой гипотенузе:
Докажем, что получившийся квадрат (его стороны отмечены синим цветом) вдвое больше исходного квадрата. Пусть сторона изначального квадрата равна х.Тогда его площадь составляет х2. Диагональ разбивает квадрат на два прямоугольных треуг-ка, в которых она является гипотенузой.
Запишем для одного из них теорему Пифагора:
Но площадь квадрата равна его стороне, возведенной во вторую степень, поэтому величина с2– это площадь большого (на рисунке – синего)квадрата, а х2 – площадь маленького:
Подставим эти выражения в формулу, выведенную из теоремы Пифагора, и получим, что площадь большего квадрата ровно вдвое больше:
Задание. Найдите площадь равнобедренного прямоугольного треуг-ка, гипотенуза которого имеет длину 10.
Решение. Обозначим катеты переменной х, тогда теорема Пифагора будет выглядеть как уравнение:
Задание. Один из острых углов прямоугольного треугольника составляет 30°, а его гипотенуза равна 10. Найдите оба катета.
Решение. Мы знаем, что в прямоугольном треуг-ке с острым углом 30° гипотенуза вдвое длиннее меньшего катета (он как раз лежит против угла 30°), мы можем найти этот катет:
10:2 = 5
Другой катет находим с помощью теоремы Пифагора:
Задачи на применение теоремы Пифагора
Теорема Пифагора используется в огромном количестве геометрических задач. С ее помощью можно находить диагонали некоторых четырехуг-ков, длины высот, вычислять площади.
Задание. Стороны прямоуг-ка имеют длину 8 и 15 см. Найдите длину его диагонали.
Решение. Рассмотрим произвольный прямоугольник АВСD. Если в нем провести диагональ ВD, то получится прямоугольный треуг-к АВD. Пусть АВ = 15, АD = 8. Запишем теорему Пифагора для ∆АВD:
Задание. В равнобедренном треуг-ке основание имеет длину 16 см, а боковые стороны составляют 17 см. Найдите длину высоты, проведенной к основанию этого треуг-ка, а также площадь треуг-ка.
Решение. Напомним, что высота, опущенная к основанию равнобедренного треуг-ка, одновременно является и медианой, и биссектрисой. Это значит, что Н – середина АВ. Тогда можно найти длину отрезков АН и НВ:
Теперь можно рассмотреть ∆АСН. Он прямоугольный, и нам известно его гипотенуза (она является боковой стороной ∆АВС и по условию равна 17 см) и катет АН. Тогда можно найти и второй катет, то есть высоту СН:
Задание. Высота равностороннего треуг-ка составляет 4 см. Найдите его сторону.
Решение. Напомним, что в равностороннем треуг-ке все углы равны 60°. Также учтем, что высота в равностороннем треуг-ке является также и биссектрисой и медианой:
Рассмотрим ∆АСН. Он прямоугольный, и один из его углов составляет 60°. Значит, другой угол составляет 30°. Но в таком треуг-ке гипотенуза вдвое больше катета, лежащего против ∠30°:
Обратите внимание, мы специально домножили дробь на корень из 3, чтобы корень оказался в числителе, а не знаменателе. Т.к. в таком виде проще работать с квадратными корнями.
Итак, мы нашли АН. Теперь можно найти сторону АС, которая вдвое длиннее:
Задание. Составьте формулу для нахождения площади равностороннего треуг-ка, если известна только его сторона.
Решение. Обозначим сторону треуг-ка буквой а. Для вычисления площади необходимо найти высоту:
Как и в предыдущей задаче, отрезок АС вдвое длиннее АН:
Высоту мы нашли. Осталось найти площадь:
Задание. В прямоугольном треуг-ке, катеты которого имеют длину 60 и 80, проведена высота к гипотенузе. Найдите высоту гипотенузы, а также длину отрезков, на которые эта высота разбивает гипотенузу.
Решение. Найдем длину гипотенузы ВС:
Осталось найти длины отрезков СН и НВ. Для этого необходимо записать теорему Пифагора для ∆АСН и ∆АНВ, которые являются прямоугольными. Начнем с ∆АСН:
Аналогично работаем и с ∆АНВ:
Можно проверить себя. Отрезки НВ и СН вместе составляют отрезок СВ, поэтому должно выполняться равенство:
Задание. Диагонали ромба равны 10 и 24 см. Чему равна его сторона?
Пусть в ромбе АВСD диагонали пересекаются в точке О, причем АС = 24 см, а ВD = 10 см.Напомним, что диагонали ромба пересекаются под углом 90° и делятся при этом на одинаковые отрезки. Следовательно, ∆АВО прямоугольный. Найдем его катеты:
Задание. Основания равнобедренной трапеции имеют длину 20 и 10, а боковая сторона имеет длину 13. Найдите площадь трапеции.
Решение. Опустим на большее основание две высоты:
В итоге получили прямоуг-к АВКН. Его противоположные стороны одинаковы, поэтому
∆АНD и ∆ВКС равны друг другу, ведь это прямоугольные треуг-ки с одинаковой гипотенузой (АD = ВС, ведь это равнобедренная трапеция) и равным катетом (АН = ВК как стороны прямоуг-ка). Это значит, что DH = КС. Но эти отрезки вместе с НК составляют CD. Это позволяет найти DH и KC:
Зная высоту трапеции и ее основания, легко найдем и ее площадь:
Пифагоровы тройки
Возможно, вы уже заметили, что в большинстве школьных задач на применение теоремы Пифагора используются треуг-ки с одними и теми же сторонами. Это треуг-к, чьи стороны имеют длины
Их использование обусловлено тем, что все их стороны выражаются целыми числами. В задачах же, например, с равнобедренным прямоугольным треуг-ком хотя бы одна из сторон обязательно оказывается иррациональным числом.
Прямоугольные треуг-ки, у которых все стороны являются целыми, называют пифагоровыми треугольниками, а длины их сторон именуются пифагоровыми тройками. Получается, что пифагоровыми называются такие тройки натуральных чисел а, b и с, которые при подстановке в уравнение
обращают его в справедливое равенство.
Для удобства такие тройки иногда записывают в скобках.
Например, тройка чисел (3; 4; 5)– пифагорова, так как
Задание. Определите, какие из следующих троек чисел являются пифагоровыми:
Несложно догадаться, что пифагоровых троек существует бесконечно много. Действительно, возьмем тройку (3; 4; 5). Далее умножим все числа, составляющие ее, на два, и получим новую тройку (6; 8; 10), которая также пифагорова. Умножив исходную тройку на 3, получим тройку (9; 12; 15), и она снова пифагорова. Вообще, умножая числа пифагоровой тройки на любое натуральное число, всегда будем получать новую пифагорову тройку. А так как натуральных чисел бесконечно много, то и троек Пифагора также бесконечное количество.
Отдельно выделяют понятие примитивной пифагоровой тройки. Эта такая тройка, числа которой являются взаимно простыми, то есть не имеют общих делителей. Другими словами, примитивная тройка НЕ может быть получена из другой тройки простым умножением ее чисел на натуральное число. В частности, тройка (3; 4; 5)является примитивной, а «производные» от нее тройки (6; 8; 10) и (9; 12; 15) уже не примитивные.
Интересно, что примитивных троек также бесконечно много. Ещё Евклид предложил алгоритм для их поиска, который, однако, не изучается в рамках школьного курса геометрии.
Задание. Докажите, что у любого прямоугольного треуг-ка с целыми длинами сторон все эти длины не могут быть нечетными числами.
Предположим, что такой треуг-к существует. Пусть его стороны равны a, b и c, и эти числа нечетны. Тогда должно выполняться уравнение:
Заметим, что квадрат нечетного числа также является нечетным числом. Поэтому числа а2, b2 и с2 – нечетные. Однако сумма нечетных чисел является уже четной. Поэтому выражение а2 + b2 четное. Таким образом, получается, что равенство
не может быть верным, ведь его левая часть четна, а правая – нечетна. Поэтому пифагоров треуг-к с тремя нечетными сторонами существовать не может.
Обратная теорема Пифагора
По теореме Пифагора из того факта, что в треуг-ке есть прямой угол, следует следующее соотношение между длинами его сторон:
Оказывается, верно и обратное: если в произвольном треуг-ке одна сторона (очевидно, большая из них) равна сумме квадратов двух других сторон, то из этого следует, что такой треуг-к является прямоугольным.
Это утверждение называют обратной теоремой Пифагора. Докажем её. Пусть есть некоторый ∆АВС, для сторон которого выполняется равенство
Так как ∆А1В1С1 прямоугольный, то для него справедлива теорема Пифагора. Найдем с ее помощью гипотенузу:
а именно это мы и доказываем.
Уточним разницу между собственно теоремой Пифагора и только что доказанной обратной ей теореме. В каждой теореме есть две ключевые части:
1) некоторое условие, которое описывает какое-то геометрическое построение;
2) вывод (или заключение), который делается для условия.
В самой теореме Пифагора в качестве условия описывается прямоугольный треугольник. Для него делается вывод – катеты, возведенные в квадрат, в сумме дадут квадрат гипотенузы.
В обратной же теореме условие и вывод меняются местами. В роли условия описывается треугольник, у которого большая сторона, возведенная во 2-ую степень, равна сумме двух других сторон, также возведенная в квадрат. Для этого описания делается вывод – такой треугольник обязательно должен быть прямоугольным.
Заметим, что не всякая обратная теорема является справедливой. Например, одна из простейших теорем гласит – если углы вертикальные, то они равны. Сформулируем обратную теорему – если углы равны, то они вертикальные. Понятно, что это неверное утверждение.
Задание. Выясните, является ли треуг-к прямоугольным, если его стороны имеют длины:
Решение. Здесь надо просто проверить, являются ли эти числа пифагоровыми тройками. Если являются, то соответствующий треуг-к окажется прямоугольным.
Задание. В ∆КМР проведена биссектриса МН. Её длина 12. КМ = 13 и КН = 5. Найдите МР.
Решение. Рассмотрим ∆МНК. Его стороны равны 5, 12 и 13. Но это одна из пифагоровых троек:
Отсюда следует, что треуг-к прямоугольный, причем МК – гипотенуза (гипотенуза – это длиннейшая сторона). Тогда ∠Н = 90°. Но это означает, что биссектриса МН ещё и высота. Но если в треугольнике одна линия одновременно и медиана, и высота, то это равнобедренный треуг-к, причем КР – его основание. Тогда
Формула Герона
Невозможно построить два треугольника с тремя одинаковыми сторонами. Это значит, что теоретически знания трех сторон треугольника достаточно, чтобы найти его площадь. Но как это сделать? Здесь может помочь формула Герона, которая выводится с помощью теоремы Пифагора.
Пусть стороны треуг-ка равны а, b и с, причем с не меньше, чем а и b. В любом треуг-ке есть хотя бы два острых угла, а тупой угол, если он есть, лежит против большей стороны. Это значит, что оба прилегающих кс угла – острые. Отсюда следует, что высота, опущенная нас, будет лежать внутри треуг-ка. Обозначим длину этой высоты как h. Пусть она разобьет сторону сна два отрезка длиной х и у:
По рисунку можно записать три уравнения:
Левая часть одинакова в обоих уравнениях, значит, равны и правые:
С учетом этого выразим h2:
Мы уже выразили высоту (точнее, ее квадрат) через длины сторон. Однако обычно в этой формуле производят замену и вводят число р, равное полупериметру треуг-ка, то есть
Площадь треуг-ка вычисляется по формуле:
Запоминать вывод формулы Герона не надо. Саму формулу всегда можно найти в любом справочнике по геометрии или в Интернете. Достаточно запомнить, что площадь любого треуг-ка можно вычислить, если известны все его стороны.
Задание. Стороны треуг-ка имеют длину 9, 7 и 8 см. Какова его площадь?
Решение. Пусть а = 9; b = 8; с = 7. Для использования формулы Герона сначала вычислим половину периметра треуг-ка:
Итак, сегодня мы узнали о теореме Пифагора. Она представляет собой соотношение, которое связывает катеты и гипотенузу в прямоугольном треуг-ке. Это соотношение помогает в исследованиях других фигур – квадратов, параллелограммов, трапеций. Также с его помощью выведена формула Герона, которая позволяет вычислять площадь треуг-ка, зная только длины его сторон.
Пифагор ((570)–(490) года до н. э.) – древнегреческий математик, мыслитель и философ.
Рис. (1). Пифагор.
Факты биографии Пифагора достоверно не известны. О его жизненном пути можно судить лишь по произведениям других древнегреческих философов. По их мнению, математик Пифагор общался с известнейшими мудрецами, учёными того времени.
Известно, что долгое время Пифагор пробыл в Египте, изучая местные таинства.
Философия Пифагора, его образ жизни привлекли многих последователей, но у философа и учёного было и много противников.
Как математик Пифагор достиг больших успехов. Одна из самых известных геометрических теорем — теорема Пифагора, ему приписывают открытие и доказательство теоремы, создание таблицы Пифагора.
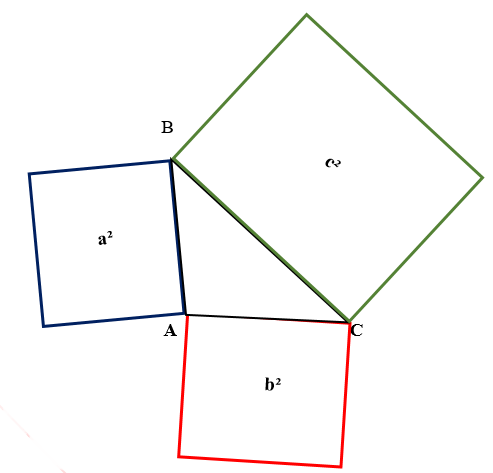
Рис. (2). Теорема Пифагора.
Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
В истории математики находим утверждения, что эту теорему знали за много лет до Пифагора, например, древние египтяне знали о том, что треугольник со сторонами (3), (4) и (5) является прямоугольным.
В наше время теорема звучит так (подразумевая не только площади, но и длины сторон прямоугольного треугольника):
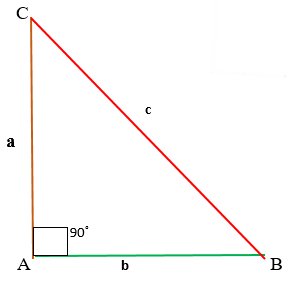
Рис. (3). Прямоугольный треугольник.
В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов
c2=a2+b2
.
Известны очень многие доказательства теоремы разными математическими методами, но одни из самых наглядных связаны с площадями.
1. Построим квадрат, сторона которого равна сумме катетов данного треугольника
a+b
. Площадь квадрата равна
a+b2
:
Рис. (4). Первое доказательство теоремы Пифагора.
2. Если провести гипотенузы (c), очевидно, что они образовали квадрат внутри построенного квадрата.
Стороны четырёхугольника равны (c), а углы — прямые, так как острые углы прямоугольного треугольника в сумме дают
90°
, то угол четырёхугольника также равен
90°
, потому что вместе все три угла дают
180°
.
Следовательно, площадь квадрата состоит из четырёх площадей равных прямоугольных треугольников и площади квадрата, образованного гипотенузами.
Рис. (5). Второе доказательство теоремы Пифагора.
3. На двух сторонах квадрата поменяем местами отрезки (a) и (b), при этом длина стороны квадрата не меняется.
Теперь площадь квадрата можем сложить из двух площадей квадратов, образованных катетами (a) и (b), и двух площадей прямоугольников:
Рис. (6). Третье доказательство теоремы Пифагора.
4. Из этого следуют выводы:
c2+4⋅ab2=(a+b)2;c2+2ab=a2+2ab+b2;
Обрати внимание!
Если находим длину гипотенузы (c), то выполняем сложение квадратов длин катетов (a) и (b) и определяем квадратный корень:
c2=a2+b2;c=a2+b2.
Если находим длину одного катета, то выполняем вычитание длины квадрата другого катета из квадрата длины гипотенузы и определяем квадратный корень:
a2=c2−b2;a=c2−b2.
Обратная теорема используется как признак прямоугольного треугольника.
Если квадрат одной стороны треугольника равен сумме квадратов двух других сторон, то треугольник является прямоугольным.
Пример:
является ли треугольник со сторонами (6) см, (7) см и (9) см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
— значит, этот треугольник не прямоугольный.
Является ли треугольник со сторонами (5) см, (12) см и (13) см прямоугольным?
Выбираем большую сторону и проверяем, выполняется ли теорема Пифагора:
— значит, этот треугольник прямоугольный.
Чтобы не тратить много времени на решение, полезно запомнить наиболее часто используемые числа Пифагора:
катет, катет, гипотенуза
(3), (4), (5);
(6), (8), (10);
(12), (16), (20);
(5), (12), (13).
Посмотри ещё одно своеобразное доказательство теоремы Пифагора:
Рис. (7). Четвёртое доказательство теоремы Пифагора.
Источники:
Рис. 2. Теорема Пифагора. Указание авторства не требуется, 2021-06-05, Наука/Технологии, бесплатно для коммерческого использования, https://clck.ru/VK55r.
Рис. 4, 5, 6. Доказательства теоремы Пифагора, © ЯКласс.
Рис. 7. Четвёртое доказательство теоремы Пифагора, http://linguaggio-macchina.blogspot.com
Теорема Пифагора
О важности теоремы Пифагора высказался Иоганн Кеплер: «Геометрия обладает двумя великими сокровищами: теоремой Пифагора и делением отрезка в крайнем и среднем отношении; первое можно сравнить с мерой золота, второе назвать драгоценным камнем»
Теорема Пифагора актуальна в заданиях как базового, так и профильного ЕГЭ по математике. За верное решение задач базового уровня дается 1 балл, за задания повышенного уровня начисляется 3 балла. В статье мы рассмотрим доказательство теоремы и решим пару задач по теме. Благодаря качественному изучению этого материала экзаменуемый справится с рядом заданий и получит за них наивысший балл.
Что такое теорема Пифагора
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
Важно!
Сторону прямоугольного треугольника, противолежащую прямому углу, называют гипотенузой, а стороны, прилежащие к прямому углу, — катетами. Гипотенуза больше любого из катетов («Геометрия. 8 класс. Учебник», А. Г. Мерзляк).
Формула теоремы Пифагора
c² = a² + b²
Из этой формулы выводятся следующие:
с = √a² + b²
a = √c² — b²
b = √c² — a²
Доказательство теоремы Пифагора

Дано:
△АВС — прямоугольный;
<АСВ = 90⁰.
Доказать:
АВ² = АС² + ВС².
Доказательство:
Проведем высоту СН.
АН, НВ — проекции катетов АС и ВС на гипотенузу. По теореме о метрических соотношениях в прямоугольном треугольнике, квадрат катета равен произведению гипотенузы и проекции этого катета на гипотенузу. Значит,
АС² = АВ × АН; ВС² = АВ × НВ.
Сложим почленно эти равенства:
АС² + ВС² = АВ × АН + АВ × НВ = АВ × (АН + НВ) = АВ ×АВ = АВ².
Что и требовалось доказать.
Задачи на теорему Пифагора
Переходим к решению задач с помощью теоремы Пифагора.
Задача №1
Центр окружности, описанной около треугольника КРH, лежит на стороне КН. Радиус окружности равен 10. Найдите КР, если РН равен 12

Дано:
Описанная окружность с центром в точке О.
О ∈ КН;
R = 10;
РН = 12.
Найти: КР.
Решение:
Так как окружность описанная, то все вершины треугольника лежат на ней. Следовательно, угол <КРН — вписанный.
По условию задачи центр окружности О ∈ КН, значит, хорда КН является диаметром.
КН = 2R = 2 ✕ 10 = 20.
Вписанный угол <КРН, опирающийся на диаметр, — прямой, значит, треугольник КРН — прямоугольный.
По теореме Пифагора:
КР = √КН² — РН²,
КР = √400-144 = √256 = 16
Ответ: КР = 16
Теорема о трех перпендикулярах
Доказательство и формулировка теоремы о трех перпендикулярах
подробнее
Задача №2
Дано:
Пирамида МАВС с высотой МА. Известно, что в основании лежит прямоугольный треугольник с прямым углом С.
Найти:
1) Угол между ребрами МС и ВС. Ответ дайте в градусах.
2) МВ, если МС = 12, ВС = 5.
Решение:
1) Так как по условию задачи МА — высота пирамиды, то МА ⟂ (АВС). АС — проекция наклонной МС на плоскость АВС. Так как АС ⟂ ВС, то, по теореме о трех перпендикулярах, МС ⟂ ВС, следовательно, угол между МС и ВС равен 90° (градусов).
Ответ: 90°.
2) Так как из пункта 1 МС ⟂ ВС ⇒ треугольник МСВ — прямоугольный ⇒ по теореме Пифагора: МВ = √МС² + ВС² ⇒ МВ = √144 + 25 = √169 = 13.
Ответ: МВ = 13.
Популярные вопросы и ответы
Почему теорему Пифагора изучают на геометрии в 8 классе?
Потому что это необходимый теоретический материал для решения задач с помощью данной теоремы: квадратные уравнения, арифметический квадратный корень, подобие треугольников и другие. Эти темы изучаются именно в 8 классе.
Где и когда возникла теорема Пифагора?
Согласно сирийскому историку Ямвлиху, Пифагора познакомили с учителем математики Фалесом Милетским и его учеником Анаксимандром. После известно, что Пифагор отправился в Египет для продолжения своих исследований, был захвачен во время вторжения Камбиса II из Персии в 525 году до н. э. и доставлен в Вавилон. Пифагор вскоре поселился в Кротоне (ныне Кротон, Италия) и основал школу или, говоря современным языком, монастырь, где все члены дали строгий обет хранить тайну, а все новые математические результаты на протяжении нескольких столетий приписывались его имени. Таким образом, до конца неизвестно первое доказательство теоремы, а также есть некоторые сомнения в том, что сам Пифагор действительно ее доказал. Она была одной из первых теорем, пришедших из древних цивилизаций.
Теорема Пифагора — самый известный математический вклад ученого. Согласно одной из легенд, он был так счастлив, когда решил доказательство, что принес в жертву 100 быков.
Также при изучении вавилонских клинописных табличек и древнекитайских рукописей было установлено, что знаменитая теорема была известна задолго до Пифагора, возможно несколько тысячелетий до него. Так, немецкий математик Кантор выяснил, что равенство 32 + 42 = 52 было известно египтянам около 2300 лет до н. э., еще во времена царя Аменехмета (согласно папирусу 6 619 Берлинского музея). Такой треугольник со сторонами 3, 4, 5 получил название «египетский треугольник». Одни предполагают, что Пифагор дал теореме полноценное доказательство, а другие считают по-другому. Например, доказательство в «Началах Евклида» (Предложение 47), по утверждению Прокла, принадлежит самому Евклиду, а не Пифагору.
Где в жизни можно применить теорему Пифагора?
Широкое применение имеет теорема при решении геометрических задач: нахождении длин, расстояний в прямоугольном треугольнике. Большой спектр применения есть у этой великой теоремы в физике, астрономии, строительстве, архитектуре, литературе.
Как звучит обратная теорема Пифагора?
Если квадрат длины одной стороны треугольника равен сумме квадратов длин двух других сторон, то треугольник является прямоугольным.
Изображения на странице: wikipedia.org, Наталия Юмагулова.
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы. Вы узнаете, как доказать теорему, формула Пифагора и как решать задачи.
История теоремы
Однако название получено в честь учёного только по той причине, что он первый и, даже единственный человек, который смог доказать теорему.
Немецкий историк математики Кантор утверждал, что о теореме было известно ещё египтянами приблизительно в 2300 году до н. э. Он считал, раньше строили прямые углы благодаря прямоугольным треугольникам со сторонами 3, 4 и 5.
Известный учёный Кеплер говорил, что у геометрии есть незаменимое сокровище – это теорема Пифагора, благодаря которой можно вывести большинство теорем в геометрии.
Раньше теорему Пифагора называли “теоремой невесты” или “теоремой нимфы”. А всё дело в том, что её чертёж был очень похож на бабочку или нимфу. Арабы же, когда переводили текст теоремы, решили, что нимфа означает невеста. Так и появилось интересное название у теоремы.
Нужна помощь в написании работы?

Мы — биржа профессиональных авторов (преподавателей и доцентов вузов). Наша система гарантирует сдачу работы к сроку без плагиата. Правки вносим бесплатно.
Цена работы
Теорема Пифагора, формула
Теорема Пифагора – в прямоугольном треугольнике сумма квадратов катетов () равна квадрату гипотенузы (
). Это одна из основополагающих теорем эвклидовой геометрии.
Формула:
Как уже говорилось, есть много разнообразных доказательств теоремы с разносторонними математическими подходами. Однако, более часто используют теоремы, связанные с площадями.
Построим на треугольнике квадраты (синий, зеленый, красный)
То есть сумма площадей квадратов, построенных на катетах равняется площади квадрата, построенном на гипотенузе. Соответственно, площади этих квадратов равны – . Это и есть геометрическое объяснение Пифагора.
Доказательство теоремы методом площадей: 1 способ
Докажем, что .
Рассмотрим всё тот же треугольник с катетами a, b и гипотенузой c.
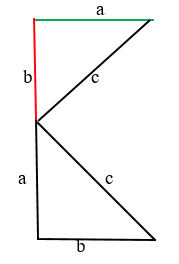
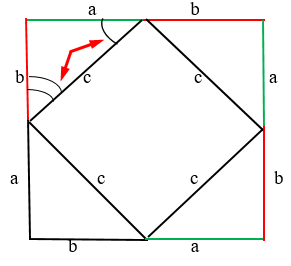
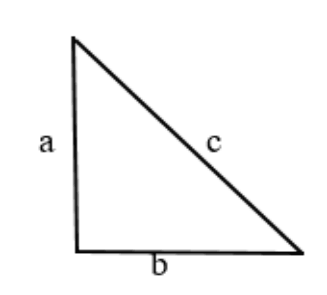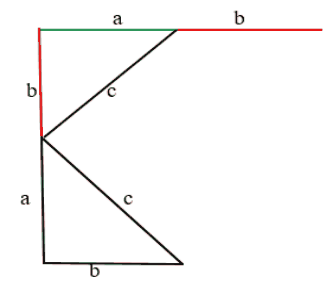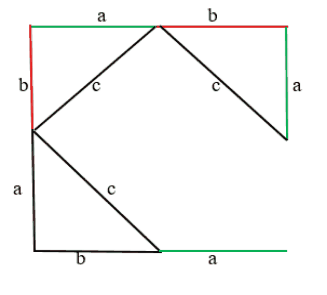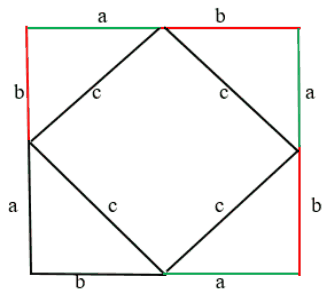
- Достраиваем прямоугольный треугольник до квадрата. От катета “а” продолжаем линию вверх на расстояние катета “b” (красная линия).
- Далее ведём линию нового катета “а” вправо (зелёная линия).
- Два катета соединяем гипотенузой “с”.
Получается такой же треугольник, только перевёрнутый.
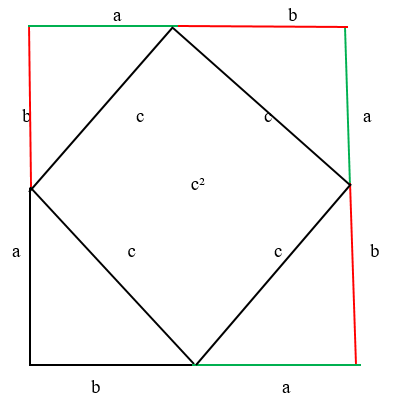
Аналогично строим и с другой стороны: от катета “а” проводим линию катета “b” и вниз “а” и “b” А снизу от катета “b” проводим линию катета “а”. В центре от каждого катета провели гипотенузы “с”. Таким образом гипотенузы образовали квадрат в центре.
Этот квадрат состоит из 4-х одинаковых треугольников. А площадь каждого прямоугольного треугольника = половина произведения его катетов. Соответственно, . А площадь квадрата в центре =
, так как все 4 гипотенузы со стороной
. Стороны четырёхугольника равны, а углы прямые. Как нам доказать, что углы прямые? Очень просто. Возьмём всё тот же квадрат:
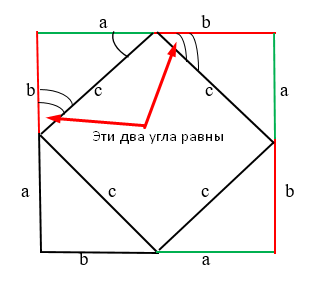
Мы знаем, что эти два угла, показаны на рисунке, являются 90 градусам. Так как треугольники равны, значит следующий угол катета “b” равен предыдущему катету “b”:
Сумма этих двух углов = 90 градусов. Соответственно, предыдущий угол тоже 90 градусов. Конечно же, аналогично и с другой стороны. Соответственно, у нас действительно квадрат с прямыми углами.
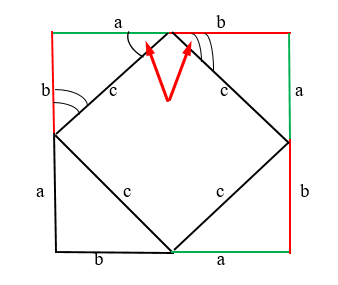
Так как острые углы прямоугольного треугольника в общей сложности равняются 90 градусам, то угол четырёхугольника так же будет равен 90 градусов, ведь 3 угла в сумме = 180 градусов.
Соответственно, площадь квадрата складывается из четырёх площадей одинаковых прямоугольных треугольников и площади квадрата, который образован гипотенузами.
Таким образом, получили квадрат со стороной . Мы знаем, что площадь квадрата со стороной
– это будет квадрат его стороны. То есть
. Этот квадрат состоит из четырёх одинаковых треугольников.
- Запишем:
.
- Далее смотрим, что площадь прямоугольного треугольника – это половина произведения его катетов. Поэтому дальше записываем:т
- Также надо прибавить площадь квадрата, который находится в центре между треугольниками со стороной “с”. И теперь получим:
- Раскрываем скобки и получаем:
- Сокращаем
. Получается:
И это значит, что мы доказали теорему Пифагора.
ВАЖНО!!! Если находим гипотенузу, тогда складываем два катета, а затем ответ выводим из корня. При нахождении одного из катетов: из квадрата длины второго катета вычитаем квадрат длины гипотенузы и находим квадратный корень.
Примеры решения задач
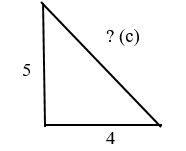
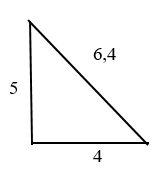
Задача
Дано: прямоугольный треугольник с катетами 4 и 5.
Найдите гипотенузу. Пока её обозначим “с”
Решение
Сумма квадратов катетов равняется квадрату гипотенузы. В нашем случае –
.
Воспользуемся теоремой Пифагора:
Итак, , а
. Катеты в сумме получают 41.
Тогда . То есть квадрат гипотенузы равен 41.
Квадрат числа 41 = 6,4.
Мы нашли гипотенузу.
Ответ
Гипотенуза = 6,4
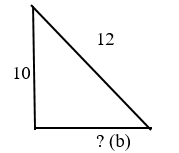
Задача
Дано: прямоугольный треугольник, где гипотенуза = 12, один катет = 10
Найдите второй катет.
Решение
Обозначим неизвестный катет – b.
Воспользуемся теоремой Пифагора:
, а
Запишем:
Находим
Если , тогда просто
Ответ
Второй катет (b) равен 6,6.
Заключение
Итак, мы рассмотрели теорему Пифагора, смогли привести ее доказательство и привели несколько примеров задач и их решений.
Запомните раз и навсегда: квадраты гипотенузы равен суммы квадратов катетов: (это вся теорема Пифагора).