—длина диагонального хода не должна превышать 0,5 максимальной длины хода; относительная погрешность диагонального хода не должна быть больше 1:1000;
—углы в теодолитных ходах измеряют теодолитом не менее 30-секундной точности одним полным приемом с перестановкой лимба между полуприемами примерно на 90о; при измерении углов теодолитами типа Т5 лимб между полуприемами переставляют примерно на 1о – 2о; разница значений углов, полученных в полуприемах не должна превышать 45″;
—центрирование в вершине измеряемого угла выполняется с помощью отвеса или оптического центрира с погрешностью не более 3 мм;
—линии в ходах измеряют стальными лентами или рулетками в прямом и обратном направлениях с установленной относительной погрешностью, либо
впрямом направлении при использовании оптических дальномеров и светодальномеров.
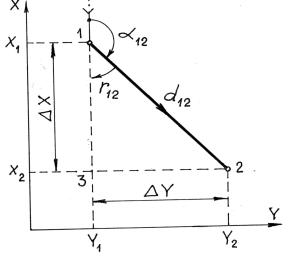
Пусть нам известны координаты точки 1 (Х1, Y1), горизонтальное проложение линии 1-2 d12 и ее дирекционный угол α12 (рис. 7.3). Требуется найти координаты точки 2. Таковы условия прямой геодезической задачи.
|
Прямая геодезическая задача ис- |
||||
|
пользуется для определения коорди- |
||||
|
нат точек местности, в частности, при |
||||
|
определении координат точек теодо- |
||||
|
литных ходов. |
||||
|
Поскольку указанная задача ре- |
||||
|
шается на плоскости (в проекции |
||||
|
Гаусса-Крюгера), то треугольник 123 |
||||
|
является прямоугольным. Линия 1-2 |
||||
|
ориентирована (на рисунке) в круго- |
||||
|
вой (α) и четвертной (r) системах. |
||||
|
Параметры |
Х и |
Y называют |
||
|
Рис. 7.3. Прямая и обратная геодезические |
приращениями координат. |
|||
|
Исходя из геометрии и принятой |
||||
|
задачи на плоскости |
системы координат можно записать, |
|||
|
что |
||||
|
X 2 |
= X1 |
− X |
(7.1) |
|
|
Y2 |
= Y1 + |
Y |
||
Очевидно, что приращения координат должны иметь знак «плюс» или «минус», поскольку координаты точки 2 могут быть больше или меньше координат точки 1. Не обращая внимания на знаки приращений координат, запишем из прямоугольного треугольника
|
X = d12 cos r12 |
(141) |
|
|
Y = d12 sin r12 |
||
|
Принимая во внимание схему рис. 2.19, запишем, что |
168
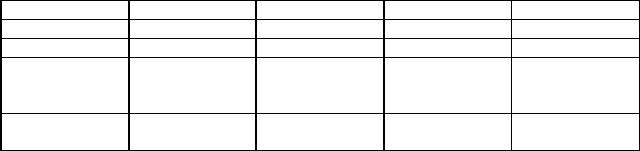
X = d12 cos α Y = d12 sin α
т.е. знаки приращений координат определяются знаками функций sin и cos соответствующих дирекционных углов. Тогда для общего случая формулы (7.1) примут вид
|
X 2 |
= X1 + |
X |
(7.4) |
|
|
Y2 |
= Y1 + |
Y |
||
Пример 7.1. Прямая геодезическая задача.
Исходные данные: Х1 = 4256,324 м; Y1 = 7830,042 м; α12 = 248о39’42»; d12 = 211,656 м. Найти координаты точки 2.
Решение.
|
X 2 |
= |
211,656 ×cos 248 039′42′′ = |
− 77,016 м; |
||
|
Y2 |
= |
211,656 ×sin 248 039′42′′ = |
− 197,147 м; |
||
|
X 2 |
= |
4256 ,324 − 77,016 = |
4179 ,308 м |
||
|
Y2 |
= |
7830 ,042 − 197 ,147 = |
7632 ,895 м. |
Формулировка обратной геодезической задачи: по известным координатам двух точек найти горизонтальное проложение линии, соединяющей эти точки и ее дирекционный угол.
Применительно к рис. 7.3: по известным координатам точек 1 и 2 найти горизонтальное проложение d12 и дирекционный угол α12.
Обратная геодезическая задача используется в большом числе случаев при определении дирекционных углов исходных направлений, а также при решении различных геометрических задач на местности, связанных с построением на местности проектных точек инженерных сооружений (геодезические разбивочные работы).
Установим взаимосвязь между знаками приращений координат и значениями дирекционных углов (табл. 7.2).
|
Таблица 7.2 |
||||
|
Х |
+ |
— |
— |
+ |
|
Y |
+ |
+ |
— |
— |
|
Четверть |
I(СВ) |
II(ЮВ) |
III(ЮЗ) |
IV(СЗ) |
|
Изменения |
||||
|
дирекционного |
0о – 90о |
90о – 180о |
180о – 270о |
270о – 360о(0о) |
|
угла |
α = r |
α = 180o — r |
α = 180o + r |
α = 360o — r |
|
Зависимость |
||||
|
α = f (r ) |
Для решения обратной геодезической задачи вычисляют приращения координат
|
X 2 |
= X 2 − X1 , |
(7.5) |
|
Y2 |
= Y2 − Y1 |
169

если задана задача определения дирекционного угла направления 1-2. Если же необходимо определить дирекционный угол направления 2-1, то приращения координат определяют по формулам
|
X1 |
= X1 − X 2 , |
(7.6) |
|
Y1 |
= Y1 − Y2 |
Далее вычисляют значение румба определяемого направления без учета знаков приращений координат
|
r1− 2(2−1) = arctg |
Y |
(7.7) |
||
|
X |
||||
и по знакам приращений координат, пользуясь таблицей 7.2, выбирают соответствующую формулу для вычисления дирекционного угла.
Дирекционный угол линии можно определить, таким образом, для любого ее направления, а дирекционный угол обратного направления, при необходимости, определяют по формуле обратного ориентирующего угла:
α ОБР = α ПР ± 1800 .
Горизонтальное проложение из прямоугольного треугольника 123 находят по формулам:
|
X 2 |
X1 |
Y2 |
Y1 |
|||||||||||
|
d = |
X |
2 |
+ |
Y |
2 |
= |
= |
= |
= |
|||||
|
. |
(7.8) |
|||||||||||||
|
cosα 12 |
cosα 21 |
sinα 12 |
sinα 21 |
Значения горизонтальных проложений, вычисленных по приведенным формулам, должны практически совпадать в пределах погрешностей округлений.
Пример 7.2. Обратная геодезическая задача.
Исходные данные: Х1 =7273,856 м; Y1 = 5241,656 м; Х2 = 9833,813 м; Y2 = 2165,041 м Найти дирекционный угол направления 1-2 и горизонтальное проложение линии 1-2.
Решение.
Х2 = 9833,813 – 7273,856 = + 2559,957 м. Y2 = 2165,041 – 5241,656 = — 3076,615 м.
(Четвертая четверть – СЗ) – см. табл. 7.2.
|
r1− 2 |
= arctg |
− 3076 |
,615 |
= arctg |
1,201823 = 50 014′14′′ . |
||||||||||||||||||||||
|
+ 2559 |
,957 |
||||||||||||||||||||||||||
|
α 12 |
= |
360 |
0 |
00 |
′ |
00 |
′′ |
0 |
′ |
14 |
′′ |
= |
309 |
0 |
′ |
′′ |
. |
||||||||||
|
− 50 14 |
45 46 |
||||||||||||||||||||||||||
|
= 4002 ,369 м . |
|||||||||||||||||||||||||||
|
d12 |
= |
2559 ,957 2 |
+ 3076 ,615 2 |
||||||||||||||||||||||||
|
d12 |
= |
+ 2559 ,957 |
= |
4002 ,369 м……. d12 |
= |
− 3076 ,615 |
= |
4002 ,365 м . |
|||||||||||||||||||
|
cos 309 0 45′46′′ |
sin 309 0 45′46′′ |
Незначительные расхождения в значениях горизонтального проложения обусловлены погрешностями вычислений при округлении приращений координат и дирекционного угла.
Обратный дирекционный угол α 21 = α 12 ± 1800 = 3090 45′46′′ − 1800 = 1290 45′46′′ .
Этот угол может быть получен и прямым расчетом через соответствующие приращения координат:
Х1= 7273,856– 9833,813 = — 2559,957 м. Y1 = 5241,656–2165,041= + 3076,615 м.
(Вторая четверть – ЮВ) – см. табл. 7.2.
|
r1− 2 |
= arctg |
+ 3076 |
,615 |
= |
arctg |
1,201823 |
= 50 014′14′′ . |
||||||||||||||
|
− 2559 |
,957 |
||||||||||||||||||||
|
α 12 |
= 180 |
0 |
00 |
′ |
00 |
′′ |
0 |
′ |
14 |
′′ |
= 129 |
0 |
′ |
′′ |
. |
||||||
|
− 50 14 |
45 46 |
170
§ 67. Взаимосвязь дирекционных углов с измеренными на местности горизонтальными углами
Для последовательной передачи координат на точки теодолитных ходов необходимо последовательно решать прямые геодезические задачи для каждой из точек, а для этого необходимо знать значения дирекционных углов каждой из линий и их горизонтальные проложения. (Принцип определения горизонтальных проложений изложен в § 71).
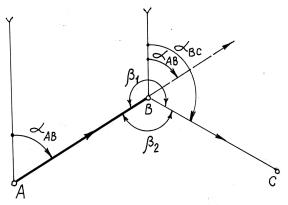
Рассмотрим схему передачи дирекционного угла с линии теодолитного хода на соседнюю с ней линию с использованием измеренного горизонтального угла β в точке поворота (рис. 7.4).
Рис. 7.4. Взаимосвязь дирекционных углов с горизонтальными углами, измеренными на местности
кого построения можно записать, что
Пусть нам известен дирекционный угол линии АВ (αАВ). В точке В поворота измерен горизонтальный угол β1, либо горизонтальный угол β2: (β1 + β2 = 360о). При указанном на схеме направлении хода угол β1 называют левым по ходу углом, а угол β2 –
правым по ходу углом.
Продолжим в точке В линию АВ, достроим в этой точке направление осевого меридиана, параллельного оси Х системы координат, и , в соответствии с определением дирекционного угла, отметим на схеме углы αАВ и αВС. Из полученного геометричес-
|
α ВС |
= α АВ ± 1800 |
+ β 1 |
|
|
α ВС |
= α АВ ± 1800 |
− β 2 . |
(7.9) |
|
Общая формула передачи дирекционного угла с линии на линию имеет |
|||
|
вид: |
= α n ± 1800 |
± β , |
(7.10) |
|
α n+ 1 |
В этой формуле перед значением 180о может оставлять только знак «плюс». Перед значением горизонтального угла β : знак «плюс» — для левых по ходу углов, знак «минус» — для правых по ходу углов.
Ту же задачу удобно решать через дирекционные углы исходящих из точки В линий. Поскольку αАВ ± 180о = αВА, то из (7.9) и (7.10) получим, что
Пример 7.3. Передача дирекционного угла через измеренный горизонтальный угол. 1. Исходные данные: αАВ = 115о36,7′; β (левый по ходу) = 253о14,5′.
Решение 1.
αВС = 115о36,7′ + 180о + 253о14,5′ = 548о51,2′ – 360о = 188о51,2′, поскольку значение дирекционного угла получилось больше 360о.
2. Исходные данные: αАВ = 5о02,7′; β (правый по ходу) = 274о16,8′.
171
Перейти к контенту
Скачать с Depositfiles
2.2 Вычисление горизонтальных проложений (проекций) наклонных длин
Горизонтальное проложение наклонной длины стороны вычисляют по одной из следующих формул:
(3)
или
где L — наклонная длина стороны хода;
— угол наклона стороны;
— поправка за наклон линии;
h — превышение одного конца линии над другим.
Значения длин сторон и углов наклона выбирают из табл. 4 Вычисленные горизонтальных проложений производят в табл. 5
Таблица 5
|
Наименование длин |
Измеренная дайна L,м |
Горизонтал. проложение |
|
Угол наклона |
||
|
В I |
112.97 — 1°58′ |
112.90 |
|
I II |
148.50 — 20131 |
148.39 |
|
II a |
92.03 — 0°35′ |
92.03 |
|
a III |
54.12 + 2°28′ |
54.07 |
|
II III |
— |
145.10 |
2.3. Особенности заполнения ведомости вычисления координат
Вычисления координат вершин теодолитного хода производят г специальной ведомости (табл.6).
Из табл. 4 и 5 в соответствующие графы ведомости выписывает величины измеренных углов и горизонтальные приложения длин сторон полигона.
В графу 4 выписывают среднюю величину дирекционного угла примычной стороны В-1 и координаты точки В (графы 9 и 10).
После занесения в ведомость всех исходных данных приступают к вычислениям. Пример вычислений приведен в табл.6.
Таблица 6 Ведомость вычисления координат точек теодолитного хода (замкнутого)
Р=789,5 +294,97 +246,76
-295,18 -246,72
2.4 Обработка угловых измерений замкнутого теодолитного хода
Обработка угловых намерений заключается в определении величины угловой невязки и в ее распределении в измеренные углы. Вначале определяют фактическую угловую невязку. Дня этого находят сумму измеренных теодолитом углов в замкнутом полигоне, т.е. сумму измеренных углов
.Затем вычисляют теоретическую сумму углов
. Из геометрии известны формулы для подсчета суммы углов многоугольника:
— для внутренних углов;
— для внешних углов.
Фактическая угловая невязка определяется как разность суммы измеренных углов и теоретической суммы углов полигона:
(4)
До распределения угловой невязки следует сначала убедиться, что она не превышает допустимой угловой невязки, которая для полигона с числом вершин nбудет равна:
(5)
Угловая невязка равномерно распределяется во все измеренные углы в виде поправок, сумма которых равна по абсолютной величине фактической невязке, но с противоположным знаком. Следовательно, поправка в один измеренный угол равна
(6)
Поправку вычисляют с точностью до 1 » , поэтому, если фактическая невязка не делится на число углов без остатка, то остаток по одной секунде распределяют на несколько углов. К каждому значению измеренного угла прибавляют (алгебраически) величину поправки и получают значение исправленного угла
Сумма исправленных углов полигона должна быть равна теоретической . Это служит контролем вычислений.
Скачать с Depositfiles
ДЕПАРТАМЕНТ
ОБРАЗОВАНИЯ ЯРОСЛАВСКОЙ ОБЛАСТИ
ГОУ
СПО ЯО РЫБИНСКИЙ ЛЕСХОЗ-ТЕХНИКУМ
Утверждаю
зам.
директора по учебной работе
_________________ Кируца
Е.И.
«____»
_______________ 20 __ г.
МЕТОДИЧЕСКАЯ
РАБОТА
«Решение
задач по геодезии контрольной работы № 1 для студентов заочного отделения»
Тихменево
2020
Кируца
П. Л.,
преподаватель
общепрофессиональных дисциплин, «Решение
задач по геодезии контрольной работы № 1 для студентов заочного отделения», п. Тихменево, 2020 г., 17 стр.
Аннотация
Основной
целью методической разработки является
оказание помощи студентам-заочникам в организации самостоятельной работы по изучению
«Геодезии» в объёме действующей программы. Такая работа требует большого
упорства и умения читать, понимать и применять прочитанное, но в то же время
она способствует дальнейшему развитию умений и навыков самообразования.
Предназначена
преподавателям геодезии.
Методическая
работа рассмотрена на заседании цикловой комиссии общепрофессиональных
дисциплин и рекомендована к использованию в учебном процессе.
Протокол № ____ от ___________
дата
Составитель
работы Кируца Петр Леонидович, преподаватель дисциплины «Геодезия».
Рецензенты:
СОДЕРЖАНИЕ
Введение…………………………………………………………………………………стр.
4
Решение
задач контрольной работы № 1…………………………………………….. стр. 5
Заключение………………………………………………………………………………стр.
16
Список
литературы……………………………………………………………………..стр. 17
ВВЕДЕНИЕ
Геодезия – это наука об измерениях на
земной поверхности, проводимых для определения формы и размеров Земли,
изображения её на планах, картах и профилях, которые используются при решении
инженерных, экономических и других задач.
Эта наука возникла в глубокой древности и развивалась
с ростом потребностей человека в жилье, делении земельных массивов на участки,
строительстве каналов для осушения и орошения, строительстве различных
населенных пунктов, изучении водного режима рек, морей и водных бассейнов,
природных богатств страны, недр Земли и т. д.
Для успешного решения лесохозяйственных задач, кроме
специальных знаний нужны и геодезические знания.
Проведение лесоустройства, восстановление границ землепользований,
отвод площадей под различные виды пользования, строительство лесовозных и
лесохозяйственных дорог, посадка лесных культур и лесных полос требуют от лесовода
знаний и умения пользоваться планами и картами, выполнять геодезические расчёты
и осуществлять перенос в натуру объектов лесохозяйственного пользования.
При изучении данной дисциплины студенты заочного
отделения познакомятся с методами и принципами съемки, съемкой участков
местности и другими видами геодезических работ.
РЕШЕНИЕ
ЗАДАЧ
КОНТРОЛЬНОЙ
РАБОТЫ № 1.
Задача
№ 1. Вычисление расстояний.
Вычислить расстояние, абсолютную и относительную
погрешности его измерения по данным, приведенным в таблице № 1.
Таблица
№ 1
|
№ |
Длина м |
Число |
Число передач |
Число |
Остаток |
|
|
в |
в |
|||||
|
0 |
20 |
6 |
3 |
2 |
3,26 |
2,92 |
|
1 |
24 |
11 |
4 |
3 |
7,43 |
7,66 |
|
2 |
50 |
6 |
3 |
1 |
2,96 |
3,18 |
|
3 |
24 |
11 |
2 |
4 |
4,38 |
4,11 |
|
4 |
20 |
6 |
3 |
3 |
5,26 |
5,54 |
|
5 |
50 |
11 |
4 |
2 |
6,47 |
6,26 |
|
6 |
20 |
6 |
5 |
1 |
8,32 |
8,63 |
|
7 |
24 |
11 |
3 |
5 |
11,02 |
10,81 |
|
8 |
50 |
6 |
2 |
3 |
7,56 |
7,79 |
|
9 |
24 |
11 |
4 |
4 |
3,43 |
3,12 |
Решение:
Расстояние, измеренное мерной лентой, вычисляется по
формуле:
L = ((5)10р
+ n) ℓо+
а, где:
(5)10
– коэффициент, который зависит от числа шпилек в комплекте; если в комплекте 6
шпилек — коэффициент 5, 11 шпилек – коэффициент 10;
р
– число передач шпилек;
n – число
шпилек в руках у заднего мерщика;
ℓо
– длина ленты;
а
– остаток или домер.
Ходовая
линия измерена дважды, в прямом и обратном направлении.
Пример:
Вариант
0.
Lпрямое = (5 · 3 +
2) · 20 + 3,26 = м,
Lобратное.= (5 ∙ 3 +
20) ∙ 20 + 2,92 = м.
Для дальнейшего использования применяется
среднеарифметическая длина ходовой линии
Lср. = = м.
Для определения абсолютной и относительной погрешности
необходимо обращаться к теме «Теория погрешностей».
Абсолютная погрешность указывается в одинаковых
единицах измерения и вычисляется по формуле
∆Lа = Lпрямое – Lобратное = м.
Относительная погрешность указывает на точность
выполнения измерительных работ, записывается в виде дроби
∆Lа =
Пример:
∆Lа = 0,34 м
Lср.А = 424,6
м.
Относительная
ошибка указывает
на то, что на каждые 1248,8 метров, ошибка составляет 1 метр.
Задача № 2.
Вычисление горизонтальных проложений.
По результатам измерения наклонной линии землемерной
лентой и угла наклона эклиметром вычислить горизонтальное проложение этой
линии.
Горизонтальное проложение определяется различными
способами, самый простой по формуле
L’ = L ∙ cos α,
где
L – длина
линии,
α – угол наклона.
Пример:
угол наклона 5,5о равен 5о30’. Для определения значения cos
пользуемся таблицами Брадиса.
Горизонтальные проложения при составлении плана
участка местности необходимо уменьшать в соответствии с масштабом. Численный
масштаб принято изображать в виде дроби с числителем, равным единице, например:
1/1000. Приведённый масштаб означает, что длину линий местности при переносе на
план надо уменьшить в 1000 раз, или по-другому: на план следует откладывать
1/1000 часть измеренной линии местности.
Удобнее пользоваться именованным масштабом. При этом
надо иметь в виду, что в числителе указывают размер на чертеже (плане), а в
знаменателе – соответствующий ему размер в натуре (на местности). Тогда можно
сказать, что 1 см плана соответствует 1000
см = 10 м местности.
Начертим график линейного и поперечного масштабов.
М
1:5000 в 1 см – 50 м 365,33
м : 50 м/см = 7,31 см
При пользовании линейным графиком нередко возникает
необходимость глазомерно определить доли наименьшего деления линейного
масштаба, в результате чего появляются неизбежные погрешности. Чтобы избежать
глазомерного определения десятых долей наименьшего деления масштаба и повысить
точность построений и измерений расстояний на плане чаще применяют поперечный
масштаб.
Для построения поперечного масштаба на горизонтальной
прямой откладывают 5-7 раз основание масштаба, равное 2
см. Из концов отложенных отрезков восстанавливают к прямой перпендикуляры
длиной по 2,5 см. Крайние из них делят на 10 равные частей и соответствующие
точки соединяют прямыми, параллельными нижней линии масштаба. Затем первое
слева основание и противолежащий равный ему отрезок на самой верхней
горизонтальной линии делят также на 10 равных частей и точки этого деления
соединяют наклонными линиями, т.е. трансверсалями.
Чтобы отложить в масштабе 1:5000 длину горизонтального
проложения необходимо:
длину
горизонтального проложения разделить на удвоенное основание масштаба
365,33
м:100 м = 3,653
По графику
откладывают: 3 основания
6 делений влево от
0
5 линий вверх
3 части вверх от 5
линии к шестой на глаз.
Величина масштаба
– расстояние на местности, соответствующее 1
см плана величина М 1:5000 – 50 метров.
Точность масштаба – расстояние на местности,
соответствующее 0,1 мм на плане данного масштаба 1 : 5000 – 0,5 м.
Задача
№ 3. Ориентирование линий.
Зависимость
между азимутом и румбом определяется по следующим формулам:

– 90о, румб в I четверти
называется СВ (северо-восточный)
А
(0о – 90о)
СВ
R = А
СВ R, А = СВ R
Пример:
А = 13о30’
СВ R = А = 13о30’
СВ 60о05’,
А = 60о05’
II четверть А (90о
– 180о), румб во второй четверти называется ЮВ (юго-восточный)
А
(90о – 180о)
ЮВ R = 180о
– А
ЮВ R
А = 180о – ЮВ R
Пример: А = 93о10’
ЮВ
R = 180о
– 93о10’ = 86о50’
ЮВ 24о15’
А
= 180о – ЮВ 24о15’ = 155о45’
III четверть А (180о
– 270о), румб называется ЮЗ (юго-западный)
А (180о – 270о)
ЮЗ R = А – 180о
ЮЗ R
А = 180о + ЮЗ R
Пример: А = 211о25’
ЮЗ
R = 211о25’
– 180о = 31о25’
ЮЗ 25о05’
А
= 180о + ЮЗ 25о05’ = 205о05’
IV четверть А (270о
– 360о), румб называется СЗ (северо-западный)
А (180о – 270о)
СЗ R = 360о
– А
СЗ R
А = 360о – СЗ R
Пример: А = 305о50’
СЗ
R = 360о
– 305о50’ = 54о10’
СЗ 82о20’
А
= 360о – СЗ 82о20’ = 277о40’
Задача № 4.
Составление плана буссольной съёмки по румбам.
Пример.
Результаты измерений во время съёмки заносят в полевой
журнал (таблица № 2) и дублируют их запись для надёжности и наглядности на
схематическом чертеже – абрисе (рис 3), который выполняется в произвольном
масштабе.
Таблица №
2
Журнал
буссольной съёмки
|
№ |
Средний |
Средний |
Длина |
Угол |
Горизонтальное |
|
1-2 |
СВ:13º |
СВ:19º |
57,5 |
7º |
57,1 |
|
2-3 |
СВ:84º |
ЮВ:89º |
57,0 |
0º |
57,0 |
|
3-4 |
ЮВ:19º |
ЮВ:12 |
38,8 |
7º |
38,4 |
|
4-5 |
ЮЗ:46º |
ЮЗ:52º |
50,5 |
0º |
50,5 |
|
5-1 |
СЗ:81º |
СЗ:74º |
51,8 |
0º |
51,8 |
|
пери-метр |
254,8 |
Абрис буссольной съёмки
Измеряют магнитные азимуты (румбы) на местности
приборами, имеющими магнитную стрелку. Она устанавливается в направлении
магнитного меридиана – линии, проходящей через данную точку и магнитные полосы
Земли. Последние не совпадают с географическими. Вследствие этого магнитный и
географический меридианы в общем случае пересекаются между собой, образуя угол d, называемый
магнитным склонением. Оно может быть восточным (положительным) или западным
(отрицательным) в зависимости от направления отклонения магнитного меридиана от
географического.
На лесоустроительных планшетах не показывают магнитных
меридианов, а дают усреднённые сведения о величине магнитного склонения.
Следовательно, измерить по планшету магнитный азимут (румб) нельзя. Как нельзя
нанести на планшет направление по его магнитному азимуту (румбу), измеренному
на местности.
Однако определив на местности магнитный азимут Ам
или румб ( Rм)
заданного направления и учтя магнитное склонение d, легко вычислить
географический (истинный) азимут или румб.
А
= Ам + d
Для определения истинного румба необходимо учитывать
направление и четверть, в которой находится румб.
R = Rм + d (для I и III четверти)
R = Rм — d (для II и IV четверти)
Вычисляем
географические румбы:
R1-2 = СВ :
13º +6º 30´ = СВ : 19º 30´
R2-3 = СВ :
84º +6º 30´ = ЮВ : 89º 30´
R3-4 = ЮВ :
19º — 6º 30´ = ЮВ : 12º 30´
R4-5 = ЮЗ :
46º + 6º 30´ = ЮЗ : 52º 30´
R5-1 = СЗ :
81º — 6º 30´ = СЗ : 74º 30´
Составлять план участка по данным буссольной съёмки,
используя географические румбы, можно в такой последовательности:
- Провести
линию географического меридиана посредине листа бумаги. - Выбрать
с помощью абриса положение первой точки так, чтобы план разместился на
листе бумаги. - Построить
из любой точки меридиана румб первой линии с помощью транспортира. При этом
центр транспортира и отсчёт величины румба должны находиться на меридиане,
а нулевой диаметр транспортира повернут от меридиана по названию румба на
СВ (ЮЗ) или СЗ (ЮВ). - Провести
из первой точки линию, параллельную построенному направлению (рисунок 4),
с помощью треугольника и линейки. - Отложить
на прочерченном направлении размер первой линии по поперечному масштабу,
определив тем самым положение второй точки. - Определить
положение остальных точек последовательно аналогичным построением.
Конец последней линии часто не попадает в первую
точку, т.е. получается линейная невязка, характеризующая качество работы. Для
неё определяют абсолютную (полученную на чертеже) и относительную величину и
сравнивают с допуском. При отводе лесосек допускается погрешность, равная 1/300
части периметра. Для устранения допускаемой невязки надо точку 1´сместить в
точку 1 (рисунок 4), а остальные точки (кроме 1-й) сместить параллельно невязке
и в том же направлении, но на величину, пропорциональную длине от начала хода.
Величину смещения определяют с помощью графика прямой пропорциональной
зависимости. Для этого на прямой линии откладывают в более мелком масштабе
стороны участка. В конце на перпендикуляре откладывают невязку в масштабе плана
и соединяют с первой точкой. Восстанавливают перпендикуляры от остальных точек
до наклонной линии. Полученные отрезки и есть величина смещения для
соответствующих точек.
 |
Примеры построения румбов
|
Для |
Для |
ПЛАН
буссольной
съёмки
масштаб
1:1000
График
распределения линейной невязки
М 1:4000
Пример
расчёта и допустимости линейной невязки.
Абсолютная невязка на чертеже равна 0,8
мм. Согласно масштабу 1:1000 эта же невязка на местности будет равна
1
см
– 10 м 1 мм – 1 м 0,8
мм – 0,8 м
Относительная невязка
|
0,8 |
= |
1 |
< |
1 |
|
254,8 |
318,5 |
300 |
Следовательно, невязка допустима, и её можно устранить
методом параллельных прямых, сопоставив график распределения линейной невязки.
Задача № 5. Определение
площади геометрическим способом.
Для определения площади участка, снятого буссолью и
имеющего неправильную форму, используют известные формулы геометрии для
правильных фигур. С этой целью план разбивают на простейшие фигуры
(треугольники, прямоугольники, трапеции). В расчёте используют готовые размеры
длин сторон, а недостающие измеряют линейкой на плане и по масштабу переводят в
размеры на местности, т.к. нас интересует не площадь плана на бумаге, а площадь
самого участка, изображённого на этом плане. Расчёты для контроля повторяют по
другим элементам фигур или разбивают план по-новому, чтобы не повторить
возможную ошибку.
План
буссольной съемки разбивается на треугольники, близкие к равносторонним. С
помощью масштаба измеряют высоту и основание треугольника и по формуле
S =
вычисляют
площадь фигуры в м2 с переводом в га.
1
способ. Пример.
S1 треугольника = : 10 000 = 0,71 га
S2 треугольника =
S3 треугольника
=
S4 треугольника
=
S5 треугольника
=
2
способ.
Пример.
S1 треугольника = = м2
S2 треугольника =
S3 треугольника
=
S4 треугольника
=
S5 треугольника
=
Sобщ. = S1 +
S2 + S3 + S4 + S5 = 4,61 га.
Пользуясь
двойным определение площадей, вычисляем фактическую невязку.
1.
∆Sa = S1 способ – S2 способ = 4,63 га
– 4,61 га = 0,02 га
2.
Определяем
среднюю арифметическую площадь
Sср.
арифметическая =
3.
Определяем
относительную погрешность
∆Sотносит. =
4.
Допустимая
невязка определения площадей геометрическим способом составляет
∆Sдоп. =
Вывод: Невязка допустима, так как >
.










