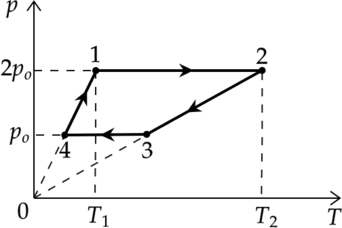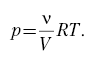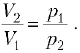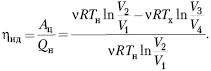135
ЛЕКЦИЯ 12
ПРИМЕНЕНИЕ
ПЕРВОГО НАЧАЛА ТЕРМОДИНАМИКИ
К ИЗОПРОЦЕССАМ
12.1. Изопроцессы.
Работа при изопроцессах
Среди равновесных
процессов, происходящих с термодинамическими
системами, выделяют изопроцессы
– равновесные процессы, в которых один
из основных параметров поддерживается
постоянным.
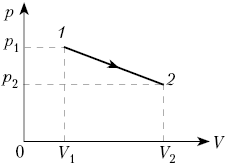
1. Изохорный
процесс ().
1-3 – изохорное
охлаждение; 1-2 – изохорное нагревание.
При
газ не совершает работы:
.
Из первого начала
термодинамики
,
следовательно, первое начало термодинамики
при изохорном процессе:
.
Теплота, сообщенная
газу в изохорном процессе, идет на
изменение (увеличение) внутренней
энергии системы.
2. Изобарный
процесс ().
Из первого начала
термодинамики:
,
следовательно,
первое начало термодинамики при изобарном
процессе:
.
Работа при изобарном
процессе:

Если
К, то для 1 моль газа
,
т.е. R
численно равна работе изобарного
расширения 1 моль идеального газа при
нагревании на 1 К.
3. Изотермический
процесс ().
Первое начало
термодинамики:
.
При
,
,
следовательно,
.
Работа совершается за счет теплоты,
получаемой системой.
Работа изотермического
расширения:
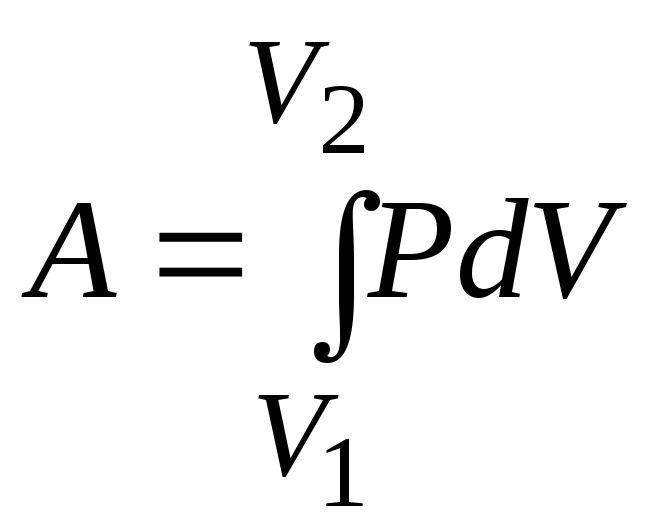
,
следовательно,


следовательно,
работа при изотермическом процессе:
.
Первое начало
термодинамики для изотермического
процесса:
.
Вывод:
все количество теплоты, сообщаемое
газу, расходуется на совершение им
работы против внешних сил.
Чтобы при расширении
газа его температура понижалась, к газу
в ходе изотермического процесса
необходимо подводить количество теплоты,
эквивалентное внешней работе расширения.
12.2. Адиабатный
процесс
К изопроцессам
можно отнести и адиабатный процесс –
процесс, при котором отсутствует
теплообмен с окружающей средой.
Пример:
сжатие и растяжение воздуха в звуковой
волне, работа двигателя внутреннего
сгорания.
полная
теплоизоляция.
Первое начало
термодинамики:
система совершает работу за счет
внутренней энергии системы.
;
(12.1)
Выражение
продифференцируем и получим:
.
(12.2)
Разделим (12.2) на
(12.1):
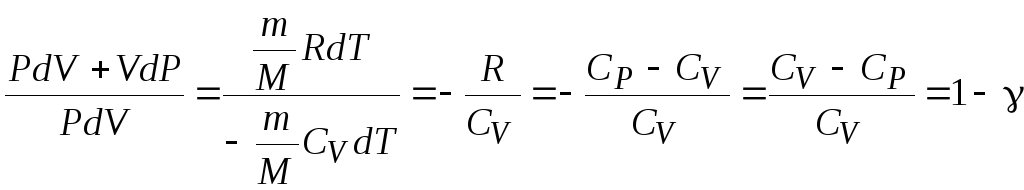
где
.
;
;


Уравнение Пуассона
уравнение
адиабатного процесса в координатах (Р,
V).
Запишем уравнение
Клапейрона-Менделеева и выразим из него
давление P:
,
откуда
‑ уравнение
Пуассона в координатах
(Т,
V).
Выразим из уравнения
Клапейрона-Менделеева объем:
,
откуда
уравнение
Пуассона в координатах
(Т,
Р).
Уравнения адиабатного
процесса:
;
;
,
где
показатель адиабаты.
График адиабаты
– график зависимости между параметрами
состояния идеального газа при
.
Адиабата
более крута, чем изотерма ().
Это объясняется тем, что при адиабатном
сжатии увеличение давления газа
обусловлено не только уменьшением его
объема, как при изотермическом сжатии,
но и повышением температуры, следовательно,
при адиабатном сжатии газ нагревается,
а при адиабатном расширении – охлаждается.
Работа газа в
адиабатном процессе.
.
Работа при адиабатном
процессе:

(12.3)
Вывод:
если газ адиабатически расширяется от
до
,
то его температура уменьшается от
до
.
Учтем:
;
(12.3)
;
(учли, что
)
Учтем:
.


Работа при
адиабатическом процессе расширения
меньше, чем при изотермическом расширении.
Это объясняется тем, что при адиабатном
расширении происходит охлаждение газа,
тогда как при изотермическом расширении
температура поддерживается постоянной
за счет притока извне эквивалентного
количества теплоты.
Вывод: рассматриваемые
изохорный, изобарный, изотермический
и адиабатный процессы имеют общую
особенность – они происходят при
постоянной теплоемкости.
уравнение
изохоры
уравнение
изобары
уравнение
изотермы
уравнение
адиабаты
Процесс, при котором
теплоемкость остается постоянной
называется политропным.
Уравнение политропы:
,
где
показатель политропы;
.
Вывод:
все рассмотренные процессы являются
частными случаями политропного процесса.
В координатах Р, V
политропа – график зависимости между
параметрами состояния при
.
Гипербола ()
занимает промежуточное положение между
изотермой и адиабатой (п
– показатель политропы
).
Контрольные
вопросы
-
Что такое
изопроцессы? Какие изопроцессы Вам
известны? -
Выведите формулы
для подсчета работы при различных
изопроцессах и покажите, как на их
графиках в осях р
,
V
изображается эта работа. -
Нарисуйте (на
плоскости р
,
V
) изотерму и адиабату. Объясните, почему
адиабата с ростом V
спадает круче, чем изотерма? -
Выведите уравнение
Пуассона. Что такое показатель адиабаты? -
За счет чего газ
при адиабатном расширении совершает
работу против внешних сил? Что происходит
с температурой адиабатно расширяющегося
идеального газа? -
Что называется
политропным процессом? -
Теплоемкость при
изотермическом процессе равна
.
Что это означает физически
Задачи
-
Масса 16г кислорода
находится при давлении 300 кПа и температуре
27 оС.
После нагревания при постоянном давлении
газ занял объем 10 литров. Найти количество
теплоты, полученное газом, изменение
внутренней энергии газа и работу,
совершенную газом при расширении.
[6142,5
Дж;
4387,5 Дж;
1755 Дж]. -
Двухатомному газу
сообщено количество теплоты 2,093 кДж.
Газ расширяется изобарически. Найти
работу расширения газа. [598 Дж]. -
Азот массой m=56
г, находящийся при нормальных условиях,
расширяется адиабатно, причем объем
газа увеличивается в два раза. Определите:
1) изменение внутренней энергии ΔU
газа; 2) работу расширения А
газа. [ΔU=—2,75
кДж;
А=2,75
кДж]
Соседние файлы в папке 432_lecfiz
- #
- #
- #
- #
- #
- #
- #
- #
- #
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
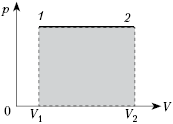
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Первый закон термодинамики» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.
Публикация обновлена:
08.05.2023
1. Изопроцессы и адиабатный процесс
Напомним, что согласно первому закону термодинамики количество теплоты Q, переданное газу, связано с изменением внутренней энергии газа ∆U и работой газа Aг соотношением
Q = ∆U + Aг. (1)
Часто требуется применять первый закон термодинамики к газовым процессам, представляющим собой последовательность изопроцессов (иногда добавляется еще адиабатный процесс).
Рассмотрим, как находить величины, фигурирующие в формуле (1), в этих процессах. Напомним, что каждая из тих величин может быть положительной, отрицательной или равной нулю.
Если график газового процесса задан не в координатах (p, V), то желательно начертить график этого же процесса в координатах (p, V), потому что с помощью этого графика легко найти работу газа. Напомним, что работа газа при расширении численно равна площади под графиком зависимости p(V), при сжатии газа – площади под тем же графиком, но взятой о знаком минус.
В большинстве задач на эту тему рассматривается однотомный идеальный газ. Напомним, что его внутренняя энергия выражается формулой
U = (3/2)νRT, (2)
где ν – количество вещества (число молей), R – универсальная газовая постоянная, T – абсолютная температура.
? 1. Чему равно изменение внутренней энергии газа в изотермическом процессе?
Из формулы (2) и уравнения состояния идеального газа
pV = νRT (3)
следует, что внутреннюю энергию одноатомного идеального газа можно выразить также формулой
U = (3/2)pV. (4)
С помощью этой формулы можно находить изменение внутренней энергии одноатомного идеального газа, если известны начальные и конечные значения давления и объема газа.
Например, если начальные значения давления и объема обозначить p1 и V1, а конечные – p2 и V2, то
∆U = (3/2) (p2V2 – p1V1). (5)
? 2. Чему равно изменение внутренней энергии при изохорном процессе, если объем газа равен V, а давление изменилось от p1 до p2?
? 3. Чему равно изменение внутренней энергии при изобарном процессе, если давление газа равно p, а объем изменился от V1 до V2?
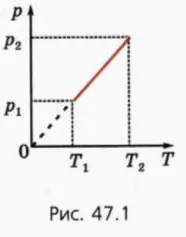
? 4. На рисунке 47.1 изображен график зависимости p(T) для ν молей одноатомного идеального газа при изохорном переходе из состояния 1 в состояние 2. Даны начальные значения давления и температуры газа p1 и T1, конечная температура T2.
а) Чему равно конечное давление газа p2?
б) Чему равен объем газа V?
в) Начертите график этого же процесса в координатах (p, V).
г) Чему равна работа газа Aг?
д) Чему равно изменение внутренней энергии ∆U газа?
е) Чему равно полученное газом количество теплоты Q?
? 5. На рисунке 47.2 изображен график зависимости V(T), для ν молей одноатомного идеального газа при изобарном переходе из состояния 1 в состояние 2. Даны начальные значения объема и температуры газа V1, и T1, конечная температура T2.
47.2
а) Чему равен конечный объем газа V2?
б) Чему равно давление газа p?
в) Начертите график этого же процесса в координатах (p, V).
г) Чему равна работа газа Aг?
д) Чему равно изменение внутренней энергии газа?
е) Чему равно полученное газом количество теплоты Q?
? 6. Используя результаты предыдущих заданий, сравните значения количества теплоты, полученного одним и тем же количеством вещества газа в изохорном и изобарном процессе при нагревании от температуры T1 до температуры T2.
а) В каком случае количество теплоты больше? Во сколько раз больше?
б) Объясните этот результат, используя закон сохранения энергии.
Рассмотрим теперь изотермический и адиабатный процессы.
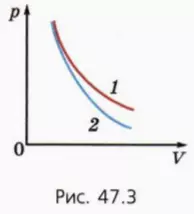
? 7. На рисунке 47.3 приведены графики зависимости p(V) для данной массы газа при изотермическом и адиабатном процессах. Какой график описывает адиабатный процесс? Поясните свой ответ.
? 8. В каком случае совершенная газом работа больше: когда он расширяется изотермически или адиабатно? Начальные объемы газа одинаковы, конечные объемы тоже одинаковы. Поясните свой ответ.
? 9. Как связаны полученное газом количество теплоты Q и работа газа Aг при изотермическом процессе?
Нахождение работы газа при изотермическом расширении выходит за рамки школьного курса физики. Но в задачах часто используется связь между Q и Aг в изотермическом процессе, выведенная вами при выполнении предыдущего задания.
? 10. В вертикальном цилиндре под поршнем массой 1 кг находится идеальный газ. При изотермическом расширении газа поршень поднялся на 5 см. Примите, что трением между поршнем и стенкой цилиндра можно пренебречь.
а) Чему равна работа газа?
б) Чему равно переданное газу количество теплоты?
? 11. Как связаны работа газа Aг и изменение его внутренней энергии ∆U при адиабатном процессе? (Напомним, что при адиабатном процессе отсутствует теплопередача, то есть Q = 0.)
Нахождение работы газа при адиабатном процессе также выходит за рамки школьного курса, но связь между Aг и ∆U в этом процессе широко используется при решении задач.
? 12. При адиабатном расширении 2 молей одноатомного идеального газа газ совершил работу 100 Дж.
а) Как изменилась при этом внутренняя энергия газа?
б) Как изменилась температура газа?
2. Циклические процессы
Циклические газовые процессы состоят из нескольких этапов, причем конечное состояние газа совпадает с начальным. Обычно рассматриваются случаи, когда этапами циклического процесса являются изопроцессы и адиабатный процесс.
Вопросы при этом ставятся, например, такие.
- На каких этапах процесса газ получает тепло, а на каких – отдает?
- Чему равно полученное газом или отданное им количество теплоты?
- Чему равно изменение внутренней энергии газа на различных этапах процесса?
- Чему равна работа газа за один цикл?
- Чему равен КПД цикла?
Для простейшего циклического процесса, состоящего из двух изохор и двух изобар, мы уже нашли ответы на эти вопросы (см. § 43). Рассмотрим теперь более сложный цикл.
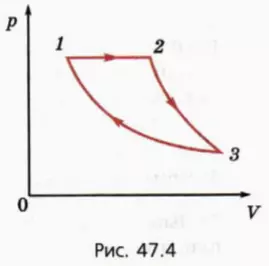
На рисунке 47.4 изображен график циклического процесса, происходящего с некоторой массой одноатомного идеального газа.
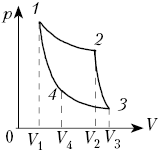
На этапе 2–3 газ адиабатно расширяется, а на этапе 3–1 изотермически сжимается.
Известно, что при изобарном расширении газ совершает работу A, а при изотермическом сжатии отдает холодильнику количество теплоты Qхол. Требуется найти КПД цикла.
Проанализируем сначала этот циклический процесс качественно. По определению КПД цикла равен отношению работы, совершенной газом за один цикл, к количеству теплоты, переданному газу за этот цикл.
Работа, совершенная газом за один цикл, равна разности работы, совершенной газом при его расширении, и работы, совершенной над газом при его сжатии.
? 13. На каких этапах процесса газ совершает работу, а на каких этапах работу совершают над газом?
? 14. На каких этапах процесса газ получает тепло?
Перейдем теперь к количественному описанию. Заметим, то в подобных задачах как работу газа, так и количество теплоты удобно выражать через число молей газа и значения абсолютной температуры газа в различных состояниях газа, даже если эти значения не заданы (в таком случае они сократятся, если найдено правильное решение).
Обозначим T1, T2 и T3 значения абсолютной температуры соответственно в состояниях 1, 2, 3. Поскольку процесс 3–1 изотермический, T1 = T3.
? 15. Рассмотрим сначала изобарный процесс 1–2.
а) Выразите работу газа через давление p в этом процессе и значения объемов газа в состояниях 1 и 2.
б) Выразите эту работу через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
в) Выразите изменение внутренней энергии газа в процессе 1–2 через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
г) Выразите количество теплоты, полученное газом в процессе 1–2, через число молей газа и значения абсолютной температуры в состояниях 1 и 2.
д) Как связано переданное газу количество теплоты с работой, совершенной газом?
? 16. Рассмотрим адиабатный процесс 2–3.
а) Каково соотношение между работой газа в этом процессе и изменением его внутренней энергии?
б) Выразите работу газа в этом процессе через число молей газа и значения абсолютной температуры в состояниях 2 и 3.
в) Найдите соотношение между работой газа в процессе 1–3 и работой газа в процессе 2–3.
? 17. Рассмотрим изотермический процесс 3–1.
а) Найдите соотношение между работой газа в этом процессе и количеством теплоты, полученным газом. Учтите, что в данном случае обе эти величины отрицательны.
б) Выразите работу Aвнеш, совершенную в этом процессе над газом, через количество теплоты Qхол, отданное газом холодильнику.
Используя результаты, полученные при выполнении предыдущих заданий, получаем, что работу Aц, совершенную газом за дин цикл, можно выразить через заданные величины:
3. Расширение газа под поршнем
Трением между поршнем и стенкой сосуда можно пренебречь
Если цилиндрический сосуд с газом расположен вертикально и трением между поршнем и стенками сосуда можно пренебречь, то при медленном нагревании процесс является изобарным. Работа газа
Aг = mgh,
где m – масса поршня, h – расстояние, на которое поднялся поршень. Используя первый закон термодинамики
Q = ∆U + Aг,
можно связать перемещение поршня с переданным газу количеством теплоты Q и изменением его внутренней энергии ∆U. Ее можно выразить через изменение температуры ∆T и число молей газа.
? 18. Одноатомный идеальный газ находится в вертикальном цилиндрическом сосуде под поршнем массой 2 кг. Когда газу передали количество теплоты, равное 10 Дж, поршень поднялся на 5 см, а температура газа увеличилась на 2 К. Трением между поршнем и стенкой сосуда можно пренебречь. Сколько молей газа содержится в сосуде?
Учет трение между поршнем и стенкой сосуда
Типичная ошибка при решении подобных задач состоит в ом, что не учитывают силу трения покоя. Дело в том, что при увеличении давления газа под поршнем он не сдвинется с места до тех пор, пока равнодействующая приложенных к нему сил не превысит максимальную силу трения покоя, которую обычно принимают равной силе трения скольжения. Только поле этого поршень начнет двигаться, и газ начнет расширяться.
Рассмотрим пример. Пусть теперь сосуд расположен горизонтально: в таком случае вес поршня не играет роли.
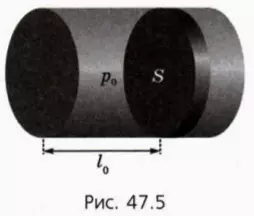
? 19. В горизонтальном цилиндрическом сосуде, закрытом поршнем, находится одноатомный идеальный газ. Начальное давление газа равно p0, начальное расстояние от дна сосуда до поршня равно l0, площадь поршня S (рис. 47.5).
При движении поршня на него со стороны стенки сосуда действует сила трения скольжения Fтр. Будем считать, что сосуд находится в вакууме (то есть на поршень не действует сила атмосферного давления). В начальный момент поршень находится в равновесии. Газу передают некоторое количество теплоты.
а) Какое соотношение между p0, Fтр и S следует из условия, что в начальный момент поршень находится в равновесии?
б) При каком давлении p газа поршень начнет двигаться?
в) Насколько должна увеличиться внутренняя энергия газа, чтобы поршень начал двигаться?
г) Какое количество теплоты Q надо сообщить газу, чтобы поршень начал двигаться?
д) Чему будет равно давление p газа, когда поршень будет двигаться равномерно?
е) Какую работу A совершит газ при равномерном перемещении поршня на расстояние d?
ж) Насколько увеличится при этом внутренняя энергия газа по сравнению с ее начальным значением?
з) Какое количество теплоты Q надо передать газу в начальном состоянии, чтобы поршень сдвинулся на расстояние d?
Дополнительные вопросы и задания
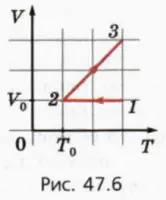
20. На рисунке 47.6 изображен процесс, происходящий с ν молями одноатомного идеального газа.
а) Начертите график этого процесса в координатах (p, V).
б) Чему равны работа газа, изменение его внутренней энергии и переданное ему количество теплоты в процессе 1–2? Учтите, что эти значения могут быть отрицательными.
в) Чему равны работа газа, изменение его внутренней энергии и переданное ему количество теплоты в процессе 2–3?
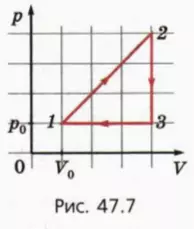
21. На рисунке 47.7 изображен график цикла, происходящего с одноатомным идеальным газом. Найдите КПД цикла.
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Работа идеального газа
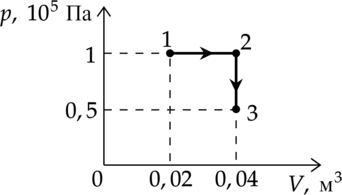
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
Работа газа – площадь под графиком: [A=p_1cdot(V_2-V_1)=10^5text{ Па}cdot(0,04text{ м$^3$}-0,02text{ м$^3$})=2000text{ Дж}=2text{ кДж}]
Ответ: 2
Идеальный газ получил количество теплоты 300 Дж и при этом внутренняя энергия газа увеличилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=300text{ Дж}-100text{ Дж}=200 text{ Дж}]
Ответ: 200
Идеальный газ получил количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=100text{ Дж}-(-100text{ Дж})=200 text{ Дж}]
Ответ: 200
На pV-диаграмме изображены циклические процессы, совершаемые идеальным газом в количестве 1 моль. Определите отношение работы газа в циклическом процессе ВСDВ к работе газа в циклическом процессе АВDFА.
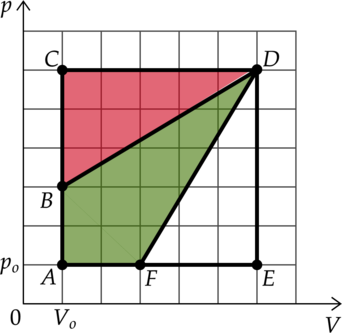
Ответ: 0,75
В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы, сжав газ. Ответ выразите в кДж.
Первое начало термодинамики: [Q=Delta U+A_{text{г}}] [A_{text{г}}=Q-Delta U]
Подставим исходные значения: [A_{text{г}}=Q-Delta U=-10text{ кДж}-30text{ кДж}=-40 text{ кДж}] [A_{text{вн.с.}}=-A_{text{г}}=40 text{ кДж}]
Ответ: 40
В цилиндр с подвижным поршнем накачали (nu = 2) моля идеального одноатомного газа при температуре (t_1 = 50) (^{circ}C). Накачивание вели так, что давление газа было постоянным. Затем накачку прекратили и дали газу в цилиндре расшириться без теплообмена с окружающей средой до давления p = 1 атм. При этом газ остыл до температуры (t_2 = 20) (^{circ}C). Какую суммарную работу совершил газ в этих двух процессах? В исходном состоянии цилиндр был пуст и поршень касался дна. Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ дайте в кДж округлите до целых.
В первом процессе газ расширяется при постоянном давлении. От объема 0 до (V_1) [A_{1-2}=p(V_1-0)=pV_1=nu RT_1]
Без теплообмена с окружающей средой означает, что процесс – адиабатический [Q=Delta U+A_{2-3}=0] [A_{2-3}=-Delta U_{2-3}]
Подставим исходные значения: [A=A_{1-2}+A_{2-3}=nu RT_1+frac{3}{2}nu R(T_1-T_2)=] [=2text{ моль}cdot8,3text{ Дж/моль·К}cdot323text{ K}+frac{3}{2}cdot2text{ моль}cdot8,3text{ Дж/моль·К}cdot30{ K}approx 6000text{ Дж}approx 6 text{ кДж}]
Ответ: 6
С массой (m = 80) г идеального газа, молярная масса которого (M = 28) г/моль, совершается циклический процесс, изображенный на рисунке. Какую работу (A) совершает такой двигатель за один цикл, если (T_1 = 300) К, (T_2 = 1000) К, а при нагревании на участке 4 – 1 давление газа увеличивается в 2 раза? Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ округлите до целых.
1-2 и 3-4 – изобарные процессы
2-3 и 4-1 – изохорные процессы
Перерисуем график в координатах (pV)
Так как 2-3 и 4-1 – изохорные процессы, то (Tsim p). Давление увеличивается в 2 раза, то температура увеличивается в 2 раза. Следовательно: [T_4=frac{T_1}{2}=150 text{ К}] [T_3=frac{T_2}{2}=500 text{ К}]
Работа газа цикл – площадь внутри графика в координатах (pV) [A=(p_1-p_4)cdot(V_2-V_1)=(2p_4-p_4)cdot(V_2-V_1)=p_4cdot(V_2-V_1)=p_4V_2-p_4V_1]
Подставим исходные значения,переведя все единицы в систему СИ: [A=p_4V_2-p_4V_1=nu RT_3-nu RT_4=nu R(T_3-T_4)=frac{m}{M}R(T_3-T_4)=] [=frac{0,08text{ кг}}{0,028text{ кг/моль}}cdot8,31text{ Дж/(моль$cdot$ К)}cdot(500 text{ К} — 150 text{ К})= 8310 text{ Дж}]
Ответ: 8310

УСТАЛ? Просто отдохни
Спецвыпуск
Г. А.
Белуха
Работа газа в термодинамике
··· Орловский выпуск ···
Г.А.БЕЛУХА,
школа № 4, г. Ливны, Орловская обл.
Работа газа в термодинамике
Методические рекомендации по
изучению темы, 10-й класс
При изучении работы газа в
термодинамике учащиеся неизбежно сталкиваются с
трудностями, обусловленными слабыми навыками
вычисления работы переменной силы. Поэтому к
восприятию этой темы необходимо готовиться,
начиная уже с изучения работы в механике и решая
с этой целью задачи на работу переменной силы
путём суммирования элементарных работ на всём
пути с помощью интегрирования.
Например, при вычислениях работы силы
Архимеда, силы упругости, силы всемирного
тяготения и т.п. надо учиться суммировать
элементарные величины с помощью простейших
дифференциальных соотношений типа dA = Fds.
Опыт показывает, что старшеклассники легко
справляются с этой задачей, – дугу траектории, на
которой сила увеличивается или уменьшается,
нужно разбить на такие промежутки ds, на
которых силу F можно считать постоянной
величиной, а затем, зная зависимость F = F(s),
подставить её под знак интеграла. Например,
Работа этих сил вычисляется с помощью
простейшего табличного интеграла
Такая методика облегчает адаптацию
будущих студентов к восприятию курса физики в
вузе и устраняет методические сложности,
связанные с умением находить работу переменной
силы в термодинамике и др.
После того как учащиеся усвоили, что
такое внутренняя энергия и как найти её
изменение, целесообразно дать обобщающую схему:
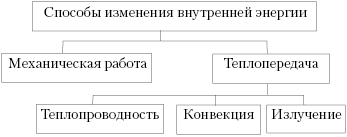
Усвоив, что работа – это один из
способов изменения внутренней энергии,
десятиклассники легко рассчитывают работу газа
в изобарном процессе. На данном этапе необходимо
подчеркнуть, что сила давления газа на всём пути
не меняется, и по третьему закону Ньютона |F2| = |F1|,
знак работы находим из формулы A = Fs cos. Если
= 0°, то A > 0,
если = 180°,
то A < 0. На графике зависимости р(V)
работа численно равна площади под графиком.
Пусть газ расширяется или сжимается
изотермически. Например, газ сжимается под
поршнем, давление изменяется, и в любой момент
времени
При бесконечно малом перемещении
поршня на dl мы получим бесконечно малое
изменение объёма dV, а давление р можно
считать постоянным. По аналогии с нахождением
механической работы переменной силы, составим
простейшее дифференциальное соотношение dA = pdV,
тогда 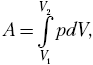
зависимость р (V), запишем 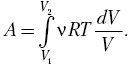
типа 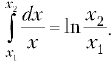
газа в этом случае отрицательна, т.к. = 180°:
т.к. V2 < V1.
Полученную формулу можно переписать,
используя соотношение
Для закрепления решим задачи.
1. Газ переходит из состояния 1
(объём V1, давление р1) в
состояние 2 (объём V2, давление р2)
в процессе, при котором его давление зависит от
объёма линейно. Найдите работу газа.
Решение. Построим примерный
график зависимости p от V. Работа равна
площади под графиком, т.е. площади трапеции:
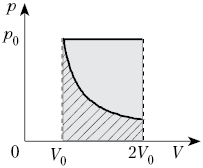
2. Один моль воздуха, находящийся при
нормальных условиях, расширяется от объёма V0
до 2V0 двумя способами – изотермически
и изобарно. Сравните работу, совершённую
воздухом в этих процессах.
Решение
При изобарном процессе Ap = р0V, но р0 =
RT0/V0,
V = V0,
следовательно, Ap = RT0.
При изотермическом процессе:
Сравним:
Изучив первый закон термодинамики и
его применение к изопроцессам и закрепив
решением задач тему о работе в термодинамике,
учащиеся подготовились к восприятию наиболее
сложной части термодинамики «Работа циклов и КПД
тепловых машин». Этот материал я излагаю в
следующей последовательности: работа циклов –
цикл Карно – КПД тепловых машин – круговые
процессы.
процессом (или циклом) называется
термодинамический процесс, в результате
которого тело, пройдя ряд состояний,
возвращается в исходное состояние. Если все
процессы в цикле равновесные, то цикл считается
равновесным. Его можно изобразить графически в
виде замкнутой кривой.
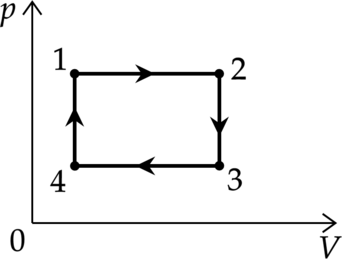
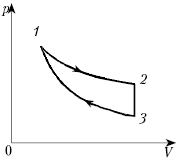
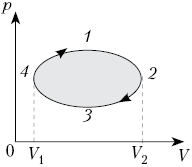
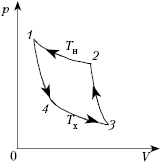
На рисунке показан график зависимости
давления p от объёма V (диаграмма p, V)
для некоторого цикла 1–2–3–4–1. На участках 1–2
и 4–1 газ расширяется и совершает
положительную работу А1, численно
равную площади фигуры V1412V2.
На участке 2–3–4 газ сжимается и совершает
работу А2, модуль которой равен
площади фигуры V2234V1. Полная
работа газ за цикл А = А1 + А2,
т.е. положительна и равна площади фигуры 12341.
Если равновесный цикл изображается
замкнутой кривой на р, V-диаграмме,
которая обходится по часовой стрелке, то работа
тела положительна, а цикл накзывается прямым.
Если замкнутая кривая на р, V-диаграмме
обходится против часовой стрелки, то газ
совершает отрицательную работу за цикл, а цикл
называется обратным. В любом случае модуль
работы газа за цикл равен площади фигуры,
ограниченной графиком цикла на р, V-диаграмме.
В круговом процессе рабочее тело
возвращается в исходное состояние, т.е. в
состояние с первоначальной внутренней энергией.
Это значит, что изменение внутренней энергии за
цикл равно нулю: U = 0.
Так как, по первому закону термодинамики, для
всего цикла Q = U + A, то Q = A.
Итак, алгебраическая сумма всех количеств
теплоты, полученных за цикл, равна работе тела за
цикл: Aц = Qн + Qх = Qн
– |Qх|.
Рассмотрим один из круговых процессов
– цикл Карно. Он состоит из двух изотермических и
двух адиабатических процессов. Пусть рабочим
телом является идеальный газ. Тогда на участке 1–2
изотермического расширения, согласно первому
закону термодинамики, всё получаемое газом тепло
идёт на совершение положительной работы: Q12 = A12.
То есть нет никаких потерь тепла в окружающее
пространство и никакого изменения внутренней
энергии: U = 0,
т.к. T12 = const (потому что газ –
идеальный).
На участке 2–3 адиабатного
расширения газ совершает положительную работу
за счёт изменения внутренней энергии, т.к. Qад = 0
= U23 + Aг23
Aг23 = –
U23.
Здесь также нет потерь тепла, по определению
адиабатного процесса.
На участке 3–4 над газом
совершается положительная работа внешней силой,
но он не нагревается (изотермический процесс).
Благодаря достаточно медленно протекающему
процессу и хорошему контакту с холодильником газ
успевает отдавать получаемую за счёт работы
энергию в виде тепла холодильнику. Сам же газ
совершает при этом отрицательную работу: Q34 = Aг34
< 0.
На участке 4–1 газ адиабатно (без
теплообмена) сжимается до исходного состояния.
При этом он совершает отрицательную работу, а
внешние силы – положительную: 0 = U41 + Aг41
Aг41 = –
U41.
Таким образом, за цикл газ получает
тепло только на участке 1–2, изотермически
расширяясь:
Холодильнику тепло отдаётся только
при изотермическом сжатии газа на участке 3–4:
Согласно первому закону термодинамики
Aц = Qн – |Qx|;
поэтому
КПД машины, работающей по циклу Карно,
найдём по формуле
Согласно закону Бойля–Мариотта для
процессов 1–2 и 3–4, а также уравнению
Пуассона для процессов 2–3 и 4–1, легко
доказать, что
(Хорошо бы увидеть, как автор это
делает: ведь уравнение Пуассона для диабаты
идеального газа надо ещё получить. – Ред.)
После сокращений получим формулу КПД
тепловой машины, работающей по циклу Карно:
обратному циклу, методически правильно, как
показывает опыт, изучать на примере работы
обратного цикла Карно, т.к. он обратим и его можно
провести в обратном направлении: расширять газ
при понижении температуры от Tн до Tx
(процесс 1–4) и при низкой температуре Tx
(процесс 4–3), а затем сжимать (процессы 3–2
и 2–1). Теперь двигатель совершает работу,
чтобы привести в действие холодильную машину.
Рабочее тело отнимает количество теплоты Qx
у продуктов внутри при низкой температуре Tх,
а отдаёт количество теплоты Qн
окружающим телам, за пределами холодильника, при
более высокой температуре Tн. Таким
образом, машина, работающая по обратному циклу
Карно, уже не тепловая, а идеальная холодильная.
Роль нагревателя (отдающего тепло) выполняет
тело с более низкой температурой. Но, сохранив
названия элементов, как в тепловой машине,
работающей по прямому циклу, мы можем
представить блок-схему холодильника в следующем
виде:
Обратим внимание, что тепло от
холодного тела переходит в холодильной машине к
телу с более высокой температурой не
самопроизвольно, а за счёт работы внешней силы.
Важнейшей характеристикой
холодильника является холодильный коэффициент , определяющий
эффективность работы холодильника и равный
отношению количества теплоты, отнятого от
холодильной камеры Qх к затраченной
энергии внешнего источника
За один обратный цикл рабочее тело
получает от холодильника количество теплоты Qх
и отдаёт в окружающее пространство количество
теплоты Qн, что больше Qх на
работу Aдв, совершаемую
электродвигателем над газом за цикл: |Qн| = |Qх| + Адв.
Энергия, затраченная двигателем
(электроэнергия в случае компрессорных
электрических холодильников), идёт на полезную
работу над газом, а также на потери при
нагревании обмоток двигателя электрическим
током QR и на трение в схеме Атр.
Если пренебречь потерями на трение и
джоулево тепло в обмотках двигателя, то
холодильный коэффициент
Учитывая, что в прямом цикле
после несложных преобразований
получим:
Последнее соотношение между
холодильным коэффициентом и КПД тепловой машины,
которая может работать и по обратному циклу,
показывает, что холодильный коэффициент может
быть больше единицы. В этом случае тепла
отнимается от холодильной камеры и возвращается
в комнату больше, чем для этого используется
энергии двигателем.
В случае идеальной тепловой машины,
работающей по обратному циклу Карно (идеального
холодильника), холодильный коэффициент имеет
максимальное значение:
В реальных холодильниках т.к. не вся получаемая
двигателем энергия идёт на работу над рабочим
телом, о чём написано выше.
Решим задачу:
• Оцените стоимость изготовления 1 кг
льда в домашнем холодильнике, если температура
испарения фреона –tх °С,
температура радиатора tн °С.
Стоимость одного киловатт-часа электроэнергии
равна Ц. Температура в комнате t.
Дано:
m, c, t, tн, tх,
, Ц.
____________
Д – ?
Решение
Стоимость Д изготовления льда равна
произведению работы электродвигателя на тариф Ц:
Д = ЦА.
Для превращения воды в лёд с
температурой 0 °С необходимо отвести от неё
количество теплоты Q = m(ct + ). Считаем
приближённо, что над фреоном совершается
обратный цикл Карно с изотермами при
температурах Tн и Tх.
Используем формулы для холодильного
коэффициента: по определению, = Q/A и для
идеального холодильника ид = Tх/(Tн – Tх).
Из условия следует, что
ид.
Решаем совместно три последних
уравнения:
Разбирая с учащимися эту задачу,
необходимо обратить внимание на то, что основная
работа холодильного устройства идёт не на
охлаждение продуктов, а на поддержание
температуры внутри холодильного шкафа путём
периодической откачки тепла, проникающего
сквозь стенки холодильника.
Для закрепления темы можно решить
задачу:
• КПД тепловой машины, работающей по
циклу, состоящему из изотермического процесса 1–2,
изохорического 2–3 и адиабатического 3–1,
равен , а
разность максимальной и минимальной температур
газа в цикле равна T. Найдите работу, совершённую
моль одноатомного
идеального газа в изотермическом процессе.
Решение
При решении задач, в которых
фигурирует КПД цикла, полезно предварительно
проанализировать все участки цикла, используя
первый закон термодинамики, и выявить участки,
где тело получает и отдаёт тепло. Проведём
мысленно ряд изотерм на р, V-диаграмме.
Тогда станет ясно, что максимальная температура
в цикле на изотерме, а минимальная – в т. 3.
Обозначим их через T1 и T3
соответственно.
На участке 1–2 изменение
внутренней энергии идеального газа U2 – U1 = 0.
По первому закону термодинамики, Q12 = (U2 – U1) + А12.
Так как на участке 1–2 газ расширялся, то
работа газа А12 > 0. Значит, и
подведённое к газу количество теплоты на этом
участке Q12 > 0, причём Q12 = А12.
На участке 2–3 работа газа равна
нулю. Поэтому Q23 = U3 – U2.
Воспользовавшись выражениями U2=
cVT1
и тем, что T1 – T3 = T, получим Q23 = –
cV
T < 0.
Это означает, что на участке 2–3 газ получает
отрицательное количество теплоты, т.е. отдаёт
тепло.
На участке 3–1 теплообмена нет,
т.е. Q31 = 0 и, по первому закону
термодинамики, 0 = (U1 – U3) + A31.
Тогда работа газа
A31 = U3 – U1 = cV(T3 –T1) = –
cV
T.
Итак, за цикл газ совершил работу A12 + А31 = А12 – cV
T и получил
тепло только на участке 1–2. КПД цикла
Так как то работа газа на изотерме равна
Геннадий Антонович Белуха –
заслуженный учитель РФ, педагогический стаж 20
лет, ежегодно его ученики занимают призовые
места на различных этапах всероссийской
олимпиады по физике. Хобби – компьютерная
техника.