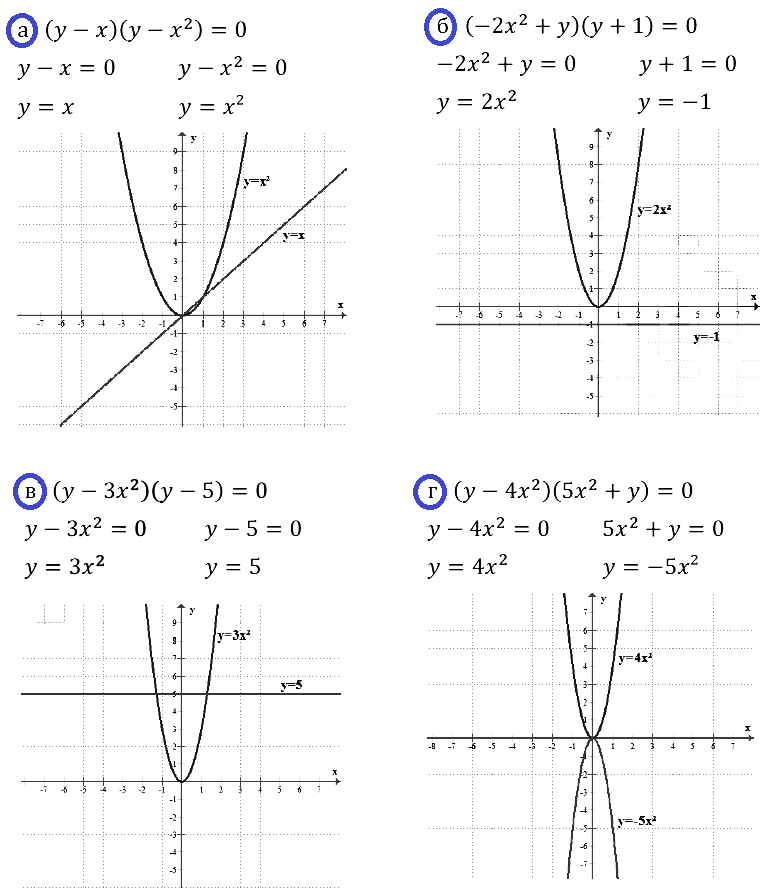
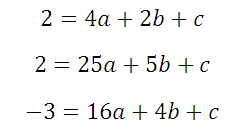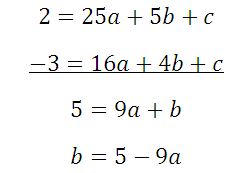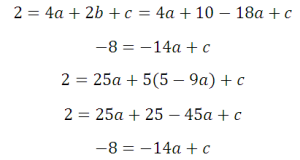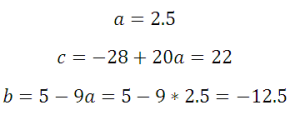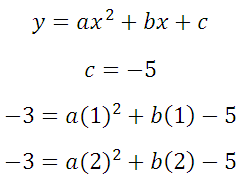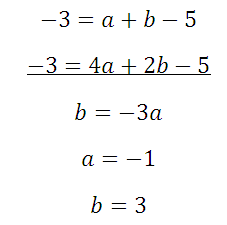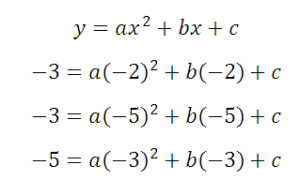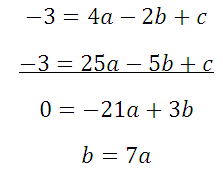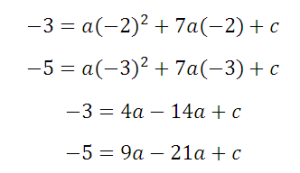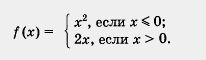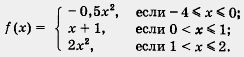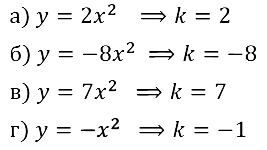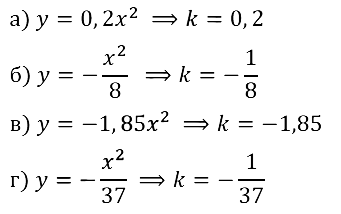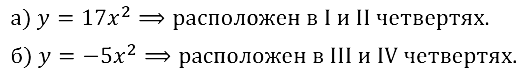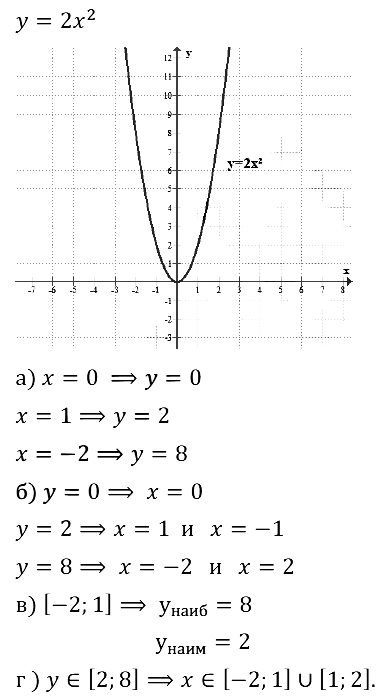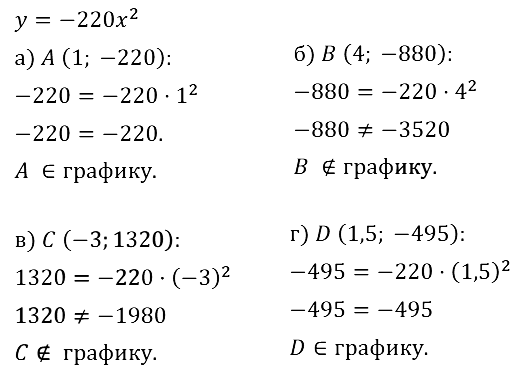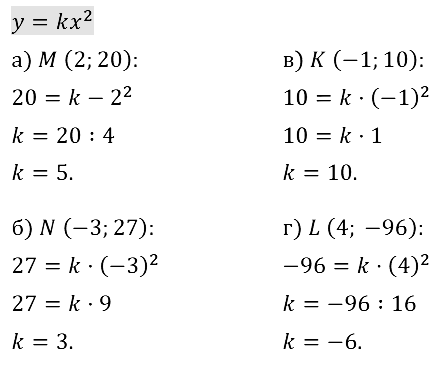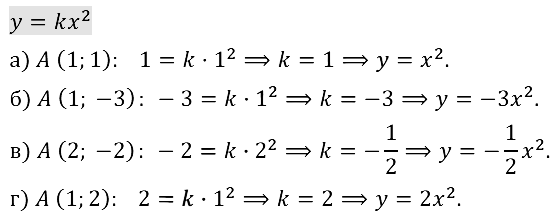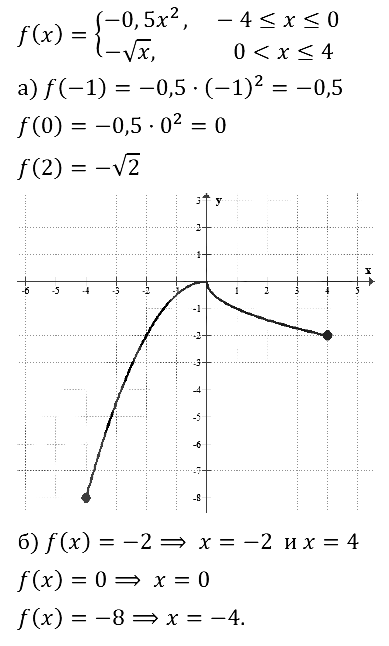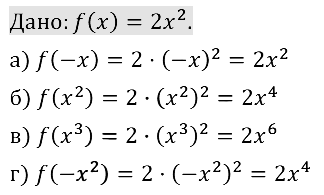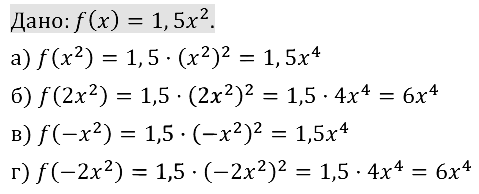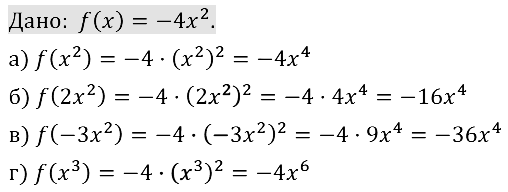Тип урока: урок открытия нового
знания.
Основные цели:
- сформировать представление о функции у = кх2,
ее свойствах и графике; - повторить и закрепить: сведения о функции у =
х2, свойствах функции, известные по курсу
7 класса.
Демонстрационный материал:
1) алгоритм построения графика функции:
1. Заполнить таблицу значений.
2. Построить точки на координатной плоскости.
3. Соединить точки линией.
4. Подписать название функции.
2) Правило определения расположения
графика в зависимости от коэффициента к:
Если к > 0, то парабола расположена в 1
и 2 координатных четвертях или в верхней
полуплоскости;
если к < 0, то парабола расположена в 3 и 4
координатных четвертях или в нижней
полуплоскости.
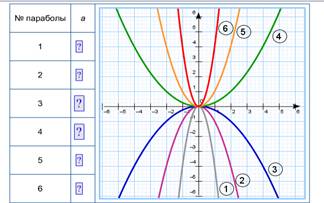
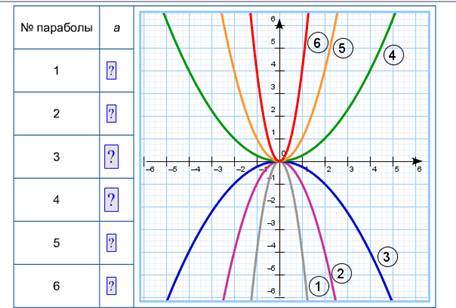
3) самостоятельная работа: На рис.
изображены графики функций у = кх2.
Для каждого графика укажите
соответствующее ему значение коэффициента к.
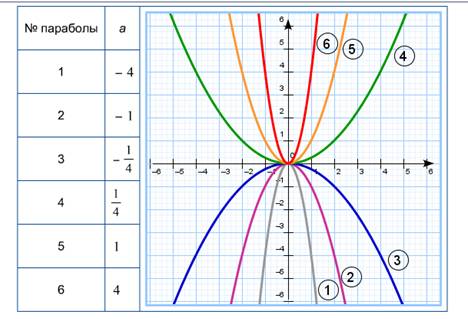
4) образец для самопроверки
самостоятельной работы.
Раздаточный материал:
1) карточка :
1, 2 группа:
Постройте графики функций у = 2х2 ,
у = 4х2 и определите, в каких
координатных четвертях расположены графики
данных функций. Сделайте вывод относительно
коэффициента к.
3, 4 группа:
Постройте графики функций у = –
2х2, у = – 4х2 и
определите, в каких координатных четвертях
расположены графики данных функций. Сделайте
вывод относительно коэффициента к.
2) карточка для рефлексии:
|
Утверждения |
Выполнение |
|
1. Я знаю, что графиком функции у = кх2 |
|
|
2. Я знаю, как определить куда |
|
|
3. Я знаю, как определить область |
|
|
4. Я знаю, как определить промежутки |
|
|
5. Самостоятельную работу я выполнил |
|
|
6. В самостоятельной работе я допустил |
ХОД УРОКА
1. Мотивация к учебной деятельности
Цели:
- организовать актуализацию требований к ученику
со стороны учебной деятельности; - организовать деятельность учащихся по
установке тематических рамок: продолжаем
работать с функциями; - создать условия для возникновения у ученика
внутренней потребности включения в учебную
деятельность.
Организация учебного процесса на
этапе 1:
– Здравствуйте! Что интересного вы
узнали на предыдущих уроках? (Мы изучали
функцию у = | х |, график этой функции и ее
свойства.)
– Сегодня вы продолжите знакомиться с новыми
функциями.
– С каким настроением вы будете работать
сегодня? (С хорошим настроением).
– Успехов Вам!
2. Актуализация знаний и фиксация
затруднения в индивидуальной деятельности
Цели:
- актуализировать учебное содержание,
необходимое и достаточное для восприятия нового
материала. - зафиксировать актуализированные способы
действий в речи и в знаках; - организовать обобщение актуализированных
способов действий; - мотивировать к выполнению индивидуального
задания; - организовать самостоятельное выполнение
индивидуального задания на новое знание; - организовать фиксацию индивидуальных
затруднений в выполнении учащимися
индивидуального задания или в его обосновании.
Организация учебного процесса на
этапе 2:
Проанализируйте несколько слайдов 2-5 и
ответьте на вопрос:
– С каким графиком вы будете работать
сегодня? (С параболой).
– Выберите, графиком какой функции
является парабола у = х + 2, у = 2/х,
у = х2? (у = х2.
Эту функцию мы изучали в 7-м классе).
– Назовите числовой коэффициент
функции у = х2. (Он равен 1)
– В каких координатных четвертях лежит
график функции у = х2 ,какова
область определения и область значений этой
функции, промежутки возрастания и убывания? (График
функции у = х2 лежит в 1 и 2
координатных четвертях или в верхней
полуплоскости, область определения – вся
числовая прямая, область значений – функция
у = х2 принимает
неотрицательные значения; возрастает при х >
0, убывает при х< 0.)
– Обсудим, что происходит при других
значениях коэффициента .
– Сформулируйте тему урока. (Функция
у = кх2, ее свойства и график).
1) На доске приготовлена таблица.
Найдите соответствующие значения функций:
|
х |
– 2 |
– 1 |
0 |
1 |
2 |
|
у = 2х2 |
|||||
|
у =4х2 |
|||||
|
у = – 2х2 |
|||||
|
у = – 4х2 |
– Заполните таблицу. К доске вызываются
последовательно 4 ученика.
2) График функции у = кх2 проходит
через точку А(2;8). Определите значение
коэффициента. Запишите функцию. (к = 2, у = 2х2).
3) По какому плану вы обычно строите
графики функций? Слайд 7.
(Необходимо –
1. Заполнить таблицу значений
2. Построить точки на координатной плоскости
3. Соединить построенные точки плавной линией
4. Подписать название функции.)
– Что вы повторили?
– А теперь, используя всё, что вы только
что повторили и узнали, предлагаю вам выполнить
следующее задание:
Постройте графики функций у = 2х2,
у = – 4х2 и определите, в
каких координатных четвертях расположены
графики данных функций. Сделайте вывод как
расположен график в зависимости от коэффициента
к.
Учащиеся работают на миллиметровой
бумаге.
– У кого нет результата?
– Что вы не смогли сделать? (Я не смог__________________)
– Покажите результаты, кто выполнил построение.
– Как вы можете доказать, что правильно
выполнили задание? (Я должен___________)
– Что вы будете использовать для доказательства?
(____________.)
– Что вы не смогли сделать?
– Каким правилом вы пользовались при построении?
– Что вы не можете сделать?
3. Выявление причин затруднения
Цели:
- организовать соотнесение своих действий с
используемыми эталонами (алгоритмом, понятием и
т.д.); - на этой основе организовать выявление и
фиксацию во внешней речи причины затруднения –
тех конкретных знаний и умений, которых
недостает для решения исходной задачи.
Организация учебного процесса на
этапе 3:
– Какое задание вы должны были
выполнить?
– Что вы использовали при выполнении задания?
– В каком месте возникло затруднение?
– В чём причина затруднения? (У нас нет способа
определения как расположен график функции
у = кх2 в зависимости от коэффициент
к.)
4. Проблемное объяснение нового
знания
Цели:
- организовать постановку цели урока;
- организовать уточнение и согласование темы
урока; - организовать подводящий или побуждающий диалог
по проблемному введению нового знания; - организовать использование предметных
действий с моделями, схемами, свойствами и пр.; - организовать фиксацию нового способа действия
в речи; - организовать фиксацию нового способа действия
в знаках; - соотнесение нового знания с правилом в
учебнике, справочнике, словаре и т.д. - организовать фиксацию преодоления затруднения.
Организация учебного процесса на
этапе 4:
– Сформулируйте цель своей
деятельности. (Найти способ определения как
расположен график функции у = кх2
в зависимости от коэффициента к.)
– Уточните тему урока. (Функция
у = кх2 ,ее свойства и график).
Слайд 6.
– А сейчас вы будете работать в группах:
Слайд 8.
1, 2 группа:
Постройте графики функций у = 2х2,
у = 4х2 и определите, в каких
координатных четвертях расположены графики
данных функций. Сделайте вывод относительно
коэффициента к.
3, 4 группа:
Постройте графики функций у = – 2х2,
у = – 4х2 и определите, в
каких координатных четвертях расположены
графики данных функций. Сделайте вывод
относительно коэффициента к.
Каждой группе даётся карточка. (При
возникновении затруднений учащиеся могут
воспользоваться учебником или справочником.)
– Представьте свой вариант алгоритма.
Каждая из групп представляет свой
вариант, остальные дополняют, уточняют. После
согласования на доску вывешивается правило:
Если к > 0, то парабола расположена в 1
и 2 координатных четвертях или в верхней
полуплоскости (ветви направлены вверх);
если к < 0, то парабола расположена в 3 и 4
координатных четвертях или в нижней
полуплоскости (ветви направлены вниз).
Учитель добавляет:
– Каждую из построенных вами линий
называют параболой. При этом точку (0;0) называют
вершиной параболы, а ось у – осью симметрии
параболы.
От величины коэффициента к зависит «скорость
устремления» ветвей параболы вверх (вниз),
«степень крутизны» параболы.
– Что вы сейчас открыли?
– Что теперь вы должны сделать?
5. Первичное закрепление во внешней
речи
Цель: организовать усвоение
детьми нового способа действий с их
проговариванием во внешней речи.
Организация учебного процесса на
этапе 5:
– В каких координатных четвертях
расположены графики функций у = 1/5х2,
у = х2/2, у = – х2 /2,
у = 3х2?
Задание выполняется в парах, одна пара
работает у доски.
6. Самостоятельная работа с
самопроверкой по образцу
Цели:
- организовать самостоятельное выполнение
учащимися типовых заданий на новый способ
действия; - по результатам выполнения самостоятельной
работы организовать выявление и исправление
допущенных ошибок; - по результатам выполнения самостоятельной
работы создать ситуацию успеха.
Организация учебного процесса на
этапе 6:
Для самостоятельной работы
предлагается задание на карточке. Слайд 9.
На рис. изображены графики функций у
= кх2.
Для каждого графика укажите
соответствующее ему значение коэффициента к.
После выполнения работы учащиеся
проверяют её по образцу: Слайд 10.
– Какие правила вы использовали при
выполнении задания?
– У кого возникло затруднение – как определить
знак коэффициента к?
– У кого возникло затруднение при
определении значения коэффициента к?
– Кто задание выполнил правильно?
7. Включение в систему знаний и
повторение
Цели:
- тренировать навыки использования нового
содержания совместно с ранее изученным
материалом; - повторить учебное содержание, которое
потребуется на следующих уроках:
Организация учебного процесса на
этапе 7:
Задание из ГИА-9 выполняется у доски.
Слайды 11-16.
– Определите термин, который повторялся
много раз сегодня на уроке.(график)
1. Графиком какой из данных функций
является парабола, расположенная в нижней
полуплоскости?
а) у = х2/5
б) у = 5/х2
в) у = 5х
г) у = – 5х2е
в
ш
г
2. Найдите область определения функции
у = –5х2
а) х > 0
б) вся числовая прямая
в) х < 0
г) х < – 5а
р
й
п
3. Найти область значений функции у = – 5х2
а) у < 0
б) у < 0
в) у > 0
г) вся числовая прямаяп
а
ф
ь
4. Ветви какой параболы расположены
дальше от оси ОУ?
а) у = –15х2
б) у = – 9х2
в) у = – х2
г) у = – 5х2ц
э
ф
ж
5. Укажите промежутки возрастания
функции у = – 5х2
а) при х > 0
б) при х < 0
в) при х < 0
г) при х > 0ч
о
и
т
6. Укажите наименьшее значение функции у
= – 5х2
а) 0
б) не существует
в) – 5
г) 5ы
к
д
в.
Задачи по физике: Слайд 17.
Путь, пройденный телом за первые t секунд
свободного падения, вычисляется по формуле: H = gt2/2,
где g = 9,8 м/c2. Найдите по графику
зависимости H от t:
А) расстояние, которое пролетит падающий
камень за первые 6 секунд;
Б) время, за которое камень пролетит первые 250 м?
8. Рефлексия деятельности на уроке
Цели:
- организовать фиксацию нового содержания,
изученного на уроке; - организовать фиксацию степени соответствия
поставленной цели и результатов деятельности; - организовать вербальную фиксацию шагов по
достижению цели; - по результатам анализа работы на уроке
организовать фиксацию направлений будущей
деятельности; - организовать проведение самооценки учениками
работы на уроке; - организовать обсуждение и запись домашнего
задания.
Организация учебного процесса на
этапе 8:
– Чему вы сегодня учились?
– Что нового вы узнали на уроке?
– Какие цели ставили перед собой?
– Вы достигли поставленных целей?
– Что вам помогало справиться с затруднениями?
– Проанализируйте свою работу на уроке.
Учащиеся работают с карточками
рефлексии (Р ).
Домашнее задание: Слайд 18.
- п. П.17 учебника читать
- №17.2,
- №17.3,
- №17.11.
Список литературы:
1. А.Г.Мордкович. Алгебра,8 класс.В
двух частях. Учебник для учащихся
общеобразовательных учреждений. М.:Мнемозина.2011.
2. Интернет-ресурсы.
Как найти k и b по графику линейной функции?
В новой 9 задаче профильного ЕГЭ много заданий на линейные функции. Самое сложное, что нужно сделать, решая эти задачи – определить формулу линейной функции , т.е. найти (k) и (b) по графику. Примеры таких заданий (решения будут внизу статьи):
В статье я расскажу про два простых способа найти (k) и (b), если известен график линейной функции.
Способ 1
Первый способ основывается на трех фактах:
Линейная функция пересекает ось (y) в точке (b).
Примеры:
Но не советую определять так (b), если прямая пересекает ось не в целом значении или если точка пересечения вообще не видна на графике. Для таких случаев пользуйтесь вторым способом.
Если функция возрастает, то знак коэффициента (k) плюс, если убывает – минус, а если постоянна, то (k=0).
Чтоб конкретнее определить (k) надо построить на прямой прямоугольный треугольник так, чтобы гипотенуза лежала на графике функции, а вершины треугольника совпадали с вершинами клеточек. Далее, чтоб определить (k) нужно вертикальную сторону треугольника поделить на горизонтальную и поставить знак согласно возрастанию/убыванию функции.
Давайте пока что не будем искать формулу иррациональной функции, сосредоточимся только на линейной функции.
(b=3) – это сразу видно. Функция идет вниз, значит (k 0). (k=+frac=frac<4><4>=1,b=1). (f(x)=x+1).
Теперь перейдем к функции (g(x)). Найдем координаты точек (D) и (E): (D(-2;4)), (E(-4;1)). Можно составить систему:
Вычтем второе уравнение из первого, чтоб убрать (b):
(g(x)=1,5x+7). Обе функции найдены, теперь можно найти абсциссу (икс) точки пересечения. Приравняем (f(x)) и (g(x)).
Картинку в хорошем качестве, можно скачать нажав на кнопку «скачать статью».
Коэффициенты k и b
Содержание
Положение прямой на графике зависит от величины коэффициентов $k$ и $b$
Коэффициент $k$ называют угловым, так как он показывает угол наклона линейной функции на графике относительно оси $Ox$
При $k > 0$ угол между графиком и осью $Ox$ меньше $90 degree$ (острый)
При $k
Коэффициент b
Коэффициент $b$ называют свободным. На графике он показывает длину отрезка, который отсекает линия функции по оси ординат относительно начала координат.
Другими словами, коэффициент $b$ показывает, насколько график сдвинут вдоль оси $Oy$. Если $b > 0$, то график будет сдвинут вверх, и если $b
Так на нашем графике функции из примера про копилку видно, что прямая пересекает ось $Oy$ выше начала координат на $500$ единиц (этому числу и равен коэффициент $b$).
График функции $y=50x + 500$
Частные случаи. b = 0
В случае, когда коэффициент $b = 0$, а функция прямо пропорциональна, ее график будет проходить через начало координат $O(0;0)$. Ведь при подставлении в формулу $x = 0$ получим и $y = 0$.
Для построения графика такой функции достаточно найти одну точку, вторая – начало координат $О(0;0)$.
Важно: график в виде вертикальной прямой, параллельной оси $Oy$, не является графиком функции. В таком случае одному значению аргумента соответствует множество значений $y$. Это не наш случай, потому что он не соответствует самому определению функции.
При этом прямой, параллельной оси $Ox$, график функции может быть. Это возможно, когда коэффициент $k = 0$. Угол наклона также будет равен $0$. Формула принимает вид $y = b$.
Правила нахождения коэффициентов квадратичной функции

В данной работе рассматриваются правила нахождения коэффициентов (a, b, c) квадратичной функции и их применение на на конкретных примерах.
Просмотр содержимого документа
«Правила нахождения коэффициентов квадратичной функции»
Нахождение коэффициентов квадратичной функции y=ax 2 + bx +c
I Нахождение коэффициента а :
по графику параболы определяем координаты вершины (m,n)
по графику параболы определяем координаты любой точки A (x;y)
подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
решаем полученное уравнение.
II. нахождение коэффициента b: b= — (х1 + х2) это для приведённого уравнения
Сначала находим значение коэффициента a (шаг I, смотри выше)
В формулу для абсциссы параболы m = 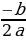
Вычисляем значение коэффициента b.
III. нахождение коэффициента с: с = х1 ∙ х2 это для приведённого уравнения
Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II <находим коэффициенты а,Ь)
Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах 2 +bх+с и находим с.
I Нахождение коэффициента а :
по графику параболы определяем координаты вершины (m,n)
по графику параболы определяем координаты любой точки A (x;y)
подставляем эти значения в формулу квадратичной функции, заданной в другом виде:
решаем полученное уравнение.
II. нахождение коэффициента b:
Сначала находим значение коэффициента a (шаг I, смотри выше)
В формулу для абсциссы параболы m = 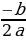
Вычисляем значение коэффициента b.
III. нахождение коэффициента с:
Находим координату у точки пересечения графика параболы с осью Оу, это значение равно коэффициенту с, т.е. точка (0;C)-точка пересечения графика параболы с осью Оу.
Если по графику невозможно найти точку пересечения с осью Оу, то выполняем шаги I, II <находим коэффициенты а,b)
Подставляем найденные значения а, b ,А(х ; у) в уравнение у=ах 2 +bх+с и находим с.
Рассмотрим задачу: где невозможно по графику найти точно m и n необходимо найти все коэффициенты уравнения, задающего график:
Найти все коэффициенты по графику функции
Подставляем в уравнение: 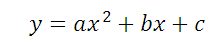
Последние два уравнения вычтем:
Данное выражение подставим в первое и второе уравнения:
Вычтем два получившихся уравнения:
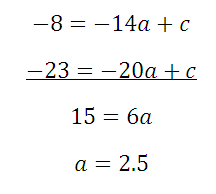
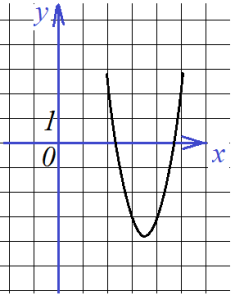
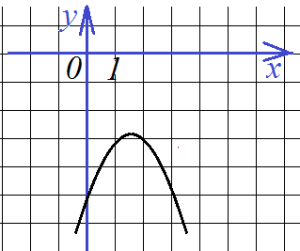
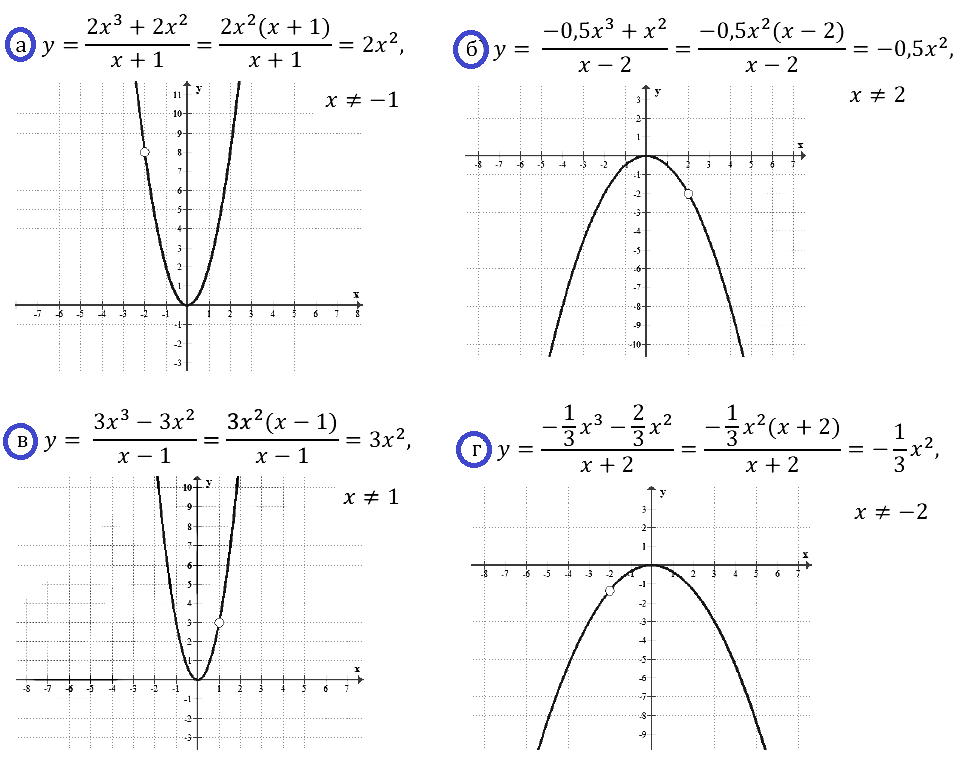
Следующая задача: найти коэффициенты уравнения, задающего график функции, изображенный на рисунке:
Найти все коэффициенты по графику функции
Здесь будет немного попроще, так как определить коэффициент с можно по рисунку: с=-5. Это значит, что потребуется только две точки, и система будет состоять только из двух уравнений. Возьмем для ее составления точки (1;-3) и (2;-3):
Вычтем получившиеся уравнения (второе – из первого) и определим коэффициенты а и b:
Найти все коэффициенты по графику функции
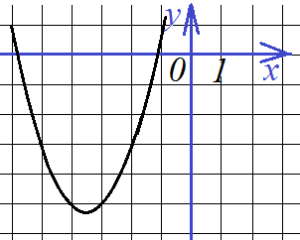
Наконец, еще одно такое же задание. Снова необходимо определить все коэффициенты функции, график которой представлен на рисунке:
Зададимся точками. Их будет три, уравнений тоже три, так как нам необходимо найти три коэффициента – a, b и c.
Точки будут: (-2; -3),(-5; -3) и (-3; -5) . Тогда уравнения:
Из первого уравнения вычитаем второе:
Полученное подставим в первое и третье:
Полученные уравнения вычтем вновь, и найдем искомое:
http://obrazavr.ru/algebra/7-klass-algebra/linejnaya-funktsiya-i-eyo-grafik/linejnaya-funktsiya/koeffitsienty-k-i-b/
http://multiurok.ru/files/pravila-nakhozhdeniia-koeffitsientov-kvadratichnoi.html
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика:Функция у = kx2, ее свойства и график
Функция у = kx2, ее свойства и график
В 7-м классе мы изучали функции у = С, у = kx, у = kx + m, у = х2 и пришли в итоге к выводу о том, что уравнение с двумя переменными вида у = f(x) (функция) есть математическая модель, удобная для того, чтобы, задав конкретное значение независимой переменной х (аргумента), вычислить соответствующее значение зависимой переменной у. Например, если дана функция у = х2, т.е. f(x) = х2, то при х = 1 получаем у = 12 = 1; короче это записывают так: f(1) = 1. При х = 2 получаем f(2)= 22 = 4, т. е. у = 4; при х = — 3 получаем f(- 3) = (- З)2 = 9, т. е. у = 9, и т. д.
Уже в 7-м классе мы с вами начали понимать, что в равенстве у = f(х) правая часть, т.е. выражение f(x), не исчерпывается перечисленными выше четырьмя случаями (С, kx, kx + m, х2).
Так например, нам уже встречались кусочные функции, т. е. функции, заданные разными формулами на разных промежутках. Вот одна из таких функций:у = f(x), где
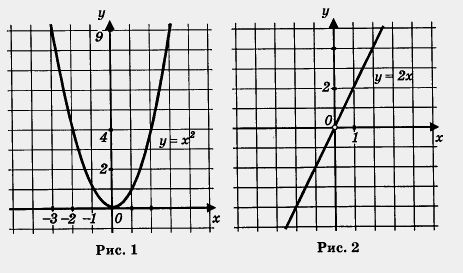
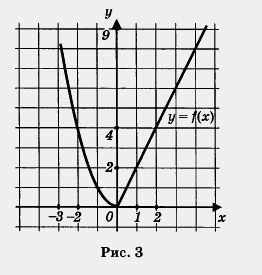
Помните, как строить графики таких функций? Сначала надо построить параболу у = х2 и взять ее часть при х < 0 (левая ветвь параболы, рис. 1), затем надо построить прямую у = 2х и взять ее часть при х > 0 (рис. 2). И, наконец, надо обе выделенные части объединить на одном рисунке, т. е. построить на одной координатной плоскости (см. рис. 3).
Теперь наша задача состоит в следующем: пополнить запас изученных функций. В реальной жизни встречаются процессы, описываемые различными математическими моделями вида у = f(x), не только теми, что мы перечислили выше. В этом параграфе мы рассмотрим функцию у = kx2, где коэффициент k — любое отличное от нуля число.
На самом деле функция у = kx2 в одном случае вам немного знакома. Смотрите: если k = 1, то получаем у = х2; эту функцию вы изучили в 7-м классе и, наверное, помните, что ее графиком является парабола (рис. 1). Обсудим, что происходит при других значениях коэффициента k.
Рассмотрим две функции: у = 2х2 и у = 0,5x2. Составим таблицу значений для первой функции у = 2х2:

Построим точки (0; 0), (1; 2), (-1; 2), (2; 8), (-2; 8), (1,5; 4,5), (-1,5; 4,5) на координатной плоскости (рис. 4); они намечают некоторую линию, проведем ее (рис. 5).
Составим таблицу значений для второй функции у = 0,5x2:
Построим точки (0; 0), (1; 0,5), (-1; 0,5), (2; 2), (-2; 2), C; 4,5), (-3; 4,5) на координатной плоскости (рис. 6); они намечают некоторую линию, проведем ее (рис. 7)
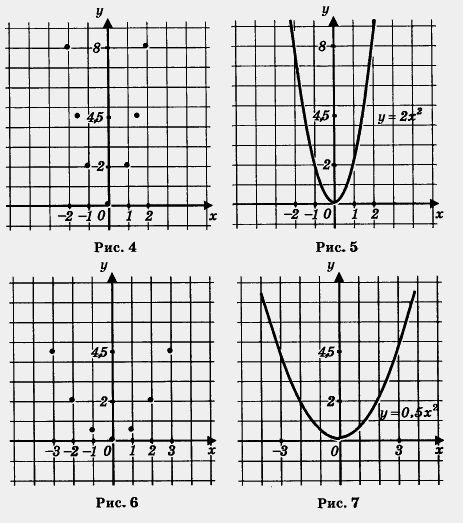
Точки, изображенные на рис. 4 и 6, называют иногда контрольными точками для графика соответствующей функции.
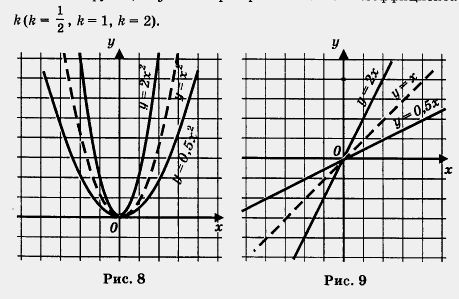
Сравните рисунки 1, 5 и 7. Не правда ли, проведенные линии похожи? Каждую из них называют параболой; при этом точку (0; 0) называют вершиной параболы, а ось у — осью симметрии параболы. От величины коэффициента k зависит «скорость устремления» ветвей параболы вверх или, как еще говорят, «степень крутизны» параболы. Это хорошо видно на рис. 8, где все три построенные выше параболы расположены на одной координатной плоскости.
Точно так же обстоит дело с любой другой функцией вида у = kx2, где k > 0. Графиком ее является парабола с вершиной в начале координат, ветви параболы направлены вверх, причем тем круче, чем больше коэффициент k. Ось у является осью симметрии параболы. Кстати, ради краткости речи математики часто вместо длинной фразы «парабола, служащая графиком функции у = kx2», говорят «парабола у = кх2», а вместо термина «ось симметрии параболы» используют термин «ось параболы».
Вы замечаете, что имеется аналогия с функцией у = kx? Если k > 0, то графиком функции у = kx является прямая, проходящая через начало координат (помните, мы говорили коротко:прямая у = kx), причем и здесь от величины коэффициента k зависит «степень крутизны» прямой. Это хорошо видно на рис. 9, где в одной системе координат изображены графики линейных функций у = kx при трех значениях коэффициента
Вернемся к функции у = kx2. Выясним, как обстоит дело в случае отрицательного коэффициента ft. Построим, например, график функции
у = — х2 (здесь k = — 1). Составим таблицу значении:
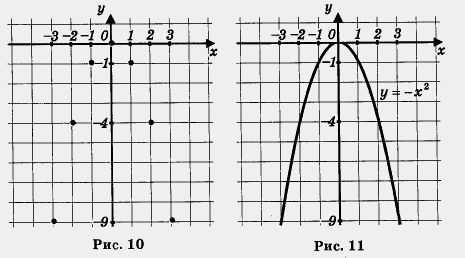
Отметим точки (0; 0), (1; -1), (-1; -1), (2; -4), (-2; -4), (3; -9), (- 3; — 9) на координатной плоскости (рис. 10); они намечают некоторую линию, проведем ее (рис. 11). Это — парабола с вершиной в точке (0; 0), ось у — ось симметрии, но в отличие от случая, когда k > 0, на этот раз ветви параболы направлены вниз. Аналогично обстоит дело и для других отрицательных значений коэффициента k.
Итак, графиком функции является парабола с вершиной в начале координат; ось у является осью параболы; ветви параболы направлены вверх приk>0 u вниз при k<0.
Отметим еще, что парабола у = kx2 касается оси х в точке (0; 0), т. е. одна ветвь параболы плавно переходит в другую, как бы прижимаясь к оси х.
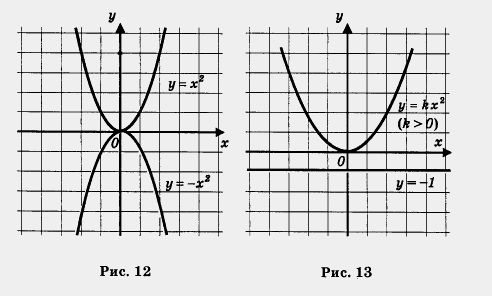
Если построить в одной системе координат графики функций у = х2 и у = — х2, то нетрудно заметить, что эти параболы симметричны друг другу относительно оси х, что хорошо видно на рис. 12. Точно так же симметричны друг другу относительно оси х параболы у = 2х2 и у = — 2х2 (не поленитесь, постройте эти
две параболы в одной системе координат и убедитесь в справедливости сделанного утверждения).
Вообще, график функции у = — f(x) симметричен графику функции у = f(x) относительно оси абсцисс.
Свойства функции у = kx2 при k > 0
Описывая свойства этой функции, мы будем опираться на ее геометрическую модель — параболу (рис. 13).
1. Так как для любого значения х по формуле у = kx2 можно вычислить соответствующее значение у, то функция определена в любой точке х (при любом значении аргумента х). Короче это записывают так: область определения функции есть (-оо, +оо), т. е. вся координатная прямая.
2. у = 0 при х = 0; у > О при . Это видно и по графику функции (он весь расположен выше оси х), но можно обосновать и без помощи графика: если
, то kx2 > О как произведение двух положительных чисел k и х2.
3. у = kx2 — непрерывная функция. Напомним, что этот термин мы рассматриваем пока как синоним предложения «график функции есть сплошная линия, которую можно начертить, не отрывая карандаша от бумаги». В старших классах будет дано более точное математическое истолкование понятия непрерывности функции, не опирающееся на геометрическую иллюстрацию.
4.y/наим = 0 (достигается при х = 0); унаи6 не существует.
Напомним, что {/наим — это наименьшее значение функции, а Унаиб. — наибольшее значение функции на заданном промежутке; если промежуток не указан, то унаим- и унаиб, — соответственно наименьшее и наибольшее значения функции в области определения.
5. Функция у = kx2 возрастает при х > О и убывает при х < 0.
Напомним, что в курсе алгебры 7-го класса мы договорились называть функцию, график которой на рассматриваемом промежутке идет слева направо как бы «в горку», возрастающей, а функцию, график которой на рассматриваемом промежутке идет слева направо как бы «под горку», — убывающей. Более точно можно сказать так: функцию у = f (x) называют возрастающей на промежутке X, если на этом промежутке большему значению аргумента соответствует большее значение функции; функцию у = f (x) называют убывающей на промежутке X, если на этом промежутке большему значению аргумента соответствует меньшее значение функции.
В учебнике «Алгебра—7» процесс перечисления свойств функции мы называли чтением графика. Процесс чтения графика будет у нас постепенно становиться все насыщеннее и интереснее — по мере изучения новых свойств функций. Те пять свойств, которые перечислены выше, мы обсуждали в 7-м классе для изученных там функций. Добавим одно новое свойство.
Функцию у = f(x) называют ограниченной снизу, если все значения функции больше некоторого числа. Геометрически это означает, что график функции расположен выше некоторой прямой, параллельной оси х.
А теперь посмотрите: график функции у = kx2 расположен выше прямой у = — 1 (или у = — 2, это неважно) — она проведена на рис. 13. Значит, у — kx2 (k > 0) — ограниченная снизу функция.
Наряду с функциями, ограниченными снизу, рассматривают и функции, ограниченные сверху. Функцию у — f(x) называют ограниченной сверху, если все значения функции меньше некоторого числа. Геометрически это означает, что график функции расположен ниже некоторой прямой, параллельной оси х.
Имеется ли такая прямая для параболы у = kx2, где k > 0? Нет. Это значит, что функция не является ограниченной сверху.
Итак, мы получили еще одно свойство, добавим его к тем пяти, что указаны выше.
6. Функция у = kx2 (k > 0) ограничена снизу и не ограничена сверху.
Свойства функции у = kx2 при k < 0
При описании свойств этой функции мы опираемся на ее геометрическую модель — параболу (рис. 14).
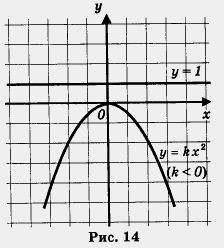
1.Область определения функции — (—оо, +оо).
2. у = 0 при х = 0; у < 0 при .
З.у = kx2 — непрерывная функция.
4. унаи6 = 0 (достигается при х = 0), унаим не существует.
5. Функция возрастает при х < 0, убывает при х > 0.
6.Функция ограничена сверху и не ограничена снизу.
Дадим пояснения последнему свойству: имеется прямая, параллельная оси х (например, у = 1, она проведена на рис. 14), такая, что вся парабола лежит ниже этой прямой; это значит, что функция ограничена сверху. С другой стороны, нельзя провести такую прямую, параллельную оси х, чтобы вся парабола была расположена выше этой прямой; это значит, что функция не ограничена снизу.
Использованный выше порядок ходов при перечислении свойств функции не является законом, пока он сложился хронологически именно таким.
Более-менее определенный порядок ходов мы выработаем постепенно и унифицируем в курсе алгебры 9-го класса.
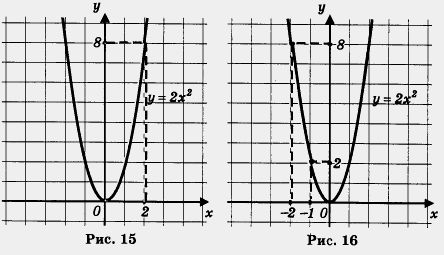
Пример 1. Найти наименьшее и наибольшее значения функции у = 2х2 на отрезке: а) [0, 2]; б) [- 2, — 1]; в) [- 1, 1,5].
Решение.
а) Построим график функции у = 2х2 и выделим его часть на отрезке [0, 2] (рис. 15). Замечаем, что 1/наим. = 0 (достигается при х = 0), а унаиб = 8 (достигается при х = 2).
б) Построим график функции у = 2х2 и выделим его часть на отрезке [- 2, — 1] (рис. 16). Замечаем, что 2/наим = 2 (достигается при х = — 1), а yнаиб = 8 (достигается при х = — 2).
в) Построим график функции у = 2х2 и выделим его часть на отрезке [- 1, 1,5] (рис. 17). Замечаем, что унанм = 0 (достигается при х = 0), а yнаиб достигается в точке х = 1,5; подсчитаем это значение:(1,5) = 2-1,52 = 2- 2,25 = 4,5. Итак, yнаиб =4,5.
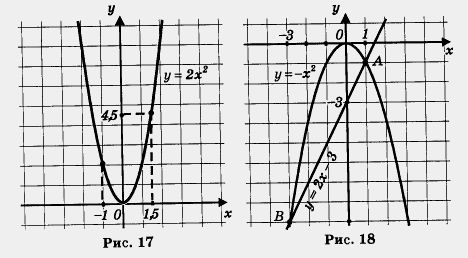
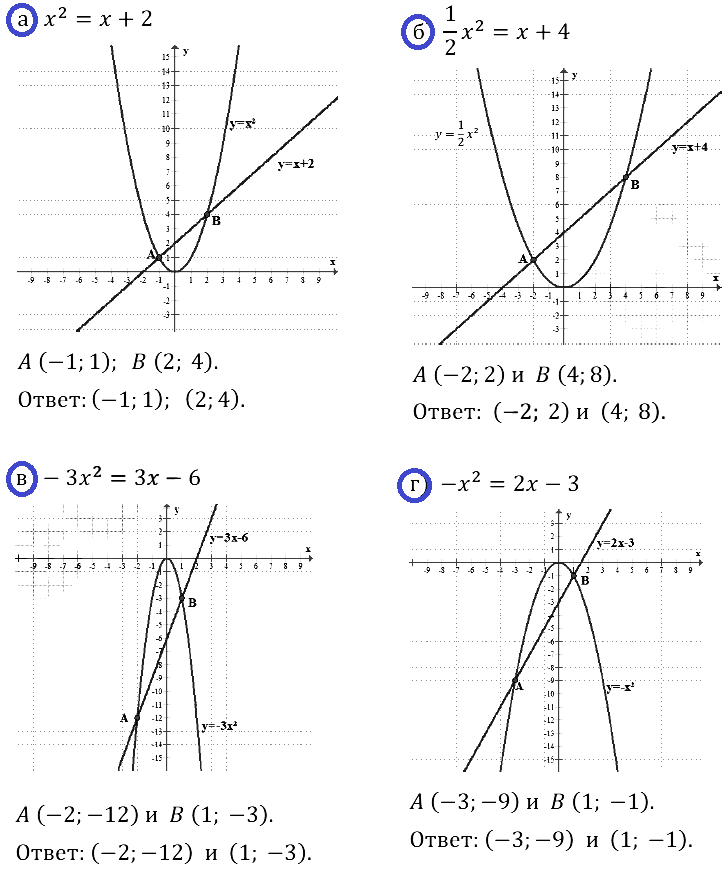
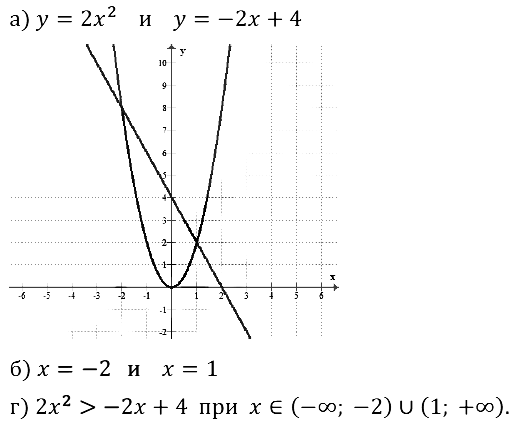
Пример 2. Решить уравнение — х2 = 2х — 3.
Решение. В учебнике «Алгебра—7» мы выработали алгоритм графического решения уравнений, напомним его.
Чтобы графически решить уравнение f(x) = g (x), нужно:
1) рассмотреть две функции у = -x2 и у = 2x -3;
2) построить график функции i/ = / (х) ;
3) построить график функции у = g (x);
4) найти точки пересечения построенных графиков; абсцис-
сы этих точек — корни уравнения f(x) = g (x).
Применим этот алгоритм к заданному уравнению.
1) Рассмотрим две функции: у = — х2 и у = 2х — 3.
2) Построим параболу — график функции у = — х2 (рис. 18).
3) Построим график функции у = 2х — 3. Это — прямая, для ее построения достаточно найти любые две точки графика. Если х = 0, то у = — 3; если х = 1,то у = -1. Итак, нашли две точки (0; -3) и (1; -1). Прямая, проходящая через эти две точки (график функции у = 2х — 3), изображена на том же чертеже (см. рис. 18).
4) По чертежу находим, что прямая и парабола пересекаются в двух точках А(1; -1) и Б(-3; -9). Значит, данное уравнение имеет два корня: 1 и — 3 — это абсциссы точек А и В.
Ответ: 1,-3.
Замечание. Разумеется, нельзя слепо доверять графическим иллюстрациям. Может быть, нам только кажется, что точка А имеет координаты (1; — 1), а на самом деле они другие, например (0,98; — 1,01)?
Поэтому всегда полезно проверить себя. Так, в рассмотренном примере надо убедиться, что точка А(1; —1) принадлежит параболе у = — х2 (это легко — достаточно подставить в формулу у = — х2 координаты точки А; получим — 1 = — 12 — верное числовое равенство) и прямой у = 2х — 3 (и это легко — достаточно подставить в формулу у = 2х — 3 координаты точки А; получим — 1 =2-3 — верное числовое равенство). То же самое надо сделать и для точки 8. Эта проверка показывает, что в рассмотренном уравнении графические наблюдения привели к верному результату.
Пример 3. Решить систему уравнений
Решение. Преобразуем первое уравнение системы к виду у = — х2. Графиком этой функции является парабола, изображенная на рис. 18.
Преобразуем второе уравнение системы к виду у = 2х — 3. Графиком этой функции является прямая, изображенная на рис. 18.
Парабола и прямая пересекаются в точках А(1; -1) и В (- 3; — 9). Координаты этих точек и служат решениями заданной системы уравнений.
Ответ: (1; -1), (-3; -9).
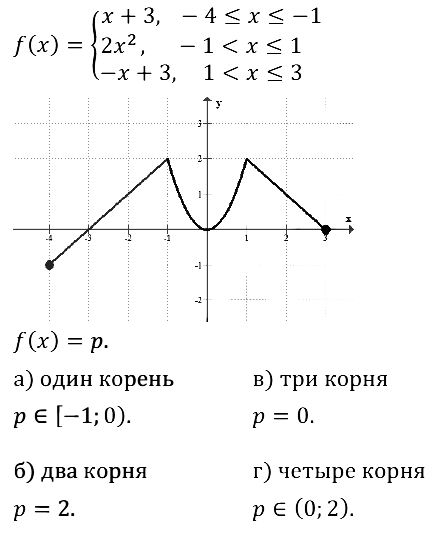
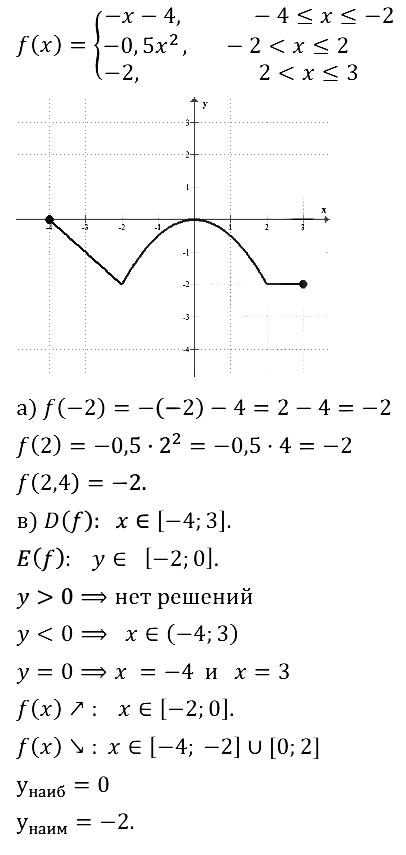
Пример 4. Дана функция у — f (x), где
Требуется:
а) вычислить f(-4), f(-2), f(0), f(1,5), f(2), f(3);
б) построить график функции;
в) с помощью графика перечислить свойства функции.
Решение,
а) Значение х = — 4 удовлетворяет условию —, следовательно, f(-4) надо вычислять по первой строке задания функции.Имеем f(x) = — 0,5×2, значит, f(-4) = -0,5.(-4)2 = -8.
Аналогично находим:
f(-2) = -0,5.(-2)2=-2;
f(0) = -0,5. 02 = 0.
Значение удовлетворяет условию
, поэтому
надо вычислять по второй строке задания функции. Имеем f(х) = х + 1, значит,
Значение х = 1,5 удовлетворяет условию 1 < х < 2, т. е. f(1,5) надо вычислять по третьей строке задания функции. Имеем f (х) = 2х2 , значит, f(1,5) = 2-1,52 = 4,5.
Аналогично получим f(2)= 2.22=8.
Значение х = 3 не удовлетворяет ни одному из трех условий задания функции, а потому f(3) в данном случае вычислить нельзя, точка х = 3 не принадлежит области определения функции. Задание, состоящее в том, чтобы вычислить f(3), — некорректно.
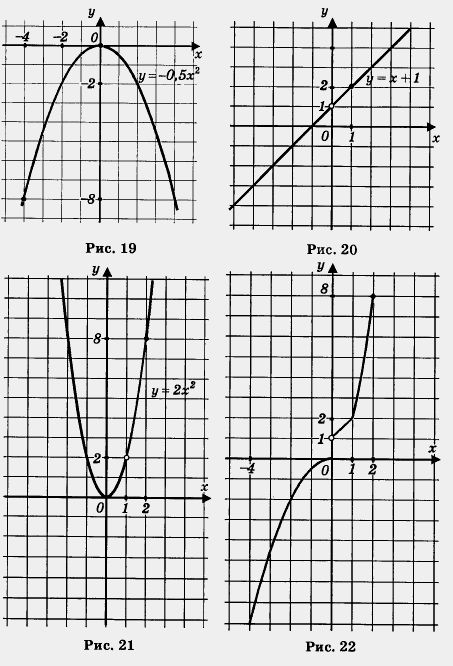
б) Построение графика осуществим «по кусочкам». Сначала построим параболу у = -0,5x2 и выделим ее часть на отрезке [-4, 0] (рис. 19). Затем построим прямую у = х + 1 и. выделим ее часть на полуинтервале (0, 1] (рис. 20). Далее построим параболу у = 2х2 и выделим ее часть на полуинтервале(1, 2] (рис. 21).
Наконец, все три «кусочка» изобразим в одной системе координат; получим график функции у = f(x) (рис. 22).
в) Перечислим свойства функции или, как мы условились говорить, прочитаем график.
1. Область определения функции — отрезок [—4, 2].
2. у = 0 при х = 0; у > 0 при 0<х<2;у<0 при — 4 < х < 0.
3. Функция претерпевает разрыв при х = 0.
4. Функция возрастает на отрезке [-4, 2].
5. Функция ограничена и снизу и сверху.
6. yнаим = -8 (достигается при х = -4); yнаи6. = 8 (достигается при х = 2).
Пример 5. Дана функция у = f(x) , где f(x) = Зх2. Найти:
f(1), f(- 2), f(а), f(2а), f(а + 1), f(-х), f(Зх),f(x — 1),
f(x + а), f(x) + 5, f(х) + b, f(x + а) + b, f(x2), f(2х3).
Решение. Так как f (х) = Зх2, то последовательно получаем:
f(1) =3.12 = 3;
f(a) = За2;
f(а+1) = 3(а + 1)2;
f(3х) = 3.(3х)2 = 27х2;
f(x + а) = 3(х + а)2;
f( x2) +b = 3x2 +b
f(x2) = 3. (x2)2</sup = 3x4
f(- 2) = З.(-2)2 = 12
f( 2a) =З.(2a)2 =12a2
f(x) =З.(-x)2 =3x2
f(-x)+ 5 =3x2 +5
f{x + а) + b = 3 (x + a)2 + b;
f(2x3) = 3. (2x3)2</sup = 12x6
Мордкович А. Г., Алгебра. 8 кл.: Учеб. для общеобразоват. учреждений.— 3-е изд., доработ. — М.: Мнемозина, 2001. — 223 с: ил.
Планирование математике, материалы по математике 8 класса скачать, учебники онлайн
Содержание урокаконспект урока
опорный каркас
презентация урока
акселеративные методы
интерактивные технологии Практика
задачи и упражнения
самопроверка
практикумы, тренинги, кейсы, квесты
домашние задания
дискуссионные вопросы
риторические вопросы от учеников Иллюстрации
аудио-, видеоклипы и мультимедиа
фотографии, картинки
графики, таблицы, схемы
юмор, анекдоты, приколы, комиксы
притчи, поговорки, кроссворды, цитаты Дополнения
рефераты
статьи
фишки для любознательных
шпаргалки
учебники основные и дополнительные
словарь терминов
прочие Совершенствование учебников и уроков
исправление ошибок в учебнике
обновление фрагмента в учебнике
элементы новаторства на уроке
замена устаревших знаний новыми Только для учителей
идеальные уроки
календарный план на год
методические рекомендации
программы
обсуждения Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь — Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний — Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов —
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других «взрослых» тем.
Разработка — Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Описание презентации по отдельным слайдам:
-
1 слайд
«Функция у=кх2 ,ее свойства и график»
Алгебра 8 класс
Учитель математики Шакирова Р.Р. -
2 слайд
Математику уже затем учить надо, что она ум в порядок приводит.
М.В.Ломоносов
-
3 слайд
Девиз урока:
«Дорогу осилит идущий, а математику- мыслящий» -
-
5 слайд
у = kх2 – квадратичная функция, графиком является парабола
(0;0) – вершина параболы
ось у – ось симметрии
k > 0 k < 0
ветви параболы ветви параболы
вверх вниз -
6 слайд
График функции у = -f(x) симметричен графику функции у = f(x) относительно оси абсцисс.
-
7 слайд
Свойства функции у=кх2
при к > 0 -
8 слайд
1.D(f) = (-∞;+∞)
2. у = 0 при х = 0
у > 0 при х є (-∞; 0) U (0;+∞), 3.непрерывна
4.унаим = 0, унаиб = не сущ.
5. убывает при х є (-∞;0],
возрастает при хє [0; +∞)
6.ограничена снизу,
не ограничена сверху
7.Е(f) = [0; +∞)8.выпукла вниз.
-
9 слайд
Свойства функции у = kх2
при k < 0
1. D(f) = (-∞; +∞)
2. у = 0 при х = 0 , У < 0 при х є (-∞; 0) U (0; +∞),
3. Непрерывна
4. Унаим = не сущ., унаиб = 0 (при х=0)
5. возрастает при х є (-∞; 0],
убывает при х є [0; +∞)
6.Ограничена сверху, не ограничена снизу
7. Е(f) = (-∞; 0]
8. выпукла вверх. -
10 слайд
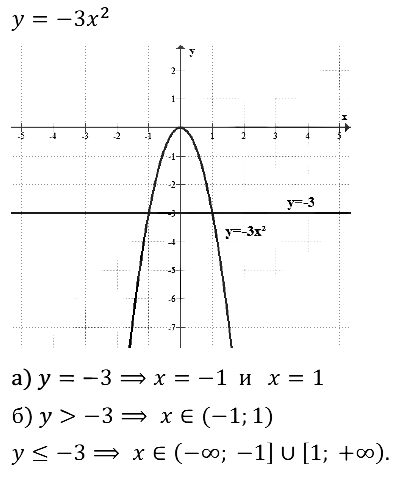
Решите уравнение:
-х2 = 2х — 3
у = -х2 –квадратичная функция, графиком является парабола, ветви которой направлены вниз (k = -1)
у = 2х – 3 – линейная функция, графиком является прямая
Ответ: х = -3; х = 1 -
11 слайд
Вариант 1.
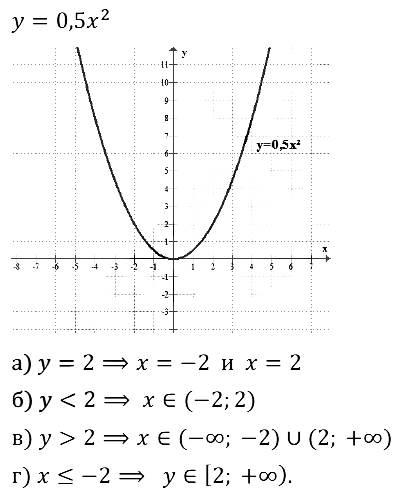
При каком значении аргумента х значение функции у= 0,5х2 равно 2 ?
1)-1 и 1 2) 2 3) -2 и 2
4) -0,5 и 0,5
Графику функции у = -50 х2 принадлежит точка с координатами
1)(-4;-800) 2) (-4; 800) 3) (-4; 200) 4) (-4; -200)
Прямая у =5х-1 пересекает параболу у =2х2
1)в одной точке 2) в двух точках
3)в трех точках 4) не пересекает -
12 слайд
Вариант -2.
1. При каком значении аргумента х значение функции у= — 0,25 х2 равно -4 ?
1)-1 и 1 2) 4 3) — 0,25 и 0,25 4) -4 и 4
2. Графику функции у =80 х2 принадлежит точка с координатами
1)(-5;-200) 2) (-5; 2000) 3) (-5; -2000) 4) (-5; -200)
Прямая у =2х+7 пересекает параболу у =3х2
1)в одной точке 2) в двух точках
3)в трех точках 4) не пересекает -
13 слайд
Ответы
В-1 3,1,4В -2 4,2,2
-
-
15 слайд
О замечательных
свойствах параболы -
-
-
-
19 слайд
Применение
параболы в природе -
-
-
-
-
-
-
-
-
-
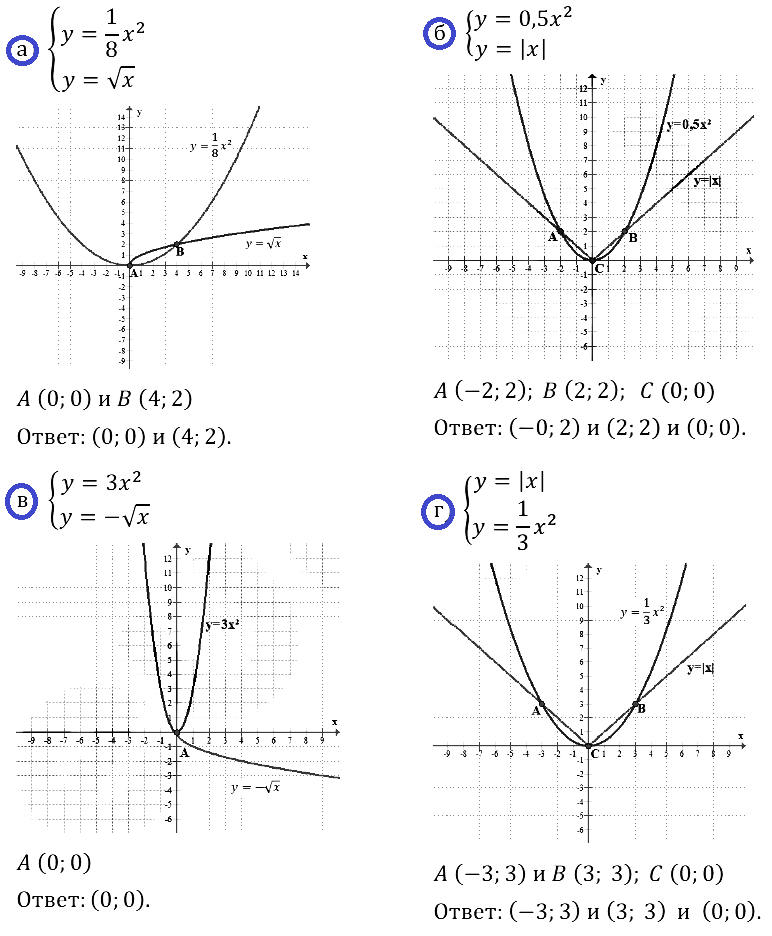
Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). § 19. Функция у = kх2, её свойства и график. ОТВЕТЫ на упражнения 19.1 — 19.66. ГЛАВА 3. Квадратичная функция. Функция у = k/x. Нажмите на спойлер, чтобы посмотреть ответ на задание.
Вернуться в ОГЛАВЛЕНИЕ.
§ 19. Функция у = kх2, её свойства и график
Найдите значение коэффициента k для заданной функции у = kx2:
Задание № 19.1. а) у = 2х2; б) у = –8x2; в) у = 7х2; г) у = –х2.
Смотреть ответы на № 19.1
Задание № 19.2. а) у = 0,2x2; б) у = –x2/8; в) у = –1,85x2; г) у = –x2/37.
Смотреть ответы на № 19.2
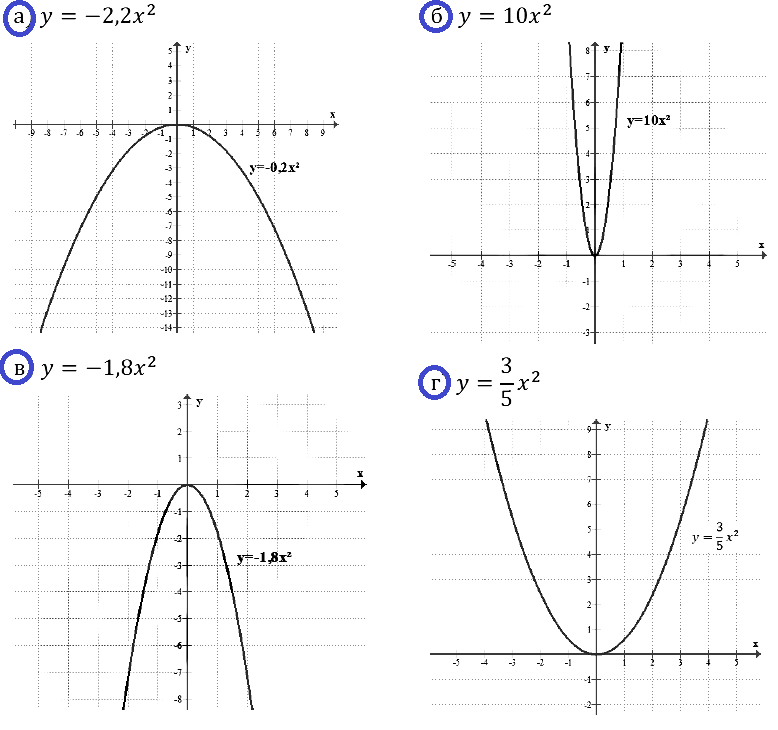
Задание № 19.3. Изобразите схематически график функции:
а) у = –0,2х2; б) у = 10x2; в) г/ = –1,8x2; г) у = 3/5 • x2.
Смотреть ответы на № 19.3
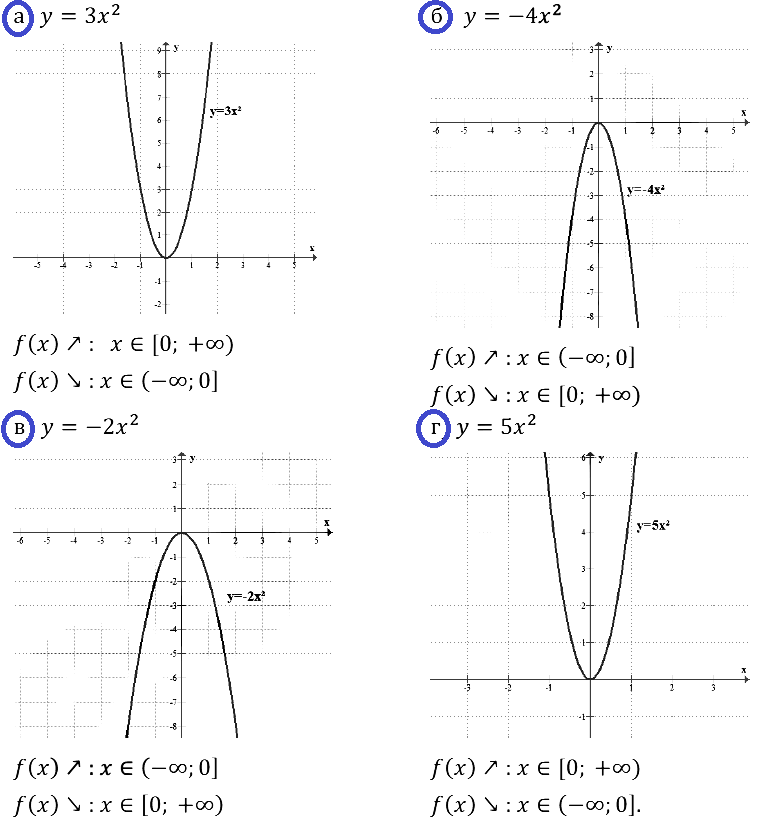
Постройте график функции и укажите, где она убывает, где возрастает:
Задание № 19.4. а) у = 3х2; б) y = –4x2; в) y = –2x2; г) y = 5x2.
Смотреть ответы на № 19.4
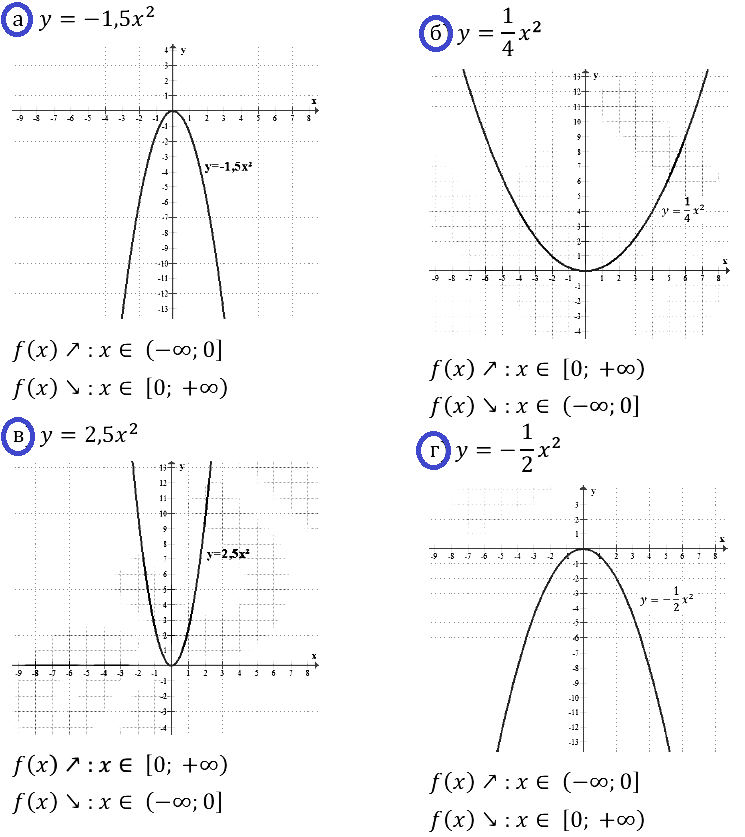
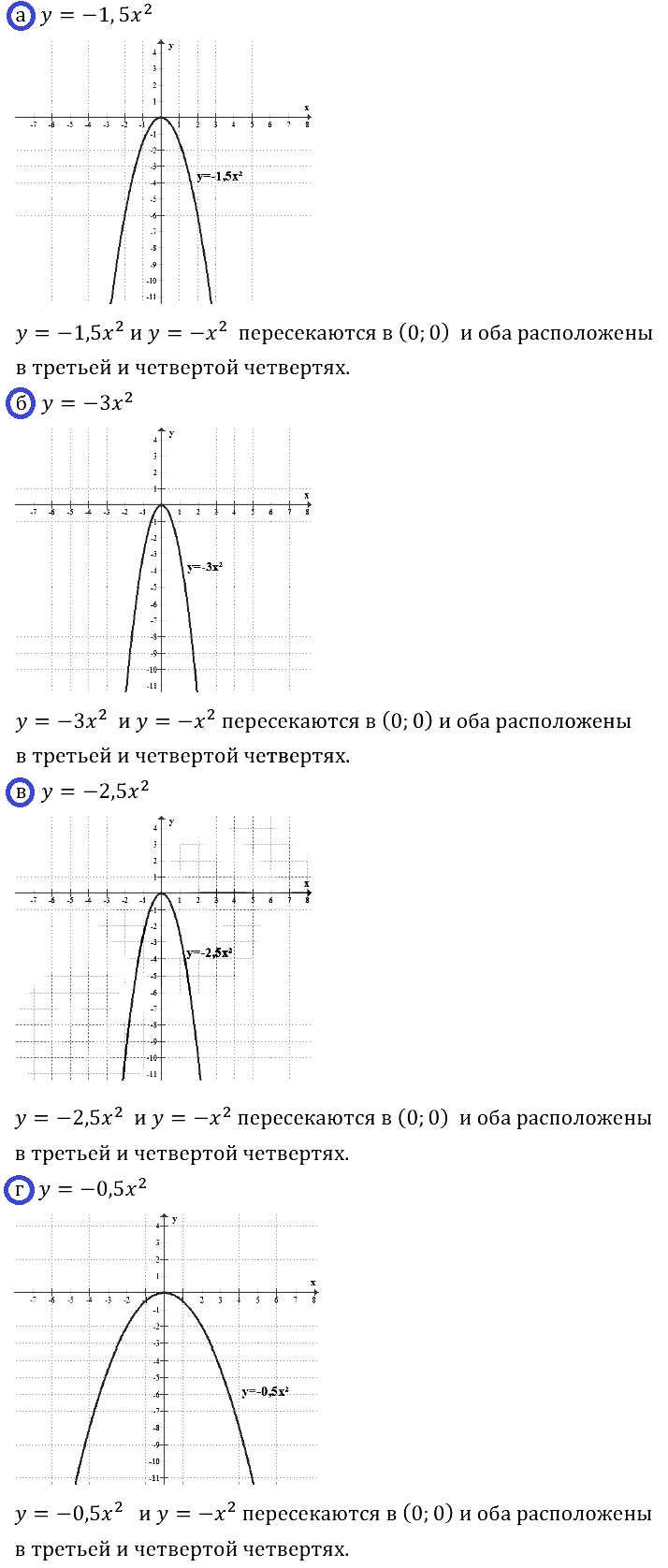
Задание № 19.5. а) у = –1,5x2; б) y = 1/4 • x2; в) y = 2,5x2; г) у = –1/2 • x2.
Смотреть ответы на № 19.5
Постройте в одной системе координат графики заданных функций и сделайте вывод о взаимном расположении построенных графиков:
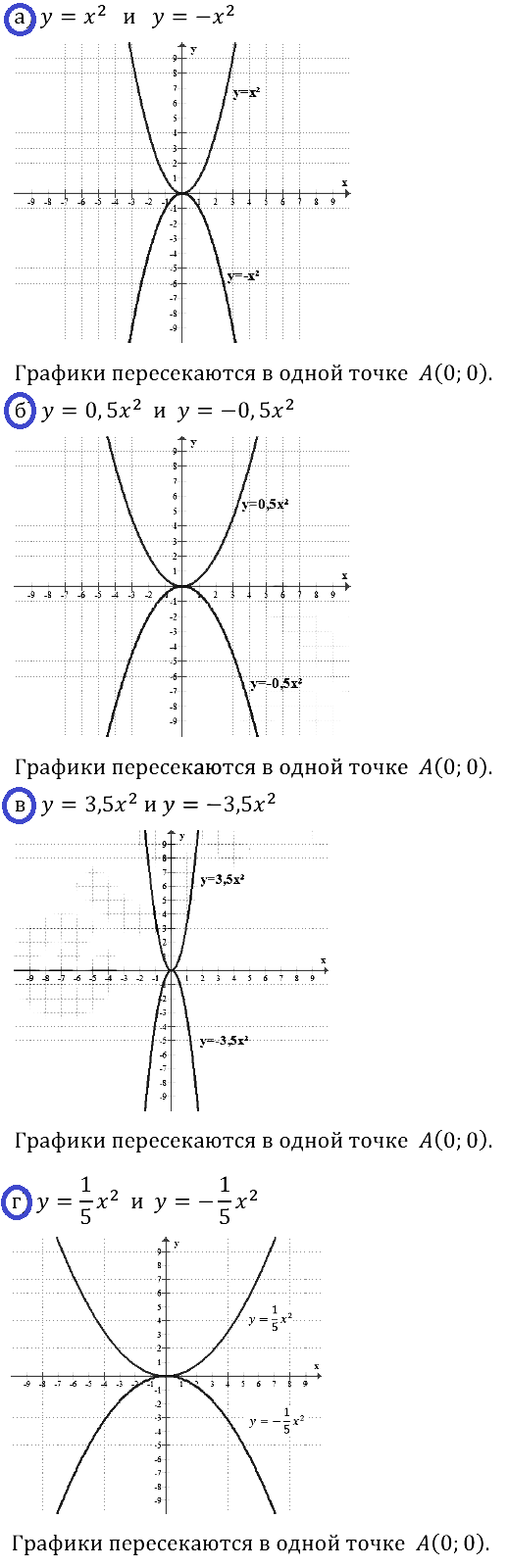
Задание № 19.6. а) у = х2 и у = –х2; б) у = 0,5x2 и y = –0,5x2; в) у = 3,5х2 и у = –3,5х2; г) у = x2/5 и у = –x2/5.
Смотреть ответы на № 19.6
Задание № 19.7.
Смотреть ответы на № 19.7
Задание № 19.8. Не выполняя построения графиков функций, ответьте на вопрос, как расположены в одной системе координат и по отношению друг к другу графики функций: а) у = 105x2 и у = –105x2; б) у = –3,165x2 и у = 3,165x2.
Смотреть ответы на № 19.8
Задание № 19.9. Постройте график функции:
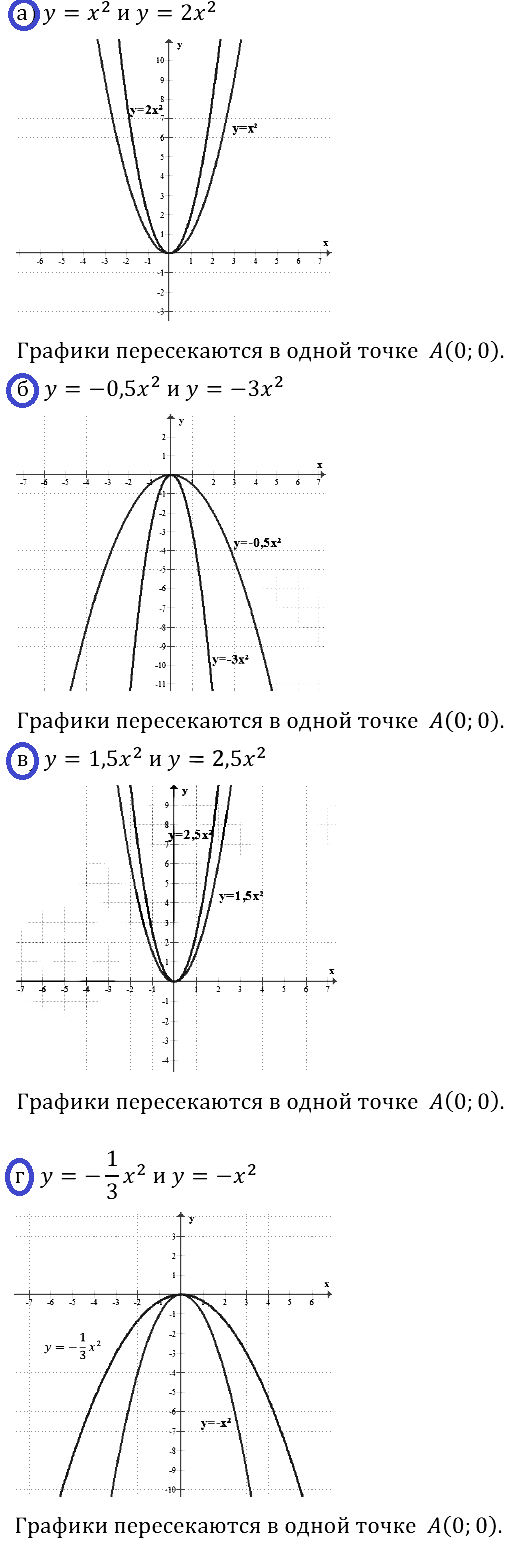
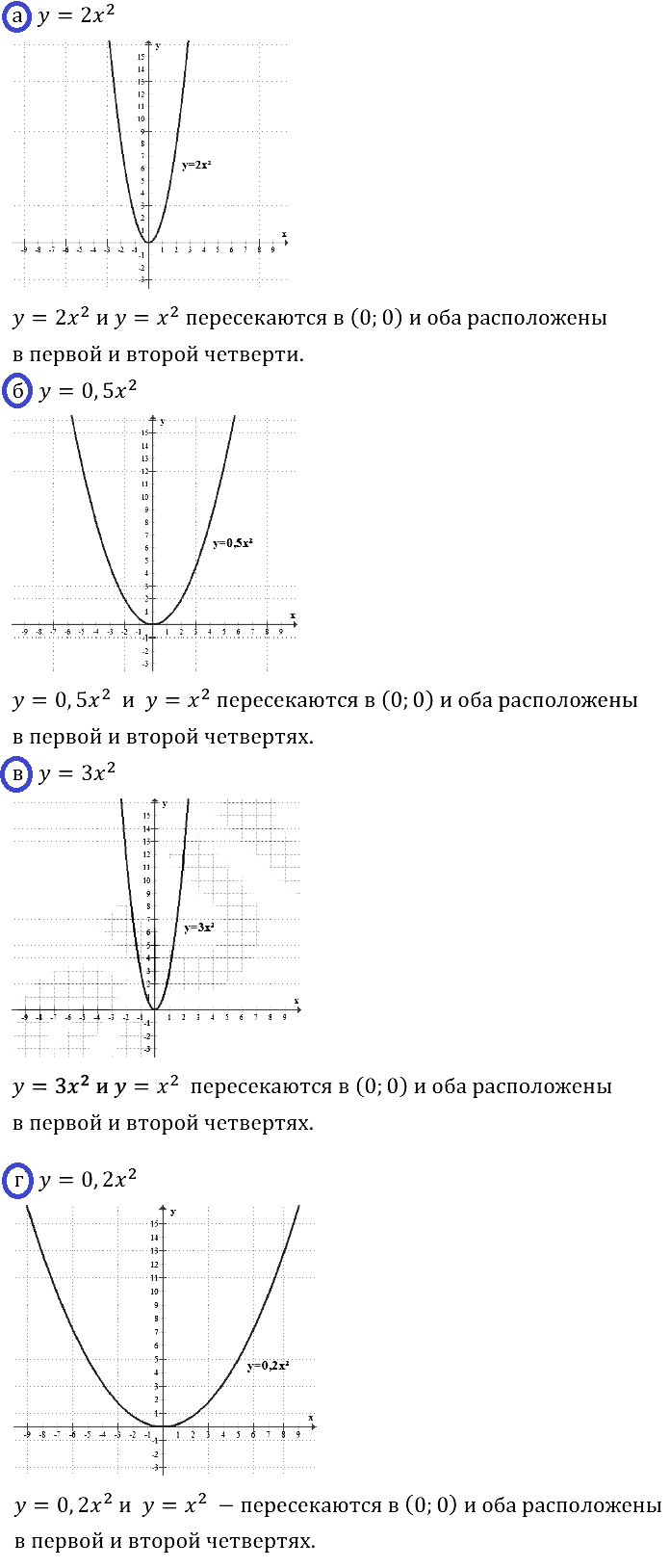
а) у = 2х2; б) y = 0,5х2; в) у = 3х2; г) у = 0,2х2.
Что можно сказать о взаимном расположении построенного графика и графика функции у = х2?
Смотреть ответы на № 19.9
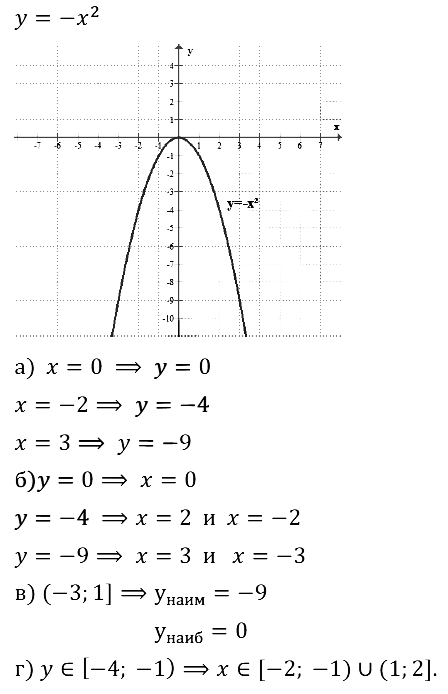
Задание № 19.10. Постройте график функции:
а) у = –1,5х2; б) у = –3х2; в) у = –2,5х2; г) у = –0,5х2.
Что можно сказать о взаимном расположении построенного графика и графика функции у = –х2 ?
Смотреть ответы на № 19.10
Задание № 19.11. Задайте число k так, чтобы график функции у = kx2 был расположен:
а) в первой и второй четвертях;
б) в третьей и четвертой четвертях.
Смотреть ответы на № 19.11
Задание № 19.12.
Смотреть ответы на № 19.12
Задание № 19.13.
Смотреть ответы на № 19.13
Задание № 19.14.
Смотреть ответы на № 19.14
Задание № 19.15.
Смотреть ответы на № 19.15
Задание № 19.16.
Смотреть ответы на № 19.16
Задание № 19.17.
Смотреть ответы на № 19.17
Задание № 19.18.
Смотреть ответы на № 19.18
Задание № 19.19.
Смотреть ответы на № 19.19
Задание № 19.20.
Смотреть ответы на № 19.20
Задание № 19.21.
Смотреть ответы на № 19.21
Задание № 19.22.
Смотреть ответы на № 19.22
Задание № 19.23.
Смотреть ответы на № 19.23
Задание № 19.24.
Смотреть ответы на № 19.24
Задание № 19.25.
Смотреть ответы на № 19.25
Задание № 19.26.
Смотреть ответы на № 19.26
Задание № 19.27.
Смотреть ответы на № 19.27
Задание № 19.28.
Смотреть ответы на № 19.28
Задание № 19.29.
Смотреть ответы на № 19.29
Задание № 19.30.
Смотреть ответы на № 19.30
Задание № 19.31.
Смотреть ответы на № 19.31
Задание № 19.32.
Смотреть ответы на № 19.32
Задание № 19.33.
Смотреть ответы на № 19.33
Задание № 19.34.
Смотреть ответы на № 19.34
Задание № 19.35.
Смотреть ответы на № 19.35
Задание № 19.36.
Смотреть ответы на № 19.36
Задание № 19.37.
Смотреть ответы на № 19.37
Задание № 19.38.
Смотреть ответы на № 19.38
Задание № 19.39.
Смотреть ответы на № 19.39
Задание № 19.40.
Смотреть ответы на № 19.40
Задание № 19.41.
Смотреть ответы на № 19.41
Задание № 19.42.
Смотреть ответы на № 19.42
Задание № 19.43.
Смотреть ответы на № 19.43
Задание № 19.44.
Смотреть ответы на № 19.44
Задание № 19.45.
Смотреть ответы на № 19.45
Задание № 19.46.
Смотреть ответы на № 19.46
Задание № 19.47.
Смотреть ответы на № 19.47
Задание № 19.48.
Смотреть ответы на № 19.48
Задание № 19.49.
Смотреть ответы на № 19.49
Задание № 19.50.
Смотреть ответы на № 19.50
Задание № 19.51.
Смотреть ответы на № 19.51
Задание № 19.52.
Смотреть ответы на № 19.52
Задание № 19.53.
Смотреть ответы на № 19.53
Задание № 19.54.
Смотреть ответы на № 19.54
Задание № 19.55.
Смотреть ответы на № 19.55
Задание № 19.56.
Смотреть ответы на № 19.56
Задание № 19.57.
Смотреть ответы на № 19.57
Задание № 19.58.
Смотреть ответы на № 19.58
Задание № 19.59.
Смотреть ответы на № 19.59
Задание № 19.60.
Смотреть ответы на № 19.60
Задание № 19.61.
Смотреть ответы на № 19.61
Задание № 19.62.
Смотреть ответы на № 19.62
Задание № 19.63.
Смотреть ответы на № 19.63
Задание № 19.64.
Смотреть ответы на № 19.64
Задание № 19.65.
Смотреть ответы на № 19.65
Задание № 19.66.
Смотреть ответы на № 19.66
Вы смотрели: Алгебра 8 класс. Часть 2 (Задачник) УМК Мордкович (2018-2020). ГЛАВА 3. Квадратичная функция. Функция у = k/x. § 19. Функция у = kх2, её свойства и график. ОТВЕТЫ на упражнения 19.1 — 19.66. Вернуться в ОГЛАВЛЕНИЕ.
Просмотров: 77 217