Как найти ускорение — определение и формулы расчета в физике
Содержание:
-
Что такое ускорение
- Единица измерения
-
Как рассчитать ускорение: формулы
- Для прямолинейного движения
- Для равноускоренного движения
- Для равнозамедленного движения
- Нахождение ускорения через массу и силу
- Мгновенное ускорение
- Максимальное ускорение
- Среднее ускорение
- Проекция ускорения
Что такое ускорение
Ускорение (overrightarrow а) — векторная величина в физике, характеризующая быстроту изменения скорости тела.
Ускорение является векторной величиной, показывающей, на сколько изменяется вектор скорости тела при его движении за единицу времени.
Единица измерения
В СИ (системе интернациональной) ускорение измеряется: ( begin{bmatrix}aend{bmatrix}=frac м{с^2})
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Как рассчитать ускорение: формулы
Для прямолинейного движения
Прямолинейное движение — механическое движение, при котором траектория тела — прямая линия.
В этом случае ускорение находится по следующим формулам:
(a;=;frac{mathrm V}t)
(a;=;frac{2S}{t^2})
(a;=;frac{V^2}{2S})
Где (a) — достигнутое ускорение тела, (S) — пройденный путь (расстояние), (t) — затраченное время.
Время отсчитывается от начала движения тела.
При прямолинейном равномерном движении ускорение по модулю равняется нулю.
Для равноускоренного движения
Равноускоренное движение — прямолинейное движение с постоянным положительным ускорением (разгон).
При таком виде движения ускорение определяется по формуле: (a;=;frac{V-V_0}t), где (V_0) и (V) начальная и конечная скорости соответственно, (a) — достигнутое ускорение тела, (t) — затраченное время.
Для равнозамедленного движения
Равнозамедленное движение — прямолинейное движение с постоянным отрицательным ускорением (замедление).
При таком виде движения ускорение находим по формуле: (a;=-;frac{V-V_0}t), где V0 и V начальная и конечная скорости соответственно, a — достигнутое ускорение тела, t — затраченное время.
Нахождение ускорения через массу и силу
Принцип инерции Галилея:
Если не действовать на тело, то его скорость не будет меняться.
Система отсчета (СО) — система координат, точка отсчета и указание начала отсчета времени.
Инерциальная система отсчета (ИСО) — это СО, в которой наблюдается движение по инерции (соблюдается принцип инерции).
II закон Ньютона:
В инерциальных системах отсчёта ускорение, приобретаемое материальной точкой, прямо пропорционально вызывающей его силе, совпадает с ней по направлению и обратно пропорционально массе материальной точки.
или
(overrightarrow a=frac{overrightarrow F}m)
Мгновенное ускорение
Мгновенное ускорение тела (материальной точки) в данный момент времени — это физическая величина, равная пределу, к которому стремится среднее ускорение при стремлении промежутка времени к нулю. Другими словами — это ускорение, которое развивает тело за максимально короткий отрезок времени.
Выражается по формуле:
( overrightarrow a=lim_{trightarrow0}frac{triangleoverrightarrow V}{triangle t})
Максимальное ускорение
(a_{max}=omega v_{max},) где (a_{max}) — максимальное ускорение, (omega) — круговая (угловая, циклическая) частота, (v_{max}) — максимальная скорость.
Среднее ускорение
Среднее ускорение — это отношение изменения скорости к промежутку времени, за который это изменение произошло.
(overrightarrow{a_{ср}}=frac{triangleoverrightarrow V}{triangle t}), где (overrightarrow{a_{ср}}) — среднее ускорение, (triangleoverrightarrow V) — изменение скорости, ( triangle t) — изменение времени.
Проекция ускорения
Определение проекции ускорения на ось (х):
(a_x=frac{V_x-V_{0x}}t), где где (a_x) — проекция ускорения на ось (х), (V_x) — проекция текущей скорости на ось (х), (V_{0x}) — проекция начальной скорости на ось (х), (t) или (triangle t) — промежуток времени, за который произошло изменение проекции скорости.
Насколько полезной была для вас статья?
Рейтинг: 1.92 (Голосов: 36)
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Поиск по содержимому
Виталий Викторович Карабут
Эксперт по предмету «Физика»
Задать вопрос автору статьи
Ускорение: сущность и виды
Под действием различных физических сил тела ускоряют или замедляют свое движение.
Определение 1
Ускорением называют интенсивность изменения скорости движения. Оно характеризует изменение скорости за единицу времени.
В системе СИ ускорение измеряется в метрах в секунду за секунду, иными словами, в метрах в секунду в квадрате ($м/с^2$).
Движение с ускорением, вектор которого не меняется по модулю и направлению, называется равноускоренным.
Определить ускорение при равноускоренном прямолинейном движении можно по формуле:
$a = frac{v_1 — v_0}{t} = frac{Delta v}{t}$,
где $v_1, v_0$ — скорости в начале и в конце рассматриваемого периода времени длительностью $t$.
Отношение изменения скорости к промежутку времени, за который произошло это изменение, называют средним ускорением:
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
$vec{a} = frac{vec{v_1} — vec{v_0}}{t} = frac{Delta vec{v}}{t}$,
В отличие от равноускоренного, здесь имеют значение направления векторов.
Если начальная скорость больше конечной, происходит замедление, которое в физике также принято называть ускорением, но выраженным с отрицательным знаком.
Мгновенное ускорение — ускорение, развиваемое за очень малый промежуток времени (его длительность стремится к нулю):
$vec{a} = limlimits_{t to 0}frac{Delta vec{v}}{Delta t}$.
Ускорение при движении по окружности
Поскольку ускорение — векторная величина, при движении отличном от прямолинейного оно не остается неизменным даже если модуль скорости не изменяется. В связи с этим ускорение вычисляется из начальной и конечной скоростей по правилам векторной математики, т.е. с учетом изменения направления.
Тело, движущееся по окружности, удобно рассматривать как обладающее двумя ускорениями: тангенциальным ($a_{tau}$), направленным по касательной к траектории, и центростремительным, направленным к центру ($a_n$). При равномерном движении по окружности тангенциальное ускорение, отражающее мгновенную скорость тела, может быть равно нулю, но центростремительное имеет место даже в этом случае. Поэтому любое движение по криволинейной траектории является движением с ускорением.
«Формулы ускорения в физике» 👇
Замечание 1
Центростремительное ускорение называется также нормальным, тангенциальное — касательным.
Касательное ускорение определяется как мгновенное при движении на очень малое угловое расстояние, когда длина дуги и длина хорды между начальной и конечной точками малоразличимы (сравниваются мгновенные скорости в этих точках).
Формула для определения центростремительного ускорения:
$a_n = frac{v^2}{R}$,
где $v$ — мгновенная скорость, $R$ — радиус траектории.
При движении по искривленной траектории величину результирующего ускорения получают из тангенциального и нормального исходя из теоремы Пифагора:
$vec{a}^2 = vec{a_{tau}}^2 + vec{a_n}^2 implies vec{a} = sqrt{vec{a_{tau}}^2 + vec{a_n}^2}$
Такое ускорение называется полным.
Пример 1
Найти ускорение тела, разгоняющегося за 10 с от 5 до 100 км/ч.
В начальный момент времени тело двигалось со скоростью
$v_{0} = frac{5000}{3600} approx 1,39 м/с.$
Скорость в конце интервала:
$v_{1} = frac{100000}{3600} approx 27,8 м/с.$
Подставив числовые значения в формулу, получаем:
$a = frac{v_1 — v_0}{t}$
$a = frac{27,8 — 1,39}{10} approx 2,64 м/с^{2}$
Ответ: ускорение составило $ 2,64 м/с^{2}$
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Искать «а» ради «ускорения»-пустое занятие. Искать надо F-Силу,которая вызывает движение,и изменяет его. S/tt=F/m. S,t,m можно измерить. F=?
Ошибка Ньютон: S=att/2. S=att ! (без /2).
«а»-это ЭНЕРГИЯ движения. Она НЕ зависит от графика движения, и численно = S/tt (V/t).
У падающего «яблока..» несколько скоростей: нач. скорость, кон.скорость,средняя скорость, at, 2at. «средняя скорость»-(S/t)-это та-же скорость at,но выраженная через ЭНЕРГИЮ и ВРЕМЯ: F/m*t.
ВСЕ расчёты на движение надо делать ТОЛЬКО из СРЕДНЕЙ скорости! (Энергия одинакова, и НЕ зависит от графика движения). И нет «надобности» в «интегралах». …Задачка: машина m=1165 кг, прошла 250 м. за 18 с.(набрала скорость от 0 до 27,7 м/с за 18 сек.) («Жигули»). Вопрос: какая мощность мотора?
Всякий механизм имеет КПД. КПД ДВС (у бензиновых двс=16%).Решение: S/tt=F/m. 250/324=F/1165, (или 13,9/18=F/1165). F=900 кг.м/сс. Это 12 л.с. при 100% КПД ! При 16% мощность=75 л.с. (а,Да! «ускорение»? оно =0,77 м/сс….). Но и без «а»не обойтись…
Грубая ошибка, находить «а»: Vo=0. V кон.=27,7. t=18 сек. а=(27,7-0)/18. а=1,5 м/сс. Мощность мотора=150 л.с.
То-же с «яблоком…» Vo=0, Vкон.=9,8. t=1 c. Правильно: (0+9,8)/2t. a=4,9 м/cc S=4,9 м.
«Если тело упало на Землю с высоты h, то S/tt ВСЕГДА !!! РАВНО числу 4,9… Это число 4,9 м/сс и ЕСТЬ «УСКОРЕНИЕ СВОБОДНОГО ПАДЕНИЯ»! Скорость: м/с. Ускорение-м/сек.сек. 9,8-это скорость,(но НЕ ускорение).
Сколько ошибок (и слёз) при решении задач:
Vo=5. t=10. a=2. S=? a=? V кон.=?
Решение: S=Vot+att. S=5/10+2*10*10. S=250. a=S/tt. a=2,5. V кон.=Vo+2at. Vкон.=5+2*2*10. V кон.=45. Проверка:S=att. 2,5*10*10=250. S=(v+V)/2*t. (5+45)/2*10. S=250 м.
По принятым формулам: S=(vo+att/2)*t. S=5*10+2*10/10/2=150 м. a=2S/tt. 300/100=3 м/сс
V кон.=v0+at. 5+20=25. S=(5+5+25)*10. S=350 м. («ОГОРОД!»)
Скорость тела может меняться двояко. Она может:
1. увеличиваться;
2. уменьшаться.
Пример:
предположим, что самолёт начинает движение из состояния покоя, поэтому его начальная скорость равна нулю. Самолёт разгоняется, и его скорость постепенно увеличивается. В это время движение самолёта ускоряется.
Приближаясь к цели, пилот самолёта снижает скорость, движение становится всё медленнее и медленнее до остановки самолёта. На этом этапе пути движение замедляется.
Ускорение Замедление
Неравномерное движение может ускоряться или замедляться.
(t) — время движения.
Содержание:
- Определение и формула ускорения
- Единицы измерения ускорения
- Виды ускорения
- Формула ускорения в разных системах координат
- Примеры решения задач
Определение и формула ускорения
Определение
Ускорением (мгновенным ускорением) называют вектор, который определяет быстроту, с которой изменяется скорость
перемещающейся материальной точки.
Обычно ускорение обозначают
$bar{a}$. В теоретической механике встречается обозначение ускорения:
$bar{w}$. Математическим определением мгновенного ускорения являются выражения:
$$bar{a}=frac{d bar{v}}{d t}=dot{bar{v}}(1)$$
где $bar{v}$ – скорость движения материальной точки
или
$$bar{a}=frac{d^{2} bar{r}}{d t^{2}}=ddot{bar{r}}(2)$$
где $bar{r}$ – радиус – вектор, который определяет положение
материальной точки в пространстве.
Вектор ускорения располагается в плоскости соприкосновения, в которой находится главная нормаль и касательная к траектории,
при этом он имеет направление в сторону вогнутости траектории.
Единицы измерения ускорения
Основными единицами измерения ускорения в системе СИ является: [a]=м/с2
в СГС: [a]=см/с2
Виды ускорения
Если построить соприкасающуюся плоскость, в любой точке траектории, то вектор
$bar{a}$ разложим на две взаимно перпендикулярные составляющие:
$$bar{a}=bar{a}_{n}+bar{a}_{tau}(3)$$
где $bar{a}_n$ — вектор, направленный по главной нормали к центру кривизны траектории
материальной точки – это нормальное ускорение; $bar{a}_{tau}$ — вектор, направленный по касательной к траектории –
это касательное ускорение. При этом выполняются равенства:
$$a_{n}=frac{v^{2}}{R}(4)$$
$$a_{tau}=frac{d}{d t}|bar{v}|(5)$$
$$|bar{a}|=a=sqrt{a_{tau}^{2}+a_{n}^{2}}=sqrt{left(frac{v^{2}}{R}right)^{2}+dot{v}^{2}}(6)$$
где $|bar{v}|=v$ – модуль вектора скорости, R – радиус кривизны траектории,
an – проекция вектора
$bar{a}_n$ на направление единичного вектора главной нормали
$(bar{n})$, aт – проекция вектора
$bar{a}_{tau}$ на направление единичного вектора касательной
$left(bar{tau}=frac{bar{v}}{v}right)$. Величина an определяет быстроту изменения направления скорости, а величина
aт — быстроту изменения модуля скорости.
Если $a_{tau}=0$, то такое движение называют равномерным. При
$a_{tau}=$ const движение является равнопеременным (при
$a_{tau} < 0$ равнозамедленным, при
$a_{tau} > 0$ равноускоренным).
Средним ускорением материальной точки
$langlebar{a}rangle$ на отрезке времени от
$t$ до
$t+Delta t$ называется векторная величина, равная отношению:
$$langlebar{a}rangle(t, Delta t)=frac{Delta bar{v}}{Delta t}=frac{bar{v}(t+Delta t)-bar{v}(t)}{Delta t}(7)$$
При $Delta t rightarrow 0$ в пределе среднее ускорение совпадает с мгновенным ускорением:
$$lim _{Delta t rightarrow 0}langlebar{a}rangle(t, Delta t)=lim _{Delta t rightarrow 0} frac{Delta bar{v}}{Delta t}=frac{d bar{v}}{d t}=bar{a}(t)(8)$$
Формула ускорения в разных системах координат
В декартовых координатах проекции ускорения (ax,ay,az) на оси (X,Y,Z)можно представить как:
$$a_{x}=dot{v}_{x}=ddot{x}, quad a_{y}=dot{v}_{y}=ddot{y}, a_{z}=dot{v}_{z}=ddot{z}(9)$$
Соответственно, имеем:
$$bar{a}=ddot{x i}+ddot{y} bar{j}+ddot{z} bar{k}(10)$$
где $bar{i}, bar{j}, bar{k}$ – единичные орты по осям X,Y.Z. При этом модуль ускорения равен:
$$|bar{a}|=a=sqrt{a_{x}^{2}+a_{y}^{2}+a_{z}^{2}}=sqrt{ddot{x}^{2}+ddot{y}^{2}+ddot{z}^{2}}(11)$$
В цилиндрической системе координат имеем:
$$a=sqrt{left(ddot{rho}-rho dot{varphi}^{2}right)^{2}+(rho ddot{varphi}+2 dot{rho} dot{varphi})^{2}+ddot{z}^{2}}(12)$$
В сферической системе координат модуль ускорения можно найти как:
$$
begin{array}{c}
a=left[left(ddot{r}-r dot{varphi}^{2} sin ^{2} theta-r dot{theta}^{2}right)^{2}+(2 dot{r} dot{varphi} sin theta+r ddot{varphi} sin theta+2 r dot{theta} dot{varphi} cos theta)^{2}right. \
+left(2 dot{r} dot{theta} sin theta+r ddot{theta}-2 r dot{varphi}^{2} sin theta cos thetaright)^{2} frac{1}{2}(13)
end{array}
$$
Примеры решения задач
Пример
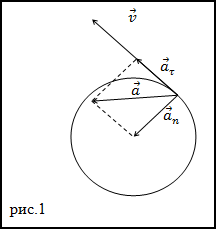
Задание. Материальная точка движется по окружности (рис.1), которая имеет радиус
R=2м, уравнение движения: $S=10 t-2,5 t^{2}$, где t в секундах, а S
в метрах. Каков модуль ускорения данной точки при t=3 c?
Решение. В качестве основы для решения задачи используем формулу:
$$|bar{a}|=a=sqrt{a_{tau}^{2}+a_{n}^{2}}=sqrt{left(frac{v^{2}}{R}right)^{2}+dot{v}^{2}}(1.1)$$
Используя заданное уравнение движения, найдем модуль скорости материальной точки:
$$v(t)=frac{d S}{d t}=10-5 t$$
Продифференцировав уравнение для модуля скорости (1.2) по времени получим тангенциальную составляющую ускорения:
$a_{tau}=-5$ м/с2
Для вычисления нормальной составляющей скорости движения нашей материальной точки следует, используя выражение (1.2) найти:
$a_{n}=frac{v^{2}(t=3)}{R}=frac{(10-5 cdot 3)^{2}}{2}=12,5$ м/с2
Используя выражение (1.1) вычислим искомое ускорение:
$a=sqrt{(-5)^{2}+(12,5)^{2}} approx 13,5$ м/с2
Ответ. $a=approx 13,5$ м/с2

236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 430 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Какова зависимость ускорения материальной точки от времени (a(t)), если частица перемещается по
оси X и ее скорость изменяется в соответствии с уравнением:
$v=alpha sqrt{x}$, где
$alpha$ – постоянная большая нуля? В начальный момент
времени (при t=0 с) материальная точка находилась в начале координат (x=0 м). Нарисуйте график a(t).
Решение. Из условий задачи можно записать, что:
$$v=v_{x}=alpha sqrt{x}=frac{d x}{d t}(2.1)$$
Используя формулу (2.1) найдем зависимость координаты xот времени (x(t) ):
$$int alpha d t=int frac{d x}{sqrt{x}} rightarrow alpha t=2 sqrt{x}+C(2.2)$$
где постоянную интегрирования найдем из начального условия задачи. Мы знаем, что x(0)=0, значит C=0. Имеем:
$$x(t)=frac{1}{4} alpha^{2} t^{2}(2.3)$$
Используя формулу для нахождения ускорения для нашего случая (движение по оси X):
$$a=a_{x}=ddot{x}(2.4)$$
получим искомое выражение для a(t):
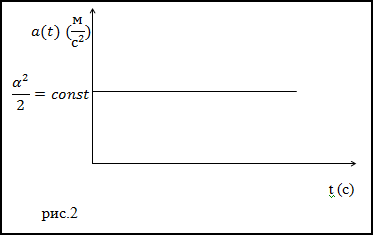
$$a(t)=frac{alpha^{2}}{2}$$
Ответ. $a(t)=frac{alpha^{2}}{2}$ ускорение от времени не зависит, значит, график a(t) принимает вид (рис.2).
Читать дальше: Формула давления.