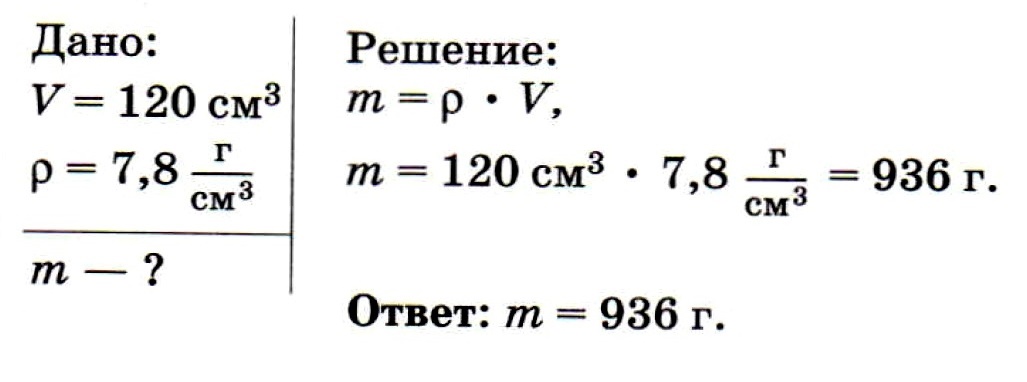18.09.2018Рубрика: Материалы и технологииАвтор: Александр 0
26 953
Для строителя важным навыком является умение посчитать количество леса в кубических метрах или рассчитать площадь поверхности, зная только объем пиломатериала. Разберем сколько кубов в одном брусе 100х150х6000 и используем приведенную ниже методологию расчета.
Содержание
- Показатели, влияющие на расчеты
- Расчеты для бруса 100 на 150 мм
- Итоговые результаты
Показатели, влияющие на расчеты
Длина досок может значительно отличаться. Для струганных досок характерны размеры от 1,5 до 3 м. Что касается обрезной и необрезной доски или бруса, то обычная длина составляет 6 м.
Еще одним важным параметром дерева является сорт. Он может быть первым, вторым, третьим, четвертым или пятым. Наиболее востребованными для стройки является первый (ровные резы, отсутствие обзолов и грибка, а так же трещин) или второй сорт (возможны колебания длины до 10%, наличие грибковых окрасов)
Расчеты для бруса 100 на 150 мм
Размер доски выбирается исходя из строительной задачи. Следует помнить, что стороны пиломатериала формулируется в миллиметрах. Например, брус 100х150х6000 мм.
Для корректного вычисления необходимо перевести миллиметры в метры.
| Характеристики | Обозначение | Миллиметры | Метры |
|---|---|---|---|
| Толщина | H | 100 | 0,1 |
| Ширина | B | 150 | 0,15 |
| Длина | L | 6000 | 6,0 |
| Объем | V | – | – |
Для расчета количества кубов в одном брусе, можно использовать следующую формулу:
- V(объем)=h(толщина) *b(ширина)*L(длина).
V=0,15 x 0,1 x 6,0 = 0,09 кбм
Получается, что объем одного бруска 100х150х6000 мм составляет 0,09 м3.
Теперь, зная V пиломатериала можно определить сколько штук в одном кубе
Для этого используем следующую формулу:
N = V/V(мат.)
- N – штуки
- V – количество кубов
- V(мат.) – объем бруса/доски
N = 1/0,09 = 11,1
Количество бруса 100х150х6000 в одном кубе составляет 11 штук.
Теперь давайте посчитаем сколько метров в одном кубе и какую площадь можно укрыть этим материалом.
Для этого нам необходимо умножить количество брусков в кубе на площадь:
S = N*S1
S1= b*L = 0,1*6 = 0,6 кв.м.
S= 11*0,6 =6,6 кв.м.
Один кубический метр материала 100х150х6000мм состоит из 6,6 квадратных метров покрываемой площади.
Итоговые результаты
Наши расчеты дали следующие результаты:
| Размер | Количество | Площадь | Объем |
|---|---|---|---|
| 100х150х6000 | 11 шт | 6,6 м.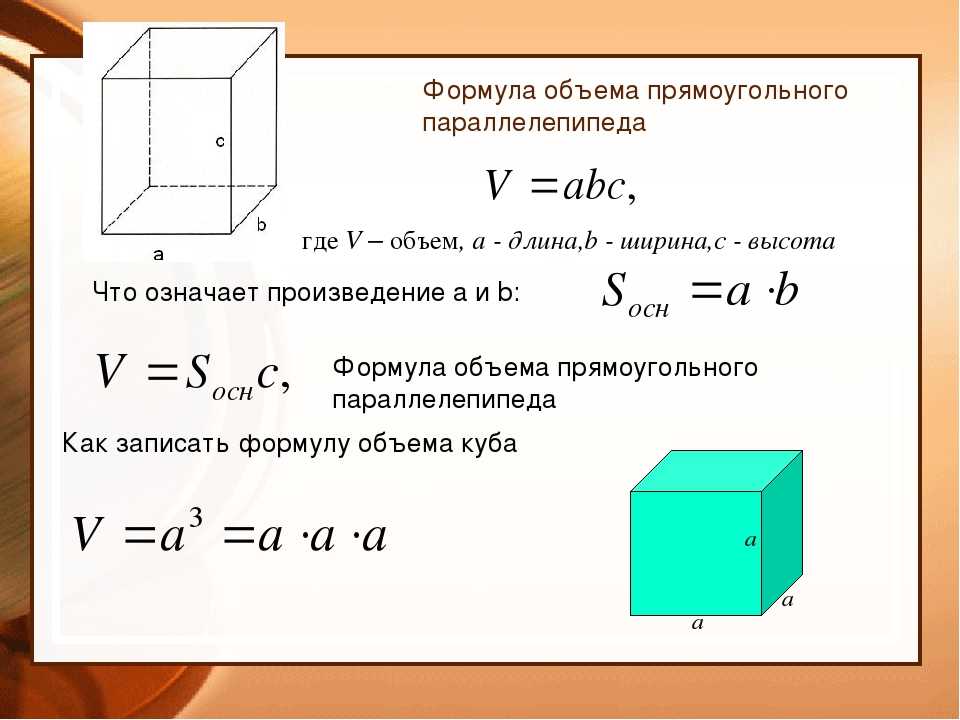 кв. кв. |
0,09 м3 |
По приведенному выше алгоритму можно посчитать объем и площадь для любого обрезного пиломатериала. Нужно только подставить свои значения.
Материал необходимо заказывать с небольшим запасом, лучше всего покупать брус с запасом не менее 7% от объема. Это позволит сэкономить на доставке материалов.
видео-инструкция по расчету своими руками, как рассчитать кубическую площадь, вес, таблица количества, цена, фото
Статьи
Российские застройщики в последнее время при строительстве индивидуальных объектов используют обычный или профилированный брус, осуществляя возведение непосредственно своими руками. Однако многие из них не знают, как посчитать количество материала для будущего строения, а это необходимо делать на этапе составления сметы.
На фото демонстрируется обычный брус.
Мера объема
В первую очередь необходимо знать, как рассчитать брус в кубах, так как именно в них измеряется объем приобретаемых пиломатериалов.
Количество штук
Чтобы понять, сколько единиц материала в одном кубометре, нужно провести достаточно простые вычисления. Количество в кубе бруса удастся определить, если известны полностью все размеры.
В нашем случае приводятся вычисления для элементов с габаритами 200x150x6000 мм.
Объем бруса находится по представленной формуле.
- На начальном этапе исходные параметры должны быть переведены в метры. Таким образом, получится: 0,2×0,15×6 м;
- Теперь необходимо определить объем одного элемента, то есть нужно перемножить представленные данные: 0,2*0,15*6=0,18 куб.м;
- Остается один кубометр разделить на результат предыдущего пункта. В итоге получается такой пример: 1/0,18≈5,55 штук.
Примечание!
Точно по такому же принципу производятся вычисления для элементов с другим сечением и длиной.С уменьшением этих параметров количество единиц будет только увеличиваться.
Для упрощения предварительных расчетов индивидуальным застройщикам может пригодиться специальная таблица количества бруса в кубе. С ее помощью удастся достаточно быстро определить итоговый результат. Нужно лишь взглянуть на основные размеры балок.
Наглядный пример для определения объема одного элемента.
| Габариты | Штук |
| 200x200x6000 | 4,16 |
| 200x150x6000 | 5,5 |
| 150x150x6000 | 7,4 |
| 200x100x6000 | 8,3 |
| 150x100x6000 | 11,1 |
| 100x100x6000 | 16,6 |
Внимание!
В случае необходимости может использоваться специальный калькулятор бруса в кубе, который позволяет произвести вычисления очень быстро.Достаточно ввести исходные данные.
Количество квадратов
Многие не знают, как рассчитать кубическую площадь бруса, а это необходимо для определения квадратуры застройки.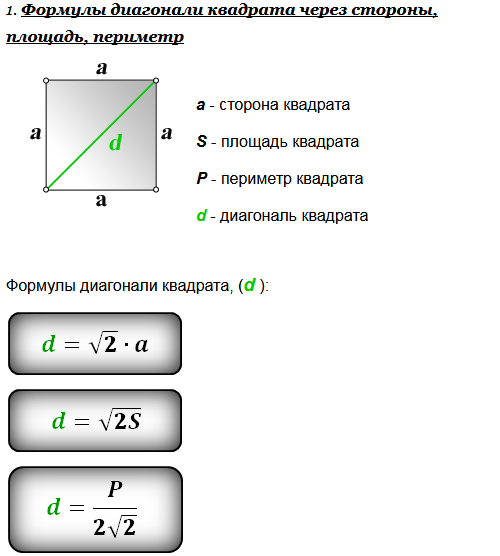
Порядок действий должен быть примерно такой.
Таблица с различными показателями.
- Первым делом измеряется толщина основных элементов. В данном примере она составляет 200 мм;
- Теперь полученное значение из миллиметров переводится непосредственно в метры: 0,2 м;
- На последней стадии кубическая единица делится на результат, который был получен в результате второго действия: 1/0,2=5 кв. м.
Уточнение!
Таким образом, из одного кубометра материала можно возвести 5 квадратных метров стен.Теперь даже начинающий мастер сможет понять, как расчитать кубическую площадь бруса.
Вычисления на примере
При составлении сметы необходимо максимально точно определить объем основного материала, так как цена его достаточно высока. Если приобрести большое количество элементов, то значительная часть останется, что приведет к лишним расходам.
В связи с этим вычислениям нужно уделить особое внимание. В нашей ситуации все расчеты приводятся для строения 6×4 м с высотой деревянных стен 3 м. Внутри имеется четырехметровая перегородка.
При работах будет применяться брус 100x100x6000 мм.
Примерный план будущего строения.
- Сразу же необходимо определить площадь внешних стен. Для этого нужно рассчитать квадратуру каждой плоскости, после чего сложить полученные результаты: (6*3+4*3)*2=60 кв.м;
- К полученному числу необходимо прибавить площадь перегородки. Ее квадратура определяется по той же самой формуле. В итоге должен получиться приблизительно такой пример: 4*3+60=72 кв.м;
- Теперь необходимо понять, сколько квадратов стен удастся построить с использованием одного кубометра материала. Толщина бруса составляет 100 мм, поэтому получается: 1/0,1=10 кв.м;
- На завершающей стадии можно определить количество кубометров материала, которое потребуется для проведения работ.
Общая площадь застройки делится на результат предыдущего пункта: 72/10=7,2 куб. м.
Дополнение!
При проведении расчетов следует учитывать площадь, которую займут оконные и дверные проемы.
В некоторых ситуациях их квадратура может быть достаточно велика.
Масса материала
Вес куба бруса может существенно варьироваться в зависимости от породы древесины и относительной влажности. Ознакомиться с основными показателями можно, если взглянуть на представленную ниже таблицу. В ней учитываются различные факторы, которые влияют на массу материала.
Представлен брус из лиственницы.
| Породы | Вес кубометра в килограммах при различной влажности | |||
| >45% | 23-45% | 18-22% | 10-17% | |
| Дуб, ясень, бук | 1000 | 800 | 750 | 700 |
| Ель, пихта, липа | 800 | 550 | 500 | 450 |
| Лиственница | 900 | 700 | 650 | 600 |
| Сосна, осина | 800 | 600 | 550 | 500 |
Важно!
К первой категории влажности относится свежесрубленная древесина, поэтому она имеет наибольшую массу.
Однако строения обычно возводятся из бруса, который прошел естественную или технологическую сушку.
В качестве заключения
Выше была представлена специальная инструкция, предназначенная для начинающих мастеров, которые не знают, как высчитать количество материала в виде бруса для строительства индивидуального объекта. Правильные вычисления помогут сэкономить денежные средства и избавят от лишних сложностей. Что касается дополнительных сведений по данной теме, то изучить их можно, если ознакомиться с видео в этой статье.
Калькулятор момента инерции двутавровой балки
Калькулятор момента инерции двутавровой балки для расчета второго момента площади (момент инерции) двутавровой балки, модуля сечения, радиуса вращения, площади поперечного сечения и центра масс.
Двутавровая балка представляет собой тип балки
часто используется в фермах в зданиях. Двутавровая балка обычно изготавливается из
конструкционные стали методами горячей и холодной прокатки или сварки. Верхняя и нижняя пластины двутавровой балки называются полками, а вертикальная пластина, соединяющая полки, называется стенкой. На рынке существуют двутавровые балки различных размеров, которые могут быть поставлены поставщиками балок. Благодаря своей форме двутавровая балка обладает высоким моментом инерции и жесткостью, что делает ее устойчивой к изгибающим моментам. Сеть обеспечивает устойчивость против сил сдвига. Эти балки не устойчивы к нагрузкам при кручении (скручиванию) и не должны использоваться в тех случаях, когда преобладает кручение.
| Система единиц (быстрый выбор) | ||
| ВХОДНЫЕ ПАРАМЕТРЫ | ||
| Параметр | Значение | |
| Высота внутренней поверхности фланца [H] | ||
| Ширина [В] | ||
| Толщина фланца [h] | ||
| Толщина стенки [b] | ||
| Длина [л] | ||
93 кгфунтов
94
| РЕЗУЛЬТАТЫ | ||
| Параметр | Значение | |
| Площадь поперечного сечения [A] |
— 92 |
|
| Масса [м] | — | |
| Второй момент площади [I xx ] | — | |
| Второй момент площади [I yy ] | — | |
| Модуль упругости [S xx ] | — | мм^3см^3дюйма^3фута^3 |
| Модуль упругости сечения [S yy ] | — | |
| Радиус вращения [r x ] | — | |
| Радиус вращения [r y ] | — | |
| Расстояние до центра тяжести в направлении x [x c ] | — | |
| Расстояние до центра тяжести в направлении Y [y c ] | — |
Примечание.
Радиус вращения (площадь):
расстояние от оси, на котором площадь тела можно считать равной
сосредоточена, а площадь второго момента этой конфигурации равна
площадь второго момента фактического тела относительно той же оси.
Модуль сечения: Момент
инерция площади поперечного сечения элемента конструкции, деленная на
расстояние от центра тяжести до самой дальней точки сечения; а
мера прочности балки на изгиб.
Момент инерции площади — типичные поперечные сечения I
Момент инерции площади или Момент инерции площади — , также известный как Второй момент площади — I , представляет собой свойство формы, которое используется для прогнозирования прогиба, изгиба и напряжения в балках.
Area Moment of Inertia — Imperial units
- inches 4
Area Moment of Inertia — Metric units
- mm 4
- cm 4
- м 4
Converting between Units
- 1 cm 4 = 10 -8 m 4 = 10 4 mm 4
- 1 in 4 = 4.16×10 5 mm 4 = 41,6 см 4
Пример — преобразование между площадью инертными единицами
9240 CM 4 77 может быть обратно 9240 CM 4 3 .0276 10 4
(9240 см 4 ) 10 4 = 9,24 10 7 ММ 4
9013
. Область)
Для изгиба вокруг оси x можно выразить как
I x = ∫ y 2 DA (1)
, где
I x = зона
I x = Область
9202 Инерция относительно оси x ( m 4 , mm 4 , inches 4 )
y = the perpendicular distance from axis x to the element dA (m, mm, inches )
DA = Элементная область ( M 2 , мм 2 , дюйма 2 ) 48 2 ).
I y = ∫ x 2 dA (2)
where
I y = Area Moment of Inertia related to the y axis ( m 4 , mm 4 , inches 4 )
x = the perpendicular distance from axis y to the element dA (m, mm, inches )
Момент инерции площади для типичных сечений I
- Момент инерции площади для типовых сечений II
Сплошное квадратное сечение
Момент инерции площади для сплошного квадратного сечения можно рассчитать как
I x = A 4 /12 (2)
, где
A = сторона (мм, м, в …)
0002 I y = A 4 /12 (2B)
Сплошная прямоугольная сечение
МОМЕНТ ИНЕРИИ для прямоугольной секции может быть рассчитана как
I x = B x = b x z = b x z = b x = b x z x z x z x z x z x z x = b 3 /12 (3)
, где
B = ширина
H = высота
I Y
I Y 0113 = B 3 H/ 12 (3B)
Сплошная круговая сечение
Момент инерции площади для твердой цилиндрической секции может быть рассчитана как
I x = π r 4 I x = π r 4 I x = π r 4 I x = π r 4 I x = π r 4 I x = / 4
= π D 4 /64 (4)
, где
R = радиус
D = Диаметр
0202
I y = π r 4 / 4
= π d 4 / 64 (4b)
Hollow Cylindrical Cross Section
The Area Moment of Inertia for a Полый цилиндрический сечение можно рассчитать как
I x = π (D O 4 — D I 4 ) / 64 (5)
, где ) / 64 (5)
, где 03
d o = cylinder outside diameter
d i = cylinder inside diameter
I y = π (d o 4 — d i 4 ) / 64 (5b)
Квадратное сечение – диагональные моменты
Моменты инерции площади по диагонали для квадратного сечения можно рассчитать как
30112 x
= I y = a 4 / 12 (6)
Прямоугольное сечение – Моменты площади на любой линии, проходящей через центр тяжести
8 рассчитываться как
I x = (B H / 12) (H 2 COS 2 A + B 2 SIN 2 A) (7)
112444424442444244244424442442444274427442744274427442744424427442н.
Расчёт количества и площади брусков, досок и бруса по объёму
Что может калькулятор ?
Просчитывает количество пиломатериалов(бруски, брус, доски) по заданному объёму.
Рассчитывает требуемое количество пиломатериалов для одного квадратного метра(например для половой доски или бруса для стен).
Отображает количество изделий в кубе.
Может рассчитывать неограниченное количество изделий.
Вся рассчитанная информация доступна для скачивания в формате pdf.
Инструкции
Площадь рассчитывается по ширине изделия.
Одновременно вы можете просчитать неограниченное количество изделий нажав на кнопку «Добавить изделие».
Ширина, толщина и длина указывается в миллиметрах, только целые числа.
К примеру если у вас отображается 22,2 шт и длина была указана 2000 мм то у вас получится 22 доски по 2000мм и одна доска (2000/10)*2 = 400мм.
Как считает калькулятор.
Пример: Дано 10м3 досок шириной 150мм толщиной 50мм и длиной 6000мм.
Объём одной доски — 150мм * 0,001 * 50мм * 0,001 * 6000мм * 0,001 = 0,045м3
Количество досок в 10м3 — 10м3 / 0,045м3 = 222,2шт
Количество досок в кубе — 1м3 / 0,045м3 = 22,2шт
Площадь одной доски — 150мм * 0,001 * 6000мм * 0,001 = 0,9м2
Количество досок в метре квадратном — 1м2 / 0,9м2 = 1,111111шт
1
Первый слайд презентации
Площадь поверхности
прямоугольного
параллелепипеда
5 класс
Подготовила: учитель математики
МБОУ «СШ № 19»
а. Новая Адыгея Тахтамукайского района
Республики Адыгея
ПАНЕШ Бэла Заурбиевна
Изображение слайда
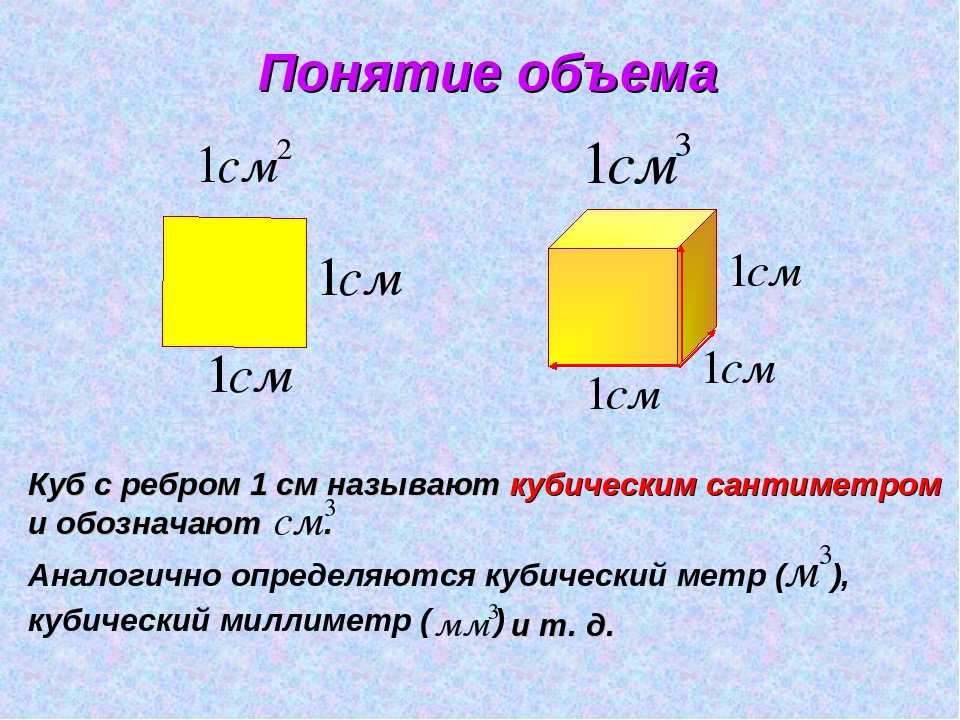
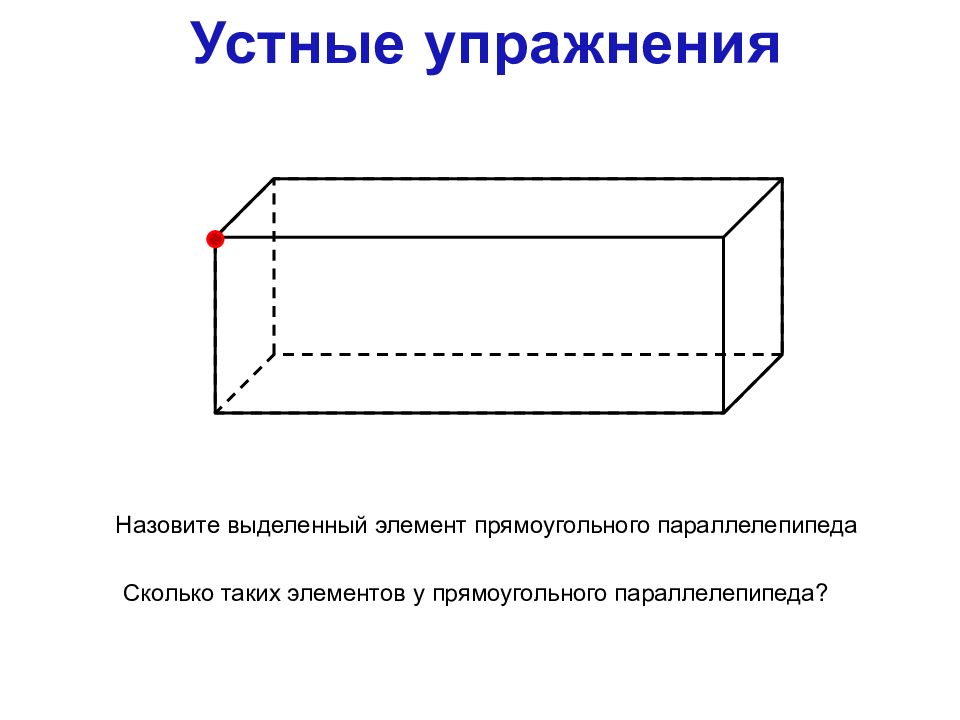
Устные упражнения
Назовите выделенный элемент прямоугольного параллелепипеда
Сколько таких элементов у прямоугольного параллелепипеда?
Изображение слайда
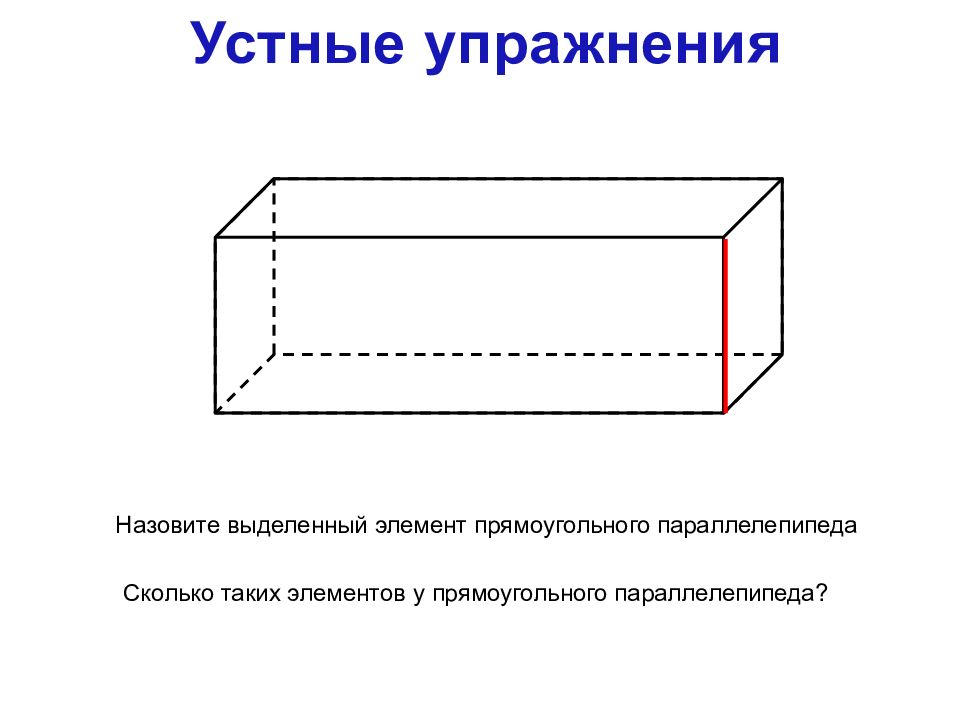
Устные упражнения
Назовите выделенный элемент прямоугольного параллелепипеда
Сколько таких элементов у прямоугольного параллелепипеда?
Изображение слайда
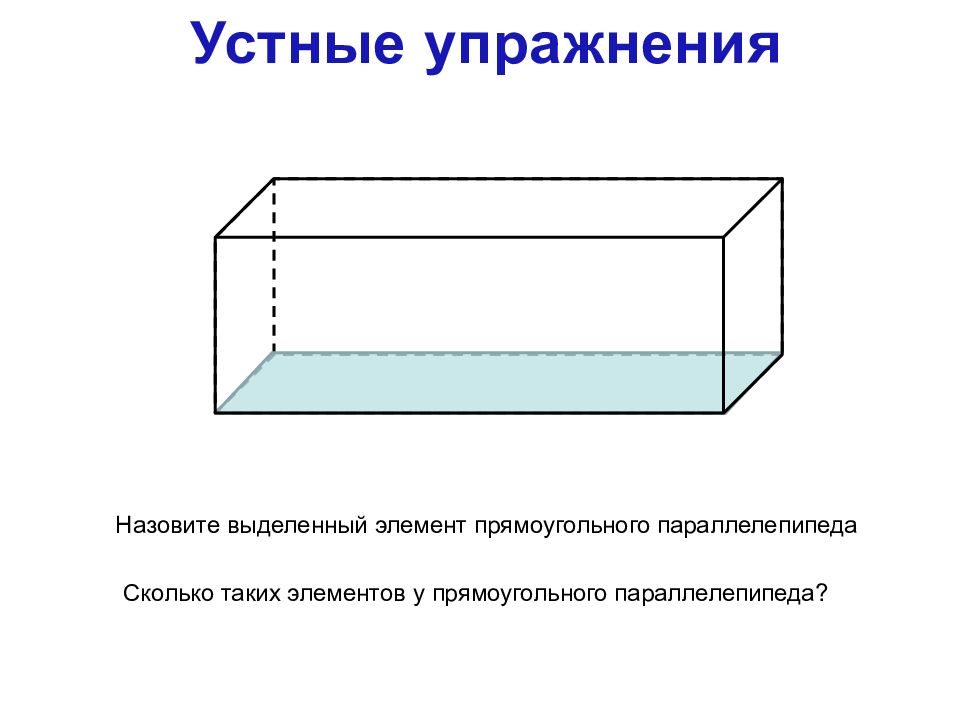
Устные упражнения
Назовите выделенный элемент прямоугольного параллелепипеда
Сколько таких элементов у прямоугольного параллелепипеда?
Изображение слайда
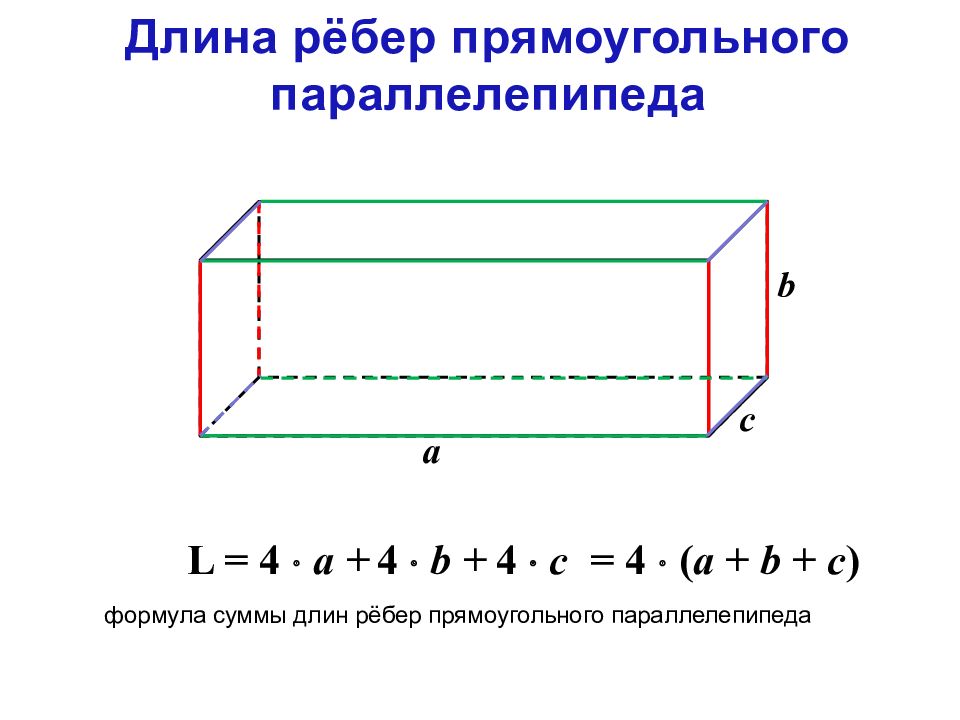
Длина рёбер прямоугольного
параллелепипеда
а
b
c
L = 4 a +
4 b +
4 c
формула суммы длин рёбер прямоугольного параллелепипеда
= 4 ( a + b + c )
Изображение слайда
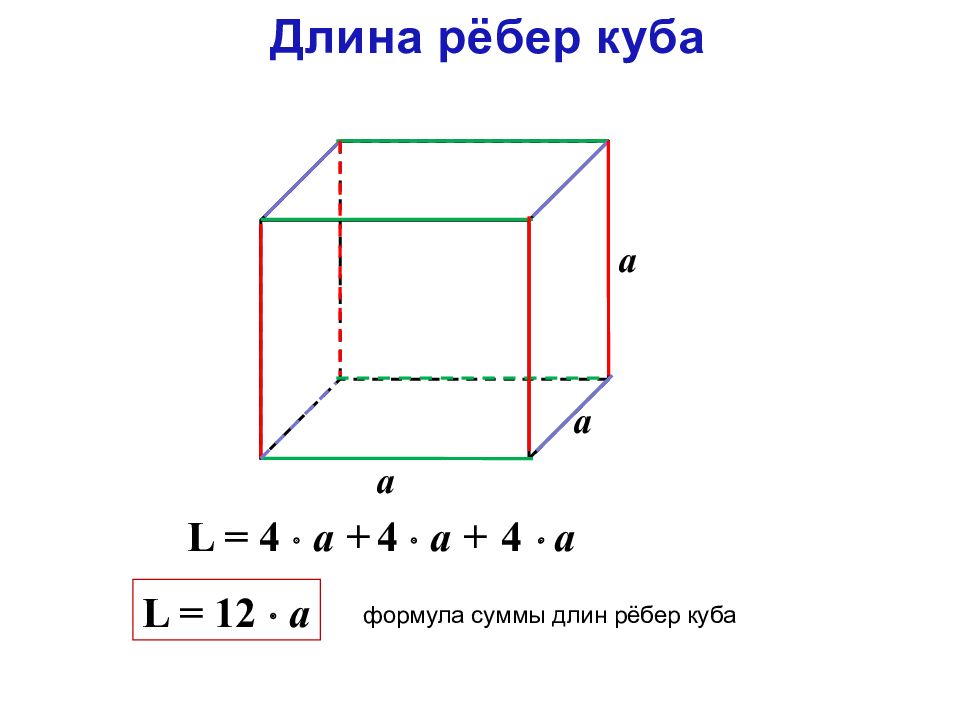
Длина рёбер куба
а
а
а
формула суммы длин рёбер куба
L = 12 a
L = 4 a +
4 а +
4 а
Изображение слайда
Поверхность прямоугольного
параллелепипеда
а
b
c
S = 2 a c +
2 b c +
2 a b
формула площади поверхности прямоугольного параллелепипеда
S = 2 ( a b + b c + a c )
Изображение слайда
Поверхность куба
а
а
а
формула площади поверхности куба
S = 6 a 2
S = 2 a а +
2 а а +
2 a а
Изображение слайда
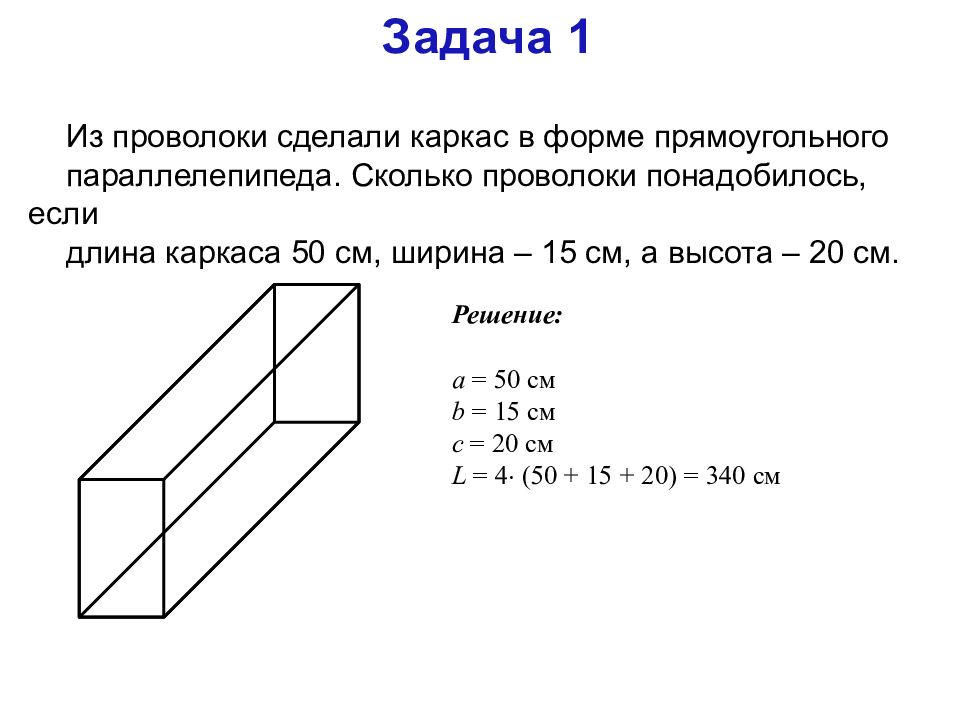
Задача 1
Из проволоки сделали каркас в форме прямоугольного
параллелепипеда. Сколько проволоки понадобилось, если
длина каркаса 50 см, ширина – 15 см, а высота – 20 см.
Решение:
a = 50 см
b = 15 см
c = 20 см
L = 4 ( 50 + 1 5 + 20 ) = 340 см
Изображение слайда
Задача 2
Деревянный брус имеет форму прямоугольного
параллелепипеда. Длина бруса 1 м, ширина – 1 дм,
высота – 7 см. Найдите площадь поверхности
этого бруса.
Решение:
1 м = 100 см
1 дм = 10 см
a = 100 см
b = 10 см
c = 7 см
S = 2 ( 10 100+10 7+100 7 ) =3540 см 2
Изображение слайда
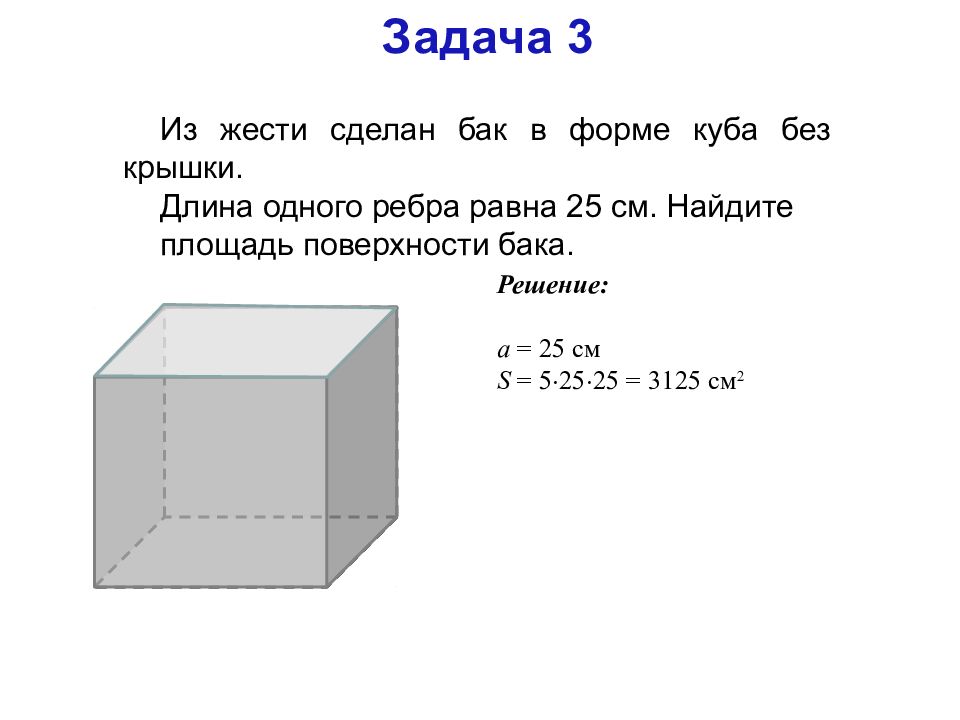
Задача 3
Из жести сделан бак в форме куба без крышки.
Длина одного ребра равна 25 см. Найдите
площадь поверхности бака.
Решение:
a = 25 см
S = 5 2525 = 3125 см 2
Изображение слайда
12
Последний слайд презентации: Площадь поверхности
прямоугольного
параллелепипеда
5 класс
Подготовила: учитель
Самостоятельная работа
№ 795
№ 794
Домашнее задание
№ 813
№ 814
№ 817 (б)
Изображение слайда
Из условия задачи известно, что нам задан брус со сторонами a = 40 см, b = 30 см, c = 20 см. Нужно найти сколько понадобится краски чтобы покрасить поверхность бруса. Если известно, что для покраски 1 квадратного дециметра поверхности нужно 2 гр. краски.
Решать задачу будем следующий образом
- определимся, форму какой геометрической фигуры имеет заданный брус;
- вспомним формулу для нахождения площади поверхности параллелограмма;
- выразим площадь поверхности в квадратных дециметрах;
- найдем нужное количество краски для покраски бруса.
Найдем площадь поверхности бруса
Наш брус имеет форму прямоугольного параллелепипеда.
Площадь прямоугольного параллелепипеда равна сумме площадей его боковых граней и оснований.
Площади оснований параллелограмма равны между собой, так же как и площади передних и боковых граней.
В буквенном виде мы модем записать площадь основания параллелограмма: S = a * b; площадь передней грани S = a * c; площадь боковой грани S = b * c.
Не забываем что каждой грани в параллелепипеде по две.
Запишем формулу для нахождения площади бруса (параллелепипеда):
S = 2(a * b + a * c + b * c);
Вычислим ее:
S = 2(40 * 30 + 40 * 20 + 30 * 20) = 2(1200 + 800 + 600) = 2 * 2600 = 5200 см^2
Переведем квадратные сантиметры в квадратные дециметры.
5200 см^2 : 100 = 52 дм^2.
Вычислим нужное количество краски для покраски бруса
Известно, что расход краски 2 г/дм^2. Умножив площадь бруса на расход краски на 1 дециметр квадратный мы найдем нужное количество краски для покраски нашего бруса.
52 дм^2 * 2 г/дм^2 = 104 г.
Ответ: 104 г.
Определение площади и объема в физике с примером
Содержание:
Определение площади и объема:
В повседневной жизни нам довольно часто приходится иметь дело с определением таких величин, как площадь и объем. Представьте себе, что вам необходимо сделать ремонт в квартире (или доме): побелить стены и потолок, покрасить пол. Чтобы закупить необходимое количество материалов, нужно определить площадь поверхностей и объем краски.
Из уроков математики вам известно, как находить площадь некоторых фи-гур: квадрата, прямоугольника, параллелограмма.
Рис. 6.1.
Рис. 6.2.
Рис. 6.3
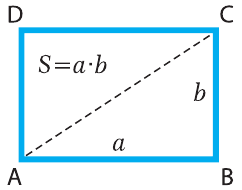
Площадь прямоугольника ABCD (рис. 6.1) вычисляется по формуле:
S = a · b, (6.1)
где a – ширина прямоугольника, b – высота.
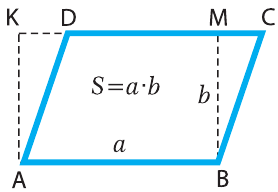
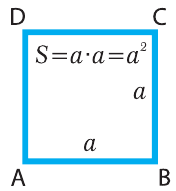
Площадь параллелограмма ABCD (рис. 6.2) также находится по формуле 6.1. Площадь квадрата найти легко, поскольку его ширина и высота одинаковы:
S = a · a = a 2 , (6.2)
Из рис. 6.1 видно, что площадь прямоугольного треугольника АBC можно найти по формуле:
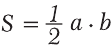
Проблема определения площади круга была решена еще в Древней Греции. Для этого нужно знать радиус круга и число «пи», приблизительное значение
которого π ≈ 3,14.
Площадь круга равняется
S = π · R 2 , (6.4) .
Значение числа 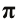
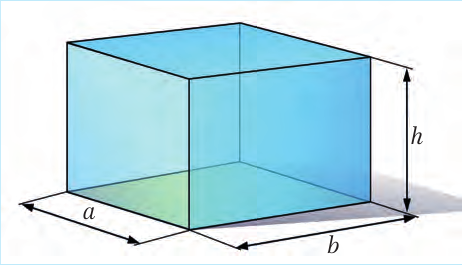
Вычисление объема простых фигур
Каждое тело занимает определенный объем. Чем большую часть пространства занимает тело, тем больше его объем. Объем обозначают буквой V (от volume – объем). Чтобы найти объем прямоугольного бруска или ящика (математики называют эту геометрическую фигуру параллелепипедом) со сторона-ми a, b и h, надо их перемножить (рис. 6.4):
Рис. 6.4.
Рис. 6.5.
V = a · b · h (6.4)
Поскольку S = a · b,
где S – это площадь основания ящика, то формулу (6.4) можно переписать и так:
V = S · h (6.5)
У куба все ребра равны, потому его объем равняется:
V = a · a · a = a 3 (6.6)
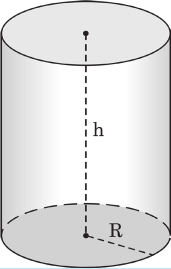
Объем цилиндра (рис. 6.5) с радиусом основания R и высотой h можно также определить по формуле (6.5), то есть:
V = S · h = πR 2 · h (6.7)
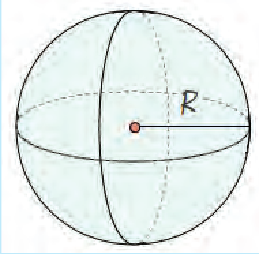
Объем шара (рис. 6.6)
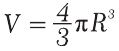
Единицы измерения объема
Поскольку длину сторон измеряют в единицах длины (метр, дециметр, сантиметр и т. д.), то единицы измерения объема – это единицы длины, возведенные в третью степень.
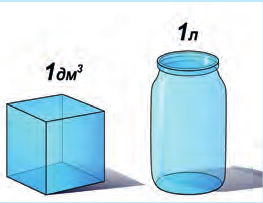
Куб с ребром 1 м имеет объем 1 м 3 (один кубический метр). Один литр (1 л) по определению – это объем куба с ребром 1 дм (рис. 6.7), то есть 1 л = 1 дм 3 (дециметр кубический). Один литр равен 1000 кубических сантиметров: 1 л = 1000 см 3 . Объем в один сантиметр кубический еще называют миллилитром, то есть тысячной частью литра (1 мл = 0,001 л).
Рис. 6.7. Один литр – это 1дм 3
Напомним, что дециметр – это десятая часть метра, а сантиметр – сотая часть метра
Таблица 6.1
| 1 м 3 = 1 000 л | 1 м 3 = 1 000 000 см 3 |
| 1 л = 1 дм 3 | 1 л = 1000 см 3 |
| 1 дм 3 = 1 000 см 3 | 1 л = 1 000 мл |
| 1 см3 = 1 мл | 1 мл = 0,001 л |
- Заказать решение задач по физике
Измерение объема тел неправильной формы
Прибор для измерения объема называют мензуркой, или мерным цилиндром (рис. 6.8). Мензурка – это прозрачный сосуд с нанесенными делениями, которые обозначают объем в миллилитрах. Дома у вас наверняка есть мерный стакан, то есть та же мензурка. Литровой или поллитровой банкой, или стаканом (250 мл) также можно пользоваться, если не нужна большая точность. С помощью мензурки можно определить объем жидкости и тела неправильной формы. Для этого в мензурку нужно налить воду и определить объем этой воды. Потом полностью погрузить тело в воду и запомнить новое значение объема. Разница измеренных значений равна объему тела.

Рис. 6.8. Деления мензурки определяют объем в миллилитрах (то есть в см 3 )
История:
 |
Существует легенда, согласно которой первым такой способ определения объема изобрел древнегреческий ученый Архимед. Произошло это во время размышлений над довольно сложной зада-чей, предложенной царем Гиероном. Идея решения возникла тогда, когда Архимед влез в ванну и заметил, что уровень воды поднялся. Ученый понял, что вытесненный объем воды как раз равен объему погруженного в нее тела. Восторженный Архимед выпрыгнул из ванны и выбежал на улицу с криком «Эврика! Эврика!», что в переводе с древнегреческого значит «На-шел! Нашел!». |
Итоги:
- Площадь тел правильной формы равна произведению основы на высоту и измеряется в квадратных единицах длины S = a · b.
- Объем тел правильной формы определяется как произведение площади основы на высоту и измеряется в кубических единицах V = S · h.
- Объем тел произвольной формы определяют с помощью мензурки
- Площадь круга определяют по формуле S = π · R 2 .
- Объем шара равен
.
| Рекомендую подробно изучить предметы: |
|
| Ещё лекции с примерами решения и объяснением: |
- Связь физики с другими науками
- Макромир, мегамир и микромир в физике
- Пространство и время
- Что изучает механика в физике
- Единая физическая картина мира
- Физика и научно-технический прогресс
- Физические величины и их единицы измерения
- Точность измерений и погрешности
При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org
Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи
Сайт пишется, поддерживается и управляется коллективом преподавателей
Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.
Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.
Как найти площадь бруска физика
Формулы, используемые в задачах по физике на плотность, массу и объем.
Название величины
Обозначение
Единицы измерения
Формула
Масса
m = p * V
Объем
V = m / p
Плотность
кг/м 3
p = m / V
Плотность равна отношению массы тела к его объёму. Плотность обозначают греческой буквой ρ (ро).
Физика 7 класс: все формулы на трех страницах
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Найдите плотность молока, если 206 г молока занимают объем 200 см 3 ?
Задача № 2. Определите объем кирпича, если его масса 5 кг?
Задача № 3. Определите массу стальной детали объёмом 120 см 3
Задача № 4. Размеры двух прямоугольных плиток одинаковы. Какая из них имеет большую массу, если одна плитка чугунная, другая — стальная?
Решение: Из таблицы плотности веществ (см. в конце страницы) определим, что плотность чугуна (ρ2 = 7000 кг/м 3 ) меньше плотности стали (ρ1 = 7800 кг/м 3 ). Следовательно, в единице объема чугуна содержится меньшая масса, чем в единице объема стали, так как чем меньше плотность вещества, тем меньше его масса, если объемы тел одинаковы.
Задача № 5. Определите плотность мела, если масса его куска объемом 20 см 3 равна 48 г. Выразите эту плотность в кг/м 3 и в г/см 3 .
Ответ: Плотность мела 2,4 г/см 3 , или 2400 кг/м 3 .
Задача № 6. Какова масса дубовой балки длиной 5 м и площадью поперечного сечения 0,04 м 2 ?
ОТВЕТ: 160 кг.
РЕШЕНИЕ. Из формулы для плотности получаем m = p • V. С учетом того, что объем балки V = S • l , получаем: m = p • S • l.
Вычисляем: m = 800 кг/м 3 • 0,04 м 2 • 5 м = 160 кг.
Задача № 7. Брусок, масса которого 21,6 г, имеет размеры 4 х 2,5 х 0,8 см. Определить, из какого вещества он сделан.
ОТВЕТ: Брусок сделан из алюминия.
Задача № 8 (повышенной сложности). Полый медный куб с длиной ребра а = 6 см имеет массу m = 810 г. Какова толщина стенок куба?
ОТВЕТ: 5 мм.
РЕШЕНИЕ: Объем кубика VK = а 3 = 216 см 3 . Объем стенок VС можно вычислить, зная массу кубика mК и плотность меди р: VС = mК / р = 91 см 3 . Следовательно, объем полости VП = VK — VC = 125 см 3 . Поскольку 125 см 3 = (5 см) 3 , полость является кубом с длиной ребра b = 5 см. Отсюда следует, что толщина стенок куба равна (а — b)/2 = (6 – 5)/2 = 0,5 см.
Задача № 9 (олимпиадный уровень). Масса пробирки с водой составляет 50 г. Масса этой же пробирки, заполненной водой, но с куском металла в ней массой 12 г составляет 60,5 г. Определите плотность металла, помещенного в пробирку.
ОТВЕТ: 8000 кг/м 3
РЕШЕНИЕ: Если бы часть воды из пробирки не вылилась, то в этом случае общая масса пробирки, воды и куска металла в ней была бы равна 50 г + 12 г = 62 г. По условию задачи масса воды в пробирке с куском металла в ней равна 60,5 г. Следовательно, масса воды, вытесненной металлом, равна 1,5 г, т. е. составляет 1/8 массы куска металла. Таким образом, плотность металла в 8 раз больше плотности воды.
Задачи на плотность, массу и объем с решением. Таблица плотности веществ.
Справочный материал для «Задачи на плотность, массу и объем«
Как, зная только массу, рассчитать плотность?
- Если объем тела (вещества) неизвестен или не задан явно в условиях задачи, то попытайтесь его измерить, вычислить или узнать, используя косвенные (дополнительные) данные.
- Если вещество сыпучее или жидкое, то оно, как правило, находится в емкости, которая обычно имеет стандартный объем. Так, например, объем бочки обычно равен 200 литров, объем ведра – 10 литров, объем стакана – 200 миллилитров (0,2 литра), объем столовой ложки – 20 мл, объем чайной – 5 мл. Об объеме трехлитровых и литровых банок нетрудно догадаться из их названия.
- Если жидкость занимает не всю емкость или емкость нестандартная, то перелейте ее в другую тару, объем которой известен.Если подходящей емкости нет, перелейте жидкость с помощью мерной кружки (банки, бутылки). В процессе вычерпывания жидкости просто посчитайте количество таких кружек и умножьте на объем мерной тары.
- Если тело имеет простую форму, то вычислите его объем, используя соответствующие геометрические формулы. Так, например, если тело имеет форму прямоугольного параллелепипеда, то его объем будет равен произведению длин его ребер. То есть: Vпар. = a • b • c, где Vпар. – объем прямоугольного параллелепипеда, а a, b, c — значения его длины, ширины и высоты (толщины), соответственно.
- Если тело имеет сложную геометрическую форму, то попробуйте (условно!) разбить его на несколько простых частей, найти объем каждой из них отдельно и затем сложить полученные значения.
- Если тело невозможно разделить на более простые фигуры (например, статуэтку), то воспользуйтесь методикой Архимеда. Опустите тело в воду и измерьте объем вытесненной жидкости. Если тело не тонет, то «утопите» его с помощью тонкой палочки (проволоки).
- Если объем вытесненной телом воды посчитать проблематично, то взвесьте вылившуюся воду, или найдите разность между начальной и оставшейся массой воды. При этом, количество килограммов воды будет равняться количеству литров, количество граммов – количеству миллилитров, а количество тонн – количеству кубометров.
Конспект урока «Задачи на плотность, массу и объем с решением».
Расчёт количества и площади брусков, досок и бруса по объёму
Что может калькулятор ?
Просчитывает количество пиломатериалов(бруски, брус, доски) по заданному объёму.
Рассчитывает требуемое количество пиломатериалов для одного квадратного метра(например для половой доски или бруса для стен).
Отображает количество изделий в кубе.
Может рассчитывать неограниченное количество изделий.
Вся рассчитанная информация доступна для скачивания в формате pdf.
Инструкции
Площадь рассчитывается по ширине изделия.
Одновременно вы можете просчитать неограниченное количество изделий нажав на кнопку «Добавить изделие».
Ширина, толщина и длина указывается в миллиметрах, только целые числа.
К примеру если у вас отображается 22,2 шт и длина была указана 2000 мм то у вас получится 22 доски по 2000мм и одна доска (2000/10)*2 = 400мм.
Как считает калькулятор.
Пример: Дано 10м 3 досок шириной 150мм толщиной 50мм и длиной 6000мм.
Объём одной доски — 150мм * 0,001 * 50мм * 0,001 * 6000мм * 0,001 = 0,045м 3
Количество досок в 10м 3 — 10м 3 / 0,045м 3 = 222,2шт
Количество досок в кубе — 1м 3 / 0,045м 3 = 22,2шт
Площадь одной доски — 150мм * 0,001 * 6000мм * 0,001 = 0,9м 2
Количество досок в метре квадратном — 1м 2 / 0,9м 2 = 1,111111шт
источники:
http://uchitel.pro/%D0%B7%D0%B0%D0%B4%D0%B0%D1%87%D0%B8-%D0%BD%D0%B0-%D0%BF%D0%BB%D0%BE%D1%82%D0%BD%D0%BE%D1%81%D1%82%D1%8C/
http://calc-best.ru/stroitelnye/raschyot-pilomaterialov-po-obyomu

 Общая площадь застройки делится на результат предыдущего пункта: 72/10=7,2 куб. м.
Общая площадь застройки делится на результат предыдущего пункта: 72/10=7,2 куб. м.