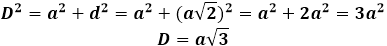Формула как найти диагональ куба если

Куб является базовым геометрическим телом, когда речь заходит об объеме и объемных телах. Недаром третья степень, которая получается умножением трех одинаковых чисел друг на друга (как при нахождении объема куба — трех его измерений одинаковых измерений) названа в его честь.

Основным и единственным параметром куба является его ребро a,так как все ребра у куба конгруэнтны, и представляют собой одновременно и длину, и ширину, и высоту. Соответственно, всего одно значение определяет все возможные характеристики куба, связанные с его измерениями.

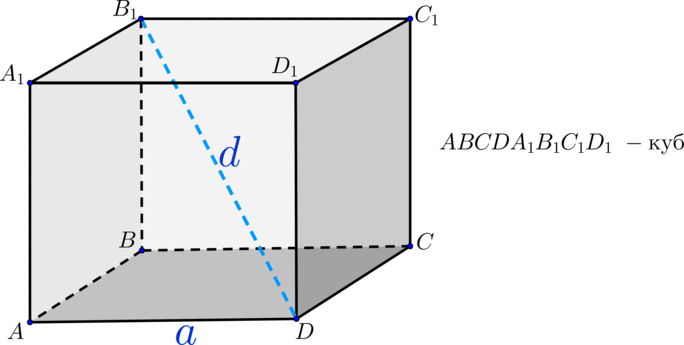
Помимо ребер, вершины куба можно соединить диагоналями. Диагонали могут проходить через грани куба, тогда они будут просто диагональю основания или диагональю квадрата в плоскости, либо диагонали могут быть проведены внутри самого куба, соединяя противоположные основания в крайних точках (вершинах).

Чтобы найти диагональ куба через его ребро, необходимо сначала провести дополнительное построение в виде диагонали одного из соединяемых оснований, тогда диагональ куба станет гипотенузой новоиспеченного прямоугольного треугольника, катетами которого являются ребро куба и диагональ основания. Если ребро куба задано условиями задачи, то диагональ квадрата в основании придется сначала вычислить по формуле:
d=a√2

Тогда диагональ куба можно будет выразить через теорему Пифагора, и она примет следующий вид:

Факт 2.
(bullet) Если сфера вписана в куб (то есть касается всех его граней), то ее радиус равен (0,5a), где (a) – ребро куба.
(bullet) Если сфера описана около куба (то есть все вершины куба лежат на сфере), то ее радиус равен (0,5d), где (d) – диагональ куба.
(bullet) Центр сферы, вписанной в куб или описанной около куба, лежит в точке пересечения диагоналей куба.

A cube is defined as a 3D solid object which has six square faces and all sides equal to each other. It is one of the five platonic solids and is also known as a regular hexahedron. Six square faces, eight vertices, and twelve edges make up the cube. Its length, breadth and height all are same as it is a square with all sides of the same length. The common line between any two faces of a cube is called its edge. It acts as a boundary line between two faces.

Diagonal of a cube

A cube’s diagonal is the line segment connecting any two non-adjacent vertices of the cube. There are two types of cube diagonals, that is, face diagonal and body diagonal. A face diagonal joins two non-adjacent vertices via a single face while a body diagonal does the same by passing through the body of the cube. There are 12 face diagonals and 4 body diagonals possible inside a cube.

Face diagonal formula

Length of face diagonal of cube = √2a

where,

a is the side length of cube.

Body diagonal formula

Length of body diagonal of cube = √3a

where,

a is the side length of cube.

Derivation

Suppose we have a cube with side length a, face diagonal d and body diagonal D.

Now it is known that face diagonal is the hypotenuse of the right triangle it forms with two side lengths. 

So, using Pythagoras theorem we get,

d² = a² + a²

d² = 2a²

d = √2a   …….. (1)

Also, the face diagonal and one side length form a right triangle with body diagonal as hypotenuse.

Again using Pythagoras theorem we get,

D² = a² + d²

Using (1) we get,

D² = a² + (√2a)²

D² = a² + 2a²

D² = 3a²

D = √3a

This derives the formulas for face diagonals and body diagonals of a cube.

Sample Problems

Problem 1. Calculate the face diagonal of a cube of side length 2 m.

Solution:

We have,

a = 2

Using the formula we get,

d = √2a

= √2 (2)

= (1.414) (2)

= 2.83 m

Problem 2. Calculate the face diagonal of a cube of side length 5 m.

Solution:

We have,

a = 5

Using the formula we get,

d = √2a

= √2 (5)

= (1.414) (5)

= 7.07 m

Problem 3. Calculate the body diagonal of a cube of side length 3 m.

Solution:

We have,

a = 3

Using the formula we get,

D = √3a

= √3 (3)

= (1.732) (3)

= 5.196 m

Problem 4. Calculate the body diagonal of a cube of side length 7 m.

Solution:

We have,

a = 7

Using the formula we get,

D = √3a

= √3 (7)

= (1.732) (7)

= 12.12 m

Problem 5. Calculate the side length if the face diagonal of a cube is 6 m.

Solution:

We have,

d = 6

Using the formula we get,

d = √2a

=> a = d/√2

= 6/√2

= 4.24 m

Problem 6. Calculate the side length if the body diagonal of a cube is 13√3 m.

Solution:

We have,

D = 13√3

Using the formula we get,

D = √3a

=> a = D/√3

= 13√3/√3

= 13 m

Problem 7. Calculate the body diagonal of a cube if its face diagonal is 9√2 m.

Solution:

We have,

d = 9√2

Find the side length.

d = √2a

=> a = d/√2

= 9√2/√2

= 9 m

Now using the formula we get,

D = √3a

= √3 (9)

= 15.58 m

Last Updated :
15 May, 2022

Like Article

Save Article

Введите данные:

Достаточно ввести только одно значение, остальное калькулятор посчитает сам.

Округление:

* — обязательно заполнить