MathCAD — это просто! Часть 11. Продолжаем работать с матрицами
Матрицы — вещь важная, а потому было бы просто непростительно отводить на них всего одну статью из нашего цикла о работе в среде MathCAD. Узнав о том, как можно транспонировать матрицы, вычислять определители, обратные матрицы, а также перемножать и складывать их, сегодня мы с вами продолжим издевательства над этими важными в математике объектами. Думаю, что изложенные ниже сведения будут полезны и в практических вычислениях, производимых в среде MathCAD, ведь матрицы очень часто встречаются в реальных задачах.
Еще о вспомогательных функциях
В прошлый раз мы немного поговорили о специальных MathCAD’овских функциях, позволяющих разрезать матрицы на составные части или же склеивать их. Это не единственные из вспомогательных функций, действующих над матрицами, которые могут пригодиться в практике повседневной работы. Пришло время познакомиться с некоторыми другими функциями, которые также имеют неплохой шанс оказаться весьма и весьма полезными. Особую роль в матричном исчислении играют единичные матрицы. На всякий случай напомню, что единичной называется такая матрица, у которой все недиагональные элементы равны нулю, а элементы, расположенные на главной диагонали (от верхнего левого угла к нижнему правому), равны единице. Единичные матрицы могут иметь самые разные размеры. Чтобы пользователь не тратил свое время на вбивание нулей и единиц в строки и столбцы такой матрицы, в MathCAD’е имеется специальная функция Identity, создающая единичную матрицу заданного размера. У этой функции есть единственный аргумент, задающий размерность матрицы.
Еще она по своему действию довольно близкая к Identity функция называется Diag. Она создает не матрицы, а векторы, состоящие из диагональных элементов квадратных матриц (т.е. из тех элементов, которые стоят на ее главной диагонали). Стоит при этом отметить, что размер вектора, получаемого на выходе, автоматически определяется размером входной матрицы.
Для определения размера матриц можно использовать функции Rows и Cols. Каждая из них имеет один-единственный входной параметр, которым является сама матрица, а на выходе выдают значения числа строк и столбцов соответственно. Для определения размера вектора можно использовать функцию length, которая работает аналогично указанным для матриц функциям.
Интересной также является предоставляемая MathCAD’ом функция для сортировки элементов векторов. Называется она просто и незатейливо — Sort. В качестве входного параметра этой функции нужно передать вектор, сортировкой которого мы будем заниматься, и на выходе получим почти такой же вектор, только его элементы будут упорядочены по возрастанию. Для сортировки строк и столбцов матрицы можно воспользоваться соответственно функциями Rsort и Csort, которым нужно передать в качестве параметров саму матрицу и номер того столбца или строки, которые должны быть отсортированы. Правда, работают эти функции несколько загадочно, иногда сортируя не только нужный столбец (строку), но и все остальные (см. соответствующую иллюстрацию). Чтобы изменить порядок следования чисел в векторе или порядок строк в матрице на противоположный, нужно воспользоваться функцией Reverse, в качестве аргумента для которой нужно передать изменяемые матрицу или вектор.
Ранг и норма матрицы
Два фундаментальных понятия, играющих очень важную роль в линейной алгебре — это ранг и норма матрицы. MathCAD позволяет пользователю вычислять эти характеристики матриц без лишних усилий, и сейчас я расскажу, как именно это делается.
Минором матрицы порядка k называется определитель, вычисленный для матрицы, образованной из k столбцов и k строк данной матрицы. Главным минором называется минор, для которого номера выбранных столбцов совпадают с номерами выбранных строк. Понимаю, это определение звучит несколько громоздко, но я думаю, если вы прочитаете его внимательно еще раз, то все станет просто и понятно. Рангом матрицы называется наибольший порядок среди всех ее ненулевых миноров. Ранг матрицы характеризует число линейно независимых столбцов или строк матрицы, а потому в матричной алгебре эта характеристика используется весьма широко. Для вычисления ранга матрицы в MathCAD’е используется функция Rank, которой в качестве аргумента передается та самая матрица, ранг которой нужно вычислить.
Норма матрицы — понятие более расплывчатое, чем ранг. Для полного определения нормы матрицы используется система ограничений, которым должен подчиняться строящийся по определенным правилам функционал. Вы можете найти подробное определение нормы матрицы в любом учебнике по линейной алгебре. Мы же сейчас удовлетворимся знанием того, что норма матрицы — это некоторый аналог величины, который для векторов называют длиной (норма вектора как раз и есть его длина). Впрочем, в отличие от длины вектора, где все понятно и определенно, норма матрицы может вычисляться несколькими разными способами, и в зависимости от способа вычисления ее величина может быть различной. Всем функциям для вычисления нормы матрицы, о которых здесь идет речь, требуется в качестве аргумента передавать ту матрицу, для которой будет вестись вычисление нормы. Функция Norm1 определяет норму путем складывания модулей элементов для каждого из столбцов и выбором наибольшей из получившихся для столбцов сумм. Функция Normi работает аналогичным образом, только для вычисления сумм там используются не столбцы, а строки. Функция Norme вычисляет норму матрицы по тому же алгоритму, по какому вычисляется норма вектора: квадраты всех элементов матрицы суммируются, а затем из полученного числа извлекается корень.
Собственные вектора и собственные значения матриц
Собственным вектором x и собственным значением ? матрицы X называются такие вектор и число соответственно, которые удовлетворяют соотношению xX = ?x. Обычно матрица имеет несколько собственных векторов и соответствующих им собственных значений, а потому мы будем рассматривать именно этот случай. Конечно, в MathCAD’е не слишком сложно с помощью некоторых преобразований рассчитать необходимые числа и вектора самостоятельно, однако можно еще больше упростить себе жизнь, воспользовавшись встроенными в эту среду функциями.
Функция Eigenvecs принимает в качестве входного параметра некоторую матрицу, а возвращает другую, содержащую собственные вектора исходной. При интерпретации результатов работы этой функции необходимо помнить, что в MathCAD’е вектора записываются в виде столбцов, так что и в этой матрице каждый из столбцов является собственным вектором первоначальной матрицы. Другая функция, Eigenvals, также принимает на вход некоторую матрицу, однако выдает для нее уже не собственные вектора, а собственные значения. Записываются они также в виде столбика. В этом столбце они идут в том же порядке, что и столбцы в матрице, возвращаемые первой функцией. То есть i-му столбцу матрицы, получаемой на выходе функцией Eigenvecs, соответствует i-е собственное значение в векторе. Впрочем, проследить соответствие собственных векторов и собственных значений для матрицы можно и более наглядным образом. Для этого существует специальная функция Eigenvec (не путайте с Eigenvecs), которой на вход передаются матрица и одно из ее собственных значений, а она уже вычисляет соответствующий этому собственному значению собственный вектор.
Скалярное и векторное произведение векторов
Напоследок поговорим о вещах довольно простых, но очень распространенных в практике решения задач, а потому особенно важных. Сейчас мы рассмотрим, как с помощью MathCAD’а вычислять скалярное и векторное произведение векторов. Напомню, что скалярным произведением x.y называется число, равное x0y0 + x1y1 + x2y2 + … + xnyn, а вот с векторным все несколько сложнее. Оно определяется только для трехмерных векторов и вычисляется как определитель матрицы, составленной из базисных векторов (i, j и k) и элементов тех векторов, для которых вычисляется векторное произведение. Традиционно в математике векторное произведение обозначают c помощью крестика, который ставится между двумя перемножаемыми векторами.
Для вычисления скалярного и векторного произведения векторов обратимся снова к панели матричных вычислений, неоднократно выручавшей нас в наших упражнениях с MathCAD’ом. Скалярное произведение называется на ней Dot Product и обозначается как точка между двумя векторами, а векторное — Cross Product и обозначается крестиком, как я уже говорил выше. Чтобы перемножить два вектора, вы можете сначала обозначить их с помощью каких- либо символьных обозначений, а можете сразу записывать произведения между столбцами чисел.
Теперь, пожалуй, о матрицах самое основное и важное сказано. Как видите, в плане работы с векторами и матрицами MathCAD ничуть не менее мощный, чем во всем остальном. Поэтому использовать эту среду для матричных вычислений можно и нужно. Ну а как это делать, вы теперь уже знаете.
Компьютерная газета. Статья была опубликована в номере 24 за 2008 год в рубрике soft
Как найти норму вектора в маткаде
Mathcad содержит функции для обычных в линейной алгебре действий с массивами. Эти функции предназначены для использования с векторами и матрицами. Если явно не указано, что функция определена для векторного или матричного аргумента, не следует в ней использовать массивы как аргумент. Обратите внимание, что операторы, которые ожидают в качестве аргумента вектор, всегда ожидают вектор-столбец, а не вектор-строку. Чтобы заменить вектор-строку на вектор-столбец, используйте оператор транспонирования [Ctrl]1.
Если Вы используете Mathcad PLUS, Вы будете также иметь несколько дополнительных функций, определенных для векторов. Эти функции скорее предназначены для анализа данных, чем для действий с матрицами. Они обсуждены в Главе “Встроенные функции”.
Следующие таблицы перечисляют векторные и матричные функции Mathcad. В этих таблицах
- A и B — массивы (векторы или матрицы).
- v — вектор.
- M и N — квадратные матрицы.
- z — скалярное выражение.
- Имена, начинающиеся с букв m, n, i или j — целые числа.
Размеры и диапазон значений массива
В Mathcad есть несколько функций, которые возвращают информацию относительно размеров массива и диапазона его элементов. Рисунок 10 показывает, как эти функции используются.
| Имя функции | Возвращается. |
| rows(A) | Число строк в массиве A. Если А — скаляр, возвращается 0. |
| cols(A) | Число столбцов в массиве A. Если A скаляр, возвращается 0. |
| length(v) | Число элементов в векторе v. |
| last(v) | Индекс последнего элемента в векторе v. |
| max(A) | Самый большой элемент в массиве A. Если A имеет комплексные элементы, возвращает наибольшую вещественную часть плюс i, умноженную на наибольшую мнимую часть. |
| min(A) | Самый маленький элемент в массиве A. Если A имеет комплексные элементы, возвращает наименьшую вещественную часть плюс i, умноженную на наименьшую мнимую часть. |
Рисунок 10: Векторные и матричные функции для нахождения размера массива и получения информации относительно диапазона элементов.
Специальные типы матриц
Можно использовать следующие функции, чтобы произвести от массива или скаляра матрицу специального типа или формы. Функции rref, diag и geninv доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| identity(n) | n x n единичная матрица (матрица, все диагональные элементы которой равны 1, а все остальные элементы равны 0). |
| Re(A) | Массив, состоящий из элементов, которые являются вещественными частями элементов A. |
| Im(A) | Массив, состоящий из элементов, которые являются мнимыми частями элементов A. |
| Е diag(v) | Диагональная матрица, содержащая на диагонали элементы v. |
| Е geninv(A) | Левая обратная к A матрица L такая, что LA = I, где I — единичная матрица, имеющая то же самое число столбцов, что и A. Матрица А — m x n вещественная матрица, где m>=n. |
| Е rref(A) | Ступенчатая форма матрицы A. |
Рисунок 11: Функции для преобразования массивов. Обратите внимание, что функции diag и rref являются доступными только в Mathcad PLUS.
Специальные характеристики матрицы
Можно использовать функции из следующей таблицы, чтобы найти след, ранг, нормы и числа обусловленности матрицы. Кроме tr, все эти функции доступны только в Mathcad PLUS.
| Имя функции | Возвращается. |
| tr(M) | Сумма диагональных элементов, называемая следом M. |
| Е rank(A) | Ранг вещественной матрицы A. |
| Е norm1(M) | L1 норма матрицы M. |
| Е norm2(M) | L2 норма матрицы M. |
| Е norme(M) | Евклидова норма матрицы M. |
| Е normi(M) | Равномерная норма матрицы M. |
| Е cond1(M) | Число обусловленности матрицы M, основанное на L1 норме. |
| Е cond2(M) | Число обусловленности матрицы M, основанное на L2 норме. |
| Е conde(M) | Число обусловленности матрицы M, основанное на евклидовой норме. |
| Е condi (M) | Число обусловленности матрицы M, основанное на равномерной норме. |
Формирование новых матриц из существующих
В Mathcad есть две функции для объединения матриц вместе — бок о бок, или одна над другой. В Mathcad также есть функция для извлечения подматрицы. Рисунки 12 и 13 показывают некоторые примеры.
| Имя функции | Возвращается. |
| augment (A, B) | Массив, сформированный расположением A и B бок о бок. Массивы A и B должны иметь одинаковое число строк. |
| stack (A, B) | Массив, сформированный расположением A над B. Массивы A и B должны иметь одинаковое число столбцов. |
| submatrix (A, ir, jr, ic, jc) | Субматрица, состоящая из всех элементов, содержащихся в строках с ir по jc и столбцах с ic по jc. Чтобы поддерживать порядок строк и-или столбцов, удостоверьтесь, что ir |
Рисунок 12: Объединение матриц функциями stack и augment.
Рисунок 13: Извлечение субматрицы из матрицы при помощи функции submatrix.
Собственные значения и собственные векторы
В Mathcad существуют функции eigenval и eigenvec для нахождения собственных значений и собственных векторов матрицы. В Mathcad PLUS также есть функция eigenvecs для получения всех собственных векторов сразу. Если Вы используете Mathcad PLUS, Вы будете также иметь доступ к genvals и genvecs для нахождения обобщенных собственных значений и собственных векторов. Рисунок 14 показывает, как некоторые из этих функций используются.
Возвращается.
| Имя функции | |
| eigenvals (M) | Вектор, содержащий собственные значения матрицы M. |
| eigenvec (M, z) | Матрица, содержащая нормированный собственный вектор, соответствующий собственному значению z квадратной матрицы M. |
| Е eigenvecs (M) | Матрица, содержащая нормированные собственные векторы, соответствующие собственным значениям квадратной матрицы M. n-ный столбец возвращенной матрицы — собственный вектор, соответствующий n-ному собственному значению, возвращенному eigenvals. |
| Е genvals (M,N) | Вектор v собственных значений, каждое из которых удовлетворяет обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. Вектор x — соответствующий собственный вектор. |
| Е genvecs (M,N) | Матрица, содержащая нормализованные собственные векторы, соответствующие собственным значениям в v, векторе, возвращенном genvals. n-ный столбец этой матрицы — собственный вектор x, удовлетворяющий обобщенной задаче о собственных значениях . Матрицы M и N — вещественнозначные квадратные матрицы одного размера. |
Рисунок 14: Нахождение собственных значений и собственных векторов.
Рисунок 15: Использование eigenvecs для одновременного нахождения всех собственных векторов.
Если Вы используете Mathcad PLUS, Вы будете иметь доступ к некоторым дополнительным функциям для выполнения специальных разложений матрицы: QR, LU, Холесского, и по сингулярным базисам. Некоторые из этих функций возвращают две или три матрицы, соединенные вместе в одну большую матрицу. Используйте submatrix, чтобы извлечь эти две или три меньшие матрицы. Рисунок 16 показывает пример.
| Имя функции | Возвращается. |
| Е cholesky(M) | Нижняя треугольная матрица L такая, что LL T =M. Матрица M должна быть симметричной положительно определенной. Симметрия означает, что M=M T , положительная определённость — что x T Mx>0 для любого вектора x 0. |
| Е qr(A) | Матрица, чьи первые n столбцов содержат ортогональную матрицу Q, а последующие столбцы содержат верхнюю треугольную матрицу R. Матрицы Q и R удовлетворяют равенству A=QR. Матрица A должна быть вещественной. |
| Е lu(M) | Матрица, которая содержит три квадратные матрицы P, L и U, расположенные последовательно в указанном порядке и имеющие с M одинаковый размер. L и U являются соответственно нижней и верхней треугольными матрицами. Эти три матрицы удовлетворяют равенству PM=LU . |
| Е svd(A) | Матрица, содержащая две расположенные друг над другом матрицы U и V. Сверху находится U — размера m x n, снизу V — размера n x n. Матрицы U и V удовлетворяют равенству A=Udiag(s)V T , где s — вектор, возвращенный svds(A). A должна быть вещественнозначной матрицей размера m x n, где m>=n. |
| Е svds(A) | Вектор, содержащий сингулярные значения вещественнозначной матрицы размера m x n, где m>=n. |
Рисунок 16: Использование функции submatrix для извлечения результата из функции rq. Используйте submatrix, чтобы извлечь подобным образом результаты из функций lu и svd. Обратите внимание, что эти функции доступны только в Mathcad PLUS.
Решение линейной системы уравнений
Если Вы используете Mathcad PLUS, Вы сможете использовать функцию lsolve для решения линейной системы уравнений. Рисунок 17 показывает пример. Обратите внимание, что M не может быть ни вырожденной, ни почти вырожденной для использования с lsolve. Матрица называется вырожденной, если её детерминант равен нулю. Матрица почти вырождена, если у неё большое число обусловленности. Можно использовать одну из функций, описанных на странице 204, чтобы найти число обусловленности матрицы.
Возвращается.
| Имя функции | |
| Е lsolve (M, v) | Вектор решения x такой, что Mx=v. |
Если Вы не используете Mathcad PLUS, Вы всё-таки можете решать систему линейных уравнений, используя обращение матрицы, как показано в нижнем правом углу Рисунка 9.
Рисунок 17: Использование lsolve для решения системы из двух уравнений с двумя неизвестными.
Исправляем ошибки: Нашли опечатку? Выделите ее мышкой и нажмите Ctrl+Enter
Как найти норму вектора в маткаде
Глава 3. Работа с векторами и матрицами
3.5 Транспонирование матрицы и вычисление определителя , нормы
Транспонированием называется операция, в результате которой столбцы исходной матрицы становятся строками, а строки – столбцами.
Для реализации этой и последующих операций выполните следующие действия:
– Наберите имя матрицы.
– Щелкните на кнопке со значком матрицы на математической панели.
– На панели Matrix (Матрицы) щелкните мышью на значке соответствующей операции, в данном случае М Т .
При вводе больших векторов из соображений экономии места удобно вводить их в виде строки с последующим транспонированием (рис. 3.8 ).
Транспонирование матрицы Определитель квадратной матрицы
D — неквадратная матрица
Ввод в виде строки
Вывод в виде строки
модуль вещественного числа
модуль комплексного числа
Рис. 3. 8 Транспонирование матрицы и вычисление ее определителя
Все матричные операторы и матричные функции работают только с векторами (в виде столбца), но не со строками, поэтому строки вначале приходится транспонировать в столбец, а после выполнения нужной операции вновь транспонировать в строку.
В MathCAD 12 при преобразовании строки и столбец имена строки и столбца должны быть разными.
Вычисление определителя матрицы
Для нахождения определителя заданной матрицы на панели Matrix выберите значок | X |, имеющий тройное значение:
– вычисление определителя матрицы, если Х – матрица;
– модуль числа, если Х– вещественное или комплексное число;
– длина вектора, если Х – вектор.
MathCAD 13 и 14 не может автоматически, как более старые версии, выбрать нужное действие. Необходимо в контекстном меню указать требуемую операцию.
Норма квадратной матрицы
Норма квадратной матрицы характеризует порядок величины элементов матрицы.
В MathCAD есть 4 функции для оценки нормы (рис. 3.9 ):
– norm 1( A ) – норма в пространстве L 1 ;
– norm 2( A ) – норма в пространстве L 2 ;
– norme(A) – евклидова норма;
– normi ( A ) – max – норма, или – норма.
Евклидова норма эквивалентна длине многомерного вектора .
Как видно на рис.4.12, величина нормы мало зависит от способа ее вычисления. При увеличении всех элементов матрицы в 100 раз все нормы также увеличиваются в 100 раз.
Рис. 3. 9 Функции для вычисления нормы матрицы матрицы
http://old.exponenta.ru/SOFT/MATHCAD/UsersGuide/chapter9/9_7.asp
http://www.math.mrsu.ru/text/courses/mcad/3.5.htm
Пусть
— вектор-столбец,
.
Приведем некоторые известные нормы
векторов:
1.
— эклидова
норма вектора;
2.
— так называемая
—норма,
или норма
Гильберта-Шмидта
(при
совпадает с эвклидовой нормой, а при
совпадает с так называемой 1-нормой).
3.
— чебышевская
норма.
Все эти нормы в
эквивалентны: сходимость в одной из
этих норм влечет за собой сходимость в
другой (следствие конечности
).
Перейдем к понятию матричной
нормы. Пусть
—
множество квадратных вещественных
матриц порядка
.
Пусть каждой матрице
поставлено в соответствие число
.
Это число называется нормой
матрицы A,
если выполняются следующие аксиомы:
1.
;
2.
;
3.
— неравенство
треугольника;
4.
— кольцевое свойство.
Определение 1.
Норма
называется мультипликативной,
если выполняются все четыре аксиомы, и
аддитивной,
если выполняются только первые три
аксиомы.
Определение 2.
Если матричная норма удовлетворяет
условию
|
, |
(1) |
то такая норма
называется согласованной
с нормой вектора.
Большинство
используемых в числовом анализе матричных
норм согласованы с той или иной векторной
нормой.
Определим некоторые
наиболее употребительные на практике
матричные нормы.
—
евклидова
норма или норма Фробениуса
(norm(a,‘fro’)
—
в MATLAB).
—
спектральная
норма
(norm(a)=norm(a,2)
в MATLAB),
где
— собственные значения симметричной
матрицы
(сингулярные числа матрицы А).
Обе указанные нормы согласованы с
эвклидовой нормой вектора
.
—
столбцовая
норма
(norm(a,1)).
(Согласована с векторной нормой
).
—
строчная норма
(norm(a,inf)).
(Согласована с
).
Замечание. Из
всех приведенных матричных норм,
согласованных с евклидовой нормой
вектора, спектральная норма принимает
минимальное значение.
Определение 3.
Число
(вообще говоря, комплексное) называется
собственным
значением матрицы А,
соответствующим собственному вектору
x,
если выполняется условие:
.
(20)
Определение 4.
Множество
всех собственных чисел матрицы А
,
записанных с учетом их кратности,
называется спектром
матрицы А и
обозначается S(A).
Определение 5.
Спектральным
радиусом
r(A)
квадратной матрицы А
называется максимальное по модулю
собственное значение матрицы A.
Система (20) эквивалентна следующей
однородной системе уравнений:
|
|
(21) |
Как известно из
курса линейной алгебры, система (21) имеет
нетривиальные решения тогда и только
тогда, когда
|
|
(22) |
Уравнение (22) —
алгебраическое уравнение n-ой
степени относительно
.
Все его корни – собственные значения
матрицы А.
Определение 6.
Сингулярным
числом
матрицы А
называется собственное значение матрицы
.
Определение 7.
Матрица А
называется положительно (неотрицательно)
определенной (пишут:
или
),
если соответствующая квадратичная
форма
.
Простейшие
следствия из определений.
Следствие 1.
(Критерий
Сильвестра).
все ведущие угловые миноры матрицы А
положительны.
доказывается в курсе линейной алгебры
Следствие 2.
,
причем
.
следует из критерия
Сильвестра.
Следствие 3.
все собственные значения
.
(Для
).
Пусть
— собственное значение, соответствующее
собственному вектору v.
По условию
.
Следствие 4. Пусть
А
– вещественная матрица
матрица
.
Имеем:
{по
св. скалярного произведения}
.
Следствие 5.
Сингулярные
числа вещественной матрицы А
– неотрицательны.
Следует из С.3 и
С.4.
Следствие 6. Пусть
А
– вещественная и симметрическая матрица
.
Имеем:
.
Следствие 7. Если
А
– невырожденная матрица
собственные значения матриц А
и A-1
взаимообратны.
Пусть
результат.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Линейная алгебра для исследователей данных
Время на прочтение
5 мин
Количество просмотров 14K

«Наша [Ирвинга Капланского и Пола Халмоша] общая философия в отношении линейной алгебры такова: мы думаем в безбазисных терминах, пишем в безбазисных терминах, но когда доходит до серьезного дела, мы запираемся в офисе и вовсю считаем с помощью матриц».
Ирвинг Капланский
Для многих начинающих исследователей данных линейная алгебра становится камнем преткновения на пути к достижению мастерства в выбранной ими профессии.
В этой статье я попытался собрать основы линейной алгебры, необходимые в повседневной работе специалистам по машинному обучению и анализу данных.
Произведения векторов
Для двух векторов x, y ∈ ℝⁿ их скалярным или внутренним произведением xᵀy
называется следующее вещественное число:
Как можно видеть, скалярное произведение является особым частным случаем произведения матриц. Также заметим, что всегда справедливо тождество
.
Для двух векторов x ∈ ℝᵐ, y ∈ ℝⁿ (не обязательно одной размерности) также можно определить внешнее произведение xyᵀ ∈ ℝᵐˣⁿ. Это матрица, значения элементов которой определяются следующим образом: (xyᵀ)ᵢⱼ = xᵢyⱼ, то есть
След
Следом квадратной матрицы A ∈ ℝⁿˣⁿ, обозначаемым tr(A) (или просто trA), называют сумму элементов на ее главной диагонали:
След обладает следующими свойствами:
-
Для любой матрицы A ∈ ℝⁿˣⁿ: trA = trAᵀ.
-
Для любых матриц A,B ∈ ℝⁿˣⁿ: tr(A + B) = trA + trB.
-
Для любой матрицы A ∈ ℝⁿˣⁿ и любого числа t ∈ ℝ: tr(tA) = t trA.
-
Для любых матриц A,B, таких, что их произведение AB является квадратной матрицей: trAB = trBA.
-
Для любых матриц A,B,C, таких, что их произведение ABC является квадратной матрицей: trABC = trBCA = trCAB (и так далее — данное свойство справедливо для любого числа матриц).
Нормы
Норму ∥x∥ вектора x можно неформально определить как меру «длины» вектора. Например, часто используется евклидова норма, или норма l₂:
Заметим, что ‖x‖₂²=xᵀx.
Более формальное определение таково: нормой называется любая функция f : ℝn → ℝ, удовлетворяющая четырем условиям:
-
Для всех векторов x ∈ ℝⁿ: f(x) ≥ 0 (неотрицательность).
-
f(x) = 0 тогда и только тогда, когда x = 0 (положительная определенность).
-
Для любых вектора x ∈ ℝⁿ и числа t ∈ ℝ: f(tx) = |t|f(x) (однородность).
-
Для любых векторов x, y ∈ ℝⁿ: f(x + y) ≤ f(x) + f(y) (неравенство треугольника)
Другими примерами норм являются норма l₁
и норма l∞
Все три представленные выше нормы являются примерами норм семейства lp, параметризуемых вещественным числом p ≥ 1 и определяемых как
Нормы также могут быть определены для матриц, например норма Фробениуса:
Линейная независимость и ранг
Множество векторов {x₁, x₂, …, xₙ} ⊂ ℝₘ называют линейно независимым, если никакой из этих векторов не может быть представлен в виде линейной комбинации других векторов этого множества. Если же такое представление какого-либо из векторов множества возможно, эти векторы называют линейно зависимыми. То есть, если выполняется равенство
для некоторых скалярных значений α₁,…, αₙ-₁ ∈ ℝ, то мы говорим, что векторы x₁, …, xₙ линейно зависимы; в противном случае они линейно независимы. Например, векторы
линейно зависимы, так как x₃ = −2xₙ + x₂.
Столбцовым рангом матрицы A ∈ ℝᵐˣⁿ называют число элементов в максимальном подмножестве ее столбцов, являющемся линейно независимым. Упрощая, говорят, что столбцовый ранг — это число линейно независимых столбцов A. Аналогично строчным рангом матрицы является число ее строк, составляющих максимальное линейно независимое множество.
Оказывается (здесь мы не будем это доказывать), что для любой матрицы A ∈ ℝᵐˣⁿ столбцовый ранг равен строчному, поэтому оба этих числа называют просто рангом A и обозначают rank(A) или rk(A); встречаются также обозначения rang(A), rg(A) и просто r(A). Вот некоторые основные свойства ранга:
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) ≤ min(m,n). Если rank(A) = min(m,n), то A называют матрицей полного ранга.
-
Для любой матрицы A ∈ ℝᵐˣⁿ: rank(A) = rank(Aᵀ).
-
Для любых матриц A ∈ ℝᵐˣⁿ, B ∈ ℝn×p: rank(AB) ≤ min(rank(A),rank(B)).
-
Для любых матриц A,B ∈ ℝᵐˣⁿ: rank(A + B) ≤ rank(A) + rank(B).
Ортогональные матрицы
Два вектора x, y ∈ ℝⁿ называются ортогональными, если xᵀy = 0. Вектор x ∈ ℝⁿ называется нормированным, если ||x||₂ = 1. Квадратная м
атрица U ∈ ℝⁿˣⁿ называется ортогональной, если все ее столбцы ортогональны друг другу и нормированы (в этом случае столбцы называют ортонормированными). Заметим, что понятие ортогональности имеет разный смысл для векторов и матриц.
Непосредственно из определений ортогональности и нормированности следует, что
Другими словами, результатом транспонирования ортогональной матрицы является матрица, обратная исходной. Заметим, что если U не является квадратной матрицей (U ∈ ℝᵐˣⁿ, n < m), но ее столбцы являются ортонормированными, то UᵀU = I, но UUᵀ ≠ I. Поэтому, говоря об ортогональных матрицах, мы будем по умолчанию подразумевать квадратные матрицы.
Еще одно удобное свойство ортогональных матриц состоит в том, что умножение вектора на ортогональную матрицу не меняет его евклидову норму, то есть
для любых вектора x ∈ ℝⁿ и ортогональной матрицы U ∈ ℝⁿˣⁿ.
Область значений и нуль-пространство матрицы
Линейной оболочкой множества векторов {x₁, x₂, …, xₙ} является множество всех векторов, которые могут быть представлены в виде линейной комбинации векторов {x₁, …, xₙ}, то есть
Областью значений R(A) (или пространством столбцов) матрицы A ∈ ℝᵐˣⁿ называется линейная оболочка ее столбцов. Другими словами,
Нуль-пространством, или ядром матрицы A ∈ ℝᵐˣⁿ (обозначаемым N(A) или ker A), называют множество всех векторов, которые при умножении на A обращаются в нуль, то есть
Квадратичные формы и положительно полуопределенные матрицы
Для квадратной матрицы A ∈ ℝⁿˣⁿ и вектора x ∈ ℝⁿ квадратичной формой называется скалярное значение xᵀ Ax. Распишем это выражение подробно:
Заметим, что
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно определенной, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx > 0. Обычно это обозначается как
(или просто A > 0), а множество всех положительно определенных матриц часто обозначают
.
-
Симметричная матрица A ∈ 𝕊ⁿ называется положительно полуопределенной, если для всех векторов справедливо неравенство xᵀ Ax ≥ 0. Это записывается как
(или просто A ≥ 0), а множество всех положительно полуопределенных матриц часто обозначают
.
-
Аналогично симметричная матрица A ∈ 𝕊ⁿ называется отрицательно определенной
-
, если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx < 0.
-
Далее, симметричная матрица A ∈ 𝕊ⁿ называется отрицательно полуопределенной (
), если для всех ненулевых векторов x ∈ ℝⁿ справедливо неравенство xᵀAx ≤ 0.
-
Наконец, симметричная матрица A ∈ 𝕊ⁿ называется неопределенной, если она не является ни положительно полуопределенной, ни отрицательно полуопределенной, то есть если существуют векторы x₁, x₂ ∈ ℝⁿ такие, что
и
.
Собственные значения и собственные векторы
Для квадратной матрицы A ∈ ℝⁿˣⁿ комплексное значение λ ∈ ℂ и вектор x ∈ ℂⁿ будут соответственно являться собственным значением и собственным вектором, если выполняется равенство
На интуитивном уровне это определение означает, что при умножении на матрицу A вектор x сохраняет направление, но масштабируется с коэффициентом λ. Заметим, что для любого собственного вектора x ∈ ℂⁿ и скалярного значения с ∈ ℂ справедливо равенство A(cx) = cAx = cλx = λ(cx). Таким образом, cx тоже является собственным вектором. Поэтому, говоря о собственном векторе, соответствующем собственному значению λ, мы обычно имеем в виду нормализованный вектор с длиной 1 (при таком определении все равно сохраняется некоторая неоднозначность, так как собственными векторами будут как x, так и –x, но тут уж ничего не поделаешь).
Перевод статьи был подготовлен в преддверии старта курса «Математика для Data Science». Также приглашаем всех желающих посетить бесплатный демоурок, в рамках которого рассмотрим понятие линейного пространства на примерах, поговорим о линейных отображениях, их роли в анализе данных и порешаем задачи.
-
ЗАПИСАТЬСЯ НА ДЕМОУРОК
-
-
May 28 2018, 08:04
- Наука
- Cancel
Норма Фробениуса
Норма Фробениуса или, как её ещё называют Евклидова норма, — это квадратный корень сумм квадратов модулей элементов матрицы размера m × n:
Простой пример. Есть матрица размера 3 × 3:
Она же, но с элементами, возведёнными в квадрат:
Сумма элементов этой матрицы будет равна 60. Квадратный корень из 60 примерно равен 7,746. Это число и есть норма Фробениуса для нашей матрицы.
Есть иной способ вычисления нормы Фробениуса: как квадратный корень произведения следа этой матрицы и эрмитово-сопряжённой матрицы:
https://ru.wikipedia.org/wiki/Норма_матрицы#Норма_Фробениуса
In mathematics, a matrix norm is a vector norm in a vector space whose elements (vectors) are matrices (of given dimensions).
Preliminaries[edit]
Given a field 





This article will always write such norms with double vertical bars (like so: 

For all scalars 

The only feature distinguishing matrices from rearranged vectors is multiplication. Matrix norms are particularly useful if they are also sub-multiplicative:[1][2][3]
[Note 1]
Every norm on Kn×n can be rescaled to be sub-multiplicative; in some books, the terminology matrix norm is reserved for sub-multiplicative norms.[4]
Matrix norms induced by vector norms[edit]
Suppose a vector norm 








where 

Depending on the vector norms 


Matrix norms induced by vector p-norms[edit]
If the p-norm for vectors (


These induced norms are different from the «entry-wise» p-norms and the Schatten p-norms for matrices treated below, which are also usually denoted by 
In the special cases of 
which is simply the maximum absolute column sum of the matrix;
which is simply the maximum absolute row sum of the matrix.
For example, for
we have that
In the special case of 






where 

since 

where 

When 


Matrix norms induced by vector α- and β- norms[edit]
Suppose vector norms 



In the special cases of 

where 

In the special cases of 

where 

Hence, 

Properties[edit]
Any operator norm is consistent with the vector norms that induce it, giving
Suppose 





this follows from
and
Square matrices[edit]
Suppose 
induced by vector norms 

Then, the operator norm is a sub-multiplicative matrix norm:
Moreover, any such norm satisfies the inequality
|
|
(1) |
for all positive integers r, where ρ(A) is the spectral radius of A. For symmetric or hermitian A, we have equality in (1) for the 2-norm, since in this case the 2-norm is precisely the spectral radius of A. For an arbitrary matrix, we may not have equality for any norm; a counterexample would be
which has vanishing spectral radius. In any case, for any matrix norm, we have the spectral radius formula:
Consistent and compatible norms[edit]
A matrix norm 





for all 




All induced norms are consistent by definition. Also, any sub-multiplicative matrix norm on 


«Entry-wise» matrix norms[edit]
These norms treat an 

This is a different norm from the induced p-norm (see above) and the Schatten p-norm (see below), but the notation is the same.
The special case p = 2 is the Frobenius norm, and p = ∞ yields the maximum norm.
L2,1 and Lp,q norms[edit]
Let 



The 
For p, q ≥ 1, the 

Frobenius norm[edit]
When p = q = 2 for the 
where 

The Frobenius norm is an extension of the Euclidean norm to 
The Frobenius norm is sub-multiplicative and is very useful for numerical linear algebra. The sub-multiplicativity of Frobenius norm can be proved using Cauchy–Schwarz inequality.
Frobenius norm is often easier to compute than induced norms, and has the useful property of being invariant under rotations (and unitary operations in general). That is, 


and analogously:
where we have used the unitary nature of 

It also satisfies
and
where 
Max norm[edit]
The max norm is the elementwise norm in the limit as p = q goes to infinity:
This norm is not sub-multiplicative.
Note that in some literature (such as Communication complexity), an alternative definition of max-norm, also called the 
Schatten norms[edit]
The Schatten p-norms arise when applying the p-norm to the vector of singular values of a matrix.[2] If the singular values of the 

These norms again share the notation with the induced and entry-wise p-norms, but they are different.
All Schatten norms are sub-multiplicative. They are also unitarily invariant, which means that 



The most familiar cases are p = 1, 2, ∞. The case p = 2 yields the Frobenius norm, introduced before. The case p = ∞ yields the spectral norm, which is the operator norm induced by the vector 2-norm (see above). Finally, p = 1 yields the nuclear norm (also known as the trace norm, or the Ky Fan ‘n’-norm[7]), defined as:

where 





Combining von Neumann’s trace inequality
with Hölder’s inequality for Euclidean space
yields a version of Hölder’s inequality
for Schatten norms
for


In particular, this implies the Schatten norm inequality

Monotone norms[edit]
A matrix norm 
The Frobenius norm and spectral norm are examples of monotone norms.[8]
Cut norms[edit]
Another source of inspiration for matrix norms arises from considering a matrix as the adjacency matrix of a weighted, directed graph.[9] The so-called «cut norm» measures how close the associated graph is to being bipartite:
where A ∈ Km×n.[9][10][11] Equivalent definitions (up to a constant factor) impose the conditions 2|S| > n & 2|T| > m; S = T; or S ∩ T = ∅.[10]
The cut-norm is equivalent to the induced operator norm ‖·‖∞→1, which is itself equivalent to the another norm, called the Grothendieck norm.[11]
To define the Grothendieck norm, first note that a linear operator K1 → K1 is just a scalar, and thus extends to a linear operator on any Kk → Kk. Moreover, given any choice of basis for Kn and Km, any linear operator Kn → Km extends to a linear operator (Kk)n → (Kk)m, by letting each matrix element on elements of Kk via scalar multiplication. The Grothendieck norm is the norm of that extended operator; in symbols:[11]
The Grothendieck norm depends on choice of basis (usually taken to be the standard basis) and k.
Equivalence of norms[edit]
For any two matrix norms 

for some positive numbers r and s, for all matrices 




Moreover, for every vector norm 




A sub-multiplicative matrix norm 


Examples of norm equivalence[edit]
Let 
For matrix 

See also[edit]
- Dual norm
- Logarithmic norm
Notes[edit]
- ^ The condition only applies when the product is defined, such as the case of square matrices (m = n).
References[edit]
- ^ a b Weisstein, Eric W. «Matrix Norm». mathworld.wolfram.com. Retrieved 2020-08-24.
- ^ a b c d «Matrix norms». fourier.eng.hmc.edu. Retrieved 2020-08-24.
- ^ Malek-Shahmirzadi, Massoud (1983). «A characterization of certain classes of matrix norms». Linear and Multilinear Algebra. 13 (2): 97–99. doi:10.1080/03081088308817508. ISSN 0308-1087.
- ^ Horn, Roger A. (2012). Matrix analysis. Johnson, Charles R. (2nd ed.). Cambridge: Cambridge University Press. pp. 340–341. ISBN 978-1-139-77600-4. OCLC 817236655.
- ^ Carl D. Meyer, Matrix Analysis and Applied Linear Algebra, §5.2, p.281, Society for Industrial & Applied Mathematics, June 2000.
- ^ Ding, Chris; Zhou, Ding; He, Xiaofeng; Zha, Hongyuan (June 2006). «R1-PCA: Rotational Invariant L1-norm Principal Component Analysis for Robust Subspace Factorization». Proceedings of the 23rd International Conference on Machine Learning. ICML ’06. Pittsburgh, Pennsylvania, USA: ACM. pp. 281–288. doi:10.1145/1143844.1143880. ISBN 1-59593-383-2.
- ^ Fan, Ky. (1951). «Maximum properties and inequalities for the eigenvalues of completely continuous operators». Proceedings of the National Academy of Sciences of the United States of America. 37 (11): 760–766. Bibcode:1951PNAS…37..760F. doi:10.1073/pnas.37.11.760. PMC 1063464. PMID 16578416.
- ^ Ciarlet, Philippe G. (1989). Introduction to numerical linear algebra and optimisation. Cambridge, England: Cambridge University Press. p. 57. ISBN 0521327881.
- ^ a b Frieze, Alan; Kannan, Ravi (1999-02-01). «Quick Approximation to Matrices and Applications». Combinatorica. 19 (2): 175–220. doi:10.1007/s004930050052. ISSN 1439-6912. S2CID 15231198.
- ^ a b Lovász László (2012). «The cut distance». Large Networks and Graph Limits. AMS Colloquium Publications. Vol. 60. Providence, RI: American Mathematical Society. pp. 127–131. ISBN 978-0-8218-9085-1. Note that Lovász rescales ‖A‖□ to lie in [0, 1].
- ^ a b c Alon, Noga; Naor, Assaf (2004-06-13). «Approximating the cut-norm via Grothendieck’s inequality». Proceedings of the Thirty-Sixth Annual ACM Symposium on Theory of Computing. STOC ’04. Chicago, IL, USA: Association for Computing Machinery: 72–80. doi:10.1145/1007352.1007371. ISBN 978-1-58113-852-8. S2CID 1667427.
- ^
Golub, Gene; Charles F. Van Loan (1996). Matrix Computations – Third Edition. Baltimore: The Johns Hopkins University Press, 56–57. ISBN 0-8018-5413-X. - ^ Roger Horn and Charles Johnson. Matrix Analysis, Chapter 5, Cambridge University Press, 1985. ISBN 0-521-38632-2.
Bibliography[edit]
- James W. Demmel, Applied Numerical Linear Algebra, section 1.7, published by SIAM, 1997.
- Carl D. Meyer, Matrix Analysis and Applied Linear Algebra, published by SIAM, 2000. [1]
- John Watrous, Theory of Quantum Information, 2.3 Norms of operators, lecture notes, University of Waterloo, 2011.
- Kendall Atkinson, An Introduction to Numerical Analysis, published by John Wiley & Sons, Inc 1989

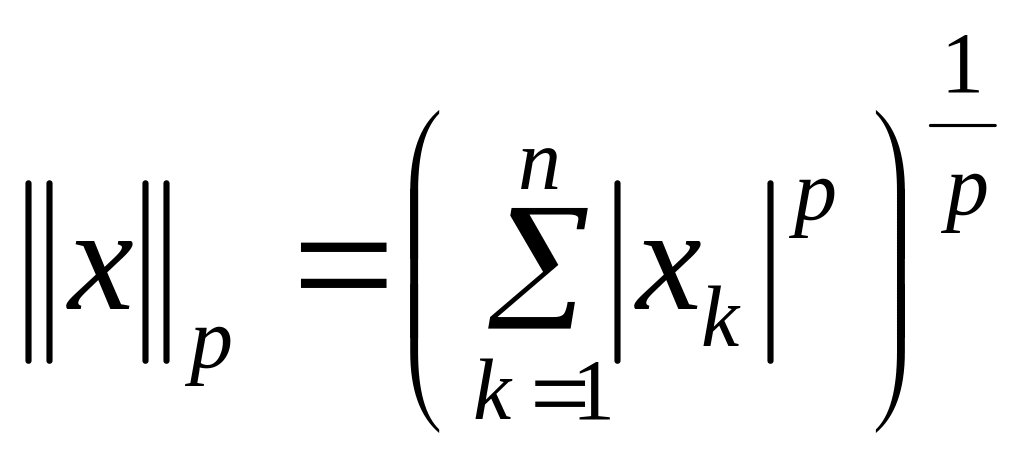
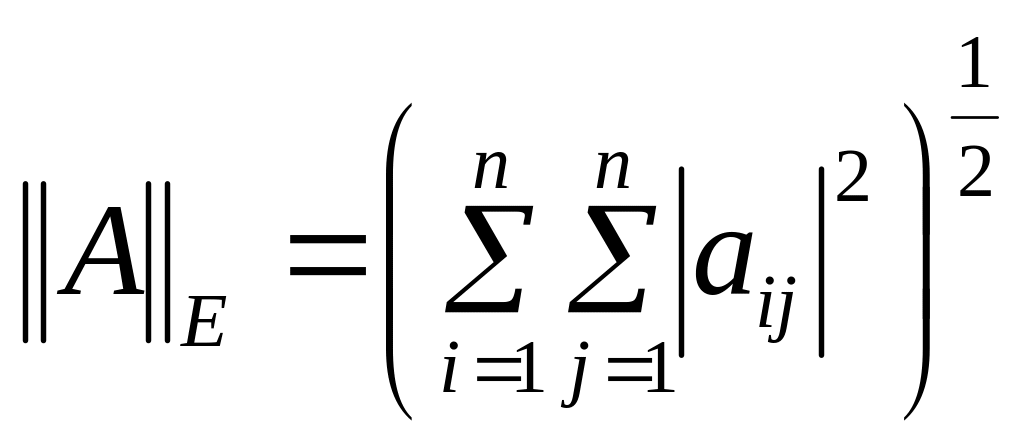






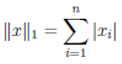











































![{displaystyle |A|_{Box }=max _{Ssubseteq [n],Tsubseteq [m]}{left|sum _{sin S,tin T}{A_{t,s}}right|}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/81f549cf8e017790e477cbd11624fb7a8d5f239a)
![{displaystyle |A|_{G,k}=sup _{{text{each }}u_{j},v_{j}in K^{k};|u_{j}|=|v_{j}|=1}{sum _{jin [n],lin [m]}{(u_{j}cdot v_{j})A_{l,j}}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2fb3bc95adcb08feaf7e57fe7f21cf15abb42a74)
