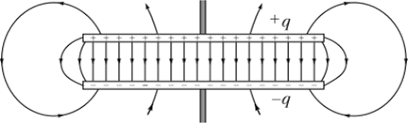
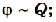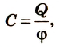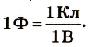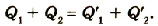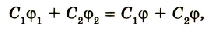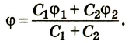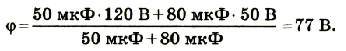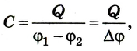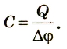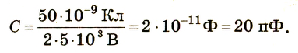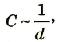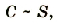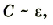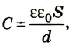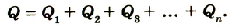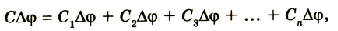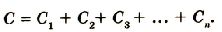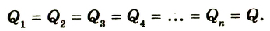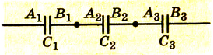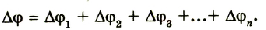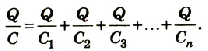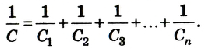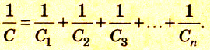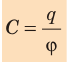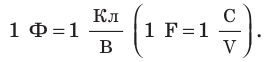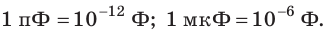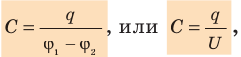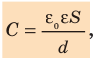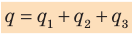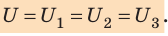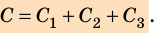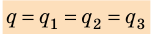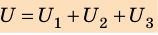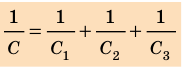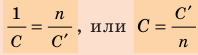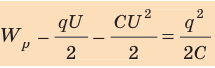Содержание:
Электроемкость:
Сообщая телу определенный заряд, мы изменяем его потенциал. Это изменение непосредственно связано со значением заряда, сообщаемого телу.
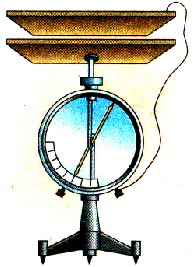
Для исследования зависимости потенциала тела от его заряда проведем опыт с электрометром, корпус которого соединен с поверхностью Земли. ‘Гикая система может измерять потенциал тела относительно Земли. Укрепим на стержне этого электрометра пустотелый металлический шар и будем сообщать ему заряд с помощью маленького металлического шарика на изоляционной ручке. Если коснуться заряженным шариком внутренней поверхности металлического шара, то весь его заряд перейдет на шар, а стрелка электрометра покажет увеличение потенциала шара. Последовательно повторяя опыт с переносом заряда на большой шар, заметим, что каждый раз его потенциал увеличивается (рис. 1.28).
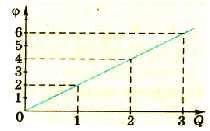
Применяя более точные способы измерения заряда и потенциала, можно установить, что потенциал возрастает пропорционально возрастанию заряда. Потенциал пропорционален заряду шара. Результаты одного из таких опытов отражены на графике (рис 1.29).
Если ни стержне электрометра укрепим шар большего (меньшего) диаметра и продолжим опыты (рис. 1.31), то увидим, что скорость зарядки изменилась, соответственно уменьшилась (увеличилась).
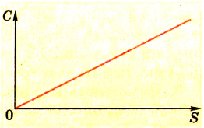
Процесс электризации шара большего диаметра отображен графиком на рисунке 1.32.
Сопоставив графики, которые иллюстрируют процессы зарядки шаров различных диаметров (рис. 1.30 и 1.32), увидим, что графики имеют различный наклон относительно горизонтальной оси. Это свидетельствует о том, что при одинаковых значениях заряда шары разных диаметров будут иметь разные потенциалы. Оказывается, что на князь между зарядом и потенциалом шара существенно влияют геометрические размеры шаров.
Рис. 130. Электризация шара большего диаметра
Потенциал металлического шара пропорционален его заряду; коэффициент пропорциональности для различных шаров разный.
Анализируя результаты опытов и соответствующие графики, можно сделать выводы:
- потенциал каждого шара пропорционален его заряду:
- для тел различных размеров коэффициент пропорциональности разный.
Установлено, что этот коэффициент для каждого тела имеет вполне определенное значение, что отражает способность тела накапливать электрический заряд. Физическая величина, равная отношению электрического заряда, сообщенного телу, к его потенциалу, называется электроемкостью тела.
где C — электроемкость проводника; Q — заряд; φ — потенциал.
Для измерения электроемкости в физике применяют единицу, которую называют фарад (Ф).
Тело имеет электроемкость в 1 фарад, если при изменении его заряда на 1 кулон потенциал изменяется па 1 вольт:
Электроемкость 1 фарад имеют тела, у которых при изменении заряда на 1 кулон потенциал изменяется на 1 вольт.
- 1Ф — довольно большое значение электроемкости. Например, электроемкость Земли, имеющей радиус 6400 км, составляет всего 7 ∙ 104 Ф. Поэтому на практике используют единицу электроемкости, кратную фараду:
- 1 микрофарад = 1 мкФ = 10-5 Ф.
- 1 пикофарад = 1 пФ = 10-12 Ф.
Пример:
Два шара, электроемкости которых 50 мкф и 80 мкФ, а потенциалы 120 В и 50 В соответственно, соединяют проводом. Найти потенциал шаров после соединения.
|
Дано: |
Решение |
| φ-? |
После соединения шаров произойдет перераспределение зарядов между ними так, что их потенциалы станут одинаковыми. Согласно закону сохранения электрических зарядов
Отсюда
или
Подставив значения физических величин и произведя расчеты, получим:
Ответ: после соединения шары будут иметь потенциал 77 В.
Конденсатор
Чтобы экспериментально определить электроемкость проводника, как и его потенциал, нужно создать условия, исключающие влияние всех окружающих тел, которые, влияя па тело, изменяют его потенциал и электроемкость.
Это утверждение можно проверить опытом.
Укрепим на стержне электрометра металлический шар и сообщим ему определенный заряд. Стрелка прибора отклонится от положения равновесия и покажет определенное значение потенциала относительно земли.
Поднесем к шару металлическую пластину, соединенную проводником с землей (рис. 1.32).
Pиc. 132. Заземленная металлическая пластина влияет на электроемкость шара
Показания стрелки электрометра уменьшатся. Поскольку заряд шара в опыте не изменялся, то уменьшение потенциала свидетельствует об увеличении электроемкости шара. Изменение потенциала и соответственно электроемкости шара будет наблюдаться и в случае изменения расстояния между шаром и пластиной.
Таким образом, определяя электроемкость тела, необходимо учитывать также наличие окружающих тел. Поскольку на практике это сделать трудно, то применяют систему из двух или более проводников произвольной формы, разделенных диэлектриком. В этом случае электрические свойства такой системы проводников и диэлектрика не зависят от окружающих тел. Такую систему называют конденсатором. Простейшим для изучения и расчетов является конденсатор из двух металлических пластин, разделенных диэлектриком.
Электроемкость конденсатора, в отличие от обособленного тела, определяется по разности потенциалов между пластинами:
где Q — заряд одной пластины; (φl— φ2) и ∆φ — разность потенциалов между пластинами.
Слово конденсатор обозначает накопитель. В электричестве понимают как «накопитель электрических зарядов».
Пример:
Какую электроемкость имеет конденсатор, если на его обкладках накапливается заряд 50 нКл при разности потенциалов 2,5 кВ?
|
Дано: |
Решение |
| С-? |
Подставим значения физических величин:
Ответ: электроемкость данного конденсатора 20 пФ.
Первый конденсатор был создан в 1745 г. голландским ученым Питером ван Мушенбруком, профессором Лейденского университета. Проводя опыты по электризации различных тел, он опустил проводник от кондуктора электрической машины в стеклянный графин с водой (рис. 1.33).
 |
Питер ван Мушенбрук (1692-1781) — голландский физик; работы посвящены электричеству, теплоте, оптике; изобрел первый конденсатор — лейденскую банку и провел опыты с ней. |
Pиc. 133. Из истории открытия простейшего конденсатора лейденской банки
Случайно коснувшись пальцем этого проводника, ученый ощутил сильный электрический удар. В дальнейшем жидкость заменили металлическими проводниками, укрепленными на внутренней и внешней поверхностях банки. Такой конденсатор назвали лейденской банкой. В таком первозданном виде она использовалась в лабораториях более 200 лет.
Более совершенные конденсаторы применяются в современной электротехнике и радиоэлектронике. Их можно найти в преобразователях напряжения (адаптерах), питающих постоянным электрическим током электронные приборы, в радиоприемниках и радиопередатчиках как поставные части колебательных контуров. Они применяются практически во всех функциональных узлах электронной аппаратуры. В фотовспышках конденсаторы накапливают большие заряды, необходимые для действия вспышки.
В электротехнике конденсаторы обеспечивают необходимый режим работы электродвигателей, автоматических и релейных приборов, линий электропередач и т. п.
Во многих широкодиапазонных радиоприемниках конденсаторы переменной емкости (рис. 1.34) позволяют плавно изменять собственную частоту колебательного контура н процессе поиска передачи определенной радиостанции.
Рис. 134. Конденсатор переменной емкости с воздушным диэлектриком
Весьма распространены конденсаторы варикапы, электроемкость которых можно изменять электрическим способом. Конструктивно они весьма схожи с полупроводниковыми диодами.
Конденсаторы могут быть плоскими, трубчатыми, дисковыми. В качестве диэлектрика в них используют парафинированную бумагу, слюду, воздух, пластмассы, керамику (рис. 1.35).
Рис. 1.35. Различные типы конденсаторов
Искусственно созданные диэлектрические материалы позволяют создавать конденсаторы больших емкостей при небольших размерах.
Электроемкость плоского конденсатора
Плоским конденсатором обычно называют систему плоских проводящих пластин — обкладок, разделенных диэлектриком. Благодаря простоте конструкции такого конденсатора легко рассчитывать его емкость и получать значения, подтверждаемые опытами. Для этого достаточно знать его геометрические параметры и электрические свойства диэлектрика между его пластинами. Зависимость электроемкости плоского конденсатора от указанных параметров можно исследовать в школьной лаборатории.
Создадим плоский конденсатор из двух плоских пластин. Для этого одну пластину укрепим на стержне электрометра, я другую — па изоляционной подставке, присоединив ее проводником к корпусу электрометра (рис. 1.36.). В такой системе электрометр будет измерять разность потенциалов между пластинами, образующими плоский конденсатор.
Pиc. 136. Плоский конденсатор, присоединенный к электрометру
Проводя исследования, нужно помнить, что при постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
При постоянном значении заряда на пластинах уменьшение разности потенциалов свидетельствует об увеличении электроемкости конденсатора, и наоборот.
Сообщим пластинам некоторый заряд и отметим показания стрелки прибора. Когда начнем сближать пластины, уменьшая расстояние между ними, показания стрелки начнут уменьшаться. Это будет свидетельством того, что при уменьшении расстояния между пластинами электроемкость конденсатора будет увеличиваться. При увеличении расстояния между пластинами показания стрелки будут увеличиваться, что свидетельствует об уменьшении электроемкости.
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
где d — расстояние между обкладками.
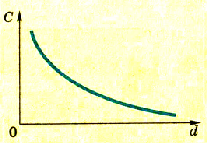
Эту, зависимость можно изобразить на графике как обратно пропорциональную зависимость (рис. 1.37).
Электроемкость плоского конденсатора обратно пропорциональна расстоянию между его обкладками.
Pиc. 137. График зависимости электроемкости и плоского конденсатора от расстояния между пластинами
Будем смещать одну пластину относительно другой в параллельных плоскостях, не изменяя расстояния между ними. При атом площадь перекрытия между пластинами будет изменяться (рис. 1.38). Изменение разности потенциалов, отмеченное электрометром, засвидетельствует изменение электроемкости.
Pиc. 138. При расчетах электроемкости плоского конденсатора учитывают площадь перекрытия пластин
Увеличение площади перекрытия приведет к увеличению электроемкости, при уменьшении — наоборот.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
где S — площадь пластин, которые перекрываются.
Электроемкость плоского конденсатора пропорциональна площади пластин, которые перекрываются.
Эту зависимость можно изобразить графиком прямой пропорциональной зависимости (рис. 1.39).
Pиc. 139. График зависимости электроемкости плоского конденсатора от площади его пластин
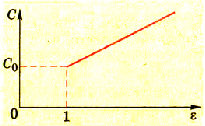
Возвратив пластины в первоначальное положение, внесем в пространство между обкладками пластину из диэлектрика. Электрометр отметит уменьшение разности потенциалов между пластинами, что свидетельствует об увеличении электроемкости. Если внести пластину из другого диэлектрика (другая диэлектрическая проницаемость), то изменение электроемкости будет другим.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика между обкладками.
где ε — диэлектрическая проницаемость диэлектрика.
Эта зависимость изображена графиком на рисунке 1.40.
Рис. 1.40. График зависимости электроемкости плоского конденсатора от диэлектрической проницаемости диэлектрика
Результаты описанных выше исследований можно обобщить формулой электроемкости плоского конденсатора
где ε — относительная диэлектрическая проницаемость диэлектрика; ε0— электрическая постоянная; d — расстояние между пластинами; S — площадь пластины.
Электроемкость плоского конденсатора зависит от диэлектрической проницаемости диэлектрика.
Соединение конденсаторов в батареи
Для получения необходимых значений электроемкости конденсаторы соединяют в батареи. На практике встречается параллельное, последовательное и смешанное соединение конденсаторов.
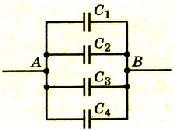
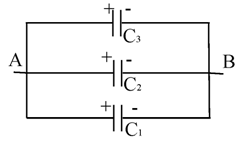
При параллельном соединении конденсаторов все обкладки соединяются в две группы, в каждую из которых входит по одной обкладке каждого конденсатора. На рисунке 1.41 приведена схема такого соединения. При таком соединении каждая группа обкладок имеет одинаковый потенциал.
Pиc 1.41. Схема параллельного соединения конденсаторов
Если батарею параллельно соединенных конденсаторов зарядить, то между обкладками каждого конденсатора будет одинаковая разность потенциалов. Общий заряд батареи будет равен сумме зарядов каждого из конденсаторов, входящих в батарею:
Если учесть, что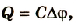 
то
или
Электроемкость батареи параллельно соединенных конденсаторов равна сумме электроемкостей всех конденсаторов.
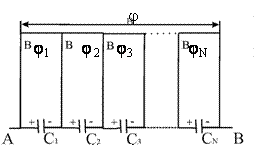
При последовательном соединении конденсаторов соединяются между собой только две пластины разных конденсаторов. Если в каждом конденсаторе пластины обозначить буквами А и В, то при последовательном соединении пластина B1 будет соединена с пластиной A2, пластина B2 -с пластиной А3 и т. д. (рис. 1.43).
Если цепочку последовательно соединенных конденсаторов присоединить к источнику тока, то об-
кладка A1 и обкладка B1 будут иметь одинаковые по значению заряды +Q и -Q. Благодаря этому все обкладки внутри цепочки будут иметь такие же, но попарно противоположные по знаку заряды:
Pиc. 1.42. Последовательное соединение конденсаторов
Вместе с тем общая разность потенциалов на концах цепочки будет равна сумме разностей потенциалов на каждом конденсаторе:
Учитывая, что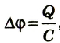 
будем иметь
Разделим левую и правую части равенства на Q:
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно с
При последовательном соединении конденсаторов обратное значение электроемкости цепочки равно сумме обратных значений электроемкостей каждого из конденсаторов.
При последовательном соединении конденсаторов разной электроемкости C1, C2, C3, … Сn общая электроемкость С будет меньше электроемкости самого меньшего конденсатора.
Если C1 < C7 < C9 < … < Cn, то C < C1.
Электроемкость
То, что деньги хранят в банках, знает даже первоклассник. А вот где хранят заряды? И зачем вообще хранить заряды?
Что такое электроемкость
Электроемкость характеризует способность проводника или системы проводников накапливать электрический заряд. Различают электроемкость уединенного проводника и электроемкость системы проводников (например, конденсатора). Уединенным называют проводник, расположенный вдали от других тел так, что они не оказывают на этот проводник никакого влияния.
Электроемкость уединенного проводника (C) — физическая величина, характеризующая способность проводника накапливать заряд и равная отношению электрического заряда q проводника к его потенциалу М:
Единица электроемкости в Си — фарад: [C] = 1 Ф (названа в честь М. Фарадея).
1 Ф — это электроемкость такого проводника, потенциал которого равен 1 В при сообщении ему заряда 1 Кл; 
1 Ф — очень большая единица емкости, поэтому используют дольные единицы: 
Что такое конденсатор
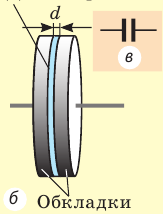
Конденсатор — устройство, представляющее собой систему из двух проводящих обкладок, разделенных тонким слоем диэлектрика (рис. 44.1).
Рис. 44.1. Школьный воздушный конденсатор: а — вид; б — устройство; в — обозначение на схемах
Обкладкам конденсатора передают одинаковые по модулю, но противоположные по знаку заряды, что способствует накоплению зарядов: разноименные заряды притягиваются, а значит, располагаются на внутренних поверхностях обкладок.
Обычно для зарядки конденсатора обе его обкладки соединяют с полюсами батареи аккумуляторов: на обкладках появляются равные по модулю, но противоположные по знаку заряды. Результат не изменится, если соединить с полюсом батареи только одну обкладку, заземлив вторую: вследствие электростатической индукции на заземленной обкладке тоже появится заряд, равный по модулю заряду на другой обкладке, но имеющий противоположный знак.
Зарядом конденсатора называют модуль заряда одной из обкладок. Отношение заряда q данного конденсатора к разности потенциалов (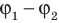
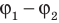
) между его обкладками не зависит ни от значения q, ни от разности потенциалов (
), а значит, может служить характеристикой конденсатора. Такую характеристику называют электроемкостью (емкостью) конденсатора:
где U — напряжение между обкладками: .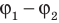
Как показывают исследования, емкость конденсатора увеличится, если увеличить площадь поверхности обкладок или приблизить обкладки друг к другу. На емкость конденсатора влияет также диэлектрик: чем больше его диэлектрическая проницаемость, тем большую емкость имеет конденсатор.
Конденсатор, состоящий из двух параллельных металлических пластин (обкладок), разделенных слоем диэлектрика, называют плоским (см. рис. 44.1). Электроемкость плоского конденсатора вычисляют по формуле:
где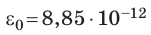 
Ф/м — электрическая постоянная; ε — диэлектрическая проницаемость диэлектрика; S — площадь пластины конденсатора; d — расстояние между пластинами.
Поле между пластинами плоского конденсатора однородно, поэтому напряженность Е поля связана с напряжением U на конденсаторе формулой U=Ed.
Как рассчитывают электроемкость батареи конденсаторов
Конденсаторы характеризуются емкостью и максимальным рабочим напряжением Umax. Если напряжение, поданное на конденсатор, значительно превысит Umax, произойдет пробой — между обкладками возникнет искра, которая разрушит изоляцию.
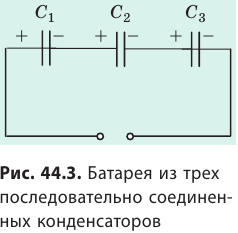
Чтобы получить необходимую электроемкость при определенном рабочем напряжении, конденсаторы соединяют в батареи, применяя параллельное, последовательное и смешанное соединения. Рассмотрим батарею из трех конденсаторов электроемкостями 
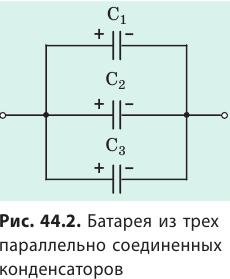
При параллельном соединении конденсаторов положительно заряженные обкладки всех конденсаторов соединяют в один узел, а отрицательно заряженные — в другой узел (рис. 44.2). В таком случае общий заряд q батареи конденсаторов равен алгебраической сумме зарядов отдельных конденсаторов:
Соединенные в один узел обкладки представляют собой один проводник, поэтому потенциалы обкладок, а следовательно, и разность потенциалов (напряжение) между обкладками всех конденсаторов одинаковы:
Таким образом, при параллельном соединении конденсаторов допустимое рабочее напряжение батареи определяется рабочим напряжением одного конденсатора.
Поскольку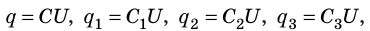 
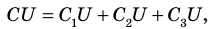
то 
следовательно, электроемкость батареи из трех параллельно соединенных конденсаторов равна:
При последовательном соединении конденсаторы соединяют друг с другом разноименно заряженными обкладками (рис. 44.3). В этом случае заряды всех конденсаторов будут одинаковы и равны заряду батареи:
Напряжение на батарее последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах:
Таким образом, допустимое рабочее напряжение батареи последовательно соединенных конденсаторов больше допустимого рабочего напряжения отдельного конденсатора. Электроемкость батареи последовательно соединенных конденсаторов вычисляют по формуле:
При последовательном соединении конденсаторов емкость батареи меньше, чем емкость конденсатора с минимальной емкостью.
Приведенные соотношения можно обобщить для любого количества конденсаторов.
Обратите внимание!
- Если батарея содержит n параллельно соединенных конденсаторов электроемкостью C′ каждый, то: C=nC′
- Если батарея содержит n последовательно соединенных конденсаторов электроемкостью C′ каждый, то:
Энергия заряженного конденсатора
Заряженный конденсатор, как и любая другая система заряженных тел, обладает энергией.
Убедимся в этом с помощью простого эксперимента. Присоединим к обкладкам заряженного конденсатора лампочку. Замкнем ключ — лампочка загорится. Теперь измерим напряжение на обкладках конденсатора — оно равно нулю, то есть конденсатор разрядился, а это означает, что заряженный конденсатор обладал энергией, которая частично превратилась в энергию света.
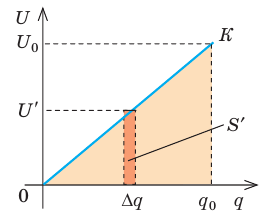
Вычислим энергию заряженного до напряжения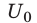 
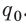
конденсатора емкостью С, на котором накоплен заряд 
. Эту энергию точнее было бы назвать энергией электростатического поля, которое существует между обкладками заряженного конденсатора, поскольку энергия любых заряженных тел сосредоточена в электрическом поле, создаваемом этими телами.
При разрядке конденсатора напряжение U на его обкладках изменяется прямо пропорционально заряду q конденсатора: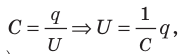 
поэтому график зависимости U(q) имеет вид, представленный на рис. 44.4.
Рис. 44.4. К определению работы, которую совершает электрическое поле заряженного конденсатора при его разрядке
Мысленно разделим весь заряд конденсатора на маленькие «порции» Dq и будем считать, что при потере каждой такой «порции» напряжение на конденсаторе не изменяется. Таким образом получим ряд полос. Площадь S′ каждой полосы равна произведению двух ее сторон: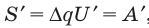 
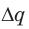
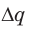
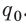
, где U′ — напряжение, при котором конденсатор терял данную «порцию» заряда 
; A′ — работа, которую совершило поле при потере конденсатором заряда 
. Полная работа, которую совершило поле при уменьшении заряда конденсатора от до 0, определяется площадью выделенного на рис. 44.4 треугольника.
Следовательно,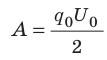
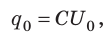
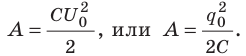
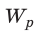
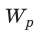
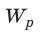
. Учитывая, что
получим: 
С другой стороны, данная работа равна уменьшению энергии электрического поля конденсатора от 
до нуля: A=
− 0 = W. Таким образом, энергия 
заряженного до напряжения U конденсатора, имеющего электроемкость С и заряд q, равна:
Для чего нужны конденсаторы
В современной технике сложно найти отрасль, где не применялись бы конденсаторы. Без них не обходятся радио и телеаппаратура (настройка колебательных контуров), радиолокационная и лазерная техника (получение мощных импульсов), телефония и телеграфия (разделение цепей переменного и постоянного токов, тушение искр в контактах), электроизмерительная техника (создание образцов емкости). И это далеко не полный перечень.
В современной электроэнергетике конденсаторы тоже имеют широкое применение: они присутствуют в конструкциях люминесцентных светильников, электросварочных аппаратов, устройств защиты от перенапряжений. Конденсаторы применяют и в других, не электротехнических, областях техники и промышленности (в медицине, фототехнике и т. д.).
Разнообразие областей применения обусловливает большое разнообразие конденсаторов. Наряду с миниатюрными конденсаторами, имеющими массу меньше грамма, а размеры порядка нескольких миллиметров, существуют конденсаторы массой несколько тонн и высотой больше человеческого роста. Емкость современных конденсаторов может составлять от долей, а рабочее напряжение может быть в пределах от нескольких вольт до нескольких сотен киловольт. Конденсаторы можно классифицировать по следующим признакам и свойствам:
- по назначению — постоянной и переменной емкости;
- по форме обкладок — плоские, сферические, цилиндрические и др.;
- по типу диэлектрика — воздушные, бумажные, слюдяные, керамические, электролитические и др.
Выводы:
- Энергию заряженного конденсатора можно вычислить по формулам:
- Конденсаторы классифицируют по назначению (постоянной и переменной емкости); по форме обкладок (плоские, сферические, цилиндрические и др.); по типу диэлектрика (воздушные, бумажные, слюдяные, керамические, электролитические и др.).
- Полупроводники
- Потенциал электрического поля
- Постоянный электрический ток
- Законы постоянного тока
- Принцип суперпозиции электрических полей
- Проводники в электрическом поле
- Диэлектрики в электрическом поле
- Закон Кулона
Проводники и диэлектрики в электростатическом поле. Диэлектрическая проницаемость вещества. Электроемкость. Конденсаторы. Поле плоского конденсатора. Электроемкость плоского конденсатора. Последовательное и параллельное соединение конденсаторов. Энергия заряженного конденсатора.
Проводники и диэлектрики в электростатическом поле
Вещества в природе можно разделить на проводники и диэлектрики.
Основная особенность — наличие свободных зарядов (электронов), которые участвуют в тепловом движении и могут перемещаться по всему объему проводника.
Типичные проводники — металлы.
Диэлектрическая проницаемость вещества
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды. Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды — индукционными зарядами.
В отличие от проводников, в диэлектриках (изоляторах) нет свободных электрических зарядов. Они состоят из нейтральных атомов или молекул. Заряженные частицы в нейтральном атоме связаны друг с другом и не могут перемещаться под действием электрического поля по всему объему диэлектрика.
Физическая величина, равная отношению модуля напряженности (vec{E}_0) внешнего электрического поля в вакууме к модулю напряженности (vec{E}) полного поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества (varepsilon).
[varepsilon=dfrac{vec{E}_0}{vec{E}}]
Электроемкостью системы из двух проводников называется физическая величина, определяемая как отношение заряда (q) одного из проводников к разности потенциалов (Delta varphi) между ними:
[fbox{$C=dfrac{q}{Delta varphi}$}]
Единицы измерения: (displaystyle [text{Ф}]) (фарад).
Величина электроемкости зависит от формы и размеров проводников и от свойств диэлектрика, разделяющего проводники.
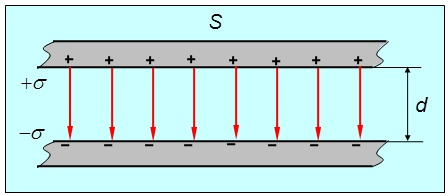
Существуют такие конфигурации проводников, при которых электрическое поле оказывается сосредоточенным (локализованным) лишь в некоторой области пространства. Такие системы называются конденсаторами, а проводники, составляющие конденсатор, — обкладками.
Плоский конденсатор — система из двух плоских проводящих пластин, расположенных параллельно друг другу на малом по сравнению с размерами пластин расстоянии и разделенных слоем диэлектрика.
Электроемкость плоского конденсатора
Разность потенциалов (Delta varphi) между пластинами в однородном электрическом поле равна (Ed), где (d) — расстояние между пластинами. Из этих соотношений можно получить формулу для электроемкости плоского конденсатора:
[C=dfrac{q}{Delta varphi}=dfrac{sigma S}{Ed}=dfrac{varepsilon_0S}{d}]
Таким образом, электроемкость плоского конденсатора прямо пропорциональна площади пластин (обкладок) и обратно пропорциональна расстоянию между ними. Если пространство между обкладками заполнено диэлектриком, электроемкость конденсатора увеличивается в (varepsilon) раз:
[fbox{$C=dfrac{varepsilon_0varepsilon S}{d}$}]
Электрическое поле плоского конденсатора в основном локализовано между пластинами; однако, вблизи краев пластин и в окружающем пространстве также возникает сравнительно слабое электрическое поле, которое называют полем рассеяния. В целом ряде задач приближенно можно пренебрегать полем рассеяния и полагать, что электрическое поле плоского конденсатора целиком сосредоточено между его обкладками.
Последовательное и параллельное соединение конденсаторов
Для достижения нужной емкости или при напряжении, превышающем номинальное напряжение, конденсаторы, могут соединяться последовательно или параллельно. Любое же сложное соединение состоит из нескольких комбинаций последовательного и параллельного соединений.
-
Последовательное соединение конденсаторов
При последовательном соединении, конденсаторы подключены таким образом, что только первый и последний конденсатор подключены к источнику тока одной из своих пластин. Заряд одинаков на всех пластинах, но внешние заряжаются от источника, а внутренние образуются только за счет разделения зарядов ранее нейтрализовавших друг друга. При этом заряд конденсаторов в батарее меньше, чем, если бы каждый конденсатор подключался бы отдельно. Следовательно, и общая емкость батареи конденсаторов меньше.
Напряжение на данном участке цепи соотносятся следующим образом:
[fbox{$U=U_1+U_2$}]
Зная, что напряжение конденсатора можно представить через заряд и емкость, запишем:
[dfrac{q}{C}=dfrac{q}{C_1}+dfrac{q}{C_2}]
Сократив выражение на (Q), получим формулу:
[fbox{$dfrac{1}{C}=dfrac{1}{C_1}+dfrac{1}{C_2}$}]
Откуда эквивалентная емкость батареи конденсаторов соединенных последовательно:
[fbox{$C=dfrac{C_1C_2}{C_1+C_2}$}]
-
Параллельное соединение конденсаторов
При параллельном соединении конденсаторов напряжение на обкладках одинаковое, а заряды разные.
Величина общего заряда полученного конденсаторами, равна сумме зарядов всех параллельно подключенных конденсаторов. В случае батареи из двух конденсаторов:
[fbox{$q=q_1+q_2$}]
Так как заряд конденсатора
[q=CU]
А напряжения на каждом из конденсаторов равны, получаем следующее выражение для эквивалентной емкости двух параллельно соединенных конденсаторов
[CU=C_1U+C_2U]
[fbox{$C=C_1+C_2$}]
-
По сути, расчет общей емкости конденсаторов схож с расчетом общего сопротивления цепи в случае с последовательным или параллельным соединением, но при этом, зеркально противоположен.
Энергия заряженного конденсатора
Заряженный конденсатор обладает энергией. В этом можно убедиться на опыте. Если зарядить конденсатор и замкнуть его на лампочку, то (при условии того, что ёмкость конденсатора достаточно велика) лампочка ненадолго загорится. Следовательно, в заряженном конденсаторе запасена энергия, которая и выделяется при его разрядке.
Вычислим эту энергию: начнём с плоского воздушного конденсатора.
Ответим на такой вопрос: какова силу притяжения его обкладок друг к другу. Величины используем следующие: заряд конденсатора (q), площадь обкладок (S). Возьмём на второй обкладке настолько маленькую площадку, что заряд (q_0) этой площадки можно считать точечным. Данный заряд притягивается к первой обкладке с силой
[F_0 = q_0E_1,]
где (E_1) — напряжённость поля первой обкладки:
[E_1=dfrac{sigma}{2varepsilon_0}=dfrac{q}{2varepsilon_0S}]
Значит
[F_0=dfrac{qq_0}{2varepsilon_0S}]
Направлена эта сила параллельно линиям поля (т.е. перпендикулярно пластинам). Результирующая сила (F) притяжения второй обкладки к первой складывается из всех этих сил (F_0), с которыми притягиваются к первой обкладке всевозможные маленькие заряды (q_0) второй обкладки. При этом суммировании постоянный множитель (displaystyledfrac{q}{2varepsilon_0S}) вынесется за скобку, а в скобке просуммируются все (q_0) и дадут (q). В результате получим
[F=dfrac{q^2}{2varepsilon_0S}]
Предположим теперь, что расстояние между обкладками изменилось от начальной величины (d_1) до конечной величины (d_2). Сила притяжения пластин совершает при этом работу [A = F(d_1 -d_2)]
Знак правильный: если пластины сближаются ((d_2 < d_1)), то сила совершает положительную работу, так как пластины притягиваются друг к другу. Наоборот, если удалять пластины ((d_2 > d_1)), то работа силы притяжения получается отрицательной, как и должно быть.
Получаем
[A=dfrac{q^2}{2varepsilon_0S}(d_1-d_2)=dfrac{q^2d_1}{2varepsilon_0S}-dfrac{q^2d_2}{2varepsilon_0S}=dfrac{q^2}{2C_1}-dfrac{q^2}{2C_2}=W_1-W_2]
Это можно переписать следующим образом: [A =-(W_2-W_1) =-Delta W,]
где [fbox{$W=dfrac{q^2}{2C}$}, (1)]
Работа потенциальной силы (F) притяжения обкладок оказалась равна изменению со знаком минус величины (W). Это как раз и означает, что (W) — потенциальная энергия взаимодействия обкладок, или энергия заряженного конденсатора. Используя соотношение (q = CU), можно получить ещё две формулы для энергии конденсатора (проделать это самостоятельно).
[fbox{$W=dfrac{qU}{2}$}, (2)]
[fbox{$W=dfrac{CU^2}{2}$}, (3)]
Формулы (1)—(3) универсальны: они справедливы как для воздушного конденсатора, так и для конденсатора с диэлектриком.
Содержание книги
Предыдующая страница
§16. Превращение энергии в электрических и магнитных явлениях
В многочисленных электротехнических устройствах происходят постоянные переходы энергии из одной формы в другую. В данном параграфе мы рассмотрим некоторые примеры таких превращений и покажем, что во многих случаях эти переходы связаны с преобразованиями электрических и магнитных полей. Начнем обсуждение этих проблем с устройств, способных накапливать электрический заряд, сохранять его и создаваемое ими электрическое поле в течение длительного промежутка времени.
16.1 Электроемкость.
16.1.1 Электроемкость уединенного проводника.
Любое тело способно накапливать электрический заряд. На первый взгляд, кажется, что любому телу можно сообщить сколь угодно большой заряд. Однако существует ряд причин, которые ограничивают величину максимального заряда. С ростом электрического заряда возрастает напряженность поля, создаваемого телом. Если тело находится в воздухе или другой среде, то может начаться электрический разряд, посредством которого заряд начнет стекать с тела. Даже если рассматриваемое тело находится в вакууме, то электростатическое взаимодействие заряженных частиц внутри вещества приведет к испусканию, эмиссии частиц (чаще всего электронов), что тоже приведет к уменьшению заряда тела. Поэтому необходимо ввести некоторую характеристику тела, описывающую его возможность накапливать электрический заряд. Такой характеристикой является электроемкость тела C : отношение заряда тела к его потенциалу
(~C = frac{Q}{varphi}) . (1)
В этом определении необходимо оговорить, относительно какой точки определяется потенциал. Как правило, для уединенного тела его потенциал отсчитывается относительно бесконечности. Можно дать и несколько иное определение, свободное от указанной неопределенности значения потенциала: электроемкость тела равна заряду, который необходимо сообщить телу, чтобы увеличить его потенциал на единицу
(~C = frac{Delta Q}{Delta varphi}) . (2)
Вспомним другую «емкость»: теплоемкость тела равна количеству теплоты, которое необходимо сообщить телу, чтобы увеличить его температуру на один градус (~C = frac{Delta Q}{Delta t^circ}). Как видите, определение электроемкости полностью аналогично.
Можно дать аналогичное определение емкости сосуда: объем жидкости, который необходимо влить в сосуд, чтобы увеличит высоту его уровня на единицу, то придется признать, что емкость цилиндрического сосуда равна площади его дна (~C = frac{Delta V}{Delta h}). В этом примере аналогом электрического заряда является объем жидкости, налитой в сосуд, аналогом изменения потенциала – изменение уровня жидкости.
Электроемкость является размерной физической величиной. В системе единиц СИ единицей электроемкости является фарад[1] (сокращенно Ф). Емкостью в 1 фарад обладает тело, потенциал которого возрастает на 1 вольт при увеличении его заряда на 1 кулон. Один фарад очень большая емкость, поэтому чаще используются дольные единицы: микрофарад (мкФ, 1 мкФ = 10-6 Ф), нанофарад (нФ, 1 нФ = 10-9 Ф), пикофарад (пФ, 1 пФ = 10-12 Ф).
Для расчета электроемкости следует задать электрический заряд тела и рассчитать его потенциал, после чего вычислить их отношение. Так потенциал тела всегда пропорционален его заряду, то емкость тела не зависит от его заряда, а полностью определяется его размерами, формой и диэлектрическими свойствами среды, в которой находится тело.
Для примера найдем электрическую емкость уединенного шара радиуса R, находящегося в вакууме. Если заряд шара равен Q, то его потенциал (относительно бесконечности) равен
(~varphi = frac{Q}{4 pi varepsilon_0 R}) .
Следовательно, электрическая емкость шара равна
(~C = frac{Q}{varphi} = 4 pi varepsilon_0 R) . (3)
Так электрическая емкость земного шара (R ≈ 6350 км) равна С ≈ 7·10-4 Ф — действительно 1 фарад очень большая емкость.
Если поместить шар в бесконечную среду из однородного диэлектрика с проницаемостью ε, то напряженность поля уменьшится в ε раз, потенциал шара также уменьшится, поэтому его емкость возрастет в ε раз:
(~C = 4 pi varepsilon_0 varepsilon R) . (4)
16.1.2 Конденсаторы.
Мы показали, что уединенные тела малопригодны как накопители электрического заряда. Еще в середине XVIII века было изобретено устройство, способное накапливать и длительное время сохранять большие электрические заряды – конденсатор.
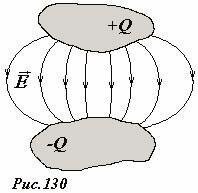
Конденсатор представляет собой два проводника (которые называются обкладками), разделенными диэлектриком (Рис. 130). Как правило, на обкладки подают разноименные электрические заряды, равные по величине. В этом случае электрическое поле практически полностью локализуется в пространстве между обкладками. Емкостью конденсатора называется отношение заряда одной из обкладок к разности потенциалов между обкладками
(~C = frac{Delta Q}{Delta varphi}) . (5)
В этом определении фигурирует разность потенциалов, которая не зависит от выбора нулевого уровня потенциала, поэтому нет необходимости в дополнительных оговорках. Часто зарядом конденсатора называют заряд одной из его обкладок (ясно, что полный заряд конденсатора на двух обкладках равен нулю), вместо разности потенциалов между обкладками чаще говорят о напряжении конденсатора U, которое, конечно, равно разности потенциалов U = Δϕ, так в пространстве между обкладками не действуют сторонние силы.
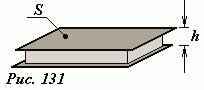
Простейший конденсатор состоит из двух проводящих параллельных пластин, разделенных слоем диэлектрика, причем расстояние между пластинами значительно меньше их размеров – такой конденсатор называется плоским (Рис. 131). Найдем емкость такого конденсатора. Будем считать, что на обкладки конденсатора (проводящие пластины) поданы разноименные электрические заряды, модули которых равны Q. Если площадь каждой пластины равна S , то поверхностная плотность заряда на них равна (~sigma = frac{Q}{S}). Эти заряды создают в пространстве между пластинами электрическое поле напряженности (~E = frac{sigma}{varepsilon varepsilon_0} = frac{Q}{varepsilon varepsilon_0 S}), где ε — диэлектрическая проницаемость вещества между пластинами. Разность потенциалов между обкладками конденсатора равна (~Delta varphi = Eh = frac{Qh}{varepsilon varepsilon_0 S}). По определению емкость плоского конденсатора рассчитывается по формуле
(~C = frac{Q}{Delta varphi} = frac{varepsilon varepsilon_0 S}{h}) . (6)
Таким образом, емкость конденсатора пропорциональна проницаемости диэлектрика, площади пластин и обратно пропорциональна расстоянию между ними. Если расстояние между пластинами сделать малым, а площади пластин большими, то такой конденсатор может иметь большую емкость (даже превосходящую емкость земного шара).
Конденсаторы широко используются не только для накопления электрического заряда, но и в цепях переменного электрического тока (эти вопросы мы рассмотрим позднее). На электрических схемах конденсаторы изображаются в виде двух параллельных отрезков (Рис. 132).
Промышленностью выпускаются конденсаторы различных типов, которые различаются своей конструкцией. Емкости промышленно выпускаемых конденсаторов изменяются в широких пределах от нескольких пикофарад, до единиц фарад. Часто пластины таких конденсаторов изготавливают из тонкой металлической фольги, которую скручивают в рулоны и помещают в корпус. В качестве диэлектрика используется воздух (в этом случае с высокой точностью можно считать ε = 1), слюда, сухая бумага, и другие материалы.
Большой электрической емкостью обладают электролитические конденсаторы. Одной обкладкой такого конденсатора служит тонкая полоска фольги большой площади, покрытая слоем окисла (который играет роль диэлектрика), второй обкладкой является раствор электролита. Так как толщина оксидного слоя может быть малой (порядка нескольких микрон), то емкость такого конденсатора весьма велика. При использовании таких конденсаторов следует внимательно следить за полярностью их включения в электрическую цепь, так как при ошибочном подключении оксидный слой быстро разрушается, что приводит к выходу конденсатора из строя.
Широко используются также конденсаторы переменной емкости, в котором наборы пластин могут двигаться друг относительно друга, при этом изменяется площадь их перекрытия, вследствие чего изменяется и емкость конденсатора. На схемах переменные конденсаторы отмечаются стрелкой (Рис. 132б).
16.1.3 Соединение конденсаторов.
Установим правила для расчета электроемкости системы конденсаторов, подобно правилам расчета сопротивлений соединенных резисторов.
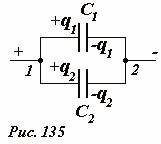
При параллельном соединении конденсаторов (Рис. 135) емкости которых равны C1 и C2 напряжения на обоих конденсаторах одинаковы и равны разности потенциалов между точками соединения U1 = U2 = Δϕ, что является следствием потенциальности электростатического поля. Суммарный заряд конденсатора равен сумме зарядов конденсаторов q = q1 + q2.
По определению емкость такого составного конденсатора равна отношению его суммарного заряда к напряжению, следовательно,
(~C = frac{q_1 + q_2}{U} = frac{q_1}{U} + frac{q_2}{U} = C_1 + C_2) . (1)
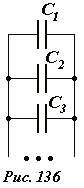
Это правило легко обобщается: общая емкость системы параллельно соединенных конденсаторов (Рис. 136) равна сумме емкостей всех конденсаторов
(~C_o = C_1 + C_2 + C_3 + ldots = sum_k C_k) . (2)
В частном случае плоских конденсаторов с одинаковыми расстояниями между пластинами установленное правило утверждает, что суммарная площадь пластин равна сумме площадей отдельных обкладок
(~S_o = S_1 + S_2 + S_3 + ldots) .
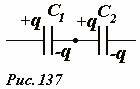
При последовательном соединении конденсаторов (Рис. 137) суммарное напряжение на батарее конденсаторов равно сумме напряжений на отдельных конденсаторах
(~U_o = U_1 + U_2) . (3)
Электрические заряды на всех конденсаторах одинаковы
(~q_o = q_1 = q_2) .
Для доказательства этого утверждения достаточно рассмотреть две соединенных внутренних обкладки, которые изолированы от внешних источников – их суммарный заряд остается равным нулю. Поэтому если на обкладке первого конденсатора индуцируется заряд − q, то на соединенной с ней обкладке второго конденсатора возникнет такой же по модулю заряд противоположного знака.
Выразим напряжения на конденсаторах через их заряды и емкости (~U = frac{q}{C}) и подставим их в уравнение (3)
(~frac{q_o}{C_o} = frac{q_1}{C_1} + frac{q_2}{C_2}) ,
принимая во внимание равенство всех зарядов, получим правило расчета емкости последовательно соединенных конденсаторов (Рис. 138):
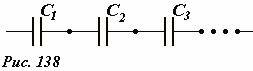
величина обратная емкости батареи последовательно соединенных конденсаторов равна сумме величин, обратных емкости каждого конденсатора,
(~frac{1}{C_o} = frac{1}{C_1} + frac{1}{C_2} + frac{1}{C_3} + ldots = sum_k frac{1}{C_k}) . (4)
Для плоских конденсаторов с одинаковыми площадями пластин это правило утверждает, что суммарное расстояние между пластинами равно сумме этих расстояний всех конденсаторов.
Интересно отметить, что правила расчетов емкости батареи конденсаторов противоположны правилам расчета сопротивлений соединений резисторов: при последовательном соединении складываются сопротивления; при параллельном – складываются величины обратные сопротивлениям (проводимости), а для конденсаторов наоборот: при параллельном соединении складываются емкости, а при последовательном – складываются обратные величины.
Примечания
- ↑ Названа в честь выдающегося английского физика Майкла Фарадея.
Следующая страница
Одним из важных параметров, учитываемых в электрических цепях, является электрическая емкость – способность проводников накапливать заряды. Понятие емкости применяется как для уединенного проводника, так и для системы, состоящей из двух и более проводников. В частности, емкостью обладают конденсаторы, состоящие из двух металлических пластин, разделенных диэлектриком или электролитом.
Для накопления зарядов широко применяютсяаккумуляторы, используемые в качестве источников постоянного тока для питания различных устройств. Количественной характеристикой, определяющей время работы аккумулятора, является его электроемкость.
Определение
Если диэлектрик, например, эбонитовую палочку, наэлектризовать трением то электрические заряды сконцентрируются в местах соприкосновения с электризующим материалом. При этом, другой конец палочки можно насытить зарядами противоположно знака и такая наэлектризованность будет сохраняться.
Совсем по-другому ведут себя проводники, помещенные электрическое поле. Заряды распределяются по их поверхности, образуя некий электрический потенциал. Если поверхность ровная, как у палочки, то заряды распределятся равномерно. Под действием внешнего электрического поля в проводнике происходит такое распределение электронов, чтобы внутри его сохранялся баланс взаимной компенсации негативных и позитивных зарядов.
Внешнее электрическое поле притягивает электроны на поверхность проводника, компенсируя при этом положительные заряды ионов. По отношению к проводнику имеет место электростатическая индукция, а заряды на его поверхности называются индуцированными. При этом на концах проводника плотность зарядов будет несколько выше.
На металлическом шаре заряды распределяются равномерно по всей поверхности. Наличие полости любой конфигурации абсолютно не влияет на процесс распределения.
Однако, если проводник убрать из зоны действия поля, то его заряды перераспределятся таким образом, что он снова станет электрически нейтральным.
На рисунке 1 изображена схема заряженного разнополюсного диэлектрика и проводника, удалённого из зоны действия электростатического поля. Благодаря тому, что диэлектрик сохраняет полученные заряды, уединенный проводник восстановил свою нейтральность.
Интересное явление наблюдается с двумя проводниками, разделенными диэлектриком. Если одному из них сообщить положительный заряд, а другому – отрицательный, то после убирания источника электризации заряды на поверхности проводников сохранятся. Заряженные таким образом проводники обладают разностью потенциалов.
Заряды, накопившиеся на диэлектрике, уравновешивают внутренние взаимодействие в каждом из проводников, не позволяя им разрядиться. Величина заряда зависит от площади поверхности параллельных проводников и от свойства диэлектрика, расположенного между ними.
Свойство сохранять накопленный заряд называется электроемкостью. Точнее говоря, – это характеристика проводника, физическая величина определяющая меру его способности в накоплении электрического заряда.
Накопленное электричество можно снять с проводников путем короткого замыкания их или через нагрузку. С целью увеличения емкости на практике применяют параллельные пластины или же длинные полоски тонкой фольги, разделённой диэлектриком. Полоски сворачивают в тугой цилиндр для уменьшения объема. Такие конструкции называют конденсаторами.
На рисунке 2 изображена схема простейшего конденсатора с плоскими обкладками.
Существуют конденсаторы других типов:
- переменные;
- электролитические;
- оксидные;
- бумажные;
- комбинированные и другие.
Важной характеристикой конденсатора, как и других накопительных систем, является его электрическая емкость.
Формулы
На рисунке 3 наглядно показано формулы для определения емкости, в т. ч. и для сферы.
По отношению к конденсатору, для определения его емкости применяют формулу: C = q/U. То есть, эта величина прямо пропорциональна заряду одной из обкладок и обратно пропорциональна разнице потенциалов между обкладками (см. рис. 4).
О других способах определения ёмкости конденсатора читайте в нашей статье: https://www.asutpp.ru/kak-opredelit-emkost-kondensatora.html
Единицы измерения
За единицу измерения величины электроемкости принято фараду: 1 Ф = 1 Кл/1В. Поскольку фарада величина огромная, то для измерения емкости на практике она мало пригодна. Поэтому используют приставки:
- мили (м) = 10-3;
- микро (мк) = 10-6;
- нано (н) = 10-9;
- пико (пк) = 10-12;
Например, электрическая емкость 1 мкф = 0,000001 Ф. Параметр зависит от геометрических размеров, конфигурации проводника и материала диэлектрика.
Уединенный проводник и его емкость
Уединенным называют проводник, влиянием на который других элементов цепей можно пренебречь. Предполагается, что все другие проводники бесконечно удалены от него, а как известно, потенциал точки, бесконечно удаленной в пространстве, равен 0.
Электрическую емкость C уединенного проводника, определяют как количество электричества q, которое требуется для повышения электрического потенциала на 1 В: С = q/ϕ. Параметр не зависит от материала, из которого изготовлен проводник.
Конденсаторы постоянной и переменной емкости
Эра накопителей электричества началась с воздушных конденсаторов. Благодаря плоскому конденсатору с большой площадью обкладок физики смогли понять, как взаимная емкость регулируется площадями пластин, что позволило им создать конденсаторы с переменной емкостью (см. рис. 5).
Идея изменения емкости состояла в том, чтобы путем поворота плоской обкладки изменять площадь поверхности, которая располагается напротив другой пластины. Если обкладки располагались точно друг против друга, то напряженность поля между ними была максимальной. При смещении одной из пластин на некоторый угол, напряженность уменьшалась, что приводило к изменению емкости. Таким образом, можно было плавно управлять накопительной способностью конденсатора.
Детали с переменной емкостью нашли применение в первых радиоприемниках для поиска частоты нужной станции. Данный принцип используется по сегодняшний день в различных аналоговых электрических схемах.
Большую популярность приобрели электролитические конденсаторы. В качестве одной из обкладок у них используется электролит, обладающий высокими показателями диэлектрической проницаемости. Благодаря диэлектрическим свойствам электролитов такие конденсаторы обладают большими емкостями.
Главные их преимущества электролитического конденсатора:
- высокие
показатели емкости при малом объеме; - применение в
цепях с постоянным током.
Недостатки:
- необходимо соблюдать полярность;
- ограниченный срок службы;
- чувствительность к повышенным напряжениям.
Высокую электрическую прочность имеют плоские конденсаторы, у которых в качестве диэлектрического материала применяется керамика. Они используются в цепях с переменным током и выдерживают большие напряжения.
Сегодня промышленность поставляет на рынок множество конденсаторов различных типов, с высокими показателями проницаемости диэлектриков.
Аккумуляторы и электроемкость
Накопители электричества большой емкости (аккумуляторы) состоят из положительных и негативных пластин, погруженных в электролит. Во время зарядки часть атомов электролита распадается на ионы, которые оседают на пластине. Образуется разность потенциалов между пластинами, что является причиной возникновения ЭДС при подключении нагрузки.
С целью увеличения напряжения аккумуляторы последовательно соединяют в батареи. Разница потенциалов одной секции около 2 В. Для получения аккумулятора на 6 В необходимо создать батарею из трех секций, а на 12 В – батарею из 6 секций.
Для характеристики аккумуляторов (батарей) используются параметры:
- емкости;
- номинального напряжения;
- максимального тока разряда.
Единицей емкости аккумулятора является ампер-час (А*ч) или кратные ей миллиампер-часы (мА*ч). Емкость аккумулятора зависит от площади пластин. Увеличить емкость можно путем параллельного подключения нескольких секций, но такой способ почти не применяется, так как проще и надежнее создать аккумулятор с большими пластинами.
Если двум, находящимся на некотором расстоянии друг от друга, проводникам сообщить электрические заряды (q1 и q2), между ними появится электрическое поле. Разность потенциалов (Δφ) в нём будет определяться величинами сообщённых зарядов и формой, которую имеют проводники. Разность потенциалов между 2 точками постоянного во времени и однородного электрического поля называют напряжением (U).
Заряды, сообщённые проводникам, могут быть оба положительными, оба отрицательными или иметь разные знаки. Последний случай при равных абсолютных значениях зарядов нашёл в физике и электротехнике наибольшее применение и поэтому нам особенно интересен.
Электроемкость
Определение 1
Под конденсатором понимают систему из нескольких (чаще всего двух) находящихся близко друг от друга проводников, отделённых друг от друга слоем диэлектрика.
В подавляющем большинстве случаев его толщина много меньше размеров обкладок.
Определение 2
Электрической ёмкостью (C) между двумя проводниками называется скалярная величина, прямо пропорциональная абсолютной величине заряда одного из проводников и обратно пропорциональная разности потенциалов и напряжению между ними.
В виде формулы данное определение можно записать следующим образом:
[C=(q / Delta varphi)=(q / U)]
В системе СИ электроёмкость измеряют в Фарадах. Один Фарад равен электроемкости конденсатора, при которой заряд, равный 1 Кулону, создаёт между его пластинами напряжение в 1 Вольт.
[1 Phi=frac{1 mathrm{~Kл}}{1 mathrm{~B}}]
Ёмкость в 1 Фарад – величина очень большая. На практике чаще всего используют мили фарады (одна тысячная фарада), микрофарады (одна миллионная), нанофарады (одна миллиардная), пикофарады (10 в минус 12-й степени).
Определение 3
Плоским называют конденсатор, образованный двумя плоскими, параллельно расположенными по отношению друг к другу пластинами. Если роль диэлектрика между ними играет воздух, то такой конденсатор называют воздушным.
Определение 4
Электрическое поле в плоском конденсаторе сосредотачивается главным образом между пластинами, однако часть его выходит за их пределы. Это вышедшее поле называют полем рассеяния. Оно не является потенциальным, т.е. работа при перемещении в нём заряда из одного места в другое не равна нулю.
Обычно такое поле не велико и при решении многих (но далеко не всех) задач его наличием можно пренебречь.
Абсолютную величину напряжённости каждой из обкладок можно выразить формулой:
[E_{1}=frac{sigma}{2 varepsilon_{0}}].
Где σ это плотность электрического заряда на плоскости. По принципу суперпозиции полная величина напряжённости поля конденсатора равна сумме напряжённостей полей от каждой из его обкладок.
[vec{E}=overrightarrow{E^{+}}+overrightarrow{E^{-}}]
Т. к. между пластинами векторы [overrightarrow{E^{+}} text {и } overrightarrow{E^{-}}] параллельны, полную напряжённость можно вычислить по формуле [E=2 E_{1}=frac{sigma}{varepsilon_{0}}].
Вне пластин поля каждой из них компенсируют друг друга, и потому общая их напряжённость равна нулю.
Как вычислить электроемкость плоского конденсатора
Вспомним, как ёмкость зависит от заряда пластин и разности потенциалов между ними. Это формула [mathrm{C}=(mathrm{q} / Delta varphi) . text { Заряд } mathrm{q}=sigma * mathrm{~S}, mathrm{~S}] – площадь одной обкладки.
Разность потенциалов в однородном электростатическом поле равна напряжению и вычисляется по формуле [Delta varphi=mathrm{E}^{*} mathrm{~d}]
Подставляем эти значения в формулу для ёмкости. В результате получаем:
[C=left(sigma^{*} Sright) /left(E^{*} dright)]
Т. к. электрическая постоянная ε0 равна σ/E в итоге получаем [C=frac{q}{Delta varphi}=frac{sigma cdot S}{E cdot d}=frac{varepsilon_{0} S}{d}].
Теперь давайте определим электроемкость конденсатора в форме сферы и цилиндра.
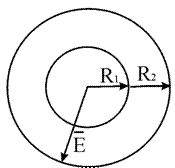
Сферический конденсатор
Определение 5
Им называют систему двух проводящих, расположенных одна в другой сфер с радиусами R1 и R2. Будем исходить из того, что они имеют общий центр.
[varphi_{1}-varphi_{2}=int E d x=int frac{k Q d r}{r^{2}}=k Qleft(frac{1}{R_{1}}-frac{1}{R_{2}}right)] т. к. [C_{c Phi}=frac{Q}{k Qleft(frac{1}{R_{1}}-frac{1}{R_{2}}right)}=frac{4 pi varepsilon varepsilon_{0} R_{1} R_{2}}{R_{2}-R_{1}}]
У нас R2 -R1 << R1. Это значит, что R1 и R2 можно принять равными R, тогда произведение радиусов в формуле можно будет считать квадратом R.
R2 – R1=d
Исходя из того что [C_{c Phi}=frac{4 pi varepsilon varepsilon_{0} R^{2}}{d}] и [S_{c Phi}=4 pi R^{2}].
В итоге получаем [C=frac{varepsilon varepsilon_{0} S}{d}=frac{4 pi varepsilon varepsilon_{0} R^{2}}{R_{2}-R_{1}}].
Цилиндрический конденсатор
Определение 6
Им называют систему находящихся один в другом цилиндров.
Для упрощения расчётов расположим их на одной оси.
Если пренебречь краевыми эффектами, то [varphi_{1}-varphi_{2}=frac{lambda}{2 pi varepsilon varepsilon_{0}} ln left(frac{r_{2}}{r_{1}}right)=frac{q}{2 pi varepsilon varepsilon_{0} l} ln left(frac{r_{2}}{r_{1}}right)]
[C=frac{q}{varphi_{1}-varphi_{2}}=frac{2 pi varepsilon_{0}}{ln left(frac{r_{2}}{r_{1}}right)}].
Теперь вы знаете, чему равна электроемкость конденсатора, давайте рассмотрим их соединения в электрической цепи.
Нет времени решать самому?
Наши эксперты помогут!
Расчёт электроемкости батареи конденсаторов
Определение 7
Батареей статических конденсаторов называют группу конденсаторов, связанных между собой электрическим соединением.
У параллельно соединённых конденсаторов одинакова разность потенциалов между обкладками Q1= С1 (φА- φВ), Q2= С2 (φА- φВ), Q3 = С3 (φА- φВ). Заряд батареи складывается из зарядов каждого из отдельных конденсаторов, в неё входящих. Поэтому легко понять почему
[Q=sum_{i-1}^{N} Q_{i}=sum_{i=1}^{N} C_{i}left(varphi_{mathrm{A}^{-}} varphi_{mathrm{B}}right)]
Суммарная ёмкость батареи при таком раскладе равна
[C_{text {парал }}=frac{Q}{varphi_{A}-varphi_{B}}=sum_{i=1}^{N} C_{i}]
Выходит, что при параллельном соединении ёмкости просто складываются.
При последовательном соединении конденсаторов ситуация будет совершенно другой.
В этом случае заряды обкладок всех входящих в батарею конденсаторов равны по абсолютной величине. Разность потенциалов на её концах равняется сумме разностей потенциалов на каждом из них. В виде формулы можно записать таким образом Dj=Dj1 + Dj2 + ….+ Dj.
Для каждого из конденсаторов батареи справедливы соотношения:
[Delta varphi_{mathrm{i}}=mathrm{q} / mathrm{C}_{mathrm{i}}, text { но } Delta varphi=mathrm{Q} / mathrm{C}=mathrm{Q} sum_{i=1}^{N} frac{1}{C_{i}} mathrm{p}]
[frac{1}{C_{text {посл }}}=Q sum_{i=1}^{N} C_{i}].
Из этого следует однозначный вывод, что при последовательном соединении ёмкость батареи всегда меньше ёмкости любого из её конденсаторов.
Электроемкость конденсатора колебательного контура
Определение 8
Колебательным контуром называют электрическую цепь, содержащую конденсатор, катушку индуктивности и источник электричества.
Мы для вычисления ёмкости будем рассматривать упрощённую его схему, состоящую только из конденсатора и катушки. Сопротивление соединяющих их проводников положим равным нулю. Сопротивлением катушки и излучением электромагнитных волн тоже пренебрегаем. Такой контур называют идеальным.
Придадим обкладкам конденсатора заряды –Q и +Q. В начальный момент времени электроемкость конденсатора контура будет [W_{C}=frac{Q^{2}}{2 C}].
Это максимальное значение ёмкости конденсатора в контуре. Выше него никак не будет.
Если замкнуть конденсатор на катушку, он начнёт разряжаться, возникнет электрический ток. В катушке появится и станет возрастать магнитное поле. В максимуме, когда конденсатор полностью разрядится, энергия порождённого током поля будет [W_{L}=frac{1}{2} L I^{2}].
Полная энергия системы останется постоянной и равна [W_{text {полн}}=frac{1}{2}left(frac{Q^{2}}{C}+L I^{2}right)=mathrm{const}].
Электроемкость конденсатора, энергия которого известна, из приведённых формул вычисляется достаточно легко:
C=Q2/(2W-LI2)
В контуре станут происходить гармонические колебания, общее их уравнение [ddot{Q}+frac{1}{L C} Q=0].
Его решение: [Q(t)=Q_{m} cos omega_{0} t]
Для силы тока и напряжения получим
[I=frac{d Q}{d t}=-omega_{0} Q_{m} sin omega_{0} t=I_{m} cos left(omega_{0} t+frac{pi}{2}right)], [U_{C}=frac{Q}{C}=frac{Q_{m}}{C} cos omega_{0} t=U_{m} cos omega_{0} t].
Чтобы получить формулу электроемкости конденсатора колебательного контура в любой момент времени, следует обе части
[U_{C}=frac{Q}{C}=frac{Q_{m}}{C} cos omega_{0} t]
Умножить на C и поделить на Uc.
В результате получим: [C=frac{Q_{m}}{U_{C}} cos omega_{0} t].