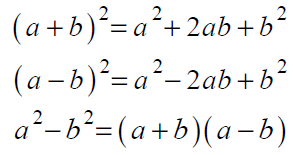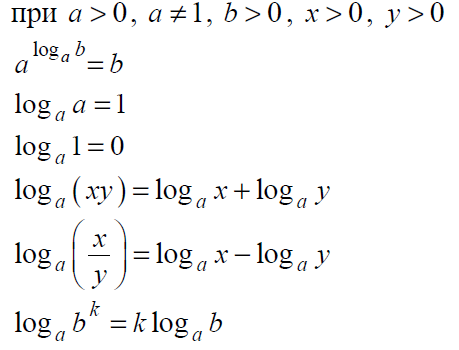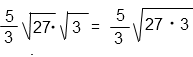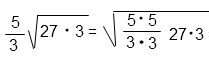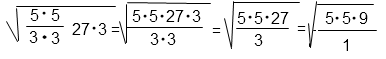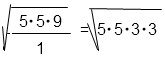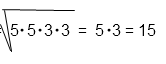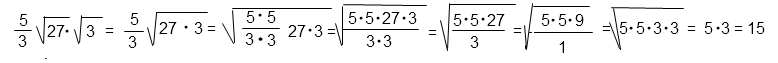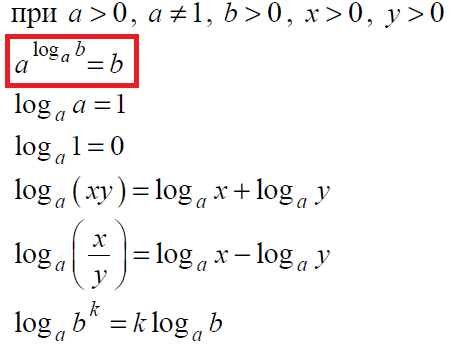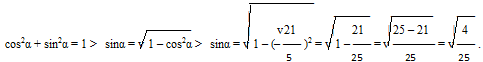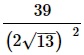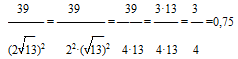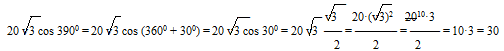Егэ по математике как найдите значение выражения - AvtoShod.ru

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения $frac{2,88cdot 44,5}{0,288cdot 4,45}.$

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

$frac{2,88cdot 44,5}{0,288cdot 4,45}=frac{2,88cdot 44,5}{2,88cdot 0,445}=frac{44,5}{0,445}=100.$

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения $7frac{9}{13}:frac{5}{13}.$

$7frac{9}{13}:frac{5}{13}=frac{100}{13}cdot frac{13}{5}=20.$

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

$left ( sqrt{a} right )^{2}=a;;sqrt{a}geq 0;;ageq 0$ .

3. Вычислите .

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:

Упростим множители:

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7} right )^{2}+2sqrt{3}cdot sqrt{7}+left ( sqrt{3} right )^{2}}=$

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7}+sqrt{3}right )^{2}}=2left ( sqrt{7}-sqrt{3} right )left ( sqrt{7}+sqrt{3} right )=$

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

$a^{m}cdot a^{n}=a^{m+n}.$

$frac{a^{m}}{a^{n}}=a^{m-n}.$

$left ( a^{m} right )^{n}=left ( a^{n} right )^{m}=a^{mn}.$

$a^{n}b^{n}=left ( ab right )^{n}.$

$frac{a^{n}}{b^{n}}=left ( frac{a}{b} right )^{n}.$

5. Найдите значение выражения: $frac{a^{8,9}}{a^{4,9}}$ при a=4.

$frac{a^{8,9}}{a^{4,9}}=a^{8,9-4,9}=a^{4}=4^{4}=256.$

Применили формулу частного степеней $frac{a^{m}}{a^{n}}=a^{m-n}.$

Ответ: 256.

6. Вычислите $left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}.$

$left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}=left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{2^{frac{1}{12}}} right )^{2}=left ( 2^{frac{1}{3}+frac{1}{4}-frac{1}{12}} right )^{2}=left ( 2^{frac{4}{12}+frac{3}{12}-frac{1}{12}} right )^{2}=$

$=left (2^{frac{1}{2}} right )^{2}=2.$

Ответ: 2.

7. Вычислите $frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}$ , если .

Спокойно, не пугаемся. И конечно, не спешим подставлять значение m=3,7. Сначала упростим выражение.

$frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}=frac{5m^{30}+13m^{30}}{4m^{30}}=frac{18m^{30}}{4m^{30}}=4,5.$

Ответ: 4,5.

8. Вычислите $0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}.$

$0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}=left ( frac{3}{4} right )^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot left ( 3cdot 4 right )^{frac{7}{8}}=frac{3^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 3^{frac{7}{8}}cdot 4^{frac{7}{8}}}{4^{frac{1}{8}}}=3cdot 4=12.$

Применили формулу для произведения степеней: $a^{m}cdot a^{n}=a^{m+n}.$

Ответ: 12.

9. Вычислите $frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}.$

$frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}=frac{3^{frac{1}{28}}cdot 3cdot 3^{frac{1}{21}}}{3^{frac{1}{12}}}=3^{frac{1}{28}+1+frac{1}{21}-frac{1}{12}}=3^{frac{3}{84}+1+frac{4}{84}-frac{7}{84}}=3.$

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

$log _{a}b=cLeftrightarrow a^{c}=b$ .

При этом > 0, > 0, aneq 1.

Основные логарифмические формулы:

Основное логарифмическое тождество: $boldsymbol{log _{a}a^{c}=c, ; a^{log _{a}b}=b}.$

Логарифм произведения равен сумме логарифмов: $boldsymbol{log _{a}left ( bc right )=log _{a}b+log _{a}c}.$

Логарифм частного равен разности логарифмов: $boldsymbol{log _{a}left ( frac{b}{c} right )=log _{a}b-log _{a}c}.$

Формула для логарифма степени: $boldsymbol{log _{a}b^{m}=mlog_{a}b}.$

Формула перехода к новому основанию: $boldsymbol{log _{a}b=frac{1}{log _{b}a},; log _{a}b=frac{log _{c}b}{log _{c}a}}.$

10. Вычислите: $log _{5}7cdot log _{7}25$ .

$log _{5}7cdot log _{7}25=log _{5}7cdot log _{7}5^{2}=2log _{5}7cdot log _{7}5=2.$

Снова формула перехода к другому основанию.

$log _{a}b=frac{1}{log _{b}a}$ , поэтому
$log _{a}bcdot log _{b};a=1.$

11. Найдите $log _{a}frac{a^{6}}{b^{4}}$ , если $log _{a}b=-2$ .

$log _{a}frac{a^{6}}{b^{4}}=log _{a}a^{6}-log _{a}b^{6}=6-4log _{a}b=6-4cdot left ( -2 right )=6+8=14.$

12. Найдите значение выражения $frac{log _{2}80}{3+log _{2}10}$ .

$frac{log _{2}80}{3+log _{2}10}=frac{log _{2}left (8cdot 10 right )}{3+log _{2}10}=frac{log _{2}8+log _{2}10}{3+log _{2}10}=frac{3+log _{2}10}{3+log _{2}10}=1.$

13. Найдите значение выражения $frac{log _{9}sqrt[10]{8}}{log _{9}8}$ .

$frac{log _{9}sqrt[10]{8}}{log _{9}8}=frac{log _{9}8^{frac{1}{10}}}{log _{9}8}=frac{1}{10}=0,1$ .

14. Найдите значение выражения $left ( 1-log _{3}18 right )left ( log _{6}54 -1right )$ .

$left ( 1-log _{3}18 right )left ( log _{6}54 -1right )=-left ( log _{3}18-log _{3}3 right )cdot left ( log _{6}54-log _{6}6 right )=-log _{3}6cdot log _{6}9=-2log _{3}6cdot log _{6}3=-2.$

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите: $44sqrt{3}tgleft ( -480^{circ} right ).$

$44sqrt{3}tgleft ( -480^{circ} right )=44sqrt{3}cdot frac{sin left ( -480^{circ} right )}{cos left ( -480^{circ} right )}=-44sqrt{3}cdot frac{sin 480^{circ}}{cos 480^{circ}}=-44sqrt{3}cdot frac{sin 120^{circ}}{cos 120^{circ}}=-44sqrt{3}cdot frac{sqrt{3}}{2}:left ( -frac{1}{2} right )=132.$

16. Найдите , если $sin alpha =-frac{2sqrt{2}}{3}$ и $alpha in left ( frac{3pi }{2};;2pi right )$ .

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{2sqrt{2}}{3} right )^{2}=1-frac{8}{9}=frac{1}{9}.$

Т.к. $alpha in left ( frac{3pi }{2};;2pi right )$ , то $cos alpha =frac{1}{3}.$
$3cos alpha =3cdot frac{1}{3}=1.$

17. Найдите , если $sin alpha =-frac{1}{sqrt{5}}$ и

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{1}{sqrt{5}} right )^{2}=1-frac{1}{5}=frac{4}{5}.$

Т.к. , то
$cos alpha =frac{2}{sqrt{5}}.$

$tgalpha =frac{sin alpha }{cos alpha }=-frac{1}{sqrt{5}}:frac{2}{sqrt{5}}=-2.$

18. Найдите значение выражения: $frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}.$

$frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{13cdot 2sin 76^{circ}cdot cos 76^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{26sin 76^{circ}}{cos 14^{circ}}=frac{26sin left ( 90^{circ}-14^{circ} right )}{cos 14^{circ}}=$

$=frac{26cos 14^{circ}}{cos 14^{circ}}=26.$

Применили формулу приведения.

19. Упростите выражение: $frac{3cos(pi - beta)+sin(frac{pi}{2}+beta)}{cos(beta+3pi)}.$

$frac{3cos left ( pi -beta right )+sin left ( frac{pi }{2}+beta right )}{cos left ( beta +3pi right )}=frac{-3cos beta +cos beta }{-cos beta }=frac{-2cos beta }{-cos beta }=2.$

Применили формулу приведения.

20. Найдите , если .

$2cos 2alpha =2left ( 1-2sin ^{2}alpha right )=2-4sin ^{2}alpha =2-4cdot left ( -0,7 right )^{2}=0,04.$

21. Вычислите $frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }$ , если

$frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }=frac{1-cos ^{2}alpha +sin ^{2}alpha +2sin alpha cos alpha }{1+cos ^{2}alpha -sin ^{2}alpha +2sin alpha cos alpha }=$

$=frac{2sin ^{2}alpha +2sin alpha cos alpha }{2cos ^{2}alpha +2sin alpha cos alpha }=frac{sin alpha left ( sin alpha +cos alpha right )}{cos alpha left ( cos alpha +sin alpha right )}=frac{sin alpha }{cos alpha }=tgalpha =0,3.$

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти $sqrt{a^{2}}$ .

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}$ при .

Запомним: $sqrt{a^{2}}=left | a right |.$

$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}=left | a-2 right |+left | a-4 right |$ .

Если , то и .

При этом и .

При получаем: .

Ответ: 2.

23. Найдите значение выражения

$x+sqrt{x^{2}-24x+144}$ при xleq 12 .

При xleq 12 получим:

$x+sqrt{x^{2}-24x+144}=x+sqrt{left ( x-12 right )^{2}}=x+left | x-12 right |=x+12-x=12.$

Ответ: 12.

24. Найдите $frac{gleft ( 5-x right )}{gleft ( 5+x right )}$ , если , при .

Что такое ? Это функция, каждому числу ставящая в соответствие число . Например, ;

Тогда:

Заметим, что .

Значит, при
$frac{gleft ( 5-x right )}{gleft ( 5+x right )}=1$ .

25. Найдите $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ , если $pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ , при .

$pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ — функция, каждому числу b ставящая в соответствии число
$left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ .

Тогда при bneq 0.

$pleft ( frac{1}{b} right )=left ( frac{1}{b}-9b right )left ( -frac{9}{b} +bright )=left ( b-frac{9}{b} right )left (-9b +frac{1}{b} right )=pleft ( b right )$ , и значение выражения $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ равно 1.

Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
08.05.2023

Источник

В задании (6) ЕГЭ по профильной математике нужно преобразовать числовое, буквенное, степенное, иррациональное, логарифмическое или тригонометрическое выражение и найти его значение. За это задание можно получить (1) балл.

Пример:

найди значение выражения

−20tg53°⋅tg143°=−20tg53°⋅tg(90°+53°)=−20tg53°⋅ctg53°.

Алгоритм выполнения задания

Определи тип выражения.
Выполни преобразования, соответствующие типу выражения.
Если задано значение переменной, подставь это значение в упрощённое выражение. Вычисли его значение.
Запиши ответ.

Как решить задание из примера?

Дано тригонометрическое выражение.
Заметим, что

143°=90°+53°

. Используем формулу приведения

tg(90+α)=−ctgα

и преобразуем выражение:

−20tg53°⋅tg143°=−20tg53°⋅tg(90°+53°)=−20tg53°⋅ctg53°.
Воспользуемся формулой

tgα⋅ctgα=1

:

−20tg53°⋅ctg53°=−20⋅1=−20.
Запишем ответ (непосредственно в самом задании — без точки в конце).

Ответ: (-20).

Обрати внимание!

В заданиях «Как на ЕГЭ» ответы записывай в виде целого числа или десятичной дроби без пробелов и точки в конце.

Если получилась обыкновенная дробь и её нельзя перевести в конечную десятичную дробь — ищи ошибку в решении!

Источник

СДАМ ГИА:

РЕШУ ЕГЭ

Образовательный портал для подготовки к экзаменам

Математика базового уровня

≡ Математика

Базовый уровень

Профильный уровень

Информатика

Русский язык

Английский язык

Немецкий язык

Французский язык

Испанский язык

Физика

Химия

Биология

География

Обществознание

Литература

История

Сайты, меню, вход, новости

СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ

Об экзамене

Каталог заданий

Варианты

Ученику

Учителю

Школа

Справочник

Сказать спасибо

Вопрос — ответ

Чужой компьютер

Зарегистрироваться

Восстановить пароль

Войти через ВКонтакте

Играть в ЕГЭ-игрушку

Новости

26 мая

Как заработать +20–30 баллов на ЕГЭ благодаря разборам ЕГЭ с Дальнего Востока

24 мая

Обновлённая панель инструментов

22 мая

Беседы Решу ЕГЭ по подготовке к ЕГЭ

11 мая

Решение досрочных ЕГЭ по всем предметам

5 мая

Обновленный поиск заданий по ключевым словам

1 мая

Новый сервис: можно исправить ошибки!

29 апреля

Разместили актуальные шкалы ЕГЭ  — 2023

24 апреля

Учителю: обновленный классный журнал

7 апреля

Новый сервис: ссылка, чтобы записаться к учителю

30 марта

Решения досрочных ЕГЭ по математике

31 октября

Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР

НАШИ БОТЫ

Все новости

ЧУЖОЕ НЕ БРАТЬ!

Экзамер из Таганрога

10 апреля

Предприниматель Щеголихин скопировал сайт Решу ЕГЭ

Наша группа

Каталог заданий.
Преобразования числовых логарифмических выражений

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 16 № 26844

Найдите значение выражения

Аналоги к заданию № 26844: 26891 514738 514758 … Все

Решение

Помощь

Тип 16 № 26845

Найдите значение выражения

Аналоги к заданию № 26845: 68467 4329 4331 … Все

Решение

Помощь

Тип 16 № 26846

Найдите значение выражения

Аналоги к заданию № 26846: 68509 68469 68471 … Все

Решение

Помощь

Тип 16 № 26847

Найдите значение выражения

Аналоги к заданию № 26847: 68553 68511 68513 … Все

Решение

Помощь

Тип 16 № 26848

Найдите значение выражения

Аналоги к заданию № 26848: 4433 506468 506591 … Все

Решение

Помощь

Пройти тестирование по этим заданиям

О проекте · Редакция · Правовая информация · О рекламе

Источник

Итоговый экзамен по математике сдают все. Те, кто поступает на гуманитарные специальности (филология, юриспруденция, международные отношения) выбирают базовый уровень — вопросы в нем легче, а оценки «3» достаточно для получения аттестата. Профильный уровень сдают будущие экономисты, инженеры и программисты — на этих специальностях без знания математики не обойтись, ее обязательно изучают на первых курсах. Но это непростой предмет. Даже в профильных математических классах не всегда дают достаточно знаний. Если ваша цель — поступление в топовый вуз на техническую специальность, без курсов подготовки к ЕГЭ не обойтись. Это касается не только профильного уровня, но и ЕГЭ по математике базового. «Задание 2, как решать?» — часто спрашивают школьники, сдающие этот экзамен. В этой статье мы проведем разбор задания 2 из ЕГЭ по математике профильного и базового уровня.

Теория

В задании 2 ЕГЭ по профильной математике теория достаточно простая. Это номер базового уровня сложности, он приносит 1 балл. Выпускникам дается график (иногда — диаграмма), нужно проанализировать его в соответствии с условием. Определение аргумента функции, поиск максимального и минимального значения — навыки, которые нужны для этого задания ЕГЭ. 2 часть математики профильного уровня тоже содержит номера с графиками, поэтому эта теория пригодится и там. То, что нужно знать для решения задания 2 ЕГЭ по математике профильного уровня:

функция и ее график;
оси абсцисс и ординат;
промежутки возрастания и убывания функции;
области определения и значения функции;
максимум и минимум функции;
наибольшее и наименьшее значения на промежутке;
диаграммы;
цена деления на графике.

Перечисленные понятия нужны для сдачи любого уровня ЕГЭ. Но задание 2 по базовой математике проверяет другие навыки. В нем выпускник должен произвести вычисления со степенями. Этот номер тоже считается легким, однако для его выполнения нужно знать куда больше теории. Формулы для ЕГЭ по базовой математике, к заданию 2:

определение степени — an = a • a • a … • a, где n — натуральное число. a называют основанием степени, n — показателем.
a0 = 1.
a1 = a.
a-n = 1 / an.
anm=man.
an • am = an+m.
an • bn = (a • b)n.
an / am = an-m.
an / bn = (a / b)n.

Разбор задания 2

Решение задания 2 по математике ЕГЭ мы начнем с профильного уровня.

Задача. Замеры температуры проводились в течение 3 дней. Какой была минимальная температура 18 апреля?

Решение. Подобное задание 2 на ЕГЭ по математике профильного уровня кажется очень простым, однако в нем легко ошибиться. Обратим внимание на два момента: «18 апреля» и «минимальная». Для начала отсекаем колонки, относящиеся к 19 и 20 апреля — про них ничего не спрашивают. После этого ищем самую низкую точку и находим ее ординату.

Ответ: 6.

Задача. В помещении стоит кондиционер с датчиком температуры. Когда она достигает определенного максимального значения, кондиционер включается. Когда комната остужается до необходимой температуры, кондиционер автоматически выключается. На графике показана зависимость температуры от времени. Укажите, сколько минут кондиционер был выключен.

Решение. В этом номере важно умение логически рассуждать. Когда кондиционер отключен, температура увеличивается. На графике это показывается ростом функции вверх. Чтобы определить, сколько минут кондиционер был выключен, нужно найти область возрастания функции. Это промежуток между числами 6 и 9 на оси абсцисс. Теперь мы ищем время: 9 — 6 = 3.

Ответ: 3.

За выполнение такого простого номера можно получить 1 балл на экзамене по математике. Разбор задания 2 ЕГЭ мы продолжим базовым уровнем. Здесь встречаются несколько типов вопросов: степенные выражения с одинаковыми и разными основаниями, поиск частного, произведения и суммы. Чтобы посмотреть все существующие виды заданий, зайдите на «Решу ЕГЭ» по базовой математике. Задание 2 там представлено более чем 40 вариантами. А в рамках этой статьи мы разберем несколько примеров задания 2 из ЕГЭ по математике базового уровня.

Найти значение выражения

Задача. 4 • 72 + 6 • 72.

Решение. У слагаемых есть общий множитель, который мы можем вынести за скобку. После этого считаем выражение в скобке, потом возводим число в степень и перемножаем: (4 + 6) • 72 = 10 • 72 = 10 • 49 = 490.

Ответ: 490.

Найти значение выражения (разные основания)

Задача. 8^0,76 • 64^0,12.

Решение. Нужно привести степени к одинаковому основанию, представив 64 как 82. После этого их можно перемножить: 8^0,76 • 64^0,12 = 8^0,76 • (8)^2*0,12 = 8^0,76+0,24 = 8¹ = 8.

Ответ: 8.

Найти значение выражения (одинаковые основания)

Задача. 26 • 2-2 / 22.

Решение. В данном примере расчеты можно провести сразу же. Умножение степеней с одинаковым основанием заменяем на сложение показателей, деление — на их вычитание: 26 + (-2) — 2 = 26 — 4 = 22 = 4.

Ответ: 4.

Найти частное от деления

Задача. 1,6 • 102 : 4 • 10-2.

Решение. У степеней одинаковое основание, поэтому мы можем поделить их, найдя разность показателей. После этого мы делим числа без степеней и выполняем умножение: 1,6 : 4 • 102 — (-2) = 1,6 : 4 • 104 = 1,6 : 4 • 10000 = 0,4 • 10000 = 4000.

Ответ: 4000.

Найти произведение

Задача. 4 • 105 • 2,3 • 10-7.

Решение: Степени имеют одинаковые основания, поэтому мы можем умножить их, сложив показатели. После этого результат умножаем на остальные числа: 4 • 2,3 • 105 + (-7) = 4 • 2,3 • 10-2 = 4 • 2,3 • 0,01 = 9,2 • 0,01 = 0,092.

Ответ: 0,092.

Найти сумму

Задача. 9,4 • 102 + 2,1 • 103.

Решение. Мы возводим числа в степень, затем выполняем умножение и сложение: 9,4 • 100 + 2,1 • 1000 = 940 + 2100 = 3040.

Ответ: 3040.

Теперь вы знаете чуть больше теории для ЕГЭ по математике. Задание 2 из профильного уровня достаточно легкое (хотя без практики тут тоже не обойтись), а вот в базе придется рассуждать и выполнять вычисления. Но и его можно выполнить без труда, если должным образом подготовиться к ЕГЭ. Однако, лучший результат всегда дают занятия с опытными преподавателями, знающими специфику экзамена. Если нанимать репетитора для вас дорого, обратите внимание на курсы. Там разбирают не только задание 2 ЕГЭ по математике, но и многие другие номера, в том числе вторую часть. Грамотная подготовка — ключ к хорошим баллам, а значит, и месту на бюджете.

Источник

Значение выражений

[su_box title=”Описание задания” style=”soft” box_color=”#c1e8cc” title_color=”#0c0a0a”]

В задании №5 ЕГЭ по математике базового уровня нам необходимо вычислить значение выражения, пользуясь различными правилами: формулами сокращенного умножения, знаниями тригонометрии, свойствами логарифмов и другими. Данное задание требует более глубоких знаний и значительно сложнее первого задания, где достаточно было знать элементарные математические операции.

Тематика заданий: значение выражений

Бал: 1 из 20

Сложность задания: ♦♦♦

Примерное время выполнения: 5-7 мин.

[/su_box]

Теория к заданию №5

В данном задании, кроме операций со степенями, о которых мы говорили в прошлых заданиях, необходимо помнить формулы сокращенного умножения:

Кроме этого, очень часто встречаются задания на знания свойств логарифма:

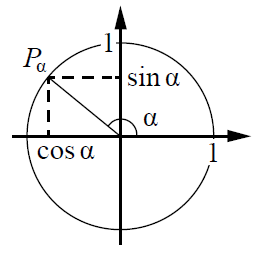
Полезными будут представления о тригонометрической окружности, по которой можно определять знаки тригонометрических функций:

Разбор типовых вариантов заданий №5 ЕГЭ по математике базового уровня

Во всех заданиях необходимо найти значение выражения.

Вариант 5МБ1

Алгоритм выполнения

Представим угол 390° с учетом периодичности функции tg меньшим углом.
Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
Выполним умножение.

Решение:

Функция tg является периодической с периодом 180°, то есть каждый раз при увеличении или уменьшении угла на 180° значение tg повторяется.

То есть tg α = tg (α + 180°) = tg (α – 180°)

tg 390° = tg (390° – 180°) = tg 210° = tg (210° – 180°) = tg 30°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 30° = √3/3

Подставим найденное значение в данное выражение.

20 · √3 · (√3/3) = (20 · √3 · √3)/3 = (20 · 3)/3 = 20

Решение в общем виде

Вычислим выражение, учитывая, что функция тангенс периодическая с периодом π радиан или 180°. Следовательно, угол 390° эквивалентен углу

и получаем выражение:

Ответ: 20.

Вариант 5МБ2

Алгоритм выполнения

Представим угол 420° с учетом периодичности функции tg меньшим углом.
Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.
Выполним умножение.

Решение №1:

То есть

tg α = tg (α + 180°) = tg (α – 180°)

tg 390° = tg (420° – 180°) = tg 240° tg (240° – 180°) = tg 60°

Найдем таблице значений тригонометрических функций (в справочных материалах) значение tg полученного угла.

tg 60° = √3

Подставим найденное значение в данное выражение.

-50 · √3 · √3 = -50 · 3 = -150

Решение №2:

Заметим, что функция тангенс периодическая с периодом π радиан или 180°. Поэтому, тангенс угла 420° эквивалентен тангенсу угла в

получаем:

Ответ: -150.

Вариант 5МБ3

Алгоритм выполнения

Объединим подкоренные выражения под один корень.
Внесем под корень дробь.
Сократим дробь под корнем.
Представим произведение под корнем в виде произведения вторых степеней.
Вынесем из под корня множители.
Выполним умножение.

Решение:

Объединим подкоренные выражения под один корень. Имеем право так сделать использовав, свойство квадратного корня.

5/3 · √27 · √3 = 5/3 · √(27 · 3)

Внесем под корень дробь.

Корень квадратный, следовательно, чтобы внести дробь под знак корня нужно возвести ее в квадрат. То есть умножить сам на себя числитель и знаменатель.

(5/3)² = (5 · 5)/(3 · 3)

Сократим дробь под корнем на три дважды.

Представим произведение под корнем в виде произведения вторых степеней.

Вынесем из под корня множители и выполним умножение.

Решение в общем виде:

Ответ: 15.

Вариант 5МБ4

[su_note note_color=”#defae6″]

Найдите cos α, если sin α = 0,8 и 90° ‹ α ‹ 180°.

[/su_note]

Алгоритм выполнения

Запишем основное тригонометрическое тождество.
Подставим в основное тригонометрическое тождество все известные данные.
Решим полученное уравнение относительно cos α.
Выбрать корни, подходящие к условию задания.

Решение:

Запишем основное тригонометрическое тождество.

sin² α + cos² α = 1

Подставим в основное тригонометрическое тождество все известные данные.

0,8² + cos² α = 1

Решим полученное уравнение относительно cos α.

cos² α – неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.

cos² α = 1 – 0,8²

Чтобы найти вторую степень числа нужно число умножить само на себя.

0,8² = 0,8 · 0,8 = 0,64

cos² α = 1 – 0,8² 1 – 0,64 = 0,36

cos α = √0,36

cos α = 0,6 или -0,6

Условие 90° ‹ α ‹ 180° означает, что -1 ‹ соs α ‹ 0.

Следовательно данному условию удовлетворяет только один корень -0,6.

Ответ: -0,6.

Вариант 5МБ5

[su_note note_color=”#defae6″]

(2√13 −1)(2√13 +1).

[/su_note]

Алгоритм выполнения

В данном задании необходимо сразу заметить формулу сокращенного умножения – разность квадратов (последняя формула сокращенного умножения в теории выше).

Решение:

После этого, решение задания сводится к следующему:

(2√13 −1)(2√13 +1) = (2√13)² – 1² = 4 • 13 – 1 = 51

Ответ: 51.

Вариант 5МБ6

[su_note note_color=”#defae6″]

5^log₅6+1 .

[/su_note]

Алгоритм выполнения

Сначала вспомним свойства степеней и разложим выражение следующим образом:

5^log₅6 • 5¹

Затем вспомним определение и свойство логарифма – это вторая строчка из нашей теории:

Решение:

Получим:

6•5 = 30

Ответ: 30

Вариант 5МБ7

[su_note note_color=”#defae6″]

(√11-√3)(√11+√3)

[/su_note]

Алгоритм выполнения

Применяем формулу сокращенного умножения a²–b²=(a-b)(a+b).
Используем определение кв.корня: (√a)²=a.
Находим полученную разность целых чисел.

Решение:

Исходя из алгоритма, подставляем а=√11, а b=√3, тогда 11-3=8

Ответ: 8

Вариант 5МБ8

Алгоритм выполнения

Применяем тождество log_a(xy)=log_ax+log_ay.
Преобразовываем множители, стоящие под знаком логарифма, в степени.
Используем для выражения под знаком логарифма св-во степеней a^xb^x=(ab)^x.
Используем св-во логарифмов xlog_ab=log_ab^x.
Применяем тождество log_aa=1,.

Решение:

log₆27 + log₆8 = log₆27·8 = log₆3³·2³ = log₆(3·2)³ = log₆6³ = 3log₆6 = 3

Ответ:3

Вариант 5МБ9

Алгоритм выполнения

Вносим множитель √6 в скобки.
Выполняем умножение √24 и √6. Получим √144. Это число является полным квадратом: (√12)².
Перемножаем √6 и √6. Получаем (√6)².
Используя определение кв.корня (√а)²=а, находим, что (√12)²=12, а (√6)²=6.
Находим разность полученных целых чисел.

Решение:

Ответ: 6

Вариант 5МБ10

Найдите sinα, если

Алгоритм выполнения

Применим основное тригонометрическое тождество. В тождество подставим данное в условии числовое значение для косинуса.
Выполняем преобразование тождества, получаем числовой результат.
Определяем знак результата, исходя из величины угла α.

Решение:

Ответ: 0,4

Вариант 5МБ11

Алгоритм выполнения

Выполняем 1-ю по приоритетности операцию – возведение в степень (в знаменателе). Для этого используем св-во степеней (ab)²=a²·b². Далее для множителя (√13)² применяем формулу, определяющую понятие кв.корня: (√а)²=а.
Выполняем умножение в знаменателе.
Представляем число 39 в числителе как произведение 3·13.
Сокращаем дробь на 13.
Переводим полученную обыкновенную дробь в десятичную.

Решение:

Ответ: 0,75

Вариант 5МБ12

Алгоритм выполнения

Применяем к показателю степени 2log₃7 св-во логарифмов log_b^ya^x=(x/y)log_ba. Получим log₃7².
Применяем св-во логарифмов a^log_a^b=b. В результате знак логарифма исчезает, остается только выражение 7², которое было под знаком логарифма.
Возводим 7 в квадрат.

Решение:

2log₃7 log₃7²

3 = 3 = 7² = 49

Ответ:49

Вариант 5МБ13

Алгоритм выполнения

Используем св-во корней √(a·b)=√a·√b. Таким способом √63 разложим на множители √9 и √7.
Сгруппируем одинаковые множители √7. Получим (√7)².
Основываясь на определении кв.корня (√а)²=а, представляем √9=(√3)².
Возводим полученные числа в квадрат.
Находим итоговое произведение.

Решение:

Ответ: 21

Вариант 5МБ14

Алгоритм выполнения

Используем св-во степеней x^a+b=x^a·x^b. Получим 2 множителя, первый из которых равен 7, а второй представляет собой степень с основанием 7 и показателем, содержащим логарифм.
Для второго множителя применим св-во логарифмов a^loga^b=b.
Находим результирующее произведение.

Решение:

Ответ: 21

Вариант 5МБ15

Алгоритм выполнения

Для cos 390⁰ используем ф-лу приведения cos (360⁰+α)=cos α. Получим cos 30⁰=√3/2. Записываем получившееся выражение в виде дроби со знаменателем 2.
Вычисляем произведение √3·√3 путем возведения в степень. Для этого используем определение кв.корня: (√а)²=а.
Сокращаем 20 в числителе и 2 в знаменателе на 2.
Находим конечное произведение.

Решение:

Ответ: 30

Вариант 5МБ16

Алгоритм выполнения

Преобразовываем часть выражения, взятую в скобки. Для этого представляем 49 как 7². Затем используем св-во логарифмов log_ba^x=xlog_ba, а далее св-во log_aa=1. Получаем 2.
Применяем св-во логарифмов log_aa=1.

Решение:

log₂(log₇49) = log₂(log₇7²) = log₂(2log₇7) = log₂2 = 1

Ответ: 1

Даниил Романович | Просмотров: 14k

Источник

Теория

Разбор задания 2

Найти значение выражения (разные основания)

Найти значение выражения (одинаковые основания)

Найти произведение

Найти сумму

Значение выражений

Теория к заданию №5

Разбор типовых вариантов заданий №5 ЕГЭ по математике базового уровня

Вариант 5МБ1

Алгоритм выполнения

Решение:

Решение в общем виде

Вариант 5МБ2

Алгоритм выполнения

Решение №1:

Решение №2:

Вариант 5МБ3

Алгоритм выполнения

Решение:

Вариант 5МБ4

Алгоритм выполнения

Решение:

Вариант 5МБ5

Алгоритм выполнения

Решение:

Вариант 5МБ6

Алгоритм выполнения

Решение:

Вариант 5МБ7

Алгоритм выполнения

Решение:

Вариант 5МБ8

Алгоритм выполнения

Решение:

Вариант 5МБ9

Алгоритм выполнения

Решение:

Вариант 5МБ10

Алгоритм выполнения

Решение:<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://spadilo.ru/wp-content/uploads/2019/01/c-users-ksenya-desktop-korin-png-e1560417170386.png" alt width="483" height="62" />

Вариант 5МБ11

Алгоритм выполнения

Решение:<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://spadilo.ru/wp-content/uploads/2019/01/c-users-ksenya-desktop-55-png-e1560417394213.png" alt width="238" height="59" />

Вариант 5МБ12

Алгоритм выполнения

Решение:

Вариант 5МБ13

Алгоритм выполнения

Решение:<img decoding="async" onError="javascript: wp_broken_images = window.wp_broken_images || function(){}; wp_broken_images(this);" loading="lazy" src="https://spadilo.ru/wp-content/uploads/2019/01/c-users-ksenya-desktop-k33-png-e1560417526909.png" alt width="221" height="28" />

Вариант 5МБ14

Алгоритм выполнения

Решение:

Вариант 5МБ15

Алгоритм выполнения

Решение:

Вариант 5МБ16

Алгоритм выполнения

Решение:

Не пропустите также:

Решение:

Решение:

Решение: