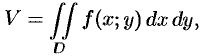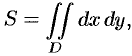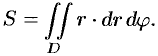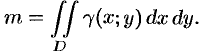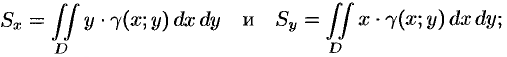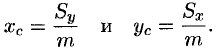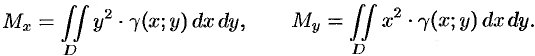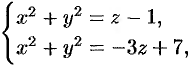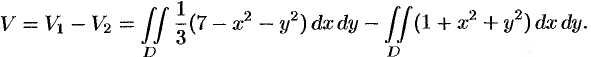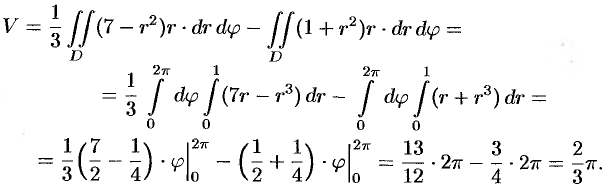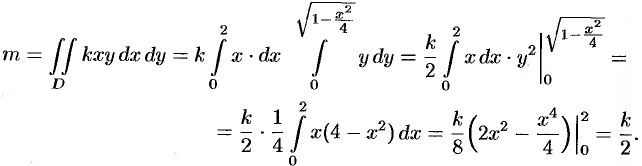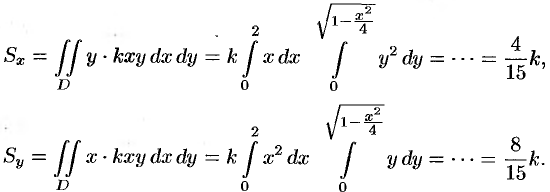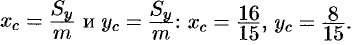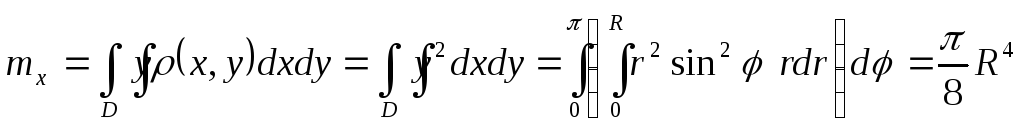Приложения двойного интеграла
Приведем некоторые примеры применения двойного интеграла.
Объем тела
Как уже показано (п. 53.2), объем цилиндрического тела находится по формуле
где 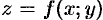
Площадь плоской фигуры
Если положить в формуле (53.4) 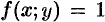
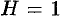




или, в полярных координатах,
Масса плоской фигуры
Как уже показано (п. 53.2), масса плоской пластинки 
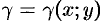
Статические моменты и координаты центра тяжести плоской фигуры
Статические моменты фигуры 

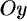
а координаты центра масс фигуры — по формулам
Моменты инерции плоской фигуры
Моментом инерции материальной точки массы 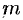
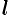
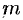
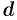
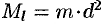

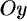
Момент инерции фигуры относительно начала координат — по формуле 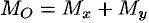
Замечание. Приведенными примерами не исчерпывается применение двойного интеграла. Далее мы встретим приложение двойного интеграла к вычислению площадей поверхностей фигур (п. 57.3).
Пример №53.3.
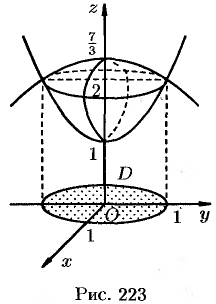
Найти объем тела, ограниченного поверхностями 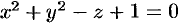
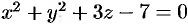
Решение:
Данное тело ограничено двумя параболоидами (см. рис. 223). Решая систему
находим уравнение линии их пересечения: 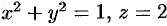
Искомый объем равен разности объемов двух цилиндрических тел с одним основанием (круг 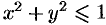
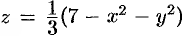
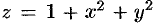
Переходя к полярным координатам, находим:
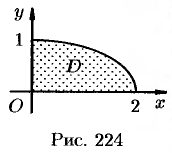
Пример №53.4.
Найти массу, статические моменты 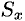
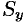
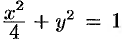
Решение:
По формуле (53.6) находим массу пластинки. По условию, 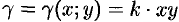
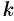
Находим статические моменты пластинки:
Находим координаты центра тяжести пластинки, используя формулы
На этой странице размещён полный курс лекций с примерами решения по всем разделам высшей математики:
- Решение задач по высшей математике
Другие темы по высшей математике возможно вам они будут полезны:
Приложения двойного интеграла.
С помощью
двойного интеграла можно вычислить
объем цилиндрического тела, площадь и
массу плоской области. От этих задач мы
и пришли к двойному интегралу.
Но возможны и
менее очевидные приложения.
С помощью
двойного интеграла можно вычислять
площадь поверхности, определять
статические моменты, моменты инерции
и центр тяжести плоской области.
Вычисление площади поверхности с помощью двойного интеграла.
|
|
Пусть поверхность , Введем разбиение на ячейкиk, |
то можно считать
справедливым соотношение vkcosk=sk.
Выразим отсюда
vk=sk/cosk.
Будем измельчать разбиение при условииmaxdiamk0, что
для кусочно-гладкой поверхности, не
ортогональной плоскостиOXY,
равносильноmaxdiamdk0.
Вычислим площадь поверхности как
двойной интеграл
.
Сюда остается
лишь подставить
.
Если
поверхность задана
уравнениемF(x,y,z) = 0, то
Поэтому в этом
случае



Если поверхность
задана уравнением z=f(x,y), то уравнение это можно
свести к уравнению
F(x,y,z) = 0 и применить выведенную
формулу:
.
Пример.Вычислить площадь поверхности конуса,
ограниченной плоскостями
|
|
|
Вычисление статических моментов, координат центра тяжести, моментов инерции.
Пусть задана
плотность вещества плоской материальной
области D(x,y). Выделим элементарную
ячейку с массойdmи применим
к ней известные формулы для материальной
точки:
Статические
моменты относительно осей OX,OYdmx
=ydm=y(x,y) ds,
dmy
= x dm = x (x,
y) ds.
Моменты инерции
относительно осей OX,OYdJx=y2dm=y2(x,y) ds,
dJy
= x2
dm = x2
(x,
y) ds.
Момент инерции
относительно начала координат dJ0=dJx+dJy.
Двойным интегралом по всей
области Dвычисляем те же
характеристики для областиD.
,
,
,
,J0=Jx
+Jy.
Координаты центра тяжести
,
где
— масса областиD.
Пример.Вычислить координаты
центра тяжести полукругас заданной плотностью
.
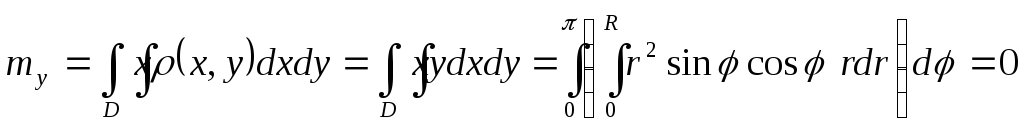
полукруга относительноOYи
независимости плотности от координатыx).
Поэтому
.
Пример.Вычислить момент инерции полукруга
с заданной плотностью
относительно прямой
.
.
Эта формула
известна в теоретической механике.
Замечание о несобственных двойных интегралах.
Точно так же,
как и в определенных интегралах, вводят
несобственные двойные интегралы двух
типов: интеграл от непрерывной функции
по неограниченной области (первого
рода) иинтеграл от разрывной функции
по ограниченной области (второго
рода).
Интеграл первого
рода определяют как предел последовательности
двойных интегралов от непрерывной
функции по «расширяющимся» областям,
стремящимся к заданной неограниченной
области. Если предел существует и
конечен, то интеграл называется
сходящимся, если предел не существует
или бесконечен, то интеграл называется
расходящимся.
Интеграл второго
рода6определяют как предел последовательности
интегралов от непрерывной функции по
«расширяющимся» областям, стремящимся
к заданной области и исключающим точку
разрыва. Если предел существует и
конечен, то интеграл называется
сходящимся, если предел не существует
или бесконечен, то интеграл называется
расходящимся.
Пример.Показать, что несобственный интеграл
первого рода
по области
сходится при
и расходится при
.
Показать, что
несобственный интеграл первого рода
по области
сходится при
и расходится при
.Вычислим
этот интеграл по области
.

=
=
Часто расширение математических
знаний позволяет решать задачи, которые
не получались старыми методами.
Пример.Вычислить интеграл Пуассона
.
Неопределенный
интеграл
«не берется». Но двойной интеграл по
области
равен
I=.
С другой стороны,
переходя к полярным координатам, получим
I =
.
Поэтому
=
.
По четности
.
(схема 42)
1. Вычисление объема тела
Пусть функция f(x;y) ≥ 0.
Рассмотрим тело, ограниченное
поверхностью z = f(x;y), плоскостью z=0 и цилиндрической поверхностью, образующие которой
параллельны оси 0z, а направляющей
служит граница области D. Как было показано
выше, согласно формуле (6.3) объем данного тела равен

Пример 6.9. Вычислить объём тела, ограниченного параболоидом z= x2+y2+1,
плоскостью x+y
–3=0 и координатными плоскостями.
Решение. Основанием тела служит треугольник ОАВ. Область D в данном
случае определяется неравенствами:

изображенному на рисунке 6.6 (пример 6.5). Следовательно, используя формулу
(6.18), получим:
2.
Вычисление площади плоской фигуры
Если положить в формуле (6.18) f(x,y)=1, то цилиндрическое тело «превратится» в прямой цилиндр с высотой h=1. Объем такого цилиндра,
как
известно, численно равен площади S основания D. Получаем формулу для вычисления площади S области D:

или, в полярных
координатах,

Пример
6.10. Вычислить площадь фигуры,
ограниченной прямой y=2x+1 и параболой y=x2+1.
Решение. Решая совместно систему

и B(2;5).
Применяя формулу (6.19), будем иметь:
Пример 6.11. Вычислить площадь фигуры ограниченной лемнискатой

Решение. Переходим к полярной системе координат, полагая x=r cosφ и y=r sinφ; тогда получаем

можно вычислить сначала ту часть, которая расположена первой четверти. В этом случае угол φ будет изменяться от 0 до

3.
Вычисление массы плоской фигуры (пластины)
Масса плоской пластинки D с
переменной плотностью γ=γ(x,y) находится
по формуле

4.
Определение статических моментов и координат центра тяжести плоской фигуры
Статические моменты фигуры D относительно осей 0x и 0y могут быть вычислены по формулам

а
координаты центра масс фигуры – по формулам

Статические моменты широко используются в
сопротивлении материалов и других технических науках.
5.
Определение моментов инерции плоской
фигуры
Моментом инерции материальной точки массы m относительно оси l называется произведение массы m на
квадрат расстояния d точки до оси, т.е. 
вычислены по формулам:

Момент
инерции фигуры относительно начала координат – по формуле

Пример
6.12. Найти массу, статические
моменты и координаты центра тяжести фигуры, лежащей в первой четверти,
ограниченной эллипсом 
Поверхностная плотность в каждой точке фигуры пропорциональна произведению
координат точки.
Решение. По
формуле (6.21) находим массу пластины. По условию, γ=γ(x,y)=k∙xy, где k –
коэффициент пропорциональности.Тогда

Находим
статические моменты пластинки по формулам (6.22):
Находим
координаты центра тяжести пластинки, используя формулы (6.23):
6. Поверхностный интеграл I рода
Обобщением двойного интеграла является поверхностный интеграл. Пусть в трехмерном пространстве Оxyz в точках некоторой поверхности площади S определена непрерывная функция u = f (x;y;z). Разобьем поверхность на конечное число n частей Si, площади которых равны ∆Si, а диаметры – di, 
и составим сумму произведений вида

Она
называется интегральной суммой для функции f(x;y;z) по поверхности S. Если при 
сумма (6.26) имеет предел, который не зависит ни от способа разбиения поверхности S, ни от выбора точек Mi(xi;yi;zi), то он называется поверхностным интегралом I рода от
функции f(x;y;z) по поверхности S и обозначается 

Теорема 6.3
(о существовании поверхностного интеграла). Если поверхность S гладкая (в каждой ее точке существует касательная
плоскость, которая непрерывно меняется с перемещением точки по поверхности), а
функция f(x;y;z) непрерывна на этой поверхности, то поверхностный
интеграл существует
Формула 
выражает интеграл по поверхности
S
через двойной интеграл по проекции S на плоскость x0y. Отметим, что если поверхность S задана
уравнением вида y=y(x;z) или x=x(y;z), то аналогично получим:


где
D1 и D2 –
проекции поверхности S на
координатные плоскости xОz и yОz
соответственно.
Пример 6.13. Вычислить 

Решение. Из уравнения заданной
цилиндрической поверхности выразим 
при x = 0 в плоскости xОy: 

имеем
Приведем некоторые примеры применения
поверхностного интеграла I рода.
6.1. Площадь
поверхности
Если поверхность S задана уравнением z = f(x;y), a ее проекция на
плоскость x0y есть область D, в которой z = f(x;y), zx(x;y) и zy(x;y) –
непрерывные функции, то ее площадь S
вычисляется по формуле:

Пример 6.14. Вычислить площадь части плоскости x+y+z=4,
вырезаемой цилиндром x2+y2 =4 (рис. 6.10).
Решение. Применим формулу (6.31). Область интегрирования D есть круг
радиуса r=2. Находим частные производные

функции z=4 – x – y:


Чтобы вычислить этот интеграл, введём полярные
координаты. Область D определяется: 
Кроме того, поверхностный интеграл применяют для
вычисления массы, координат центра масс, моментов инерции материальных
поверхностей с известной поверхностной плотностью распределения массы γ=γ(x;y;z). Все эти величины
определяются одним и тем же способом:
– данную область разбивают на конечное число мелких частей;
– делают для каждой такой части предположения, упрощающие задачу;
– находят приближенное значение искомой величины;
– переходят к пределу при неограниченном измельчении разбиения
области.
Проиллюстрируем описанный способ на примере
определения массы материальной поверхности.
6.2. Масса
поверхности
Пусть плотность распределения массы материальной
поверхности есть γ=γ(x;y;z). Для нахождения
массы поверхности:
1. Разбиваем поверхность S на n частей Si, 
2. Выберем произвольную точку Mi(xi;yi;zi) в каждой области Si. Предполагаем, что
в переделах области Si
плотность постоянна и равна её
значению в
точке Mi.
3. Масса mi области Si мало отличается от
массы γ(xi;yi;zi)∙∆Si однородной области с постоянной полностью γ= γ(xi;yi;zi).
4. Суммируя mi
по всей области, получаем:
5. За точное значение массы материальной поверхности S
принимается предел, к которому стремится полученное приближенное значение при
стремлении к нулю диаметров областей Si, то есть

6.3. Моменты
и центр тяжести поверхности. Статические
моменты, координаты центра тяжести, моменты инерции материальной поверхности S находятся по
соответствующим формулам:
Пример 6.15.
Вычислить координаты центра тяжести
однородной поверхности параболоида z=x2+y2, ограниченной плоскостью z=1.
Решение. Вершина заданного параболоида совпадает с началом
координат. Так как поверхность однородная (постоянная плотность массы), то,
основываясь на ее симметрии, можно сделать вывод, что центр тяжести расположен
на оси 0z. Тогда xc=0, yc=0
и по формуле (6.36) аппликата
спроектируем линию пересечения на плоскость x0y – получим окружность x2+y2=1 в
качестве области D. Вычислим элемент поверхности параболоида z=x2+y2 по
формуле (6.31), учитывая, что

Аналогично, переходя к полярным координатам на
плоскости x0y, получим:

Таким образом,
пересечения поверхности с плоскостью
Приложения кратных интегралов в механике
Краткая теория
Масса и статистические моменты пластики
Если
– область плоскости
, занятая пластинкой, и
– поверхностная плотность пластики в точке
, то масса
пластинки и ее статистические моменты
и
относительно осей
и
выражаются двойными интегралами:
Если
пластика однородна, то
Координаты центра тяжести пластики
Если
– центр тяжести пластики, то
где
– масса пластинки и
– ее статистические моменты относительно осей
координат.
Моменты инерции пластики
Моменты
инерции пластинки относительно осей
и
соответственно равны:
Момент инерции пластики относительно
начала координат:
Полагая
, получаем геометрические моменты инерции плоской
фигуры.
Масса тела, занимающего область
![]() и статистические моменты тела относительно
и статистические моменты тела относительно
координатных плоскостей
где
– плоскость тела в точке
Координаты центра тяжести
Если тело
однородно, то формулах для координат центра тяжести можно положить
.
Моменты инерции относительно
осей координат
Полагая в
этих формулах
, получаем геометрические
моменты инерции тела.
Примеры решения задач
Задача 1
Вычислить
массу материальной пластины, занимающей область
плоскости
, если поверхностная
плотность
и границы области
заданы уравнениями.
Решение
Сделаем
чертеж области
:
Искомая
масса материальной пластины:
Ответ:
Задача 2
Найти
статистический момент фигуры, ограниченной линиями
и
относительно оси абсцисс.
Решение
Сделаем
чертеж:
Статистический
момент относительно оси
:
Ответ:
Задача 3
Вычислить
координаты центра масс однородной
материальной пластины
, ограниченной данными
линиями:
Решение
Сделаем
чертеж:
Масса
пластинки:
Статистические
моменты:
Искомые
координаты центра масс:
Ответ:
.
Задача 4
Вычислить массу тела
, ограниченного заданными поверхностями
-плотность в
точке
.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Изобразим
тело на рисунке:
С боков
тело будет ограничено цилиндром
и плоскостями
. Сверху плоскостью
Проекция на плоскость
:
Ответ:
Задача 5
Найти
момент инерции однородного шара
с массой
относительно оси
.
Решение
Момент
инерции относительно оси
можно найти по формуле:
Шар
однородный, поэтому плотность:
Перейдем
к сферическим координатам:
Получаем:
Ответ:
Содержание:
- Пример 3:
- Координаты центра тяжести
По этой ссылке вы найдёте полный курс лекций по математике:
Масса плоской фигуры Пусть задана плоская ограниченная фигура D, по которой непрерывным образом распределена масса с поверхностной плотностью — функция, непрерывная в D. Разобьем фигуру D на п частей без общих внутренних точек, площади которых соответственно равны В каждой части произвольно выберем точку У к) и вычислим в ней плотность у*).
В силу непрерывности fi(x, у) можно считать, что масса т* части Dk фигуры D приближенно равна а масса всей фигуры — сумме Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат Координаты центра тяжести Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей
Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области Последняя является интегральной суммой для непрерывной функции ц(х} у) в области D. Переходя к пределу при d 0 (здесь d — наибольший из диаметров частичных областей получим точное равенство Если масса распределена равномерно по всей фигуре, ц = const, то формула (1) принимает вид Пример 1.
Найти массу кольца, ограниченного двумя концентрическими окружностями радиусов г и Л, где если плотность кольца в каждой точке обратно пропорциональна расстоянию от этой точки до центра окружности и равна 1 на окружности внутреннего круга где S — площадь фигуры D.
М Фигура D задается условиями 9.2. Статические моменты плоской фигуры относительно осей координат. Координаты центра тяжести Статическим моментом Мх материальной точки массы т относительно оси Ох называется произведение ту, где у — ордината материальной точки, т. е. Здесь у может быть как положительным, так и отрицательным числом. Разбивая фигуру D на части , выбирая в каждой части Dk произвольно точку и считая, что масса этой к-й части приближенно равна и сосредоточена в точке , запишем приближенно величину статического момента фигуры D относительно оси Ох. Имеем где ASk — площадь части ) — поверхностная плотность.
Переходя к пределу при d -* 0, получаем Статический момент фигуры D относительно оси Оу находится по аналогичной формуле Если известны статические моменты Мх и Mv и масса т плоской фигуры, то координаты центра тяжести этой фигуры находятся по следующим формулам Если /1 = const, то m = /iS, где S — площадь фи гуры D, и формулы (5) принимают вид: Пример 2.
Найти центр тяжести однородн ой плоской фигуры, ограниченной косинусоидой Так как фигура — однородная, то координаты центра тяжести будем искать по фор мулам (6). Найдем сначала площадь S заданной фигуры. Имеем Затем найдем статические моменты Теперь no формулам (6) получаем Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат Координаты центра тяжести Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области 9.3.
Моменты инерции плоской фигуры относительно осей координат Рассуждая аналогично изложенному выше, легко установить, что элементарные моменты инерции относительно осей Ох и Оу будут соответственно равны Интегрируя по плоской фигуре £>, получим формулы для самих моментов инерции где, как и ранее, — поверхностная плотность распределения масс. 9.4. Вычислен ие массы тела Рассматривая задачу, приводящую к тройному интегралу, мы показали, что если известна плотность распределения масс fi(x} у, г) в каждой точке некоторого тела ft, то масса этого тела вычисляется по формуле Мы предполагаем, что функция у, z) непрерывна в области П.
Возможно вам будут полезны данные страницы:
Пример 3:
Вычислить массу m тела, ограниченного полусферами и плоскостью хОу, если плотность в каждой точке пропорциональна расстоянию от этой тон ни до начала координат. 4 По условию задачи плотаостъ ц в точке (x,y,z) выражается формулой — коэффициент пропорциональности. Тогда Переходя к сферическим координатам, получим, что 9.5. Статические моменты тела относительно координатных плосюствв .
Центр тяжести Напомним, что задача о вычислении статических моментов и центра тяже сти плоской фигуры решалась при помощидвойных интегралов (см. формулы (3), (4) и (5)). Задачи о вычислении статических моментов тела ft относительно координатных плоскостей и отыскания центра тяжести тела ft решаются аналогичным способом при помощи тройных интегралов. Например, элементарный статический момент относительно плоскости хОу равен — плотность. Отсюда статический момент Аналогично выписываются статические моменты относительно плоскостей Вычислив массу m тела ft и его статические моменты, легко найти координаты центра тяжести тела:
Если тело однородно, то плотность = const и формулы (11) упрощаются — постоянный множитель /х в числителе можно вынести за знак интеграла и сократить на него числитель и знаменатель . Тогда получим 4. найти координаты центра тяжести Однородное о полуиира радиуса R. 4 Считаем, что центр шара находится в начале координат, а рассматриваемая фигура — полуша р расположена над плоскостью. Тогда в силу симметрии имеем Объем полушара равен Найдем статический момент относительно плосхости хОу: Значит, центр тяжести.
Понятие о несобственном кратном
интеграле по неограниченной области При необходимости интегрирования функций нескольких переменных по неограниченной области D поступают так. Выбирают последовательность ограниченных областей интегрирования , монотонно исчерпывающих область D, т. е. Например, если область интегрирования {Д,} совпадает со всей плоскостью , то за последовательность {Dn} можно принять совокупность концентрических кругов где Определение. Несобственным интегралом от функции /(ж, у) по неограниченной области интегрирования D называется предел последовательности интегралов не зависящий от выбора последовательности D„.
Итак, по определению (2) Если предел (1) существует и конечен, то несобственный интеграл по неограниченной области называется сходящимся, в противном случае — расходящимся. Пример 1. Вычислить интеграл где область интегрирования — вся плоскость. м В качестве областей интегрирования {Dn} выберем круги радиуса п . Переходя к полярным координатам, получим Итак, интеграл (3) сходится и равен Признак сражение.
Если ,u интеграл сходится, то сходится и интеграл Если же интеграл расходится, то расходится и интеграл Интегралы, сходящиеся на всей плоскости, можно вычислять с помощью повторного интегрирования: 2. Вычислить интеграл 4 Так как то, согласно соотношению Переходя в двойном интеграле к полярным координатам, получим ноаую область интегрирования Следовательно, откуда Несобственные интегралы от функции трех, четырех и большего числа переменных по неограниченным областям определяются аналогично. Упражнения Вычислите двойные интегралы:
Измените порядок интегрирования (предварительно нарисовав область интегрирования): Нарисуйте область интегрирования и вычислите повторные интегралы Вычислите площади фигур, ограниченных кривыми Вычислите площадь петли кривой Вычислите площадь петли кривой Указание. Сделайте замену переменных Пугем перехода к полярным координатам вычислите следующие интегралы: если область D ограничена окружностью с центром в начале координат. — кольцо между окружностями радиусов полукруг диаметра d с центром в точке С о) , лежащий выше Приложения двойных и тройных интегралов Масса плоской фигуры Статические моменты плоской фигуры относительно осей координат
Координаты центра тяжести
Моменты инерции плоской фигуры относительно осей координат Статические моменты тела относительно координатных плоскостей Центр тяжести Понятие о несобственном кратном интеграле по неограниченной области Найдите массу штастиики D с заданной поверхностной плотностью Определите центры тяжести: 31. Полусегмента параболы 32. Полуэллипса отсеченного осью Ох. 33. Фигуры, ограниченной кривыми Вычислите площадь: 34.
Той части плоскости , которая лежит в первом октанте и ограничена цилиндром 35. Той части поверхности конусах которая высекается цилиндром 36. Поверхности параболоида расположенного внутри цилиндра . Вычислите интегралы по площади поверхности: 3часть плоскости , лежащая в первом октанте. где ж — часть сферы лежащая в первом октанте. — цилиндр х ограниченный плоскостями расстояние от точки ) поверхности до начала координат. Определение. Моментом инерции плоской фигуры относительно начала координат называется величина ‘ Вычислите моменты инерции относительно начала координат: 40.
Треугольника, ограниченного линиями , относительно оси Ох. 41. Треугольника с вершинами в точках относительно оси Оу. 42. Эллипса относительно оси Оу. 43. Области, ограниченной параболой у2 = 4ах, прямой Вычислите тройные интегралы: — область, ограниченная координатными плоскостями и плоскостью где ft — область, ограниченная конусом и плоско- — трехгранная призма, ограниченная плоскостя- п ми Вычислите инте1ралы 47-50, переходя к цилиндрическим или сферическим координатам: I
Вычислите объем тела, огранич енного данными поверхностями: . Указание: перейдюе к сферическим координатам. Вычислите массу тела: 54. Ограниченного поверхностями , «ели плогность ц в каждой точке тела равна аппликате этой точке. 55. Ограниченного поверхностями , если плотность/х в каждой точке равна орданате у этой точки.
Найдете статические моменты однородного тела (ц = 1): 56. Прямоугольного параллелепипеда с ребра*» а, Ь,с, относительно его граней. 57. Тела, ограниченного эллипсоидом х2 у2 z2 и плоскостью хОу, относительно плоскости хОу. Найдите координаты центра тяжести однородного тела (/* = 1), ограниченного данными поверхностями: 58. Плоскостями 59. Цилиндром и плоскостями 60. Параболоидом х2 + у2 = 2л z и полусферой .
Лекции:
- Производная функции
- Найдите наименьшее значение функции на отрезке
- Собственные числа матрицы
- Системы линейных дифференциальных уравнений
- Свойства пределов функции
- Таблица производных полная: для студентов
- Функции двух переменных. Действия над случайными величинами
- Найти значение выражения
- Исследование графика функции
- Существование предела