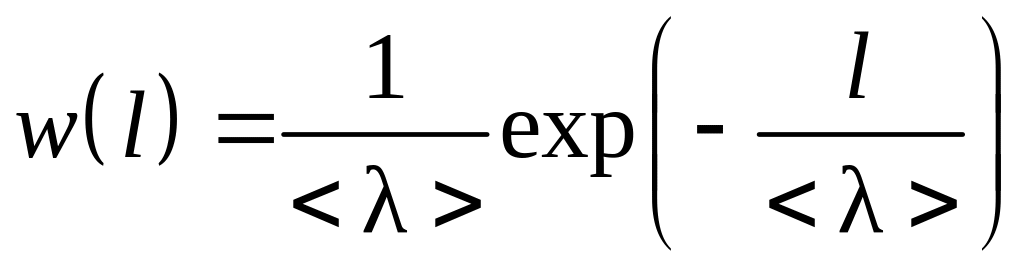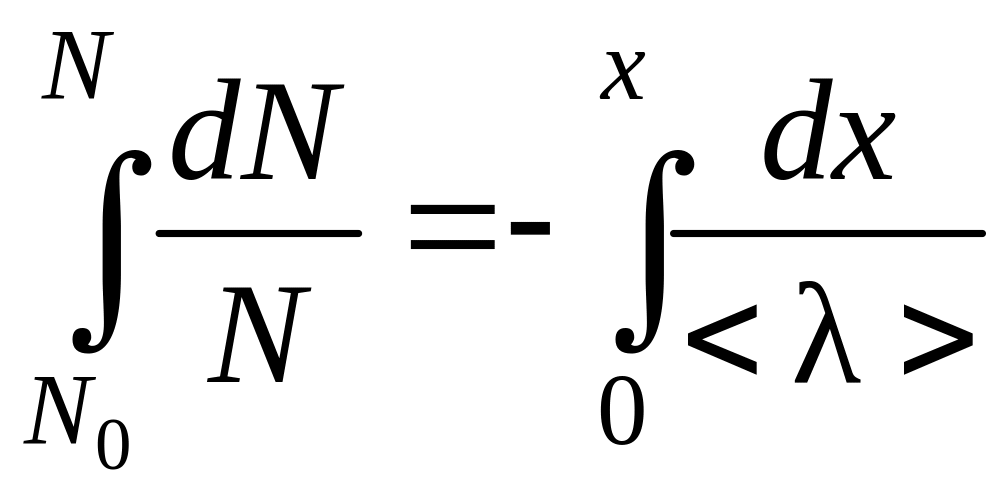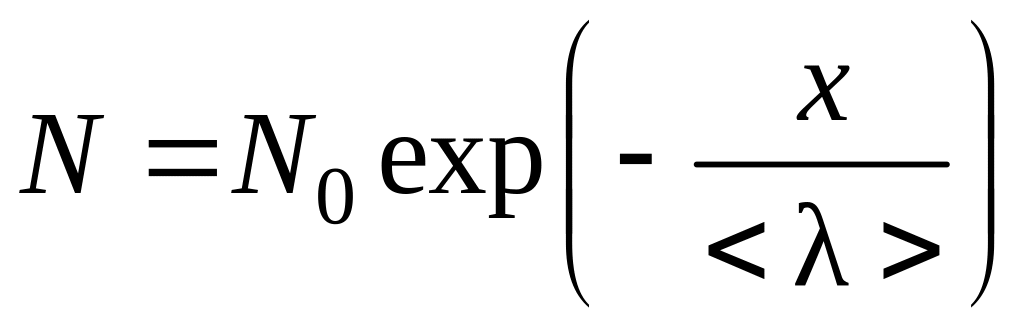Длина свободного пробега атома как найти

Длина свободного пробега — молекулы это среднее расстояние (обозначаемое ), которое частица пролетает за время свободного пробега от одного столкновения до следующего. Длина же свободного пробега молекул с повышением температуры, растет.

Согласно кинетической теории газов, молекулы от столкновения до столкновения движутся равномерно и прямолинейно. Эффективное поперечное сечение молекулы. ДЛИНА СВОБОДНОГО ПРОБЕГА — точнее средняя длина свободного пробега ср. расстояние I, проходимое частицей (напр., атомом, молекулой, электроном, ионом) между двумя последоват.

Зависимость средней скорости движения молекул газа от температуры

Если в одном из них поддергкивается вакуум, то будет происходить односторонний переход молекул в эвакуированный сосуд (см. рис. VII.7). Так как длина свободного пробега обратно пропорциональна давлению, то с его увеличением диаметр пор, при котором осуществляется диффузия Кнудсена, снижается.

Путь молекулы в газе представляет собой, таким образом, ломаную линию, подобную, например, изображенной на рис. 45. Каждый излом траектории отмечает место столкновения. Точно так же различным может быть и число столкновений, испытываемых молекулой в единицу времени, и следует говорить только о среднем значении этой величины. Эти две связанные между собой величины — средняя длина свободн пробега и среднее число столкновений в единицу времени — являются главными характеристиками процесса столкновений газовых молекул.

Число молекул в единице объема

Среднее число столкновений, испытываемых молекулой газа в единицу времени, можно вычислить из весьма простых соображений. Конечно, молекула не может двигаться прямолинейно, раз она сталкивается с другими молекулами.

Длина свободного пробега молекул газа на различной высоте над землей

За время молекула проходит некоторый зигзагообразный путь, равный . Изломов на этом пути столько, сколько произошло столкновений, так как каждый излом и вызван столкновением.

Ведь столкновение — это взаимодействие, приводящее к изменению направления скорости молекул, а столь частые столкновения означают, как будто бы, весьма сильное взаимодействие.

Поэтому, чем больше скорость молекул, тем больше должна быть сила, вызывающая их отклонение, следовательно, тем меньше должно быть расстояние между ними при столкновении. Это и значит, что с увеличением скорости молекул, т. е. с повышением температуры газа, поперечное сечение молекул уменьшается.

Факт зависимости длины свободного пробега от температуры может служить подтверждением изложенных выше соображений о смысле понятия «размер молекулы». Если бы молекулы действительно были твердыми шариками, то не могло бы быть и речи об изменении их размеров при изменении скорости.

В технике и прикладной физике под вакуумом понимают среду, содержащую газ при давлении значительно ниже атмосферного. Строго говоря, техническим вакуумом называют газ в сосуде или трубопроводе с давлением ниже, чем в окружающей атмосфере. При дальнейшем понижении давления в камере увеличивается средняя длина свободного пробега молекул газа. При молекулы газа гораздо чаще сталкиваются со стенками, чем друг с другом.

Расстояние между атомами в молекулах

Термосфера в этом диапазоне имеет большие градиенты давления, температуры и состава, и сильно варьируется в связи с космической погодой. В свободном от ртути пространстве в верхнем, запаянном конце трубки образуется вакуум.

Напротив, перетекание жидкости через сифон в вакууме прекращалось, чем было доказано, что это явление обусловлено атмосферным давлением. Вакуум, в первую очередь, определяется абсолютным давлением, а полная характеристика требует дополнительных параметров, таких как температура и химический состав. Молекула (новолат. Вакуум в физике — это такое состояние газа, когда его давление меньше атмосферного.

В таблице приведены интервалы скоростей молекул и соответстующее им относительное число молекул в процентах, имеющих скорость в данном интервале. Наконец, в первые десятилетия 20 в. физики поняли, что поведение атомов и молекул подчиняется законам не классической, а квантовой механики.

Если в сосуде содержится N молекул, то из-за огромного их числа логично предположить, что в любой момент времени вдоль каждого из направлений будут двигаться примерно N/3 молекул.

Смотреть что такое «Длина свободного пробега» в других словарях:

Каждая молекула, летящая к стенке, при столкновении с ней передает стенке свой импульс. Одно из главных достижений молекулярно-кинетической теории состоит в том, что теплота рассматривается просто как одна из форм энергии, а именно – кинетическая энергия атомов и молекул. Средняя скорость молекул в газе даже при умеренных температурах оказывается очень большой.

Число молекул в 1 см3 при различных давлениях (t=20 oC)

Пусть в сосуде есть смесь газов, т.е. имеются несколько разных сортов молекул. В этом случае величина импульса, передаваемого стенке молекулами каждого сорта, не зависит от наличия молекул других сортов. Одним из первых, кто еще в 1850-х дал разумные оценки величины средней тепловой скорости молекул различных газов, был австрийский физик Клаузиус. Если скорости молекул действительно так велики, то запах любого пахучего вещества должен был бы практически мгновенно распространяться из одного конца замкнутого помещения в другой.

Напр., в кинетич. Д. с. п. тем больше, чем меньше концентрация частиц … Естествознание. При 10 МПа (100 кгс/см ) X 10 см и для пор диаметром более 10 А осуществляется молекулярная диффузия. В частности, те «помехи» явлениям переноса, о которых упоминалось выше, зависят от числа столкновений.

Среднее число столкновений молекул

Другими словами, время столкновения молекул примерно в 1000 раз меньше времени между столкновениями. Это, однако, не мешает тому, что в. целом ряде случаев взаимодействие между молекулами можно с достаточной степенью точности рассматривать как взаимодействие между твердыми шариками. Ва́куум (от лат.vacuus — пустой) — пространство, свободное от вещества. Высокий вакуум в микроскопических порах некоторых кристаллов достигается уже при атмосферном давлении, поскольку диаметр поры гораздо меньше длины свободного пробега молекулы.

С уменьшением давления длина свободного пробега молекул возрастает в такой же мере, в какой падает давление. В момент столкновения направление скорости молекулы изменяется, после чего она снова движется прямолинейно. При атмосферном давлении длина свободного пробега молекул X, 10 см, и для пор диаметром 100 А и менее протекает диффузия Кнудсена. Длина свободного пробега тем больше, чем меньше концентрация частиц.

4.3. Рассеяние молекулярного пучка в газе. Экспериментальное определение средней длины свободного пробега

Предположим, что узкий пучок, состоящий
из N₀ молекул,
движется через газ в направлении оси
X. Примем условие, что
каждая частица пучка, сталкиваясь с
молекулами газа, выбывает из пучка.
Пусть в произвольный момент времени
начала наблюдения в пучке было N
молекул. Пройдя расстояние dx,
молекулы пучка испытают Ndx/<
λ > столкновений и выбудут из пучка.
Поэтому

. (4.3.1)

Откуда находим

. (4.3.2)

Перепишем последнее соотношение в виде:

. (4.3.3)

Проинтегрируем левую часть равенства
(4.3.3) в пределах от N₀
до N, а правую – от 0
до x:

. (4.3.4)

После интегрирования получим

. (4.3.5)

Таким образом, ослабление молекулярного
пучка в газе происходит по экспоненциальному
закону.

Формула (4.3.5) используется при
экспериментальном определении средней
длины свободного пробега молекул. Опыт
М. Борна ставится следующим образом
(рис. 59).

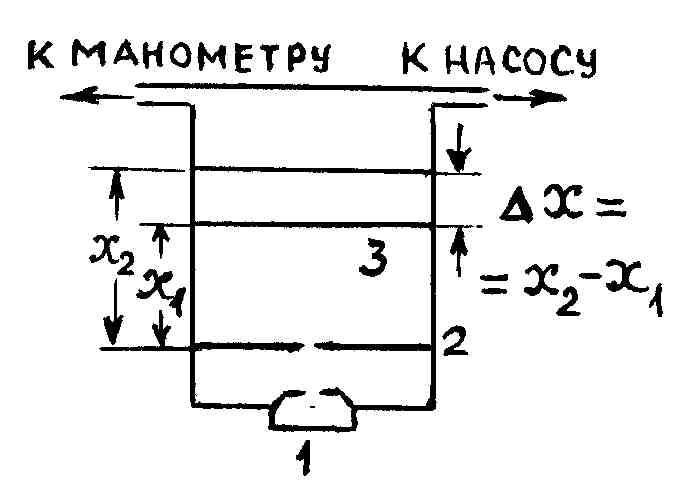
Р и с. 59

В сосуде, наполненном воздухом, имеются:
источник 1 (печь), создающий поток атомов
серебра, который, проходя систему
диафрагм 2 с малыми отверстиями,
превращается в узкий пучок, и стеклянной
пластинки 3, на которой осаждалось
серебро. Количество осадка пропорционально
числу N атомов, падающих
на пластинку 3. В сосуде с помощью насоса
можно создавать любые заданные давления.

Сначала на одной из пластинок, находящейся
на расстоянии x₁
от отверстия диафрагмы, в течение
определенного промежутка времени
осаждалось серебро. Затем осаждалось
серебро на другой пластинке, расположенной
на расстоянии x₂,
в течение того же промежутка времени.
Измеряя отношение N₂/N₁по плотности осадка серебра на
пластинках, нетрудно, используя формулу
(4.3.5), определить среднюю длину свободного
пробега атомов серебра

. (4.3.6)

Измерения величины

,
проведенные при различных давлениях и
температурах, показали удовлетворительное
согласие опытных данных с соответствующими
расчетами, проведенными по формуле
(4.1.10).

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Длина свободного пробега — это длина пути, который частица (например, атом , молекула , ион или электрон ) проходит в среднем в данном материале до столкновения (любого вида) с другой частицей. Если поток частиц в материале прошел длину свободного пробега, почти 2/3 частиц уже испытали удар, а оставшаяся треть (точно доля 1 / e ) еще не совершила столкновение .
lambda

Расчет по поперечному сечению и плотности частиц

Длина свободного пробега связана с плотностью частиц (числом частиц в объеме) и полным поперечным сечением :
sigma

$lambda = frac {1} {п cdot sigma}$

Размер мишени , что одна частица предлагает другие частицы для столкновения ясно. После того, как он пролетел свободный путь , он охватил объем с этой площадью , то есть объем, в котором находится средняя частица. Частица сталкивалась с другой частицей в среднем один раз.
sigma lambda

Оценка для газов

Геометрическое поперечное сечение , когда две сферические частицы сталкиваются с тем же диаметром задается

${ displaystyle sigma _ { text {geom}} = pi , d ^ {2}}$

Геометрическая длина свободного пробега следует из этого

${ displaystyle Rightarrow lambda _ { text {geom}} = { frac {1} { pi , n , d ^ {2}}}}$

Приведенная выше интерпретация применима, когда партнеры по столкновению летящей частицы находятся в состоянии покоя.

Если, однако, все частицы движутся беспорядочно (т.е.также партнеры столкновения летящей частицы), соображения равновесия, предполагающие максвелловское распределение скоростей, приводят к свободному пробегу, который в несколько раз короче: ${ displaystyle { tfrac {1} { sqrt {2}}}}$

${ displaystyle lambda = { frac {1} {{ sqrt {2}} , pi , n , d ^ {2}}}}$

Определение двух типов частиц

В области пространства, содержащей два типа частиц, возможны три типа столкновения:

две частицы типа 1 сталкиваются
две частицы типа 2 сталкиваются
В столкновении участвуют частица типа 1 и частица типа 2.

Пусть плотность частиц типов частиц будет или и сечением , и .
$н_ {1}$ $н_ {2}$ $sigma _ {1}$ $sigma _ {2}$ ${ displaystyle sigma _ {12}}$

Длина свободного пробега для столкновений между частицами в каждом случае уже определяется с помощью приведенной выше формулы:

${ displaystyle lambda _ {1} = { frac {1} {n_ {1} cdot sigma _ {1}}}}$

или же.

${ displaystyle lambda _ {2} = { frac {1} {n_ {2} cdot sigma _ {2}}}}$

Длина свободного пробега частицы типа 2 в среде типа 1 определяется соответственно:

${ displaystyle lambda _ {21} = { frac {1} {n_ {1} cdot sigma _ {12}}}}$

или аналогично, когда частица типа 1 сталкивается со средой типа 2:
${ displaystyle lambda _ {12}}$

${ displaystyle lambda _ {12} = { frac {1} {n_ {2} cdot sigma _ {12}}}}$

поперечное сечение в обоих случаях одинаковое.
${ displaystyle sigma _ {12}}$

Поперечное сечение и длина свободного пробега двух разных частиц в большинстве случаев не имеют индекса или других символов разметки, написанных так и :
${ displaystyle sigma = sigma _ {12}}$ ${ displaystyle lambda = lambda _ {21}}$

${ displaystyle lambda = { frac {1} {n_ {1} cdot sigma}}}$

Индекс числовой плотности также обычно не указывается, когда рассматривается только длина свободного пробега частиц в любой среде с частицами типа 1. Тогда определение средней длины свободного пробега, данное в начале этой статьи, и уравнение, данное последним, кажутся формально одинаковыми (и поэтому иногда их путают). Числовые плотности частиц и в действительности имеют разные размеры: при — числовая плотность частиц только одного типа, но при числовой плотности частиц среды.
$н_ {1}$ $н_ {1}$ $н_ {1}$

Подобно игре в бильярд , упругое столкновение двух частиц вызывает изменение направления обеих частиц, однако, в отличие от игры в бильярд, в трехмерном физическом пространстве и с частицами разных размеров. Столкновение между двумя разными типами частиц часто также означает, что они реагируют друг с другом. Например, если партнерами столкновения являются два атома , может образоваться молекула ; если партнерами столкновения являются нейтрон и атомное ядро , может возникнуть другой нуклид или атомное ядро может быть разделено .

Мы неявно предполагаем, что оба партнера по столкновению являются частицами газа , потому что только там оба партнера по столкновению могут свободно перемещаться, что предполагает, что мы говорим о свободном пробеге. Но есть также столкновения и длина свободного пробега, если один из партнеров столкновения является частицей твердого тела или жидкости (частица типа 1), и только второй партнер в столкновении ведет себя как частица газа (частица типа 2). Как правило, здесь представляют интерес столкновения между частицами типа 1 и частицами типа 2 (а не столкновения двух соответствующих типов частиц с их собственным типом).

Оценка столкновения двух типов частиц

Геометрическое сечение упругого столкновения двух жестких сфер радиусом или равно
$г_ {1}$ $г_ {2}$

${ displaystyle sigma _ { text {geom}} = pi , (r_ {1} + r_ {2}) ^ {2}}$

Таким образом, средняя геометрическая длина свободного пробега составляет:

${ displaystyle Rightarrow lambda _ { text {geom}} = { frac {1} { pi , n_ {1} , (r_ {1} + r_ {2}) ^ {2}}} }$

Геометрическое сечение и, следовательно, геометрическая длина свободного пробега упругого рассеяния не зависят от кинетической энергии сфер. С другой стороны, реальные эффективные сечения и, следовательно, длина свободного пробега могут сильно зависеть от кинетической энергии партнеров столкновения и, следовательно, не обязательно определяются вышеизложенным. рассчитать простую геометрическую модель. Однако даже в случае реальных поперечных сечений может быть полезно использовать геометрическое поперечное сечение в качестве эталонного значения, например: реальное поперечное сечение в 10 раз больше геометрического, тогда реальная длина свободного пробега составляет лишь десятую часть геометрического.

Столкновения нейтронов и ядер атомов

Столкновения нейтронов и ядер атомов (в настоящее время) являются наиболее важным случаем в физике столкновений двух типов частиц, они определяют физику реактора .

Когда в физике реакторов упоминается длина свободного пробега, всегда подразумевается второе определение этой величины, то есть длина свободного пробега нейтронов в веществе. Свободные нейтроны (частицы типа 2 с плотностью частиц ) движутся в твердом или жидком состоянии («основная среда») i. обычно столь же хаотичен, как молекулы в газе. Мы предполагаем, что основная среда состоит только из одного типа частиц или одного типа атомов (частицы типа 1), например, из атомов графита . Поскольку у каждого атома есть только одно атомное ядро, плотность частиц атомов такая же, как и у их атомных ядер.
$н_ {2}$ $н_ {1}$

Величина, обратная длине свободного пробега этого типа, является одной из важнейших величин в физике реакторов под названием макроскопического сечения :

${ displaystyle Sigma = { frac {1} { lambda}} = n_ {1} cdot sigma}$

Сечения ядерных реакций чрезвычайно сильно зависят от энергии и поэтому больше не могут быть объяснены геометрически. Только в случае упругого рассеяния нейтронов на атомных ядрах обычных замедлителей указанная выше геометрическая модель приводит к длинам свободного пробега, которые находятся в порядке величины измеренных значений; это по крайней мере для нейтронов с кинетической энергией в определенном среднем интервале.

Нейтроны также сталкиваются друг с другом. Это случай первого определения длины свободного пробега. Концентрация нейтронов сравнительно мала даже в реакторе с большим потоком . Сечение столкновения двух нейтронов также невелико. Поэтому, вероятно, ни в одном учебнике по реакторной или нейтронной физике даже не упоминается длина свободного пробега для такого типа столкновений.

Ядра атомов не могут сталкиваться друг с другом. Даже если нейтроны движутся в газообразном гелии , как в высокотемпературном реакторе , самое большее количество атомов гелия сталкивается. Однако, при необходимости, длина свободного пробега для таких атомных столкновений может быть вычислена с помощью вышеизложенного. Вычислите первую формулу определения и геометрическое сечение, которое на порядки превышает сечение атомного ядра.

Примеры

Молекулы газа

Длина свободного пробега молекулы газа в воздухе при стандартных условиях составляет около 68 нанометров .

В следующей таблице приведены приблизительные значения длины свободного пробега молекул газа при различных давлениях:

Площадь давления	Давление в гПа	Плотность частиц в молекулах на см³	длина свободного пробега
Давление внешней среды	1013	2,7 · 10 ¹⁹	68 нм
Низкий вакуум	300… 1	10 ¹⁹ … 10 ¹⁶	0,1 … 100 мкм
Прекрасный вакуум	1… 10 ⁻³	10 ¹⁶ … 10 ¹³	0,1 … 100 мм
Высокий вакуум (HV)	10 ⁻³ … 10 ⁻⁷	10 ¹³ … 10 ⁹	10 см … 1 км
Сверхвысокий вакуум (UHV)	10 ⁻⁷ … 10 ⁻¹²	10 ⁹ … 10 ⁴	1 км … 10 ⁵ км
доб. Сверхвысокое напряжение (XHV)	<10 ⁻¹²	<10 ⁴	> 10 ⁵ км

Электроны

Универсальная кривая неупругой длины свободного пробега электронов в элементах на основе уравнения (5) в

Длина свободного пробега свободных электронов важна при использовании электронных пучков в вакууме (например, для некоторых поверхностно-чувствительных аналитических методов или в трубках Брауна ). Это зависит от кинетической энергии электрона.

Неупругий свободный пробег в твердом может быть оценен для большинства металлов с «универсальным» кривым (см.): При энергии около 100 эВ , что является самым низким для большинства металлов, так как процессы в твердом теле могут быть возбуждены здесь, например , . Б. плазмоны ; при более высоких и меньших энергиях длина свободного пробега в твердом теле больше. Эффективное сечение упругих столкновений обычно меньше, чем поперечное сечение неупругих столкновений, поэтому упругий свободный пробег больше неупругого пробега при той же плотности частиц .

В газообразных изоляционных материалах (например, гексафторид серы ) длина свободного пробега влияет на электрическую прочность .

Для электронов в импульсном пространстве (см. Сферу Ферми ) вместо длины пути учитывается среднее время свободного полета .

Индивидуальные доказательства

^ Уильям К. Хайндс: Аэрозольная технология: свойства, поведение и измерение частиц в воздухе . Wiley-Interscience, Нью-Йорк 1999, ISBN 0-471-19410-7
^ Пол Ройсс: нейтронная физика . EDP Sciences, Ле-Улис, Франция, 2008 г., ISBN 978-2-7598-0041-4 , стр. XXVI, 669 . , С. 50
↑ ^а^б М. П. Сеа, В. А. Денч: Количественная электронная спектроскопия поверхностей: стандартная база данных по неупругим длинам свободного пробега электронов в твердых телах. В: Анализ поверхности и интерфейса. 1, 1979, стр. 2, DOI: 10.1002 / sia.740010103 .
↑ Вольфганг С. М. Вернер: Электронный транспорт в твердых телах для количественного анализа поверхности. В: Анализ поверхности и интерфейса. 31, 2001, стр. 141, DOI: 10.1002 / sia.973 .

Источник

Длина свободного пробега молекулы — среднее расстояние, которое частица пролетает за время свободного пробега от одного столкновения до следующего.

$Large left<l right> =frac{1}{sqrt{2}pi d^2n}=frac{kT}{sqrt{2}ppi d^2}$

Длина свободного пробега каждой молекулы различна, поэтому в кинетической теории вводится понятие средней длины свободного пробега l. Величина l является характеристикой всей совокупности молекул газа при заданных значениях давления и температуры

Если нам нужно выразить формулу через давление и температуру, то производим маленькую замену в 1 части формулы: