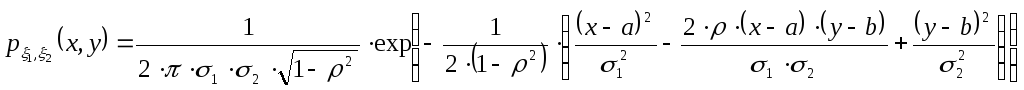Дисперсия матрицы как найти

Дано:

1. Вычисление вектора мат. ожиданий и
   ковариационных характеристик

случайного вектора:

• 1 способ

Для вычисления мат. ожиданий преобразуем
выражение, стоящее под экспонентой,
методом Лагранжа:

Значит вектор мат. ожиданий имеет вид:
.

Для нахождения дисперсий и коэффициента
корреляции сопоставим исходную плотность
распределения с общей формулой.

Откуда получим следующую систему:

• 2 способ

Найдем сначала неизвестную константу
исходя из следующих соображений:

,
т.е.

и

Найдем теперь вектор мат. ожиданий.

Имеем

Следовательно плотности распределения
имеют вид:

Откуда получен вектор мат. ожиданий
.

Ковариационную матрицу мы можем найти
также 2-мя способами:

• 1 способ

Ковариационная матрица – это матрица,
обратная матрице квадратичной формы.

Матрица квадратичной формы:
;

Матрица ковариации:
.

• 2 способ

Найдем 1 и 4 элемент матрицы ковариационной
матрицы как дисперсии:

А 2 и 3 элементы равны и находятся по
формуле
.

Найдем
.

Тогда второй и третий элементы будут
равны:
.

Имеем матрицу ковариации:
,
что совпало с вычисленной первым способом
матрицей.

1. Найти ортогональное преобразование,
   переводящее соответствующий центрированный
   случайный вектор в вектор с независимыми
   компонентами.

Преобразование описывается следующим
образом:
,
где A – ортогональная
матрица, а B — вектор.
Матрица A — матрица перехода
от стандартного базиса к базису
собственных векторов нашей матрицы
квадратичной формы.

т.к. ковариационная матрица уже
диагональная. Эта матрица ортогональна,
следовательно, ортогонально и
преобразование. Для центрирования
данного случайного вектора надо отнять
столбец математических ожиданий данных
компонент, т.е.
.

Тогда квадратичная форма станет:

Якобиан такой замены будет равен 1.

Следовательно, после такой замены,
плотность случайного вектора принимает
вид:

Данный вектор центрирован (математическое
ожидание обоих компонент равно 0), имеет
независимые друг от друга компоненты
и получен ортогональным преобразованием.

Из такого вектора легко получить
стандартный нормальный вектор. Достаточно
сделать ещё одну замену.

На диагонали всегда будут находиться
члены вида
.
Якобиан такой замены будет:

И умножив плотность распределения

т. е. компонент предыдущей замены получим

— плотность распределения стандартного
и центрированного вектора.

1. Вычислить характеристики совместного
   распределения с.в.
   
   и записать его плотность.

За счет линейности мат. ожидания получим:

За счет независимости компонент можно
рассчитать дисперсии следующим образом:

Теперь вычислим ковариации новых
компонент вектора.

в силу независимости компонент.

Отсюда, матрица ковариации:
.

Записываем плотность нового случайного
вектора

,
где
.

Подставив все значения, получим:

.

Для проверки распределения составим
матрицу квадратичной формы,
,

и найдем обратную к ней:
— получили матрицу ковариации, что
подтверждает верность наших расчетов.

Соседние файлы в папке ТВ

• #
• #
• #

Как найти дисперсию?

Дисперсия — это мера разброса значений случайной величины $X$ относительно ее математического ожидания $M(X)$ (см. как найти математическое ожидание случайной величины). Дисперсия показывает, насколько в среднем значения сосредоточены, сгруппированы около $M(X)$: если дисперсия маленькая — значения сравнительно близки друг к другу, если большая — далеки друг от друга (см. примеры нахождения дисперсии ниже).

Если случайная величина описывает физические объекты с некоторой размерностью (метры, секунды, килограммы и т.п.), то дисперсия будет выражаться в квадратных единицах (метры в квадрате, секунды в квадрате и т.п.). Ясно, что это не совсем удобно для анализа, поэтому часто вычисляют также корень из дисперсии — среднеквадратическое отклонение $sigma(X)=sqrt{D(X)}$, которое имеет ту же размерность, что и исходная величина и также описывает разброс.

Еще одно формальное определение дисперсии звучит так: «Дисперсия — это второй центральный момент случайной величины» (напомним, что первый начальный момент — это как раз математическое ожидание).

Формула дисперсии случайной величины

Дисперсия случайной величины Х вычисляется по следующей формуле:
$$
D(X)=M(X-M(X))^2,
$$
которую также часто записывают в более удобном для расчетов виде:
$$
D(X)=M(X^2)-(M(X))^2.
$$

Эта универсальная формула для дисперсии может быть расписана более подробно для двух случаев.

Если мы имеем дело с дискретной случайной величиной (которая задана перечнем значений $x_i$ и соответствующих вероятностей $p_i$), то формула принимает вид:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2.
$$
Если же речь идет о непрерывной случайной величине (заданной плотностью вероятностей $f(x)$ в общем случае), формула дисперсии Х выглядит следующим образом:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$

Пример нахождения дисперсии

Рассмотрим простые примеры, показывающие как найти дисперсию по формулам, введеным выше.

Пример 1. Вычислить и сравнить дисперсию двух законов распределения:
$$
x_i quad 1 quad 2 \
p_i quad 0.5 quad 0.5
$$
и
$$
y_i quad -10 quad 10 \
p_i quad 0.5 quad 0.5
$$

Для убедительности и наглядности расчетов мы взяли простые распределения с двумя значениями и одинаковыми вероятностями. Но в первом случае значения случайной величины расположены рядом (1 и 2), а во втором — дальше друг от друга (-10 и 10). А теперь посмотрим, насколько различаются дисперсии:
$$
D(X)=sum_{i=1}^{n}{x_i^2 cdot p_i}-left(sum_{i=1}^{n}{x_i cdot p_i} right)^2 =\
= 1^2cdot 0.5 + 2^2 cdot 0.5 — (1cdot 0.5 + 2cdot 0.5)^2=2.5-1.5^2=0.25.
$$
$$
D(Y)=sum_{i=1}^{n}{y_i^2 cdot p_i}-left(sum_{i=1}^{n}{y_i cdot p_i} right)^2 =\
= (-10)^2cdot 0.5 + 10^2 cdot 0.5 — (-10cdot 0.5 + 10cdot 0.5)^2=100-0^2=100.
$$
Итак, значения случайных величин различались на 1 и 20 единиц, тогда как дисперсия показывает меру разброса в 0.25 и 100. Если перейти к среднеквадратическому отклонению, получим $sigma(X)=0.5$, $sigma(Y)=10$, то есть вполне ожидаемые величины: в первом случае значения отстоят в обе стороны на 0.5 от среднего 1.5, а во втором — на 10 единиц от среднего 0.

Ясно, что для более сложных распределений, где число значений больше и вероятности не одинаковы, картина будет более сложной, прямой зависимости от значений уже не будет (но будет как раз оценка разброса).

Пример 2. Найти дисперсию случайной величины Х, заданной дискретным рядом распределения:
$$
x_i quad -1 quad 2 quad 5 quad 10 quad 20 \
p_i quad 0.1 quad 0.2 quad 0.3 quad 0.3 quad 0.1
$$

Снова используем формулу для дисперсии дискретной случайной величины:
$$
D(X)=M(X^2)-(M(X))^2.
$$
В случае, когда значений много, удобно разбить вычисления по шагам. Сначала найдем математическое ожидание:
$$
M(X)=sum_{i=1}^{n}{x_i cdot p_i} =-1cdot 0.1 + 2 cdot 0.2 +5cdot 0.3 +10cdot 0.3+20cdot 0.1=6.8.
$$
Потом математическое ожидание квадрата случайной величины:
$$
M(X^2)=sum_{i=1}^{n}{x_i^2 cdot p_i}
= (-1)^2cdot 0.1 + 2^2 cdot 0.2 +5^2cdot 0.3 +10^2cdot 0.3+20^2cdot 0.1=78.4.
$$
А потом подставим все в формулу для дисперсии:
$$
D(X)=M(X^2)-(M(X))^2=78.4-6.8^2=32.16.
$$
Дисперсия равна 32.16 квадратных единиц.

Пример 3. Найти дисперсию по заданному непрерывному закону распределения случайной величины Х, заданному плотностью $f(x)=x/18$ при $x in(0,6)$ и $f(x)=0$ в остальных точках.

Используем для расчета формулу дисперсии непрерывной случайной величины:
$$
D(X)=int_{-infty}^{+infty} f(x) cdot x^2 dx — left( int_{-infty}^{+infty} f(x) cdot x dx right)^2.
$$
Вычислим сначала математическое ожидание:
$$
M(X)=int_{-infty}^{+infty} f(x) cdot x dx = int_{0}^{6} frac{x}{18} cdot x dx = int_{0}^{6} frac{x^2}{18} dx =
left.frac{x^3}{54} right|_0^6=frac{6^3}{54} = 4.
$$
Теперь вычислим
$$
M(X^2)=int_{-infty}^{+infty} f(x) cdot x^2 dx = int_{0}^{6} frac{x}{18} cdot x^2 dx = int_{0}^{6} frac{x^3}{18} dx = left.frac{x^4}{72} right|_0^6=frac{6^4}{72} = 18.
$$
Подставляем:
$$
D(X)=M(X^2)-(M(X))^2=18-4^2=2.
$$
Дисперсия равна 2.

Другие задачи с решениями по ТВ

Вычисление дисперсии онлайн

Как найти дисперсию онлайн для дискретной случайной величины? Используйте калькулятор ниже.

• Введите число значений случайной величины К.
• Появится форма ввода для значений $x_i$ и соответствующих вероятностей $p_i$ (десятичные дроби вводятся с разделителем точкой, например: -10.3 или 0.5). Введите нужные значения (проверьте, что сумма вероятностей равна 1, то есть закон распределения корректный).
• Нажмите на кнопку «Вычислить».
• Калькулятор покажет вычисленное математическое ожидание $M(X)$ и затем искомое значение дисперсии $D(X)$.

Видео. Полезные ссылки

Видеоролики: что такое дисперсия и как найти дисперсию

Если вам нужно более подробное объяснение того, что такое дисперсия, как она вычисляется и какими свойствами обладает, рекомендую два видео (для дискретной и непрерывной случайной величины соответственно).

Полезные ссылки

Не забывайте сначала прочитать том, как найти математическое ожидание. А тут можно вычислить также СКО: Калькулятор математического ожидания, дисперсии и среднего квадратического отклонения.

Что еще может пригодиться? Например, для изучения основ теории вероятностей — онлайн учебник по ТВ. Для закрепления материала — еще примеры решений задач по теории вероятностей.

А если у вас есть задачи, которые надо срочно сделать, а времени нет? Можете поискать готовые решения в решебнике или заказать в МатБюро:

  Перевод

  Ссылка на автора

Фундаментальная статистика — полезный инструмент в прикладном машинном обучении для лучшего понимания ваших данных.

Они также являются инструментами, которые обеспечивают основу для более продвинутых операций линейной алгебры и методов машинного обучения, таких как ковариационная матрица и анализ главных компонентов соответственно. Как таковой, важно иметь сильную власть над фундаментальной статистикой в ​​контексте обозначений линейной алгебры.

В этом руководстве вы узнаете, как работают основные статистические операции и как их реализовывать с использованием NumPy с обозначениями и терминологией из линейной алгебры.

После завершения этого урока вы узнаете:

• Каковы ожидаемые значения, среднее значение и среднее значение и как их рассчитать.
• Что такое дисперсия и стандартное отклонение и как их рассчитать.
• Что такое ковариационная, корреляционная и ковариационная матрицы и как их вычислять.

Давайте начнем.

• Обновлено март / 2018: Исправлена ​​небольшая опечатка в результате для примера с векторной дисперсией. Спасибо Боб.

Обзор учебника

Этот урок разделен на 4 части; они есть:

1. Ожидаемое значение
2. отклонение
3. ковариации
4. Ковариационная матрица

Ожидаемое значение

По вероятности, среднее значение некоторой случайной величины X называется ожидаемым значением или ожиданием.

Ожидаемое значение использует обозначение E в квадратных скобках вокруг имени переменной; например:

E[X]

Он рассчитывается как взвешенная по вероятности сумма значений, которые можно нарисовать.

E[X] = sum(x1 * p1, x2 * p2, x3 * p3, ..., xn * pn)

В простых случаях, таких как подбрасывание монеты или бросание игральных костей, вероятность каждого события столь же вероятна. Следовательно, ожидаемое значение может быть рассчитано как сумма всех значений, умноженная на обратную величину количества значений.

E[X] = sum(x1, x2, x3, ..., xn) . 1/n

В статистике среднее или, точнее говоря, среднее арифметическое или выборочное среднее можно оценить по выборке примеров, взятых из области. Это сбивает с толку, потому что среднее, среднее и ожидаемое значение используются взаимозаменяемо.

В аннотации среднее значение обозначается строчной греческой буквой mu и рассчитывается по выборке наблюдений, а не по всем возможным значениям.

mu = sum(x1, x2, x3, ..., xn) . 1/n

Или написано более компактно:

mu = sum(x . P(x))

Где x — вектор наблюдений, а P (x) — расчетная вероятность для каждого значения.

При вычислении для конкретной переменной, такой как x, среднее значение обозначается как имя переменной в нижнем регистре со строкой выше, называемой x-bar.

_
x = sum from 1 to n (xi) . 1/n

Среднее арифметическое можно рассчитать для вектора или матрицы в NumPy с помощью функции mean ().

В приведенном ниже примере определяется 6-элементный вектор и вычисляется среднее значение.

from numpy import array
from numpy import mean
v = array([1,2,3,4,5,6])
print(v)
result = mean(v)
print(result)

При запуске примера сначала печатается определенный вектор и среднее значение в векторе.

[1 2 3 4 5 6]

3.5

Функция среднего значения может вычислить средние значения строки или столбца матрицы, указав аргумент оси и значение 0 или 1 соответственно.

В приведенном ниже примере определяется матрица 2 × 6 и вычисляются средние значения столбца и строки.

from numpy import array
from numpy import mean
M = array([[1,2,3,4,5,6],[1,2,3,4,5,6]])
print(M)
col_mean = mean(M, axis=0)
print(col_mean)
row_mean = mean(M, axis=1)
print(row_mean)

При выполнении примера сначала печатается определенная матрица, затем вычисленные средние значения столбца и строки.

[[1 2 3 4 5 6]
 [1 2 3 4 5 6]]

[ 1.  2.  3.  4.  5.  6.]

[ 3.5  3.5]

отклонение

По вероятности, дисперсия некоторой случайной величины X является мерой того, насколько значения в распределении варьируются в среднем по отношению к среднему.

Дисперсия обозначается как функция Var () для переменной.

Var[X]

Дисперсия рассчитывается как среднеквадратическая разница каждого значения в распределении от ожидаемого значения. Или ожидаемое квадратичное отличие от ожидаемого значения.

Var[X] = E[(X - E[X])^2]

Предполагая, что ожидаемое значение переменной было вычислено (E [X]), дисперсия случайной величины может быть рассчитана как сумма квадратов разности каждого примера от ожидаемого значения, умноженного на вероятность этого значения.

Var[X] = sum (p(x1) . (x1 - E[X])^2, p(x2) . (x2 - E[X])^2, ..., p(x1) . (xn - E[X])^2)

Если вероятность каждого примера в распределении равна, вычисление дисперсии может отбросить отдельные вероятности и умножить сумму квадратов разностей на обратную величину количества примеров в распределении.

Var[X] = sum ((x1 - E[X])^2, (x2 - E[X])^2, ...,(xn - E[X])^2) . 1/n

В статистике дисперсию можно оценить из выборки примеров, взятых из домена.

В реферате выборочная дисперсия обозначается сигмой в нижнем регистре с 2 верхними индексами, указывающими, что единицы возведены в квадрат, а не то, что вы должны возвести в квадрат окончательное значение. Сумма квадратов разностей умножается на обратную величину количества примеров минус 1, чтобы скорректировать смещение.

sigma^2 = sum from 1 to n ( (xi - mu)^2 ) . 1 / (n - 1)

В NumPy дисперсию можно рассчитать для вектора или матрицы с помощью функции var (). По умолчанию функция var () вычисляет дисперсию населения. Чтобы вычислить выборочную дисперсию, вы должны установить аргумент ddof в значение 1.

В приведенном ниже примере определяется 6-элементный вектор и вычисляется выборочная дисперсия.

from numpy import array
from numpy import var
v = array([1,2,3,4,5,6])
print(v)
result = var(v, ddof=1)
print(result)

При выполнении примера сначала печатается определенный вектор, а затем вычисленная выборочная дисперсия значений в векторе

[1 2 3 4 5 6]

3.5

Функция var может вычислить дисперсию строки или столбца матрицы, указав аргумент оси и значение 0 или 1 соответственно, то же самое, что и средняя функция выше.

В приведенном ниже примере определяется матрица 2 × 6 и рассчитывается выборочная дисперсия столбца и строки.

from numpy import array
from numpy import var
M = array([[1,2,3,4,5,6],[1,2,3,4,5,6]])
print(M)
col_mean = var(M, ddof=1, axis=0)
print(col_mean)
row_mean = var(M, ddof=1, axis=1)
print(row_mean)

При выполнении примера сначала печатается определенная матрица, а затем значения дисперсии выборки столбца и строки.

[[1 2 3 4 5 6]
 [1 2 3 4 5 6]]

[ 0.  0.  0.  0.  0.  0.]

[ 3.5  3.5]

Стандартное отклонение рассчитывается как квадратный корень из дисперсии и обозначается строчными буквами «s».

s = sqrt(sigma^2)

Чтобы придерживаться этого обозначения, иногда дисперсия обозначается как s ^ 2, где 2 — верхний индекс, снова показывая, что единицы возведены в квадрат.

NumPy также предоставляет функцию для вычисления стандартного отклонения напрямую через функцию std (). Как и в случае функции var (), аргумент ddof должен быть установлен в 1 для расчета стандартного отклонения несмещенной выборки, а стандартные отклонения столбца и строки можно рассчитать, установив аргумент оси в 0 и 1 соответственно.

В приведенном ниже примере показано, как рассчитать стандартное отклонение выборки для строк и столбцов матрицы.

from numpy import array
from numpy import std
M = array([[1,2,3,4,5,6],[1,2,3,4,5,6]])
print(M)
col_mean = std(M, ddof=1, axis=0)
print(col_mean)
row_mean = std(M, ddof=1, axis=1)
print(row_mean)

При выполнении примера сначала печатается определенная матрица, а затем значения стандартного отклонения выборки столбца и строки.

[[1 2 3 4 5 6]
 [1 2 3 4 5 6]]

[ 0.  0.  0.  0.  0.  0.]

[ 1.87082869  1.87082869]

ковариации

По вероятности ковариация является мерой совместной вероятности для двух случайных величин. Он описывает, как две переменные изменяются вместе.

Он обозначается как функция cov (X, Y), где X и Y — две рассматриваемые случайные величины.

cov(X,Y)

Ковариация рассчитывается как ожидаемое значение или среднее значение произведения разностей каждой случайной величины от их ожидаемых значений, где E [X] — ожидаемое значение для X, а E [Y] — ожидаемое значение y.

cov(X, Y) = E[(X - E[X] . (Y - E[Y])]

Предполагая, что ожидаемые значения для X и Y были рассчитаны, ковариацию можно рассчитать как сумму разности значений x от их ожидаемого значения, умноженную на разницу значений y от их ожидаемых значений, умноженную на обратную величину числа примеры в популяции.

cov(X, Y) = sum (x - E[X]) * (y - E[Y]) * 1/n

В статистике ковариацию выборки можно рассчитать таким же образом, хотя и с поправкой на смещение, так же, как и с дисперсией.

cov(X, Y) = sum (x - E[X]) * (y - E[Y]) * 1/(n - 1)

Знак ковариации можно интерпретировать как то, увеличиваются ли две переменные вместе (положительно) или уменьшаются вместе (отрицательно). Величина ковариации не легко интерпретируется. Нулевое значение ковариации указывает, что обе переменные полностью независимы.

NumPy не имеет функции для вычисления ковариации между двумя переменными напрямую. Вместо этого у него есть функция для вычисления ковариационной матрицы с именем cov (), которую мы можем использовать для получения ковариации. По умолчанию функция cov () вычисляет несмещенную или выборочную ковариацию между предоставленными случайными величинами.

В приведенном ниже примере определены два вектора одинаковой длины с одним возрастающим и одним убывающим. Мы ожидаем, что ковариация между этими переменными будет отрицательной.

Мы получаем доступ только к ковариации для двух переменных, так как возвращается элемент [0,1] квадратной ковариационной матрицы.

from numpy import array
from numpy import cov
x = array([1,2,3,4,5,6,7,8,9])
print(x)
y = array([9,8,7,6,5,4,3,2,1])
print(y)
Sigma = cov(x,y)[0,1]
print(Sigma)

При запуске примера сначала печатаются два вектора, за которыми следует ковариация значений в двух векторах. Значение является отрицательным, как мы и ожидали.

[1 2 3 4 5 6 7 8 9]
[9 8 7 6 5 4 3 2 1]

-7.5

Ковариация может быть нормализована до значения от -1 до 1, чтобы сделать величину интерпретируемой путем деления ее на стандартное отклонение X и Y. Результат называется корреляцией переменных, также называемой коэффициентом корреляции Пирсона, названным для разработчик метода.

r = cov(X, Y) / sX sY

Где r — коэффициент корреляции X и Y, cov (X, Y) — выборочная ковариация X и Y, а sX и sY — стандартные отклонения X и Y соответственно.

NumPy предоставляет функцию corrcoef () для непосредственного расчета корреляции между двумя переменными. Как и cov (), он возвращает матрицу, в данном случае корреляционную матрицу. Как и в случае результатов cov (), мы можем получить доступ только к корреляции интересов из значения [0,1] из возвращенной квадратной матрицы.

from numpy import array
from numpy import corrcoef
x = array([1,2,3,4,5,6,7,8,9])
print(x)
y = array([9,8,7,6,5,4,3,2,1])
print(y)
Sigma = corrcoef(x,y)
print(Sigma)

При запуске примера сначала печатаются два заданных вектора, за которыми следует коэффициент корреляции. Мы можем видеть, что векторы максимально отрицательно коррелированы, как мы спроектировали.

[1 2 3 4 5 6 7 8 9]
[9 8 7 6 5 4 3 2 1]

-1.0

Ковариационная матрица

Ковариационная матрица представляет собой квадратную и симметричную матрицу, которая описывает ковариацию между двумя или более случайными переменными.

Диагональ ковариационной матрицы — это дисперсии каждой из случайных величин.

Ковариационная матрица является обобщением ковариации двух переменных и отражает то, как все переменные в наборе данных могут изменяться вместе.

Ковариационная матрица обозначается как заглавная греческая буква сигма. Ковариация для каждой пары случайных величин рассчитывается, как указано выше.

Sigma = E[(X - E[X] . (Y - E[Y])]

Куда:

Sigma(ij) = cov(Xi, Xj)

И X — это матрица, в которой каждый столбец представляет случайную величину.

Ковариационная матрица предоставляет полезный инструмент для разделения структурированных отношений в матрице случайных величин Это можно использовать для декорреляции переменных или применять в качестве преобразования к другим переменным. Это ключевой элемент, используемый в методе сокращения данных анализа основных компонентов, или сокращенно PCA.

Ковариационная матрица может быть рассчитана в NumPy с помощью функции cov (). По умолчанию эта функция рассчитывает выборочную ковариационную матрицу.

Функция cov () может быть вызвана с одной матрицей, содержащей столбцы, по которым нужно вычислить ковариационную матрицу, или двумя массивами, например, по одному для каждой переменной.

Ниже приведен пример, который определяет два 9-элементных вектора и вычисляет из них несмещенную ковариационную матрицу.

from numpy import array
from numpy import cov
x = array([1,2,3,4,5,6,7,8,9])
print(x)
y = array([9,8,7,6,5,4,3,2,1])
print(y)
Sigma = cov(x,y)
print(Sigma)

При выполнении примера сначала печатаются два вектора, а затем вычисленная ковариационная матрица.

Значения массивов были придуманы таким образом, чтобы при увеличении одной переменной уменьшалась другая. Мы ожидаем увидеть отрицательный знак ковариации для этих двух переменных, и это то, что мы видим в ковариационной матрице.

[1 2 3 4 5 6 7 8 9]

[9 8 7 6 5 4 3 2 1]

[[ 7.5 -7.5]
 [-7.5  7.5]]

Ковариационная матрица широко используется в линейной алгебре, а пересечение линейной алгебры и статистики называется многомерным анализом. У нас только небольшой вкус в этом посте.

расширения

В этом разделе перечислены некоторые идеи по расширению учебника, которые вы, возможно, захотите изучить.

• Изучите каждый пример, используя свои собственные маленькие надуманные данные.
• Загрузите данные из файла CSV и примените каждую операцию к столбцам данных.
• Напишите свои собственные функции для реализации каждой статистической операции.

Если вы исследуете какое-либо из этих расширений, я хотел бы знать.

Дальнейшее чтение

Этот раздел предоставляет больше ресурсов по теме, если вы хотите углубиться.

книги

• Прикладной многомерный статистический анализ 2012.
• Прикладной многомерный статистический анализ 2015
• Глава 12 Линейная алгебра в вероятности и Статистика, Введение в линейную алгебру, Пятое издание, 2016.
• Глава 3, Теория вероятностей и информации, Глубокое обучение, 2016

API

• Статистические функции NumPy
• API numpy.mean ()
• API numpy.var ()
• API numpy.std ()
• API numpy.cov ()
• API numpy.corrcoef ()

статьи

• Ожидаемое значение в Википедии
• Имею ввиду в Википедии
• Дисперсия в Википедии
• Стандартное отклонение в Википедии
• Ковариантность в Википедии
• Выборочное среднее и ковариация
• Коэффициент корреляции Пирсона
• Ковариационная матрица в Википедии
• Оценка ковариационных матриц в Википедии

Сообщений

• Что такое ковариационная матрица?, 2016
• Геометрическая интерпретация ковариационной матрицы 2014

Резюме

В этом уроке вы узнали, как работают фундаментальные статистические операции и как их реализовать, используя NumPy с обозначениями и терминологией из линейной алгебры.

В частности, вы узнали:

• Каковы ожидаемое значение, среднее значение и среднее значение и как рассчитать тогда.
• Что такое дисперсия и стандартное отклонение и как их рассчитать.
• Что такое ковариационная, корреляционная и ковариационная матрицы и как их вычислять.

У вас есть вопросы?
Задайте свои вопросы в комментариях ниже, и я сделаю все возможное, чтобы ответить.

3.3. Математические ожидания и ковариации векторов и матриц

При работе с линейными моделями удобно представлять данные в виде векторов или матриц. Элементы некоторых векторов или матриц статистических линейных моделей являются случайными переменными. Определение случайной переменной было дано. Значение этой переменной зависит от случайного результата опыта.

В этой книге рассматривается такой тип векторов случайных переменных отклика, элементы которого могут быть коррелированы, а влияющие на них переменные являются контролируемыми и неслучайными. В конкретной линейной модели, влияющие на отклик переменные, имеют выбранные или полученные в результате расчёта детерминированные значения. Таким образом, в рассматриваемых линейных моделях имеются два вектора случайных переменных:

у= и e=.

Значения i-й переменной у_i (i=1, 2, …, n) отклика наблюдаются в результате проведения i-го опыта эксперимента, а значения переменной e_i случайной ошибки не наблюдаются, но могут оцениваться по наблюдаемым значениям переменной отклика и значениям влияющих на неё переменных.

При рассмотрении линейных моделей широко используются векторы и матрицы случайных переменных, поэтому в первую очередь для них необходимо обобщить идеи математического ожидания, ковариации и дисперсии.

Математические ожидания

Математическое ожидание вектора у размеров пх1 случайных переменных y₁, y₂, …, у_п определяется как вектор их ожидаемых значений:

Е(у)=Е===y,                                        (3.3.1)

Рекомендуемые материалы

где E(у_i)=y_i получается в виде E(у_i)=, используя функцию f_i(у_i) плотности вероятности безусловного распределения переменной у_i.

Если х и у — векторы случайных переменных размеров пх1, то, в силу (3.3.1) и (3.2.7), математическое ожидание их суммы равно сумме их математических ожиданий:

Е(х+у)=Е(х)+Е(у).                                                    (3.3.2)

Пусть у_ij (i=1, 2, …, m; j=1, 2, …, п) набор случайных переменных с ожидаемыми значениями E(у_ij). Выражая случайные переменные и их математические ожидания в матричной форме, можно определить общий оператор математического ожидания матрицы Y=(y_ij) размеров mхп следующим образом:

Определение 3.3.1. Математическое ожидание матрицы Y случайных переменных равно матрице математических ожиданий её элементов

E(Y)=[E(y_ij)].

По аналогии с выражением (3.3.1), ожидаемые значения матрицы Y случайных переменных представляются в виде матрицы ожидаемых значений:

E(Y)==.     (3.3.3)

Вектор можно рассматривать как матрицу, следовательно, определение 3.3.1 и следующая теорема справедливы и для векторов.

Теорема 3.3.1. Если матрицы А=(а_ij) размеров lхm, B=(b_ij) размеров nхp, С=(c_ij) размеров lхp – все имеют элементами постоянные числовые значения, а Y – матрица размеров mхn случайных переменных, то

E(AYB+C)=AE(Y)B+C.                                         (3.3.4)

Доказательство дано в книгах [Себер (1980) стр.19; Seber, Lee (2003) стр.5]

□

Там же доказывается, что, если матрицы A и В размеров mхn, элементами которых являются постоянные числовые значения, а х и у — векторы случайных переменных размеров пх1, то

E(Aх+Bу)=AE(х)+BE(у).

Если f(Y) – линейная функция матрицы Y, то её ожидаемое значение находится по формуле Е[f(Y)]=f[Е(Y)] [Boik (2011) cтр.134]. Например, если матрицы А размеров рхm, B размеров пхр и С размеров рхр — все имеют элементами постоянные числовые значения, а матрица Y размеров тхп случайных переменных, то

E[след(AYB+C)]=след[E(AYB+C)], так как след матрицы — линейный оператор

=след[AE(Y)B+C], так как AYB+C — линейная функция матрицы Y

=след[AE(Y)B]+след(C).                                                                 (3.3.5)

Ковариации и дисперсии

Аналогичным образом можно обобщить понятия ковариации и дисперсии для векторов. Если векторы случайных переменных х размеров mх1 и у размеров nх1, то ковариация этих векторов определяется следующим образом.

Определение 3.3.2. Ковариацией векторов х и у случайных переменных является прямоугольная матрица ковариаций их элементов

C(х, у)=[C(х_i, у_j)].

Теорема 3.3.2. Если случайные векторы х и у имеют векторы математических ожиданий E(x)=x и Е(у)=y, то их ковариация

C(х, у)=E[(x–x)(y–y)^T].

Доказательство:

C(х, у)=[C(х_i, у_j)]

={E[(х_i–x_i)(y_j–y_j)]}               [в силу (3.2.9)]

=E[(x–x)(y–y)^T].      [по определению 3.3.1]

□

Применим эту теорему для нахождения матрицы ковариаций векторов х размеров 3х1 и у размеров 2х1

C(х, у)=E[(x–x)(y–y)^T]

=E

=Е

=.

Определение 3.3.3. Если х=у, то матрица ковариаций C(у, у) записывается в виде D(у)=E[(y–y)(y–y)^T] и называется матрицей дисперсий и ковариаций вектора у. Таким образом,

D(у)=E[(y–y)(y–y)^T]=[C(у_i, у_j)]

=.                (3.3.4)

А так как C(у_i, у_j)=C(у_j, у_i), то матрица (3.3.4) симметричная и квадратная.

Матрица дисперсий и ковариаций вектора у представляется в виде ожидаемого значения произведения (y–y)(y–y)^T. В силу (П.2.13), произведение (y_i–y_i)(y_j–y_j) является (ij)-м элементом матрицы (y–y)(y–y)^T. Таким образом, в силу (3.2.9) и (3.3.4), математическое ожидание E[(y_i–y_i)(y_j–y_j)]=s_ij является (ij)-м элементом Е[(y–y)(y–y)^T]. Отсюда

E[(y–y)(y–y)^T]=.                  (3.3.5)

Дисперсии s₁₁, s₂₂, …, s_пп переменных y₁, y₂, …, у_п и их ковариации s_ij, для всех i≠j, могут быть удобно представлены матрицей дисперсий и ковариаций, которая иногда называется ковариационной матрицей и обозначается прописной буквой S строчной s:

S=D(у)=                                (3.3.6)

В матрице S i-я строка содержит дисперсию переменной у_i и её ковариации с каждой из остальных переменных вектора у. Чтобы быть последовательными с обозначением s_ij, используем для дисперсий s_ii=s_i², где i =1, 2, …, n. При этом дисперсии расположены по диагонали матрицы S и ковариации занимают позиции за пределами диагонали. Отметим различие в значении между обозначениями D(у)=S для вектора и С(у_i, у_j)=s_ij для двух переменных.

Матрица S дисперсий и ковариаций симметричная, так как s_ij=s_ji [см. (3.2.9)]. Во многих приложениях полагается, что матрица S положительно определённая. Это обычно верно, если рассматриваются непрерывные случайные переменные, и между ними нет линейных зависимостей. Если между переменными есть линейные зависимости, то матрица S будет неотрицательно определённой.

Для примера найдём матрицу дисперсий и ковариаций вектора у размеров 3х1

D(у)=E[(y–y)(y–y)^T]

=E

=E

=.

=.

Как следует из определения 3.3.3,

D(у)=E[(у–y)(y–y)^T],                                              (3.3.7)

что после подобного сделанному в (3.2.4) преобразованию приводится к выражению

D(y)=E(yy^T)–yy^T.                                                    (3.3.8)

Последние два выражения являются естественным обобщением одномерных результатов данных выражениями (3.2.2) и (3.2.4).

Пример 3.3.1. Если а — какой-либо вектор числовых значений тех же размеров пх1, что и вектор у, то

D(y–а)=D(y).

Это следует из того, что y_i–a_i–E(y_i–a_i)=y_i–a_i–E(y_i)+a_i=y_i–E(y_i), так что

C(y_i–a_i, y_j–a_j)=C(y_i, y_j).

□

Напомним, что симметричная матрица А является положительно определенной, если для всех векторов у≠0 квадратичная форма у^ТАу>0. В дальнейшем будет использоваться часто следующая теорема.

Теорема 3.3.3. Если у — вектор случайных переменных, в котором ни одна из переменных не является линейной комбинации остальных, то есть, нет вектора а≠0 и числа b таких, что а^Ту=b для любого у, то D(у)=S — положительно определенная матрица.

Доказательство этой теоремы дано в [Себер (1980) стр.22].

□

Обобщенная дисперсия и нормированный вектор

Матрица S содержит дисперсии и ковариации всех п случайных переменных вектора у и всесторонне представляет полную их вариацию. Обобщённой мерой, характеризующей вариацию случайных переменных вектора у, может служить определитель матрицы S:

Обобщенная дисперсия =det(S).                                       (3.3.9)

В качестве статистики обобщённой дисперсии используется обобщённая выборочная дисперсия, определяемая детерминантом матрицы S=Y^T(I–Е/n)Y/(n–1) вариаций и ковариаций выборочных значений переменных вектора у, представленных матрицей Y=[y₁, y₂, …, y_k], где её столбцы составлены из векторов значений переменных вектора у [Rencher, Christensen (2012) стр.81]:

Обобщенная выборочная дисперсия =det(S).                  (3.3.10)

Если det(S) малый, то значения переменных вектора у располагаются ближе к их усреднённым значениям вектора , чем, если бы det(S) был большим. Малое значение det(S) может указывать также на то, что переменные y₁, y₂,…, у_п вектора у сильно взаимно коррелированы и стремятся занимать подпространство меньшее, чем п измерений, что соответствует одному или большему числу малых собственных значений [Rencher (1998) раздел 2.1.3; Rencher, Christensen (2012) стр.81].

Для получения полезной меры разности между векторами у и y необходимо учитывать дисперсии и ковариации переменных вектора у. Как для одной нормированной случайной переменной, получаемой по формуле z=(у–y)/s и имеющей среднее равное 0 и дисперсию равную 1, нормированная разность между векторами у и y определяется в виде

Нормированная разность =(у–y)^ТS^–1(у–y).                     (3.3.11)

Использование матрицы S^–1 в этом выражении нормирует (трансформирует) переменные вектора у так, что нормированные переменные имеют средние равные 0 и дисперсии равные 1, а также становятся и некоррелированными. Это получается потому, что матрица S положительно определённая. По теореме П.6.5 её обратная матрица тоже положительно определённая. В силу (П.12.18), матрица S^–1=S^–1/2S^–1/2. Отсюда

(у–y)^ТS^–1(у–y)=(у–y)^ТS^–1/2S^–1/2(у–y)

=[S^–1/2(у–y)]^Т[S^–1/2(у–y)]

=z^Тz,

Вам также может быть полезна лекция «Построение формы в ранне многоголосии».

где z=S^–1/2(у–y) — вектор нормированных случайных переменных. Математическое ожидание вектора z получается

Е(z)=Е[S^–1/2(у–y)]=S^–1/2[Е(у)–y]=0

и его дисперсия

D(z)=D[S^–1/2(у–y)]=S^–1/2D(у–y)S^–1/2=S^–1/2SS^–1/2=S^–1/2S^1/2S^1/2S^–1/2=I.

Следовательно, по пункту 2 теоремы 4.5.2 следующей главы вектор S^–1/2(у–y) имеет нормальное распределение N(0, I).

Для нормированной разности, как параметра, есть соответствующая статистика, а именно, выборочная нормированная дистанция, определяемая формулой (у–)^ТS^–1(у–) и называемая часто дистанцией Махаланобиса [Mahalanobis (1936); Seber (2008) cтр.463]. Некоторый п-мерный гиперэллипсоид (у–)^ТS^–1(у–)=а², центрированный вектором  и базирующийся на S^–1 для нормирования расстояния до центра, содержит выборочные значения переменных вектора у. Гиперэллипсоид (у–)^ТS^–1(у–) имеет оси пропорциональные квадратным корням собственных значений матрицы S. Можно показать, что объём гиперэллипсоида пропорционален [det(S)]^1/2. Если минимальное собственное значение матрицы S равно нулю, то в этом направлении нет оси и гиперэллипсоид расположен в (п–1)-мерном подпространстве п-мерного пространства. Следовательно, его объём в п-мерном пространстве равен 0. Нулевое собственное значение указывает на избыточность переменных вектора у. Для устранения этого необходимо убрать одну или более переменных, являющихся линейными комбинациями остальных.