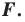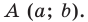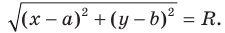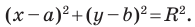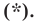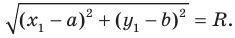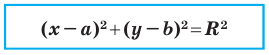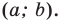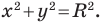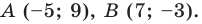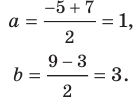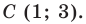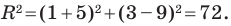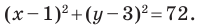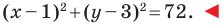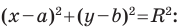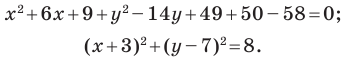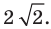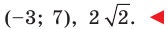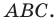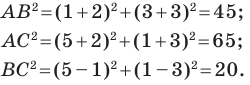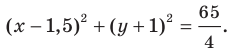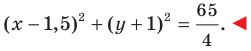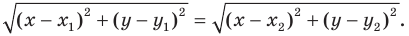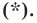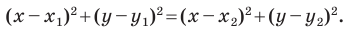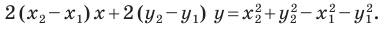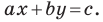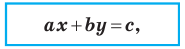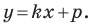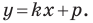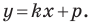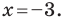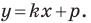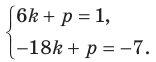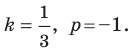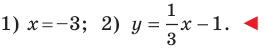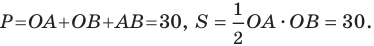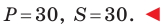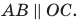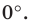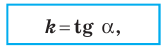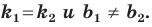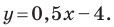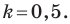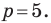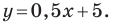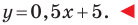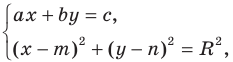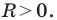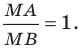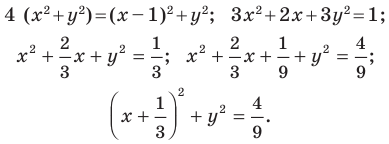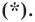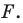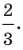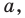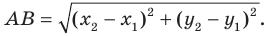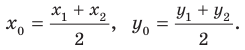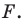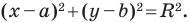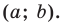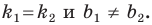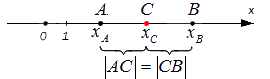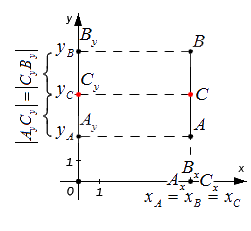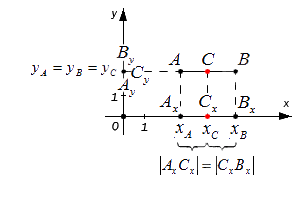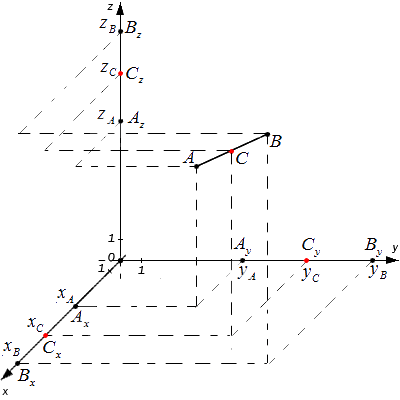Что такое отрезок
Чтобы изучить эту тему досконально, давайте начнем с самого простого: с определения отрезка.
Отрезок — это прямая, у которой есть начало и конец, или же прямая, которая соединяет две произвольные точки, не совпадающие друг с другом.
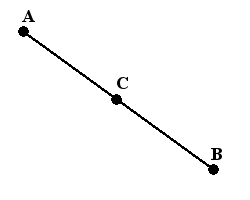
Отрезок называют заглавными буквами латинского алфавита по названию конечных точек. Причем можно расставлять буквы в любом порядке: АВ и ВА — равноценные варианты. Рассмотрите иллюстрацию, посчитайте и назовите все отрезки.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Что такое середина отрезка
Середина отрезка — это точка, которая находится на равном расстоянии от его концов. Иначе можно сказать так: это точка, которая делит отрезок пополам.
Так, на рисунке ниже D — середина отрезка СК, так как СD = DK. Обратите внимание, как на чертеже обозначаются равные по длине отрезки — мы ставим на них равное количество черточек.
Главный вопрос, который нас сегодня интересует, это координаты середины отрезка.
Координаты — это положение точки в пространстве.
Мы можем рассмотреть отрезок, который лежит на координатной прямой, тогда координата будет одна. В Декартовой системе координат оХУ будет две координаты, причем вначале записывают х, потом у. Например: С (5; 3): К (4; 8). Еще мы можем поместить отрезок в трехмерное пространство, тогда у каждой точки будет три координаты: х, у, z.
Кажется, что чем дальше, тем сложнее, но на самом деле это не совсем так. Хорошая новость: в каждом из случаев мы будем использовать один и тот же принцип, так что вы обязательно во всем разберетесь!
Как найти координаты середины отрезка на координатной прямой
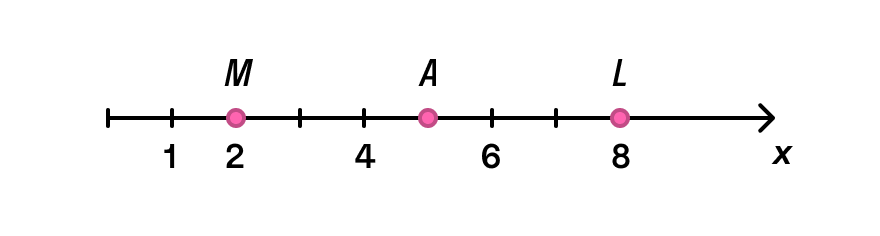
Изобразим горизонтальную координатную прямую оХ и отметим на ней две точки: М и L. Координату точки М запишем как Хм, точки L — соответственно XL. Поставим лежащую на отрезке точку А — середину ML, MA = LA.
Определим координаты точек: Хм = {2}, XL = {8}. Чтобы найти середину отрезка, воспользуемся формулой XA=(XM+XL)/2 и получим:
ХА = (2 + 8)/2 = 5.
Проверим, верна ли формула. Для этого определим координаты середины отрезка графическим методом.Действительно: фактическая координата точки А совпадает со значением, которое мы получили.
Подумайте, взяли ли мы эту формулу случайно или же ее можно вывести. Да, конечно, второй вариант верный — в математике не используют ничего непроверенного. Давайте посмотрим, каким образом можно доказать истинность формулы, тем более, что мы возьмем ее за основу при решении более сложных задач.
-
Точка А — это середина отрезка, а значит, MA = LA.
-
Расстояние между точками можно рассчитать через разность модулей их координат: │ХА – ХМ│=│ХL – ХА│.
-
Преобразуем правую часть, вынесем знак минуса: ХА – ХМ= — (ХА –ХL).
-
Перенесем ХА в левую часть, а все остальное — в правую: 2ХА= ХL+ ХМ.
-
Найдем ХА: ХА = (ХL + ХМ)/2.
Вот мы и вывели формулу координат середины отрезков! Чтобы лучше закрепить материал, сделаем пару заданий.
Задача 1
Определите координаты середины отрезка АВ, если ХА = –2, ХB = 10.
Решение
Обозначим точку середины отрезка буквой Т. Тогда Хт = (ХА + ХB)/2 = (–2 + 10)/2 = 4.
Ответ: Хк = {4}.
Задача 2
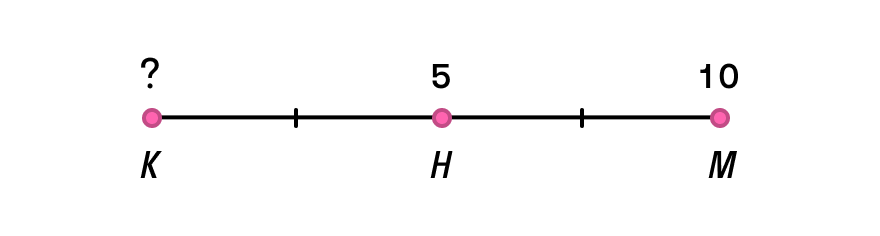
Определите координаты начала отрезка КМ с серединой в точке Н, если Хм = 5, Хн = 10.
Решение
Вначале запишем формулу для середины отрезка: Хн = (Хк + Хм)/2. Выразим Хк через нее:
Хн = (Хк + Хм)/2,
2Хн = (Хк + Хм),
2Хн – Хм = Хк,
Хк = 2Хн – Хм = 2 * 5 – 10 = 0.
Ответ: Хк = {0}
Как найти середину отрезка на плоскости
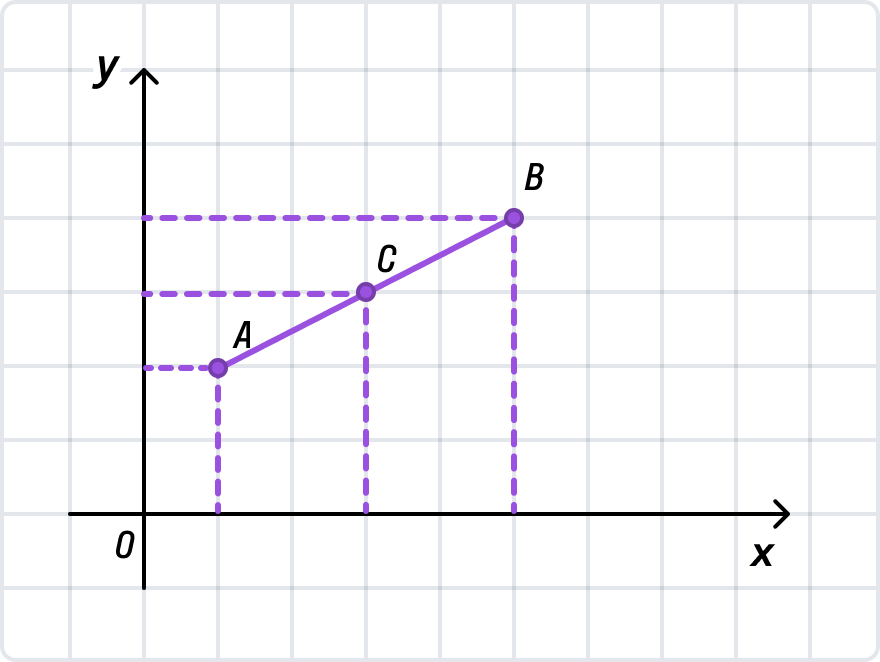
В Декартовой системе координат у каждой точки есть две координаты: по оси оХ и оУ. Изобразим отрезок АВ с координатами А (1; 3), В (3; 6) и точкой С — серединой отрезка.
Чтобы найти координаты точки С, мы воспользуемся уже известной нам формулой, но применим ее к каждой координате в отдельности. Вначале рассчитаем Хс:
Хс = (ХА + ХB)/2 = (1 + 3)/2 = 2.
Тогда УC = (УA + УB)/2 = (3 + 6)/2 = 4,5. Значит С (2; 4,5).
Не пугайтесь, если отрезок на чертеже параллелен оси оХ или оУ: мы четко идем по нашему алгоритму и ничего не меняем.
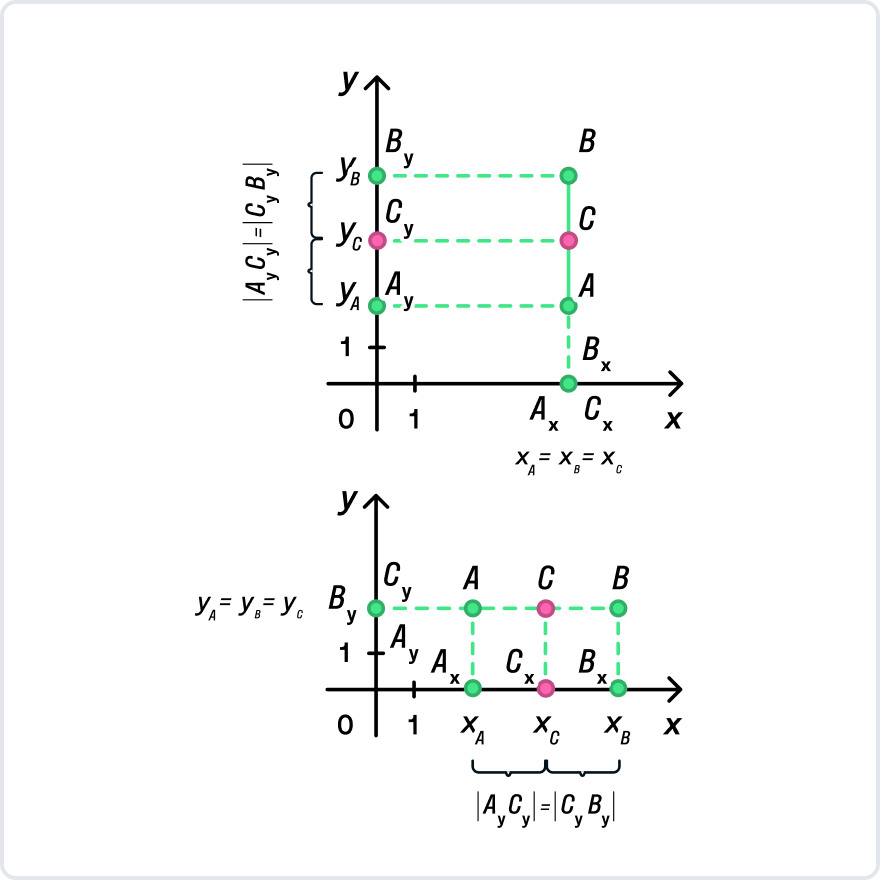
Важно заметить: если отрезок параллелен оси оУ, координаты концов и середины отрезка по оХ будут совпадать, ХА = ХС = ХВ. Если же отрезок параллелен оси оХ, совпадут координаты по оУ: УА = УВ = УС.
И вновь пришло время задачек. Давайте разберем несколько примеров решения.
Задача 3
В системе координат находятся две точки: С (–6; 4) и К (2; 8). Определите координаты середины отрезка.
Решение
Обозначим середину отрезка точкой О. Тогда:
ХО = (ХС + ХК)/2 = (–6 + 2)/2 = –2,
УО = (УС + УК)/2 = (4 + 8)/2 = 6.
Ответ: О (-2; 6).
Задача 4
Дан треугольник с вершинами АВС: А (-2; 4), В (4; 6), С (3; -5). Определите координаты точки М — медианы ВМ.
Решение
Медиана — отрезок, который проведен из вершины треугольника и делит противоположную сторону пополам. А значит, медиана ВМ делит на равные части сторону АС, АМ = МС. Тогда:
ХМ = (ХА + ХС)/2 = (–2 + 3)/2 = 0,5,
УМ = (УА + УС)/2 = (4 – 5)/2 = –0,5.
Ответ: М (0,5; –0,5).
Координаты середины отрезка в пространстве
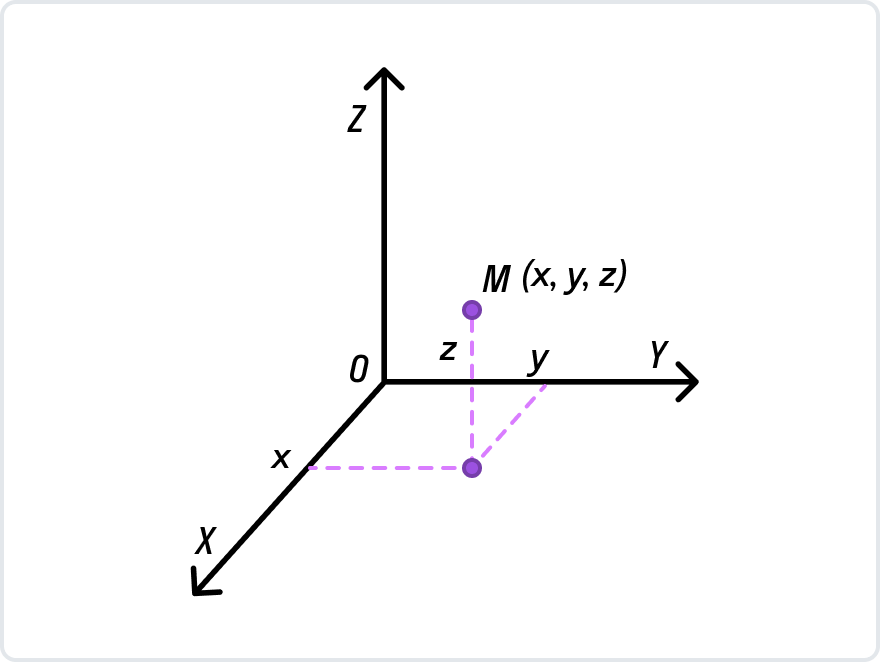
Вспомните, чем пространство отличается от плоскости. Правильно, третьим измерением! В том смысле, что добавляется еще одна координатная ось: оZ. Как это выглядит, можно посмотреть на рисунке ниже.
При этом формула нахождения середины отрезка остается неизменной. Если мы изобразим в трехмерном пространстве отрезок АВ с серединой в точке С, тогда:
ХС = (ХА + ХВ)/2,
УС = (УА + УВ)/2,
ZС = (ZА + ZВ)/2.
Координаты середины отрезка через радиус-векторы его концов
По сути, этот способ нельзя назвать каким-то новым и уникальным. Он лишь еще раз доказывает истинность формулы координат середины отрезков, только через алгебру. Чтобы разобраться в нем, давайте сначала вспомним определение вектора.
Вектор — это направленный отрезок прямой, то есть отрезок, для которого указано, какая из его граничных точек является началом, а какая — концом.
Векторы — достаточно обширная тема. Чтобы разобраться в ней, не хватит и двух статей. Но сейчас мы с вами будем использовать всего несколько тезисов, которые помогут разобраться в теме.
-
Векторы можно изображать в системах координат оХУ и оХYZ, т. е. в двумерной и трехмерной.
-
Координаты начала и конца векторов записывают так же, как и для отрезков: (x; y) и (x; y; z).
-
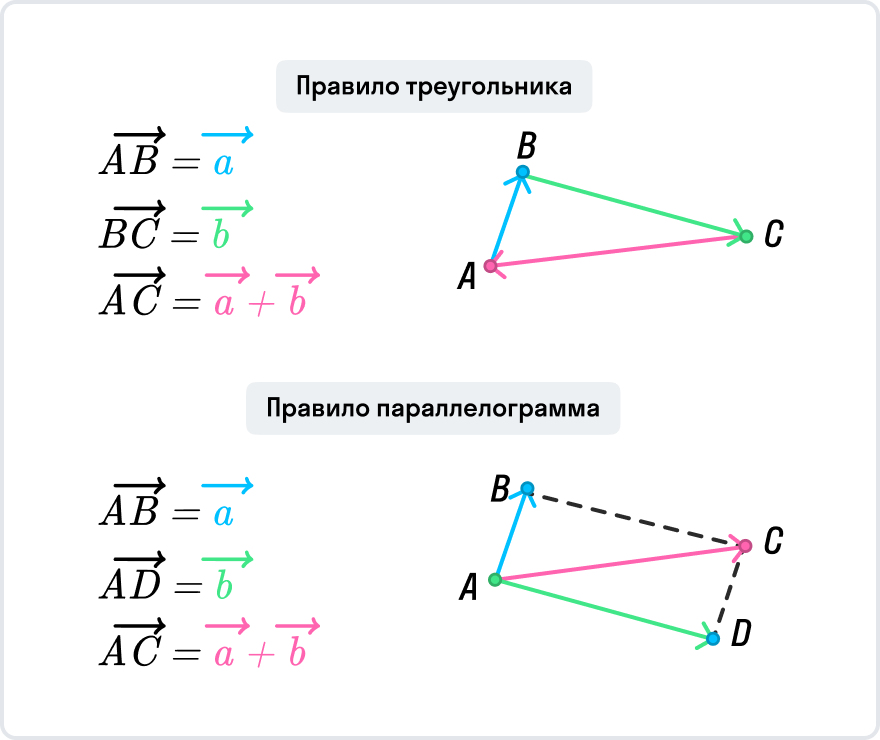
Сумму векторов можно найти по методу треугольника или параллелограмма. Картинка ниже поможет вам вспомнить, как ими пользоваться.
Радиус-вектор — вектор, который задает положение точки в пространстве относительно некоторой заранее фиксированной точки — начала координат.
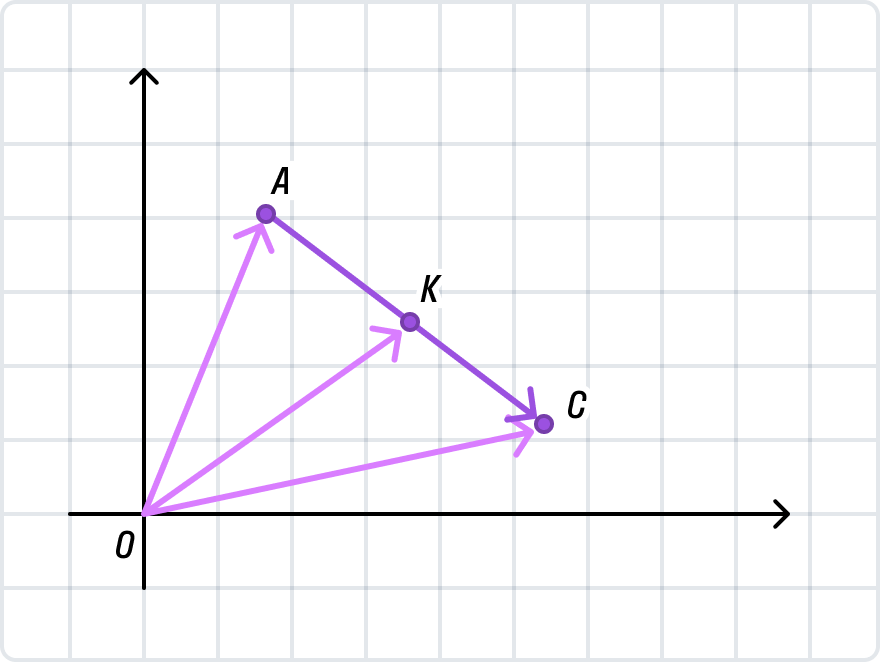
Давайте разберемся, как доказать формулу для нахождения координаты середины отрезка через радиус-векторы его концов. В Декартовой системе координат нарисуем вектор
с серединой в точке К. Координаты точки А (ХА; УА; ZА), К (ХК; УК; ZК), С (ХС; УС; ZС).Проведем радиус-векторы
,
,
.
Согласно определению середины отрезка: ОК = ½(ОС + ОА). Координаты векторов ОА, ОК, ОС соответственно равны координатам точек А, К, С, так как координаты точки О (0; 0; 0).
ОА (ХА – 0, УА – 0, ZА – 0) = (ХА; УА; ZА),
ОК (ХК – 0, УК – 0, ZК – 0) = (ХК; УК; ZК,),
ОС (ХС– 0, УС – 0, ZС – 0) = (ХС; УС; ZС).
Тогда запишем равенство ОК = ½(ОС + ОА) через координаты:
ХК = 1/2(ХА + ХО),
УК = 1/2(УА + УО),
ZК = 1/2(ZА + ZО).
Напоследок мы сделаем небольшой перерыв, забудем про формулы и числа. Давайте подумаем, как можно найти середину отрезка, если мы не знаем координат его концов.
Например, нарисуем отрезок на песчаном пляже во время каникул. Определить точные координаты в таком случае будет достаточно сложно, правда? Вряд ли вы взяли с собой в отпуск набор линеек, чтобы вычислить длину отрезка. С подобным заданием вы могли столкнуться и на уроках геометрии, где учитель раздавал вам чистые нелинованные листы бумаги и просил найти середину отрезка без использования линейки.
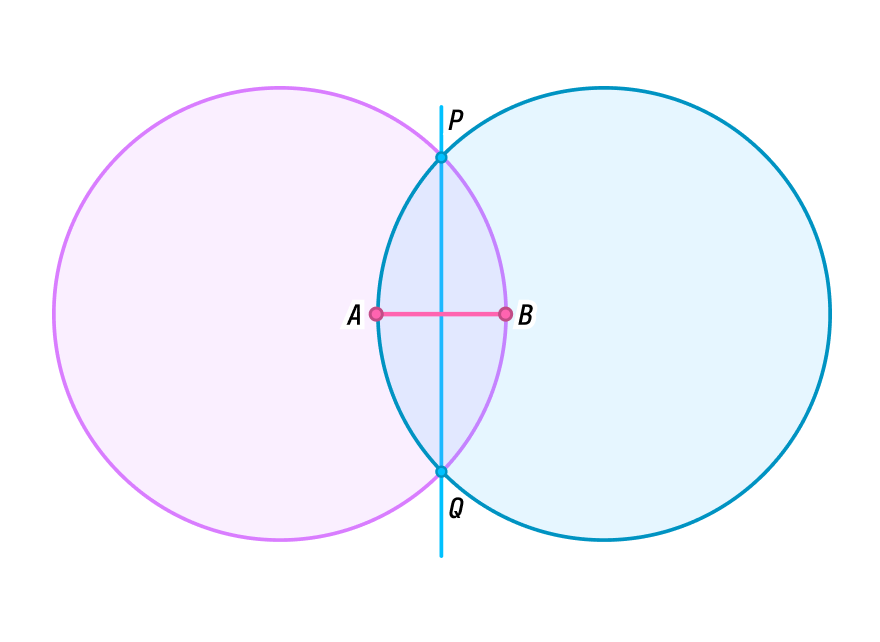
Сейчас мы обучим вас волшебному методу, приготовьтесь! Все что вам понадобится — это циркуль. Нарисуем на бумаге отрезок АВ любой длины. Поставим иголку циркуля в точку А и начертим окружность с радиусом, равным АВ. Далее повторим действие — прочертим такую же окружность с центром в точке В.
Мы видим, что окружности пересеклись дважды: снизу и сверху. Если соединить эти две точки, эта прямая пересечет наш исходный отрезок ровно в его середине.
Скептики вспомнят наш пример с пляжем и скажут: «Линейку мы с собой в отпуск не берем, но и циркуль ведь тоже! Что вы скажете на это?» А ответим мы вот что: приходите на курсы по профильной математики в Skysmart! Там вы научитесь не только заменять настоящий циркуль на самодельный, но еще подготовитесь к экзаменам, разовьете логику и узнаете много всего интересного. Ждем вас на занятиях!
Содержание:
Декартовы координаты на плоскости:
Изучая материал этой лекции, вы расширите свои знания о координатной плоскости.
Вы научитесь находить длину отрезка и координаты его середины, зная координаты его концов.
Сформируете представление об уравнении фигуры, выведете уравнения прямой и окружности.
Ознакомитесь с методом координат, позволяющим решать геометрические задачи средствами алгебры.
Расстояние между двумя точками с заданными координатами. Координаты середины отрезка
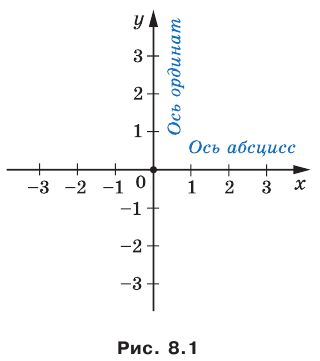
В 6 классе вы ознакомились с координатной плоскостью, то есть с плоскостью, на которой изображены две перпендикулярные координатные прямые (ось абсцисс и ось ординат) с общим началом отсчета (рис. 8.1). Вы умеете отмечать на ней точки по их координатам и наоборот, находить координаты точки, отмеченной на координатной плоскости.
Договорились координатную плоскость с осью
Координаты точки на плоскости 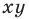
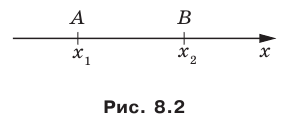
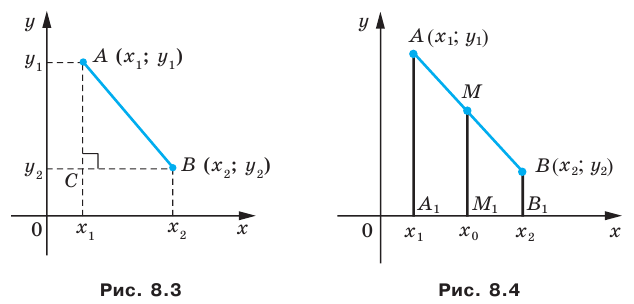
Вы знаете, как находить расстояние в между двумя точками, заданными своими координатами на координатной прямой. Для точек 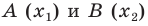
Научимся находить расстояние между точками 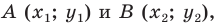
Рассмотрим случай, когда отрезок 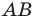
Через точки 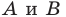
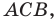
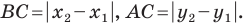
Тогда формулу расстояния между точками 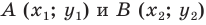
Докажите самостоятельно, что эта формула остается верной и для случая, когда отрезок 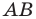
Пусть 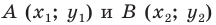
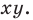
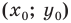
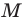
Рассмотрим случай, когда отрезок 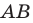
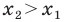
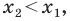
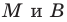
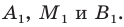
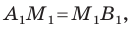
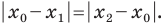
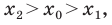
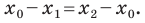

Формулы для нахождения координат середины отрезка остаются верными и для случая, когда отрезок 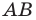
Пример №1
Докажите, что треугольник с вершинами в точках 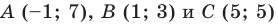
Решение:
Используя формулу расстояния между двумя точками, найдем стороны данного треугольника:
Следовательно, 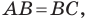
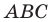
Поскольку 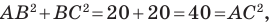
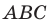
Пример №2
Точка 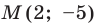
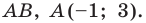
Решение:
Обозначим 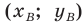
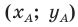
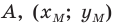
Поскольку 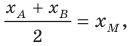
Аналогично
Ответ:
Пример №3
Докажите, что четырехугольник 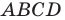
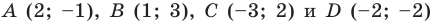
Решение:
Пусть точка 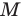
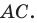
Следовательно,
Пусть точка 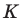
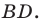
Следовательно,
Таким образом, точки 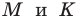
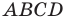
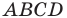
Найдем диагонали параллелограмма:
Следовательно, диагонали параллелограмма 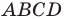
Уравнение фигуры. Уравнение окружности
Из курса алгебры 7 класса вы знаете, какую фигуру называют графиком уравнения. В этом пункте вы ознакомитесь с понятием уравнения фигуры.
Координаты 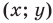
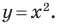
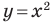
Определение. Уравнением фигуры 
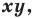
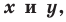
- если точка принадлежит фигуре
то ее координаты являются решением данного уравнения;
- любое решение
данного уравнения является координатами точки, принадлежащей фигуре
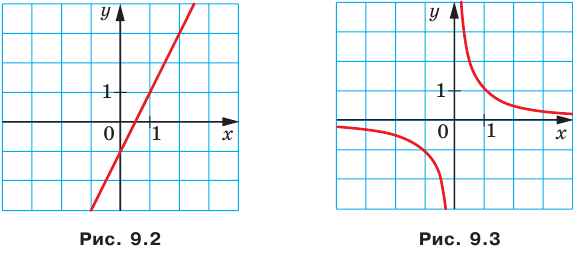
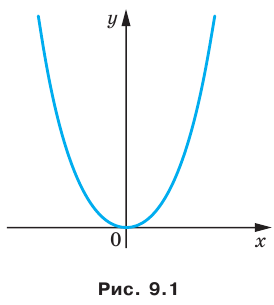
Например, уравнение прямой, изображенной на рисунке 9.2, имеет вид 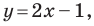
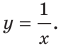
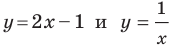
Если данное уравнение является уравнением фигуры 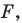
Пользуясь этими соображениями, выведем уравнение окружности радиуса 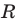
Пусть 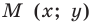
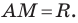
Отсюда
Мы показали, что координаты 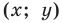
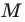
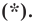
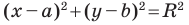
Пусть пара чисел 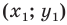
Тогда 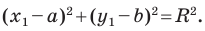
Это равенство показывает, что точка 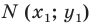
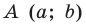
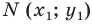
Итак, мы доказали следующую теорему.
Теорема 9.1. Уравнение окружности радиуса 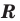
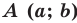
Верно и такое утверждение: любое уравнение вида 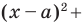
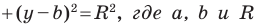
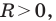
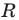
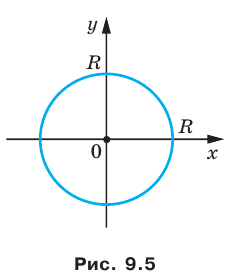
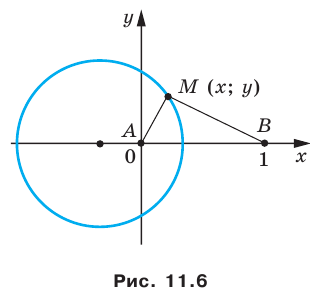
Если центром окружности является начало координат (рис. 9.5), то 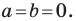
Пример №4
Составьте уравнение окружности, диаметром которой является отрезок 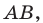
Решение:
Поскольку центр окружности является серединой диаметра, то можем найти координаты 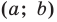
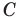
Следовательно,
Радиус окружности 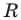
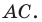
Следовательно, искомое уравнение имеет вид
Ответ:
Пример №5
Докажите, что уравнение 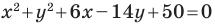
Решение:
Представим данное уравнение в виде
Следовательно, данное уравнение является уравнением окружности с центром в точке 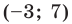
Ответ:
Пример №6
Докажите, что треугольник с вершинами в точках 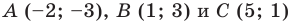
Решение:
Найдем квадраты сторон данного треугольника:
Поскольку 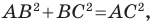
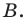
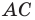
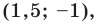
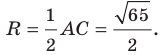
Ответ:
Уравнение прямой
В предыдущем пункте, рассматривая окружность как ГМТ, равноудаленных от данной точки, мы вывели ее уравнение. Для того чтобы вывести уравнение прямой, рассмотрим ее как ГМТ, равноудаленных от двух данных точек.
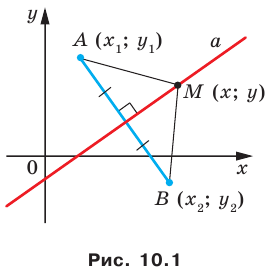
Пусть 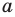
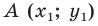
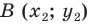
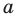
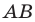
Пусть 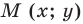
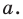
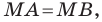
Мы показали, что координаты 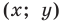
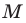
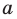
Теперь покажем, что любое решение уравнения 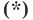
Пусть 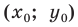
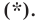
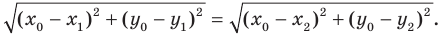
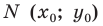
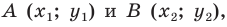
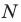
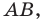
Итак, мы доказали, что уравнение 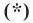
Однако из курса алгебры 7 класса вы знаете, что уравнение прямой выглядит гораздо проще, а именно: 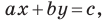
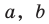
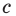
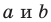
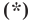
Раскроем скобки и приведем подобные слагаемые. Получим:
Обозначив 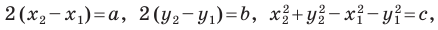
Поскольку точки 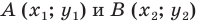
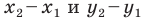
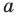
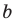
Итак, мы доказали следующую теорему.
Теорема 10.1. Уравнение прямой имеет вид?
где 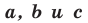
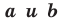
Верно и такое утверждение: любое уравнение вида 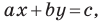
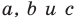
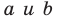
Если 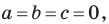
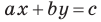
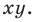
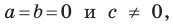
Из курса алгебры 7 класса вы знаете, что уравнение вида 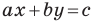
на уроках алгебры в 7 классе мы приняли без доказательства тот факт, что графиком линейной функции 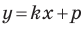
Перепишем уравнение 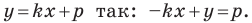
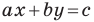
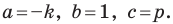
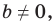
А любую ли прямую на плоскости можно задать уравнением вида 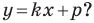
Дело в том, что прямая, перпендикулярная оси абсцисс, не может являться графиком функции, а следовательно, не может быть задана уравнением вида
Вместе с тем, если в уравнении прямой 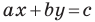
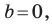
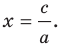
Если 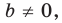
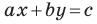
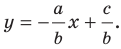
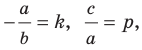
Следовательно, если 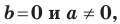
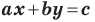
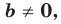
Уравнение невертикальной прямой удобно записывать в виде
Данная таблица подытоживает материал, рассмотренный в этом пункте.
Пример №7
Составьте уравнение прямой, проходящей через точки:
Решение:
1) Поскольку данные точки имеют равные абсциссы, то прямая 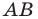
2) Поскольку данные точки имеют разные абсциссы, то прямая 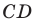
Подставив координаты точек 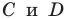
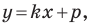
Решив эту систему уравнений, находим, что
Ответ:
Пример №8
Найдите периметр и площадь треугольника, ограниченного прямой 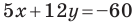
Решение:
Найдем точки пересечения данной прямой с осями координат.
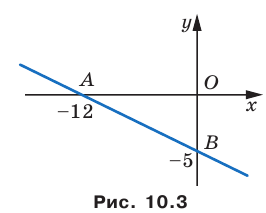
С осью абсцисс: при 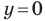
С осью ординат: при 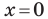
Следовательно, данная прямая и оси координат ограничивают прямоугольный треугольник 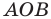
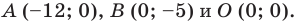
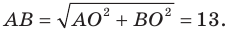
Ответ:
Угловой коэффициент прямой
Рассмотрим уравнение 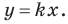
Покажем, что прямые 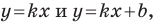
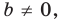
Точки 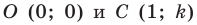
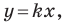
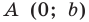
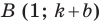
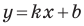
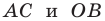
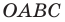
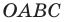
Теперь мы можем сделать такой вывод: если 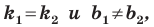
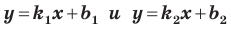
Пусть прямая 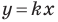
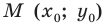
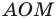
Если прямая 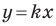
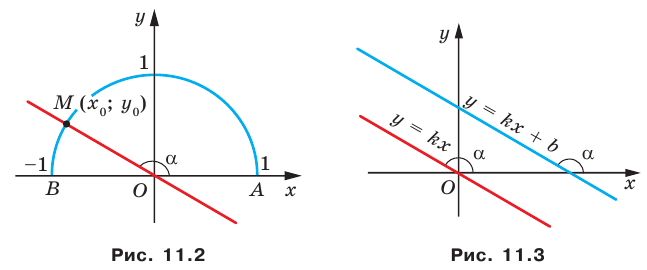
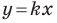
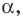
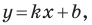
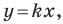
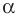
Рассмотрим прямую 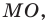
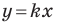
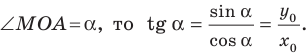
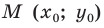
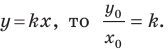
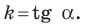
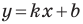
где 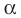
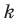
Если невертикальные прямые параллельны, то они образуют равные углы с положительным направлением оси абсцисс. Тогда тангенсы этих углов равны, следовательно, равны и их угловые коэффициенты. Таким образом,
если прямые 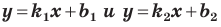
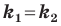
Выводы (1) и (2) объединим в одну теорему.
Теорема 11.1. Прямые 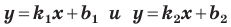
Пример №9
Составьте уравнение прямой, которая проходит через точку 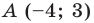
Решение:
Пусть уравнение искомой прямой 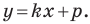
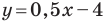
Следовательно, искомое уравнение имеет вид 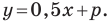
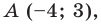
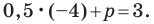
Искомое уравнение имеет вид
Ответ:
Метод координат
Мы часто говорим: прямая 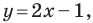
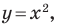
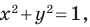
Проиллюстрируем сказанное на таком примере.
Из наглядных соображений очевидно, что прямая и окружность имеют не более двух общих точек. Однако это утверждение не является аксиомой, поэтому его надо доказывать.
Эта задача сводится к исследованию количества решений системы уравнений
где числа 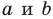
Решая эту систему методом подстановки, мы получим квадратное уравнение, которое может иметь два решения, одно решение или вообще не иметь решений. Следовательно, для данной системы существует три возможных случая:
- система имеет два решения — прямая и окружность пересекаются в двух точках;
- система имеет одно решение — прямая касается окружности;
- система не имеет решений — прямая и окружность не имеют общих точек.
С каждым из этих случаев вы встречались, решая задачи 10.17-10.19.
Метод координат особенно эффективен в тех случаях, когда требуется найти фигуру, все точки которой обладают некоторым свойством, то есть найти геометрическое место точек.
Отметим на плоскости две точки 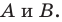
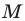
Это серединный перпендикуляр отрезка 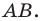
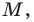
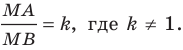
Плоскость, на которой отмечены точки 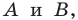
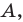
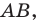
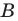
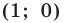
Пусть 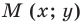
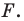
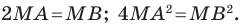
Следовательно, если точка 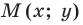
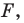
Пусть 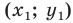
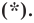
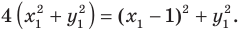
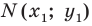
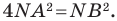
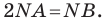
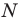
Таким образом, уравнением фигуры 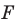
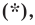
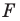
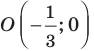
Мы решили задачу для частного случая, когда 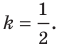
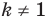
Как строили мост между геометрией и алгеброй
Идея координат зародилась очень давно. Ведь еще в старину люди изучали Землю, наблюдали звезды, а по результатам своих исследований составляли карты, схемы.
Во II в. до н. э. древнегреческий ученый Гиппарх впервые использовал идею координат для определения места расположения объектов на поверхности Земли.
Только в XIV в. французский ученый Николя Орем (ок. 1323-1382) впервые применил в математике идею Гиппарха: он разбил плоскость на клетки (как разбита страница вашей тетради) и стал задавать положение точек широтой и долготой.
Однако огромные возможности применения этой идеи были раскрыты лишь в XVII в. в работах выдающихся французских математиков Пьера Ферма и Рене Декарта. В своих трудах эти ученые показали, как благодаря системе координат можно переходить от точек к числам, от линий к уравнениям, от геометрии к алгебре.
Несмотря на то что П. Ферма опубликовал свою роботу на год раньше Р. Декарта, систему координат, которой мы сегодня пользуемся, называют декартовой. Р. Декарт в своей работе «Рассуждение о методе» предложил новую удобную буквенную символику, которой с незначительными изменениями мы пользуемся и сегодня. Вслед за Декартом мы обозначаем переменные последними буквами латинского алфавита 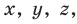
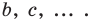
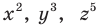
Справочный материал
Расстояние между двумя точками
Расстояние между точками 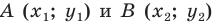
Координаты середины отрезка
Координаты 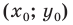
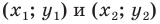
Уравнение фигуры
Уравнением фигуры 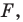
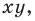
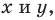
1) если точка принадлежит фигуре 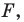
2) любое решение 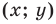
Уравнение окружности
Уравнение окружности радиуса 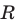
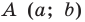
Любое уравнение вида 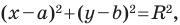
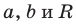
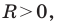
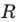
Уравнение прямой
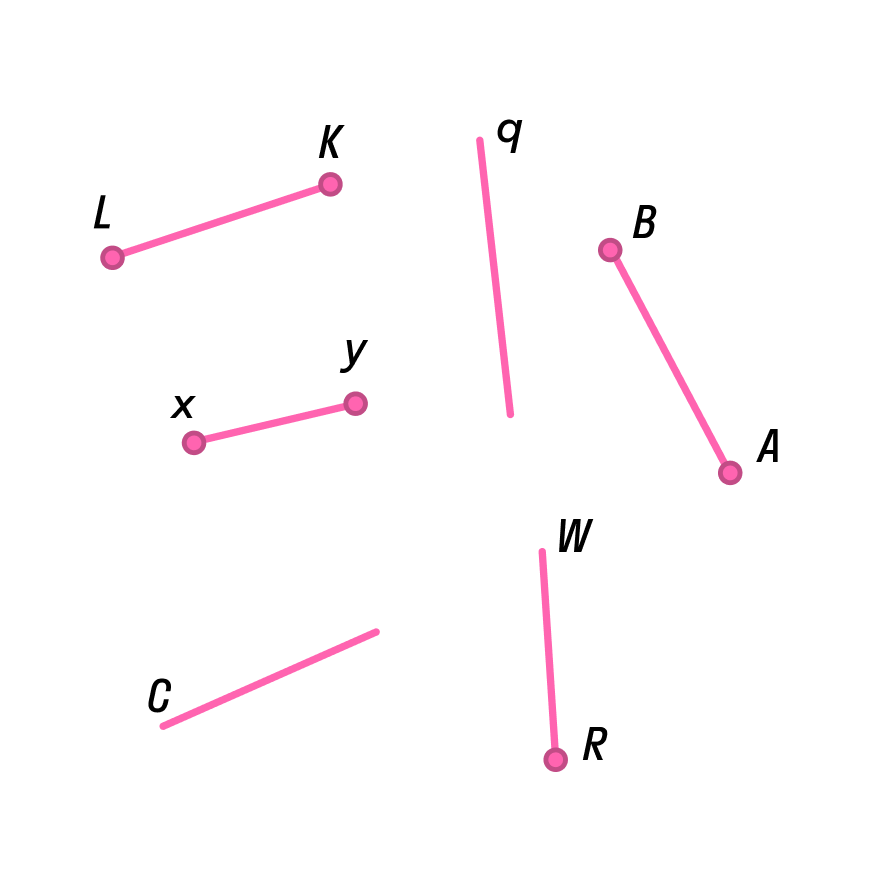
Уравнение прямой имеет вид 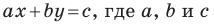
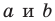
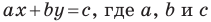
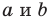
Если 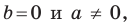
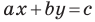
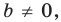
Угловой коэффициент прямой
Коэффициент 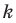
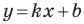
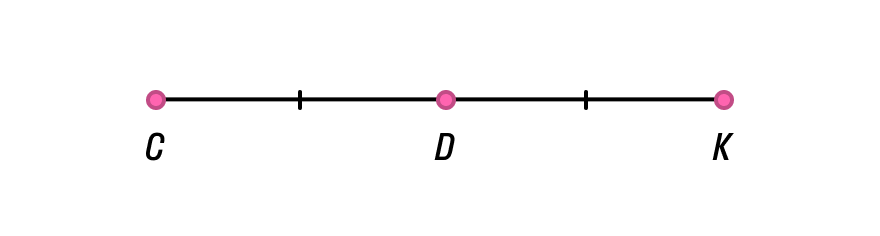
Необходимое и достаточное условие параллельности невертикальных прямых
Прямые 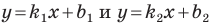
- Декартовы координаты в пространстве
- Геометрические преобразования в геометрии
- Планиметрия — формулы, определение и вычисление
- Стереометрия — формулы, определение и вычисление
- Перпендикулярность прямой и плоскости
- Взаимное расположение прямых в пространстве, прямой и плоскости
- Перпендикулярность прямых и плоскостей в пространстве
- Ортогональное проецирование
Определение.
Середина отрезка — это точка, которая лежит на отрезке и находится на равном расстоянии от конечных точек.
В геометрических задачах часто можно столкнуться с необходимостью найти середину отрезка заданного координатами точек его концов, например в задачах поиска медианы, средней линии, …
Каждая координата середины отрезка равна полусумме соответствующих координат концов отрезка.
Формулы вычисления расстояния между двумя точками:
- Формула вычисления координат середины отрезка с концами A(xa, ya) и B(xb, yb) на плоскости:
xc = xa + xb yc = ya + yb 2 2 - Формула вычисления координат середины отрезка с концами A(xa, ya, za) и B(xb, yb, zb) в пространстве:
xc = xa + xb yc = ya + yb zc = za + zb 2 2 2
Примеры задач на вычисление середины отрезка
Примеры вычисления координат середины отрезка на плоскости
Пример 1.
Найти координаты точки С, середины отрезка AB заданного точками A(-1, 3) и B(6, 5).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4).
Пример 2.
Найти координаты точки В, если известны координаты точки C(1; 5), середины отрезка AB и точки A(-1, 3).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
Ответ: B(3, 7).
Примеры вычисления координат середины отрезка в пространстве
Пример 3.
Найти координаты точки С середины отрезка AB заданного точками A(-1, 3, 1) и B(6, 5, -3).
Решение.
| xc = | xa + xb | = | -1 + 6 | = | 5 | = 2.5 |
| 2 | 2 | 2 |
| yc = | ya + yb | = | 3 + 5 | = | 8 | = 4 |
| 2 | 2 | 2 |
| zc = | za + zb | = | 1 + (-3) | = | -2 | = -1 |
| 2 | 2 | 2 |
Ответ: С(2.5, 4, -1).
Пример 4.
Найти координаты точки В если известны координаты точки C(1, 5, 2), середины отрезка AB и точки A(-1, 3, 10).
Решение.
xc =
xa + xb2
=> xb = 2xc — xa = 2·1-(-1)=2+1=3
yc =
ya + yb2
=> yb = 2yc — ya = 2·5-3=10-3=7
zc =
za + zb2
=> zb = 2zc — za = 2·2-10=4-10=-6
Ответ: B(3, 7, -6).
Любые нецензурные комментарии будут удалены, а их авторы занесены в черный список!
Основное определение отрезка
Определение
Отрезок — это прямая линия, которая соединяет две произвольно расположенные точки, именуемые окончанием отрезка. В качестве конкретного примера можно назвать точки A и B и соответственно отрезок AB.
Прямую АВ можно получить путем удлинения отрезка, который состоит из двух точек. Вследствие чего, можно сказать, что полученный отрезок АВ — это часть прямой, которая ограничена точками А и В. Отрезок объединяет обе точки, которые являются концами прямой, а также множество других точек, лежащих на отрезке.
Например: дана точка К которая расположена между заданными отметками, следовательно, можно сказать, что данная точка лежит на этом отрезке.
Определения
Длина прямой – конкретное отмеренное расстояние, которое задано в масштабе. Чаще всего данный параметр задается как АВ.
Середина отрезка – это некая определенная отметка, которая лежит на прямой и удалена от концов на одинаковом расстоянии друг от друга. Ее можно обозначить как координата С.
Середина отрезка на координатной прямой
Заданы следующие параметры: координатная прямая Ox; точки А и В, которые не совпадают с данной прямой.
Заданным точкам соответствуют действительные числовые значения [x_{A}] и [x_{B}]. Координата С — это середина отрезка А и В. Исходя из этого нужно определить значение координаты [x_{C}] .
AB = |a — b|, где A и B — это произвольные точки, расстояние между которыми надо найти, то есть, найти длину отрезка AB, a и b — координаты точек.
Выражение |a — b| можно заменить выражением |b — a|, так как a — b и b — a являются противоположными числами и их модули равны.
Следовательно, чтобы найти расстояние между точками координатной прямой надо из координаты одной точки вычесть координату другой точки.
Середина отрезка на плоскости
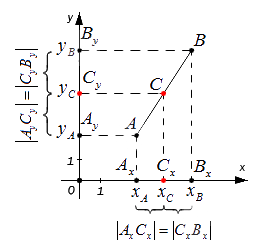
Зададим следующие параметры: прямоугольная система координат относительно заданной плоскости Oxy; две произвольно расположенные несовпадающие точки, для которых заданы координаты [mathrm{A}left(x_{A} y_{A}right)] и [Bleft(chi_{B} chi_{B}right)]. Точка C — это заданная середина отрезка АВ. Нужно вычислить координаты [x_{C}] и [y_{C}] относительно точки С.
Чтобы правильно проанализировать задачу, возьмем случай, когда точки A и В между собой не совпадают и расположены на одной координатной плоскости.
В свою очередь координатная плоскость является перпендикулярной относительной одной из осей.
Координаты отметок [A_{x} A_{y} B_{x} B_{y} C_{x} C_{y}] — это проекции точек А, В, С.
Согласно построению, все прямые можно назвать параллельными; прямые также параллельны между собой. Принимая во внимание данное свойство и теорему Фалеса из равенства А С = С В следуют, что все равенства между собой равны. Также они в свою очередь свидетельствуют о том, что точка [C_{x}] – это середина отрезка [A_{x}] и [B_{x}], [C_{y}] а – середина отрезка [A_{y}] и [B_{y}].
Опираясь на полученное выражение получаем основное уравнение середины отрезка на координатной плоскости.
[x_{c}=frac{x_{A}+x_{B}}{2}text { и } y_{c}=frac{y_{A}+y_{B}}{2}]
Данным набором формул можно использовать, когда точки А и B лежат на одной координатной плоскости или прямой. Которая соответственно перпендикулярна относительной одной из осей.
В данном случае координаты отрезка будут определяться по следующей формуле:
[x_{C}=frac{x_{A}+x_{B}}{2} text{ и } y_{c}=frac{y_{A}+y_{B}}{2}]
Параметры середины отрезка в пространстве
Для выведения основной формулы для решения подобного рода задач, нужно рассмотреть конкретный пример.
Дана система координат, две произвольные координатные точки с конкретными координатами [mathrm{A}left(A_{x} A_{y} A_{z}right)] и [mathrm{B}left(B_{chi} B_{y} B_{z}right)]. Нужно определить отметку точки C, которая в свою очередь будет являться серединой отрезка.
Согласно основной теоремы Фалеса, все равенства между собой являются равными. Следовательно, значение точек С будут являться серединами отрезков, каждой координатной плоскости, коих имеется три.
Можно составить и записать окончательную формулу для определения середины прямой при координатной плоскости, состоящей более чем двух осей.
[x_{c}=frac{x_{A}+x_{B}}{2} text{ и } y_{C}=frac{y_{A}+y_{B}}{2}, z_{c}=frac{z_{A}+z_{B}}{2}]
Данные формулы также можно применять в случаях, когда точки A и B расположены на одной из координатных прямых. Либо на прямой, которая перпендикулярна относительно одной из осей. Есть еще случай, когда точки расположены в одной координатной плоскости, которая перпендикулярна одной из координатных плоскостей.
Нет времени решать самому?
Наши эксперты помогут!
Определение координат середины отрезка через координаты радиус-векторов его концов
Формулу для определения отметок середины отрезка, можно определить применяя алгебраическое правило решения векторных выражений.
Исходные данные: прямоугольная декартова система координат Oxy, точки с конкретно заданными координатами [mathrm{A}left(A_{x} A_{y}right)] и [text { B }left(B_{x} B_{y}right)].
Точка C – это середина отрезка с точками А и В.
Согласно геометрическому правилу и определению, действия над векторами будет выглядеть следующим образом:
[overline{O C}=frac{1}{2} cdot(overline{O A}+overline{O B}).]
Координата С в данной ситуации — это значение, в которой пересекаются диагонали геометрической фигуры параллелограмм. Данная фигура построена на основании следующих векторов [overline{O A}] и [overline{O B}], иными словами — это точка середины диагоналей.
Координатные показатели радиуса — это векторные показатели, которые равны координатам, тогда будут верны и равенства: [overline{O A}left(x_{A} y_{A}right)] и [overline{O B}left(x_{B} y_{B}right)].
Выполним следующие действия над векторными значениями и получим следующие формулы:
[overline{O C}=frac{1}{2} cdot(overline{O A}+overline{O B})=left(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}right).]
Следовательно, заданная координата С обладает данными:
[left(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}right).]
Аналогичным образом определяется нахождение координат середины заданного отрезка в пространстве.
[Cleft(frac{x_{A}+y_{B}}{2}, frac{y_{A}+y_{B}}{2}, frac{z_{A}+z_{B}}{2}right)]
Примеры решения задачи, при нахождении точки середины отрезка
Примеры
Пример №1:
Заданы координатные данные. Точка А с показателями (-7,3) и В (2,4).
Нужно определить точку с отметками, которая является серединой отрезка А и В.
Решение:
Середину отрезка можно обозначить любой точкой. В данном примере возьмем наименование точки — С.
Координатные значения ее будут вычисляться как половина суммы координат концов заданного отрезка с точками А
и В.
Составим и запишем следующие формулы:
[x_{C}=frac{x_{A}+x_{B}}{2}=frac{-7+2}{2}=-frac{5}{2}\y_{C}=frac{y_{A}+y_{B}}{2}=frac{3+4}{2}=frac{7}{2}]
Ответ: искомые координатные значения середины отрезка будут равны следующим данным:
[mathrm{AB}left(-frac{5}{2}, frac{7}{2}right)]
Пример №2:
Заданы координатные отметки геометрической фигуры треугольника: АВС А(-1,0), В (3,2), С (9,-8). По условию
необходимо вычислить длину медианы АМ.
Решение:
По условию задачи AM – медиана, следовательно, точка M будет являться точкой середины отрезка BC. В первую
очередь необходимо определить координаты середины отрезка BC, а именно: точки M.
[x_{M}=frac{x_{B}+x_{C}}{2}=frac{3+9}{2}=6\y_{M}=frac{y_{B}+y_{C}}{2}=frac{2+(-8)}{2}=-3]
Так как, нам известны координатные значения двух концов медианы, точки А и М. Можно воспользоваться формулой
определения расстояния между заданными значениями, и вычислить окончательное значение медианы.
[AM=sqrt{(6-(-1))^{2}+(-3+0)^{2}}=sqrt{58}]
Ответ: [sqrt{58}].
Координаты середины отрезка
Содержание:
- Что такое середина отрезка
-
Правила нахождения координат середины отрезка, формулы
- Середина отрезка на координатной прямой
- Середина отрезка на плоскости
- Середина отрезка в пространстве
- Метод с использованием координат радиус-векторов концов отрезка
- Примеры решения задач
Что такое середина отрезка
Отрезок — это геометрическая фигура, представляющая собой ограниченный с двух сторон участок прямой.
Пусть точки A и B не совпадают. Если провести через них прямую, то образуется отрезок AB или BA, который ограничен точками A и B. Данные точки являются концами отрезка.
Длина отрезка — это расстояние между двумя точками, ограничивающими данный отрезок. Длина отрезка AB обозначается как модуль данной геометрической фигуры, то есть |AB|.
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Серединой отрезка является такая точка C, принадлежащая отрезку AB, которая расположена в центре данного отрезка, то есть |AC|=|CB|.
Правила нахождения координат середины отрезка, формулы
Середина отрезка на координатной прямой
Предположим, что несовпадающие точки A и B лежат на координатной прямая Ох. Известно, что A и B соответствуют действительные числа xA и xB, а точка С делит AB пополам. Определите координату xC, соответствующую С.
Так как C — это середина AB, то справедливо следующее равенство:
(left|ACright|=left|CBright|)
Вычислим расстояние между A и C, а также между C и B. Для этого определим модуль разницы их координат. На математическом языке это будет иметь вид:
(left|ACright|=left|CBright|Leftrightarrowleft|x_C-x_Aright|=left|x_B-x_Cright|)
Опустим знак модуля и получим справедливость двух выражений:
(x_C-x_A=x_B-x_C)
(x_C-x_A=-left(x_B-x_Cright))
Исходя из первого равенства, получим формулу нахождения xC, согласно которой координата точки С равна половине суммы координат A и B:
(x_C=frac{x_A+x_B}2)
Следствием второго равенства будет следующее утверждение:
(x_A=x_B)
Это противоречит заданным условиям, следовательно, формула определения координат середины отрезка выглядит так:
(x_C=frac{x_A+x_B}2)
Середина отрезка на плоскости
В декартовой системе координат Oxy расположены две точки A(xA,yA) и B(xB,yB), которые не совпадают между собой. Точка C является центром AB. Необходимо произвести вычисление координат xC и yC, соответствующих С.
Пусть произвольные точки А и В лежат на одной координатной прямой, а также не принадлежат прямым, располагающимся перпендикулярно к оси абсцисс или ординат. Опустим от заданных точек A, B, C перпендикуляры на ось x на ось y. Полученные точки пересечения с осями координат Ax, Ay; Bx, By; Cx, Cy — это проекции исходных точек.
По построению прямые AAx, BBx, CCx относительно друг друга находятся параллельно. Прямые AAy, BBy, CCy не пересекаются, то есть являются параллельными. Согласно равенству AB=BC, далее применим теорему Фалеса и получим:
(A_xC_x=C_xB_x)
(A_yC_y=C_yB_y)
Это значит, что Cx и Cy являются серединами отрезков AxBx и AyBy соответственно. Теперь воспользуемся формулой определения координат середины отрезка на координатной прямой и получим:
(x_C=frac{x_A+x_B}2)
(y_C=frac{y_A+y_B}2)
Данные формулы подходят для вычисления координат середины отрезка в случае его расположения на осях абсцисс и ординат, а также при перпендикулярности одной из них. Следовательно, координаты центра отрезка AB, находящегося в плоскости и ограниченного точками A(xA,yA) и B(xB,yB), вычисляются следующим образом:
(left(frac{x_A+x_B}2,frac{y_A+y_B}2right))
Середина отрезка в пространстве
Допустим, что в трехмерной системе координат Oxyz любые две точки с соответствующими им координатами A(xA, yA, zA) и B(xB, yB, zB). C(xC, yC, zC) — это центр АВ. Задание заключается в том, чтобы определить xC, yC, zC.
Проведем от исходных точек перпендикуляры к прямым Ox, Oy и Oz. Образовавшиеся точки пересечения с координатными осями — Ax, Ay, Az; Bx, By, Bz; Cx, Cy, Cz — проекции точек A, B, C на них.
Воспользуемся теоремой Фалеса:
(left|A_xC_xright|=left|C_xB_xright|)
(left|A_yC_yright|=left|C_yB_yright|)
(left|A_zC_zright|=left|C_zB_zright|)
Исходя из полученных равенств следует, что Cx, Cy, Cz — делят AxBx, AyBy, AzBz пополам, то есть являются серединами перечисленных отрезков. Значит, для определения координат центра AB с концами A(xA,yA,zA) и B(xB,yB,zB) используем формулу:
(left(frac{x_A+x_B}2,frac{y_A+y_B}2,;frac{z_A+z_B}2right))
Метод с использованием координат радиус-векторов концов отрезка
Трактовка векторов в алгебре позволяет составить формулу для расчета координат середины отрезка.
Дано: прямоугольная система координат Oxy, в которой лежат произвольные точки A(xA,yA) и B(xB,yB), а также C, делящая пополам отрезок, ограниченный A и B.
По определению действий над вектором в геометрии:
((1);overrightarrow{OC}=frac12timesleft(overrightarrow{OA}+overrightarrow{OB}right))
В рассматриваемой ситуации в точке C пересекаются диагонали параллелограмма с основаниями: (overrightarrow{OA},;overrightarrow{OB}
).
Это значит, что С — это центр диагоналей.
Поскольку координаты радиус вектора совпадают с координатами точки, имеем: (overrightarrow{OA}=left(x_A,;y_Aright),;overrightarrow{OB}=left(x_B,;y_Bright)
).
Произведем подстановку в формулу (1):
(overrightarrow{OC}=frac12timesleft(overrightarrow{OA}+overrightarrow{OB}right)=left(frac{x_A+x_B}2,;frac{y_A+y_B}2right)
).
Получили формулу определения координат середины отрезка, находящегося в декартовой системе координат:
(left(frac{x_A+x_B}2,;frac{y_A+y_B}2right))
По аналогично схеме можно вывести формулу для расчета координат центра отрезка, лежащего в пространстве:
(left(frac{x_A+x_B}2,frac{y_A+y_B}2,;frac{z_A+z_B}2right))
Примеры решения задач
Задача № 1
Дано: в декартовой системе координат имеются точки M(5,4) и N(1,−2). Найти координаты середины отрезка MN.
Решение:
Пусть точка O — центр MN. Тогда вычислим ее координаты, подставив в формулы:
(x_O=frac{x_A+x_B}2=frac{5+1}2=frac62=3)
(y_O=frac{y_A+y_B}2=frac{4+left(-2right)}2=frac{4-2}2=frac22=1)
Точка O имеет координаты (3,1).
Ответ: (3,1).
Задача № 2
Дано: треугольник ABC лежит в прямоугольной системе координат. Известны координаты его вершин: A(7,3), B(−3,1), C(2,4). Вычислите длину медианы АМ.
Решение:
Поскольку АМ является медианой треугольника ABC, то точка М делит сторону ВС на два равных отрезка, то есть является серединой отрезка ВС. Отсюда можно вычислить координат точки М:
(x_М=frac{x_В+x_С}2=frac{-3+2}2=frac{-1}2=-0,5)
(y_М=frac{y_В+y_С}2=frac{1+4}2=frac52=2,5)
Теперь, зная координаты начала и конца отрезка АМ, применим формулу нахождения расстояния между точками:
(AM=sqrt{left(x_M-x_Aright)^2+left(y_M-y_Aright)^2}=sqrt{left(-0,5-7right)^2+left(-2,5-3right)^2}=sqrt{-7,5^2+left(-5,5right)^2}=sqrt{56,25+30,25}=sqrt{86,5}
).
Ответ: √86,5.


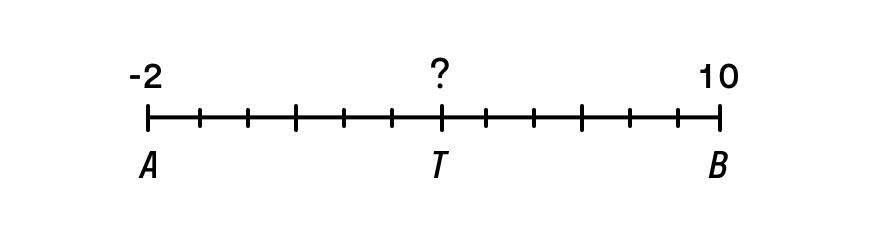
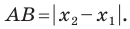
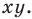
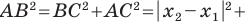
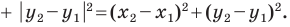

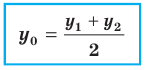
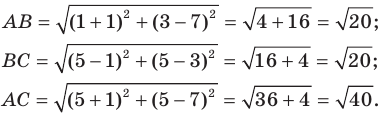

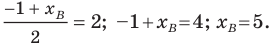
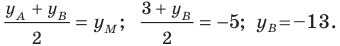
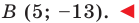
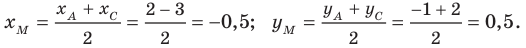
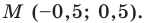
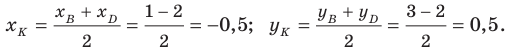
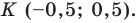
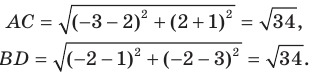

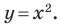
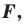 то ее координаты являются решением данного уравнения;
то ее координаты являются решением данного уравнения;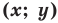 данного уравнения является координатами точки, принадлежащей фигуре
данного уравнения является координатами точки, принадлежащей фигуре