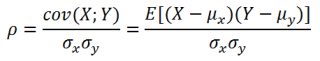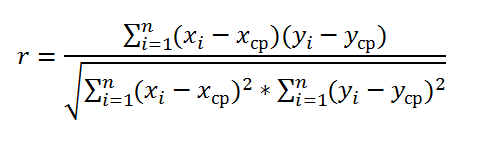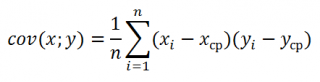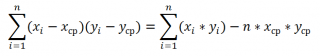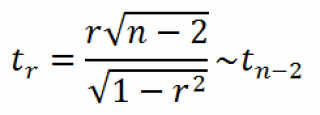Определить, какие акции купить для вашего портфеля, чтобы быть финансово безопасным, но при этом получать деньги, может быть огромным усилием. Ковариация — это один из показателей, который вы можете использовать для анализа риска добавления еще одной акции в свой портфель.
Знание того, как рассчитать ковариацию, может дать вам представление о взаимосвязи между двумя акциями, независимо от того, есть ли они у вас или те, которые вы рассматриваете в будущем. В этой статье мы обсудим, что такое ковариация, чем она отличается от дисперсии, как ее рассчитать за шесть шагов, ее применение и пример расчета.
Что такое ковариация?
Ковариация — это измерение, используемое в статистике для определения того, изменяются ли две переменные в одном и том же направлении. Это измерение разницы между двумя переменными, и две переменные, используемые для определения ковариации, не связаны между собой.
Вы можете измерить ковариацию с точки зрения единиц, связанных с двумя переменными в наборах данных. Например, в финансах два набора данных могут быть стоимостью акций одной компании, а другой — акциями несвязанной компании. Поскольку обе величины представлены в долларах, единицей измерения будут доллары.
Ковариация сравнивает две переменные с точки зрения положительного и отрицательного. Если значение ковариации отрицательное, то две переменные движутся в противоположных направлениях. Если значение ковариации положительное, то две переменные движутся в одном направлении.
Примечательно, что это означает, что две переменные могут уменьшаться в одном и том же направлении, и ковариация все равно будет иметь положительное значение. Например, если две компании владеют акциями, которые со временем дешевеют, то их ковариация будет положительной.
Ковариация против дисперсии
Дисперсия — это измерение расстояния между переменной и средним значением набора данных. В отличие от ковариации, одна точка данных или тенденция является средним значением, а другая представляет собой интересующую точку или тенденцию, которую вы решили измерить.
Используя приведенный выше пример, если акции первой компании растут с течением времени, но общая тенденция для всех акций падает, то разница между средним значением и акциями компании может увеличиться. Если акции второй компании также растут с той же скоростью, что и акции первой, то ковариация будет положительной.
Как рассчитать ковариацию
Для расчета ковариации можно использовать формулу:
Cov(X, Y) = Σ(Xi-µ)(Yj-v)/n
Где части уравнения:
-
Cov(X, Y) представляет собой ковариацию переменных X и Y.
-
Σ представляет собой сумму других частей формулы.
-
(Xi) представляет все значения переменной X.
-
µ представляет собой среднее значение переменной X.
-
Yj представляет все значения переменной Y.
-
v представляет собой среднее значение Y-переменной.
-
Σ представляет собой сумму значений для (Xi-µ) и (Yj-v).
-
n представляет собой общее количество точек данных по обеим переменным.
Вы можете использовать следующие шаги и формулу ковариации, чтобы найти ковариацию ваших данных:
1. Получите данные
Первым шагом в нахождении ковариации двух переменных является сбор данных для обоих наборов. Например, в таблице ниже показана стоимость акций двух новых компаний в период с 2015 по 2020 год:
Год Компания X Стоимость акций ($) Компания Y Стоимость акций ($) 2015 1 245 100 2016 1 415 123 2017 1 312 129 2018 1 427 143 2019 1 510 150 2020 1 590 197
2. Рассчитайте среднее значение для каждой переменной
Чтобы найти среднее значение для каждой акции, сложите все значения X вместе и разделите на общее количество значений X. Затем сделайте то же самое для значений Y:
-
µ = 1 245 + 1 415 + 1 312 + 1 427 + 1 510 + 1 590 / 6
-
µ = 1416,5
-
v = 100 + 123 + 129 + 143 + 150 + 197 / 6
-
v = 140,3
3. Найдите разницу между каждым значением и средним значением для обеих переменных.
Вычтите среднее значение для каждого набора переменных из каждой переменной в этом наборе. Например:
Год Компания X (Xi-µ) Компания Y (Yj-v) 2015 1 245 — 1 416,5 = -171,5 100 — 140,3 = -40,3 2016 1 415 — 1 416,5 = -1,5 123 — 140,3 = -17,3 2017 1 312 — 1 416,5 = -1 209,5 140,2 = -11,2 2018 г. 1 427 — 1 416,5 = 10,5 143 — 140,3 = 2,7 2019 г. 1 510 — 1 416,5 = 93,5 150 — 140,3 = 9,7 2020 г. 1 590 — 1 416,5 = 5 6,7 — 4 0,7
4. Умножьте значения двух переменных
Как только вы нашли значения для обеих переменных на предыдущем шаге, вы можете перемножить их вместе. Например:
Год Компания X (Xi-µ) Компания Y (Yj-v) (Xi-µ)(Yj-v) 2015 1 245 — 1 416,5 = -171,5 100 — 140,3 = -40,3 (-171,5)(-40,3) = 6 911,45 2016 1 415 — 1 416,5 = -1,5 123 — 140,3 = -17,3 (-1,5)(-17,3) = 25,95 2017 1 312 — 1 416,5 = -104,5 129 — 140,2 = -11,2 (-104,5)(-11,3) = 1 180,85 2016 — 1 4218 1 143 — 140,3 = 2,7 (10.5) (2.7) = 28,35 2019 1,510 — 140,3 — 93,5 150 — 140,3 = 9,7 (93,5) (9.7) = 906,95 2020 1 590 — 1 416,5 = 173,5 197 — 140,3 = 56,7 (173,5) (56.7) = 9 837,45
5. Сложите значения вместе
После того, как вы вычислили произведение двух переменных вместе, вы можете сложить значения, чтобы получить предпоследнюю часть уравнения. Например, вы можете добавить значения продуктов из компаний выше, чтобы получить сумму всех значений:
6 911,45 + 25,95 + 1 180,85 + 28,35 + 906,95 + 9 837,45 = 18 891
6. Используйте значения из предыдущих шагов, чтобы найти ковариацию данных.
После того, как вы рассчитали части уравнения, вы можете ввести в него свои значения. Например, вы можете поместить акции компании сверху в уравнение, как показано ниже:
Cov(X, Y) = 18 891/6
Где значения:
-
18 891 = Σ(Xi-µ)(Yj-v)
-
6 = п
Как подсчитано выше, ковариация акций компании X и компании Y составляет 3148,5. Положительный характер значения ковариации показывает, что акции двух компаний движутся в одном направлении.
Приложения ковариации
Одно применение ковариации в финансах. Вы можете использовать ковариацию для оценки риска конкретных акций, сравнивая, движутся ли они вместе или против друг друга. Например, если стоимость двух акций увеличивается и уменьшается противоположно друг другу, то они будут дополнять друг друга с минимальным риском, потому что они минимизируют финансовые потери, поскольку одна растет, а другая сокращается.
Вы также можете использовать ковариацию с корреляцией, чтобы определить, движутся ли переменные вместе и как, и инвесторы часто используют и то, и другое, чтобы определить, добавлять ли акции в портфель. В то время как ковариация может сказать вам, как двигаются два или более набора данных, корреляция может сказать вам, какие другие факторы влияют на это движение и связаны ли две переменные друг с другом.
Пример расчета
Ниже приведен пример расчета ковариации продаж двух новых игрушек, проданных одной и той же компанией:
1. Найдите свои данные
Сначала найдите интересующие вас данные. В данном примере это количество двух игрушек, проданных с января по апрель:
Месяц Игрушка X Игрушка Y 12 января 67 13 февраля 45 25 марта 32 39 апреля 21
2. Найдите количество проданных игрушек
Затем найдите количество игрушек, проданных за указанные выше месяцы, и вы сможете найти среднее количество игрушек, проданных для каждой из них:
-
µ = 12 + 13 + 25 + 39 / 4
-
м = 22,25
-
v = 67 + 45 + 32 + 21/4
-
v = 41,25
3. Найдите разницу в значениях
В-третьих, вычислите разницу между каждым значением X и µ. Затем вычислите разницу между каждым значением Y и v:
Месяц Toy X (Xi-µ) Toy Y (Yj-v) 12 января — 22,25 = -10,25 67 — 41,25 = 25,75 13 февраля — 22,25 = -9,25 45 — 41,25 = 3,75 25 марта — 22,25 = 2,75 32 — 41,25 = — 9,25 39 апреля — 22,25 = 16,75 21 — 41,25 = -20,25
4. Рассчитайте произведение
В-четвертых, вы можете вычислить произведение (Xi-µ) и (Yj-v):
-
(-10,25)(25,75) = -263,94
-
(-9,25)(3,75) = -34,69
-
(2,75)(-9,25) = -25,44
-
(16,75)(-20,25) = -339,19
5. Добавляйте товары вместе
В-пятых, вы можете сложить произведения драгоценных вычислений, чтобы получить сумму -663,26:
-
Σ = (-263,94) + (-34,69) + (-25,44) + (-339,19) = -663,26
6. Замените значения
Наконец, вы можете подставить значения в уравнение из предыдущего:
-
Cov(X, Y) = -663,26/4
-
Cov(X, Y) = -165,82
Используя эту ковариацию, вы можете определить, что когда количество проданных игрушек увеличивается для одной игрушки, оно уменьшается для другой. Это связано с тем, что значение ковариации отрицательно.
Ковариация
Характеристикой
зависимости между случайными величинами
X
и Y
служит математическое ожидание
произведения отклонений X
и Y от их
центров распределений (так иногда
называют математическое ожидание
случайной величины), которое называется
коэффициентом ковариации или просто
ковариацией.
Cov(X;Y) = E((X–EX)(Y–EY))
Пусть
X = x1,
x2,
x3,,
xn,
Y= y1,
y2,
y3,,yn.
Тогда
Cov(X;Y)=
Эту
формулу можно интерпретировать так.
Если при больших значениях Х
более вероятны большие значения Y,
а при малых значениях X
более вероятны малые значения Y,
то в правой части формулы ковариации
положительные слагаемые
доминируют, и ковариация принимает
положительные значения.
Если
же более вероятны произведения
(xi – EX)(yj – EY),
состоящие из сомножителей разного
знака, то есть исходы случайного
эксперимента, приводящие к большим
значениям X
в основном приводят к малым значениям
Y и наоборот,
то ковариация принимает большие по
модулю отрицательные значения.
В
первом случае принято говорить о прямой
связи: с ростом X
случайная величина Y
имеет тенденцию к возрастанию.
Во
втором случае говорят об обратной связи:
с ростом X
случайная величина Y
имеет тенденцию к уменьшению или падению.
Если
примерно одинаковый вклад в сумму дают
и положительные и отрицательные
произведения (xi – EX)(yj – EY)pij,
то можно сказать, что в сумме они будут
“гасить” друг друга и ковариация будет
близка к нулю. В этом случае не
просматривается зависимость одной
случайной величины от другой.
Легко
показать, что если
P((X = xi)∩(Y = yj)) = P(X = xi)P(Y = yj)
(i = 1,2,,n;
j = 1,2,,k),
то
cov(X;Y)=
0.
Действительно
из (2) следует
Здесь
использовано очень важное свойство
математического ожидания: математическое
ожидание отклонения случайной величины
от ее математического ожидания равно
нулю.
Ковариацию
удобно представлять в виде
Cov(X;Y)=E(XY–XEY–YEX+EXEY)=E(XY)–E(XEY)–E(YEX)+E(EXEY)=
=E(XY)–EXEY–EXEY+EXEY=E(XY)–EXEY
Ковариация
двух случайных величин равна математическому
ожиданию их произведения минус
произведение математических ожиданий.
Поскольку
для независимых случайных величин EXY
= EXEY,
то, очевидно, что для
независимых случайных величин X
и Y cov(X;Y)=0.
Определение.
Случайные величины, ковариация которых
равна нулю, называют некоррелированными.
!!!
Замечание.
Как было
показано выше, из независимости случайных
величин следует их некоррелированность,
то есть равенство нулю корреляции.
Обратное
неверно! Рассмотрим
соответствующий пример:
Пусть
случайная величина Х имеет равномерное
распределение на интервале (-1, 1), а
случайная величина Y
связана со случайной величиной Х
функциональной зависимостью Y=X2
. Покажем, что cov
(X,Y)=0,
хотя налицо функциональная зависимость
.
Учитывая
, что ЕХ=0 (середина интервала (-1,1)),
получаем:
cov
(X,Y)=EXY-EXEY=EX3
=
Итак,
из некоррелированности случайных
величин не следует их независимость.
Ковариация
случайных величин отражает степень
близости зависимости случайных величин
к линейной, то есть, к зависимости вида
Y=aX+b.
Рассмотрим
теперь еще одну меру линейной зависимости
– коэффициент
корреляции
случайных величин Х и Y
r(X,Y)
=
Может
возникнуть вопрос, зачем вводить еще
одну меру линейной зависимости?
-
Коэффициент
корреляции меняется от -1 до 1, а не по
всей числовой оси -
Коэффициент
корреляции, в отличие от ковариации,
нечувствителен к смене единиц измерения -
Если
случайные величины независимы, то
коэффициент корреляции, как и ковариация,
равен нулю. -
Если
случайные величины линейно зависимы,
то r=1
– прямая зависимость , r=-1,
обратная. И наоборот, из равенства по
модулю 1 следует линейная зависимость.
Пусть
распределение случайных величин задано
таблицей
ЕХ1
ЕХ2
DX1
= EX1
2
– (EX1)2=
0,59
DX2
= EX2
2
– (EX2)2=
0,2475
Cov
(X1
,X2
)= E (X1
,X2
)–E X1
EX2
E
(X1
,X2
) =
Замечание.
Ковариационная и корреляционная матрицы
– это таблицы, состоящие соответственно
из ковариаций и коэффициентов корреляций
соответствующих случайных величин.
(Заметим, что по главной диагонали
корреляционной матрицы стоят 1 –
случайная величина, очевидно, находится
сама с собой в линейной зависимости).
Используются эти матрицы для наглядного
представления данных о связи величин
и в статистике.
Соседние файлы в папке Модуль 1. Лекции
- #
- #
- #
- #
- #
- #
- #
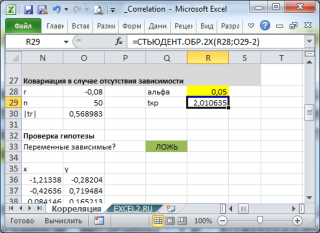
Вычислим коэффициент корреляции и ковариацию для разных типов взаимосвязей случайных величин.
Коэффициент корреляции
(
критерий корреляции
Пирсона, англ. Pearson Product Moment correlation coefficient)
определяет степень
линейной
взаимосвязи между случайными величинами.
где Е[…] – оператор
математического ожидания
, μ и σ –
среднее
случайной величины и ее
стандартное отклонение
.
Как следует из определения, для вычисления
коэффициента корреляции
требуется знать распределение случайных величин Х и Y. Если распределения неизвестны, то для оценки
коэффициента корреляции
используется
выборочный коэффициент корреляции
r
(
еще он обозначается как
R
xy
или
r
xy
)
:
Как видно из формулы для расчета
корреляции
, знаменатель (произведение стандартных отклонений с точностью до безразмерного множителя) просто нормирует числитель таким образом, что
корреляция
оказывается безразмерным числом от -1 до 1.
Корреляция
и
ковариация
предоставляют одну и туже информацию, но
корреляцией
удобнее пользоваться, т.к. она является безразмерной величиной.
Рассчитать
коэффициент корреляции
и
ковариацию выборки
в MS EXCEL не представляет труда, так как для этого имеются специальные функции
КОРРЕЛ()
и
КОВАР()
. Гораздо сложнее разобраться, как интерпретировать полученные значения, большая часть статьи посвящена именно этому.
Теоретическое отступление
Напомним, что
корреляционной связью
называют статистическую связь, состоящую в том, что различным значениям одной переменной соответствуют различные
средние
значения другой (с изменением значения Х
среднее значение
Y изменяется закономерным образом). Предполагается, что
обе
переменные Х и Y являются
случайными
величинами и имеют некий случайный разброс относительно их
среднего значения
.
Примечание
. Если случайную природу имеет только одна переменная, например, Y, а значения другой являются детерминированными (задаваемыми исследователем), то можно говорить только о регрессии.
Таким образом, например, при исследовании зависимости среднегодовой температуры нельзя говорить о
корреляции
температуры и года наблюдения и, соответственно, применять показатели
корреляции
с соответствующей их интерпретацией.
Корреляционная связь
между переменными может возникнуть несколькими путями:
-
Наличие причинной зависимости между переменными. Например, количество инвестиций в научные исследования (переменная Х) и количество полученных патентов (Y). Первая переменная выступает как
независимая переменная (фактор)
, вторая —
зависимая переменная (результат)
. Необходимо помнить, что зависимость величин обуславливает наличие корреляционной связи между ними, но не наоборот. - Наличие сопряженности (общей причины). Например, с ростом организации растет фонд оплаты труда (ФОТ) и затраты на аренду помещений. Очевидно, что неправильно предполагать, что аренда помещений зависит от ФОТ. Обе этих переменных во многих случаях линейно зависят от количества персонала.
- Взаимовлияние переменных (при изменении одной, вторая переменная изменяется, и наоборот). При таком подходе допустимы две постановки задачи; любая переменная может выступать как в роли независимой переменной и в роли зависимой.
Таким образом,
показатель корреляции
показывает, насколько сильна
линейная взаимосвязь
между двумя факторами (если она есть), а регрессия позволяет прогнозировать один фактор на основе другого.
Корреляция
, как и любой другой статистический показатель, при правильном применении может быть полезной, но она также имеет и ограничения по использованию. Если
диаграмма рассеяния
показывает четко выраженную линейную зависимость или полное отсутствие взаимосвязи, то
корреляция
замечательно это отразит. Но, если данные показывают нелинейную взаимосвязь (например, квадратичную), наличие отдельных групп значений или выбросов, то вычисленное значение
коэффициента корреляции
может ввести в заблуждение (см.
файл примера
).
Корреляция
близкая к 1 или -1 (т.е. близкая по модулю к 1) показывает сильную линейную взаимосвязь переменных, значение близкое к 0 показывает отсутствие взаимосвязи. Положительная
корреляция
означает, что с ростом одного показателя другой в среднем увеличивается, а при отрицательной – уменьшается.
Для вычисления коэффициента корреляции требуется, чтобы сопоставляемые переменные удовлетворяли следующим условиям:
- количество переменных должно быть равно двум;
-
переменные должны быть количественными (например, частота, вес, цена). Вычисленное среднее значение этих переменных имеет понятный смысл: средняя цена или средний вес пациента. В отличие от количественных, качественные (номинальные) переменные принимают значения лишь из конечного набора категорий (например, пол или группа крови). Этим значениям условно сопоставлены числовые значения (например, женский пол – 1, а мужской – 2). Понятно, что в этом случае вычисление
среднего значения
, которое требуется для нахождения
корреляции
, некорректно, а значит некорректно и вычисление самой
корреляции
; -
переменные должны быть случайными величинами и иметь
нормальное распределение
.
Двумерные данные могут иметь различную структуру. Для работы с некоторыми из них требуются определенные подходы:
-
Для данных с нелинейной связью
корреляцию
нужно использовать с осторожностью. Для некоторых задач бывает полезно преобразовать одну или обе переменных так, чтобы получить линейную взаимосвязь (для этого требуется сделать предположение о виде нелинейной связи, чтобы предложить нужный тип преобразования). -
С помощью
диаграммы рассеяния
у некоторых данных можно наблюдать неравную вариацию (разброс). Проблема неодинаковой вариации состоит в том, что места с высокой вариацией не только предоставляют наименее точную информацию, но и оказывают наибольшее влияние при расчете статистических показателей. Эту проблему также часто решают с помощью преобразования данных, например, с помощью логарифмирования. - У некоторых данных можно наблюдать разделение на группы (clustering), что может свидетельствовать о необходимости разделения совокупности на части.
- Выброс (резко отклоняющееся значение) может исказить вычисленное значение коэффициента корреляции. Выброс может быть причиной случайности, ошибки при сборе данных или могут действительно отражать некую особенность взаимосвязи. Так как выброс сильно отклоняется от среднего значения, то он вносит большой вклад при расчете показателя. Часто расчет статистических показателей производят с и без учета выбросов.
Использование MS EXCEL для расчета корреляции
В качестве примера возьмем 2 переменные
Х
и
Y
и, соответственно,
выборку
состоящую из нескольких пар значений (Х
i
; Y
i
). Для наглядности построим
диаграмму рассеяния
.
Примечание
: Подробнее о построении диаграмм см. статью
Основы построения диаграмм
. В
файле примера
для построения
диаграммы рассеяния
использована
диаграмма График
, т.к. мы здесь отступили от требования случайности переменной Х (это упрощает генерацию различных типов взаимосвязей: построение трендов и заданный разброс). В случае реальных данных необходимо использовать диаграмму типа Точечная (см. ниже).
Расчеты
корреляции
проведем для различных случаев взаимосвязи между переменными:
линейной, квадратичной
и при
отсутствии связи
.
Примечание
: В
файле примера
можно задать параметры линейного тренда (наклон, пересечение с осью Y) и степень разброса относительно этой линии тренда. Также можно настроить параметры квадратичной зависимости.
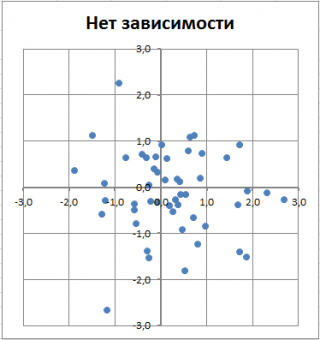
В
файле примера
для построения
диаграммы рассеяния
в случае отсутствия зависимости переменных использована диаграмма типа Точечная. В этом случае точки на диаграмме располагаются в виде облака.
Примечание
: Обратите внимание, что изменяя масштаб диаграммы по вертикальной или горизонтальной оси, облаку точек можно придать вид вертикальной или горизонтальной линии. Понятно, что при этом переменные останутся независимыми.
Как было сказано выше, для расчета
коэффициента корреляции
в MS EXCEL существует функций
КОРРЕЛ()
. Также можно воспользоваться аналогичной функцией
PEARSON()
, которая возвращает тот же результат.
Для того, чтобы удостовериться, что вычисления
корреляции
производятся функцией
КОРРЕЛ()
по вышеуказанным формулам, в
файле примера
приведено вычисление
корреляции
с помощью более подробных формул:
=
КОВАРИАЦИЯ.Г(B28:B88;D28:D88)/СТАНДОТКЛОН.Г(B28:B88)/СТАНДОТКЛОН.Г(D28:D88)
=
КОВАРИАЦИЯ.В(B28:B88;D28:D88)/СТАНДОТКЛОН.В(B28:B88)/СТАНДОТКЛОН.В(D28:D88)
Примечание
: Квадрат
коэффициента корреляции
r равен
коэффициенту детерминации
R2, который вычисляется при построении линии регрессии с помощью функции
КВПИРСОН()
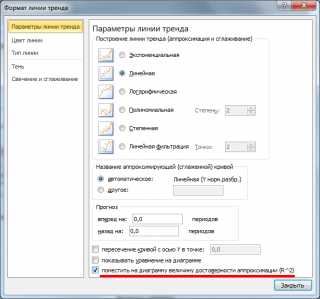
. Значение R2 также можно вывести на
диаграмме рассеяния
, построив линейный тренд с помощью стандартного функционала MS EXCEL (выделите диаграмму, выберите вкладку
Макет
, затем в группе
Анализ
нажмите кнопку
Линия тренда
и выберите
Линейное приближение
). Подробнее о построении линии тренда см., например, в
статье о методе наименьших квадратов
.
Использование MS EXCEL для расчета ковариации
Ковариация
близка по смыслу с
дисперсией
(также является мерой разброса) с тем отличием, что она определена для 2-х переменных, а
дисперсия
— для одной. Поэтому, cov(x;x)=VAR(x).
Для вычисления ковариации в MS EXCEL (начиная с версии 2010 года) используются функции
КОВАРИАЦИЯ.Г()
и
КОВАРИАЦИЯ.В()
. В первом случае формула для вычисления аналогична вышеуказанной (окончание
.Г
обозначает
Генеральная совокупность
), во втором – вместо множителя 1/n используется 1/(n-1), т.е. окончание
.В
обозначает
Выборка
.
Примечание
: Функция
КОВАР()
, которая присутствует в MS EXCEL более ранних версий, аналогична функции
КОВАРИАЦИЯ.Г()
.
Примечание
: Функции
КОРРЕЛ()
и
КОВАР()
в английской версии представлены как CORREL и COVAR. Функции
КОВАРИАЦИЯ.Г()
и
КОВАРИАЦИЯ.В()
как COVARIANCE.P и COVARIANCE.S.
Дополнительные формулы для расчета
ковариации
:
=
СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88-СРЗНАЧ(D28:D88)))/СЧЁТ(D28:D88)
=
СУММПРОИЗВ(B28:B88-СРЗНАЧ(B28:B88);(D28:D88))/СЧЁТ(D28:D88)
=
СУММПРОИЗВ(B28:B88;D28:D88)/СЧЁТ(D28:D88)-СРЗНАЧ(B28:B88)*СРЗНАЧ(D28:D88)
Эти формулы используют свойство
ковариации
:
Если переменные
x
и
y
независимые, то их ковариация равна 0. Если переменные не являются независимыми, то дисперсия их суммы равна:
VAR(x+y)= VAR(x)+ VAR(y)+2COV(x;y)
А
дисперсия
их разности равна
VAR(x-y)= VAR(x)+ VAR(y)-2COV(x;y)
Оценка статистической значимости коэффициента корреляции
При проверке значимости
коэффициента корреляции
нулевая гипотеза состоит в том, что
коэффициент корреляции
равен нулю, альтернативная — не равен нулю (про
проверку гипотез
см. статью
Проверка гипотез
).
Для того чтобы проверить гипотезу, мы должны знать распределение случайной величины, т.е.
коэффициента корреляции
r. Обычно, проверку гипотезы осуществляют не для r, а для случайной величины t
r
:
которая имеет
распределение Стьюдента
с n-2 степенями свободы.
Если вычисленное значение случайной величины |t
r
| больше, чем критическое значение t
α,n-2
(α- заданный
уровень значимости
), то нулевую гипотезу отклоняют (взаимосвязь величин является статистически значимой).
Надстройка Пакет анализа
В
надстройке Пакет анализа
для вычисления ковариации и корреляции
имеются одноименные инструменты
анализа
.
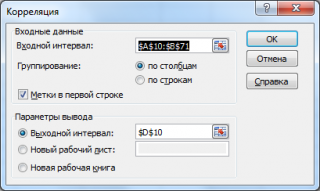
После вызова инструмента появляется диалоговое окно, которое содержит следующие поля:
Входной интервал
: нужно ввести ссылку на диапазон с исходными данными для 2-х переменных
Группирование
: как правило, исходные данные вводятся в 2 столбца
Метки в первой строке
: если установлена галочка, то
Входной интервал
должен содержать заголовки столбцов. Рекомендуется устанавливать галочку, чтобы результат работы Надстройки содержал информативные столбцы
Выходной интервал
: диапазон ячеек, куда будут помещены результаты вычислений. Достаточно указать левую верхнюю ячейку этого диапазона.
Надстройка возвращает вычисленные значения корреляции и ковариации (для ковариации также вычисляются дисперсии обоих случайных величин).
Двумерной называют случайную величину
, возможные значения
которой есть пары чисел
. Составляющие
и
, рассматриваемые
одновременно, образуют систему двух случайных величин. Двумерную величину
геометрически можно истолковать как случайную точку
на плоскости
либо как случайный вектор
.
Дискретной называют двумерную величину, составляющие которой дискретны.
Закон распределения дискретной двумерной СВ.
Безусловные и условные законы распределения составляющих
Законом распределения вероятностей двумерной случайной величины называют соответствие
между возможными значениями и их вероятностями.
Закон
распределения дискретной двумерной случайной величины может быть задан:
а) в
виде таблицы с двойными входом, содержащей возможные значения и их вероятности;
б) аналитически, например в виде функции распределения.
Зная
закон распределения двумерной дискретной случайной величины, можно найти законы
каждой из составляющих. В общем случае, для того чтобы найти вероятность
, надо просуммировать
вероятности столбца
. Аналогично сложив
вероятности строки
получим вероятность
.
Пусть
составляющие
и
дискретны и имеют соответственно следующие
возможные значения:
;
.
Условным распределением составляющей
при
(j сохраняет одно и то же
значение при всех возможных значениях
) называют совокупность
условных вероятностей:
Аналогично
определяется условное распределение
.
Условные
вероятности составляющих
и
вычисляют соответственно по формулам:
Для
контроля вычислений целесообразно убедиться, что сумма вероятностей условного
распределения равна единице.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Ковариация (корреляционный момент)
Ковариация двух случайных величин характеризует степень зависимости случайных величин, так
и их рассеяние вокруг точки
.
Ковариацию
(корреляционный момент) можно найти по формуле:
Свойства ковариации
Свойство 1.
Ковариация двух независимых случайных величин равна нулю.
Свойство 2.
Ковариация двух случайных величин равна математическому ожиданию их
произведение математических ожиданий.
Свойство 3.
Ковариация двухмерной случайной величины по абсолютной случайной величине не
превосходит среднеквадратических отклонений своих компонентов.
Коэффициент корреляции
Коэффициент корреляции – отношение ковариации двухмерной случайной
величины к произведению среднеквадратических отклонений.
Формула коэффициента корреляции:
Две
случайные величины
и
называют коррелированными, если их коэффициент
корреляции отличен от нуля.
и
называют некоррелированными величинами, если
их коэффициент корреляции равен нулю
Свойства коэффициента корреляции
Свойство 1.
Коэффициент корреляции двух независимых случайных величин равен нулю. Отметим,
что обратное утверждение неверно.
Свойство 2.
Коэффициент корреляции двух случайных величин не превосходит по абсолютной
величине единицы.
Свойство 3.
Коэффициент корреляции двух случайных величин равен по модулю единице тогда и
только тогда, когда между величинами существует линейная функциональная
зависимость.
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Линейная регрессия
Рассмотрим
двумерную случайную величину
, где
и
– зависимые случайные величины. Представим
одну из величины как функцию другой. Ограничимся приближенным представлением
величины
в виде линейной функции величины
:
где
и
– параметры, подлежащие определению. Это можно
сделать различными способами и наиболее употребительный из них – метод
наименьших квадратов.
Линейная
средняя квадратическая регрессия
на
имеет вид:
Коэффициент
называют
коэффициентом регрессии
на
, а прямую
называют
прямой среднеквадратической регрессии
на
.
Аналогично
можно получить прямую среднеквадратической регрессии
на
:
Смежные темы решебника:
- Двумерная непрерывная случайная величина
- Линейный выборочный коэффициент корреляции
- Парная линейная регрессия и метод наименьших квадратов
Задача 1
Закон
распределения дискретной двумерной случайной величины (X,Y) задан таблицей.
Требуется:
—
определить одномерные законы распределения случайных величин X и Y;
— найти
условные плотности распределения вероятностей величин;
—
вычислить математические ожидания mx и my;
—
вычислить дисперсии σx и σy;
—
вычислить ковариацию μxy;
—
вычислить коэффициент корреляции rxy.
| xy | 3 | 5 | 8 | 10 | 12 |
| -1 | 0.04 | 0.04 | 0.03 | 0.03 | 0.01 |
| 1 | 0.04 | 0.07 | 0.06 | 0.05 | 0.03 |
| 3 | 0.05 | 0.08 | 0.09 | 0.08 | 0.05 |
| 6 | 0.03 | 0.04 | 0.04 | 0.06 | 0.08 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 2
Задана
дискретная двумерная случайная величина (X,Y).
а) найти
безусловные законы распределения составляющих; б) построить регрессию случайной
величины Y на X; в) построить регрессию случайной величины X на Y; г) найти коэффициент ковариации; д) найти
коэффициент корреляции.
| Y | X | ||||
| 1 | 2 | 3 | 4 | 5 | |
| 30 | 0.05 | 0.03 | 0.02 | 0.01 | 0.01 |
| 40 | 0.03 | 0.02 | 0.02 | 0.04 | 0.01 |
| 50 | 0.05 | 0.03 | 0.02 | 0.02 | 0.01 |
| 70 | 0.1 | 0.03 | 0.04 | 0.03 | 0.01 |
| 90 | 0.1 | 0.04 | 0.01 | 0.07 | 0.2 |
Задача 3
Двумерная случайная величина (X,Y) задана
таблицей распределения. Найти законы распределения X и Y, условные
законы, регрессию и линейную регрессию Y на X.
|
x y |
1 | 2 | 3 |
| 1.5 | 0.03 | 0.02 | 0.02 |
| 2.9 | 0.06 | 0.13 | 0.03 |
| 4.1 | 0.4 | 0.07 | 0.02 |
| 5.6 | 0.15 | 0.06 | 0.01 |
Задача 4
Двумерная
случайная величина (X,Y) распределена по закону
| XY | 1 | 2 |
| -3 | 0,1 | 0,2 |
| 0 | 0,2 | 0,3 |
| -3 | 0 | 0,2 |
Найти
законы распределения случайных величины X и Y, условный закон
распределения Y при X=0 и вычислить ковариацию.
Исследовать зависимость случайной величины X и Y.
Задача 5
Случайные
величины ξ и η имеют следующий совместный закон распределения:
P(ξ=1,η=1)=0.14
P(ξ=1,η=2)=0.18
P(ξ=1,η=3)=0.16
P(ξ=2,η=1)=0.11
P(ξ=2,η=2)=0.2
P(ξ=2,η=3)=0.21
1)
Выписать одномерные законы распределения случайных величин ξ и η, вычислить
математические ожидания Mξ, Mη и дисперсии Dξ, Dη.
2) Найти
ковариацию cov(ξ,η) и коэффициент корреляции ρ(ξ,η).
3)
Выяснить, зависимы или нет события {η=1} и {ξ≥η}
4)
Составить условный закон распределения случайной величины γ=(ξ|η≥2) и найти Mγ и
Dγ.
Задача 6
Дан закон
распределения двумерной случайной величины (ξ,η):
| ξ=-1 | ξ=0 | ξ=2 | |
| η=1 | 0,1 | 0,1 | 0,1 |
| η=2 | 0,1 | 0,2 | 0,1 |
| η=3 | 0,1 | 0,1 | 0,1 |
1) Выписать одномерные законы
распределения случайных величин ξ и η, вычислить математические ожидания Mξ,
Mη и дисперсии Dξ, Dη
2) Найти ковариацию cov(ξ,η) и
коэффициент корреляции ρ(ξ,η).
3) Являются ли случайные события |ξ>0|
и |η> ξ | зависимыми?
4) Составить условный закон
распределения случайной величины γ=(ξ|η>0) и найти Mγ и Dγ.
Задача 7
Дано
распределение случайного вектора (X,Y). Найти ковариацию X и Y.
| XY | 1 | 2 | 4 |
| -2 | 0,25 | 0 | 0,25 |
| 1 | 0 | 0,25 | 0 |
| 3 | 0 | 0,25 | 0 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 8
Случайные
приращения цен акций двух компаний за день имеют совместное распределение,
заданное таблицей. Найти ковариацию этих случайных величин.
| YX | -1 | 1 |
| -1 | 0,4 | 0,1 |
| 1 | 0,2 | 0,3 |
Задача 9
Найдите
ковариацию Cov(X,Y) для случайного дискретного вектора (X,Y),
распределенного по закону:
| X=-3 | X=0 | X=1 | |
| Y=-2 | 0,3 | ? | 0,1 |
| Y=1 | 0,1 | 0,1 | 0,2 |
Задача 10
Совместный
закон распределения пары
задан таблицей:
| xh | -1 | 0 | 1 |
| -1 | 1/12 | 1/4 | 1/6 |
| 1 | 1/4 | 1/12 | 1/6 |
Найти
закон распределения вероятностей случайной величины xh и вычислить cov(2x-3h,x+2h).
Исследовать вопрос о зависимости случайных величин x и h.
Задача 11
Составить двумерный закон распределения случайной
величины (X,Y), если известны законы независимых составляющих. Чему равен коэффициент
корреляции rxy?
| X | 20 | 25 | 30 | 35 |
| P | 0.1 | 0.1 | 0.4 | 0.4 |
и
Задача 12
Задано
распределение вероятностей дискретной двумерной случайной величины (X,Y):
| XY | 0 | 1 | 2 |
| -1 | ? | 0,1 | 0,2 |
| 1 | 0,1 | 0,2 | 0,3 |
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Задача 13
Совместное
распределение двух дискретных случайных величин ξ и η задано таблицей:
| ξη | -1 | 1 | 2 |
| 0 | 1/7 | 2/7 | 1/7 |
| 1 | 1/7 | 1/7 | 1/7 |
Вычислить
ковариацию cov(ξ-η,η+5ξ). Зависимы ли ξ и η?
Задача 14
Рассчитать
коэффициенты ковариации и корреляции на основе заданного закона распределения
двумерной случайной величины и сделать выводы о тесноте связи между X и Y.
| XY | 2,3 | 2,9 | 3,1 | 3,4 |
| 0,2 | 0,15 | 0,15 | 0 | 0 |
| 2,8 | 0 | 0,25 | 0,05 | 0,01 |
| 3,3 | 0 | 0,09 | 0,2 | 0,1 |
Задача 15
Задан
закон распределения случайного вектора (ξ,η). Найдите ковариацию (ξ,η)
и коэффициент корреляции случайных величин.
| xy | 1 | 4 |
| -10 | 0,1 | 0,2 |
| 0 | 0,3 | 0,1 |
| 20 | 0,2 | 0,1 |
Задача 16
Для
случайных величин, совместное распределение которых задано таблицей
распределения. Найти:
а) законы
распределения ее компонент и их числовые характеристики;
b) условные законы распределения СВ X при условии Y=b и СВ Y при
условии X=a, где a и b – наименьшие значения X и Y.
с)
ковариацию и коэффициент корреляции случайных величин X и Y;
d) составить матрицу ковариаций и матрицу корреляций;
e) вероятность попадания в область, ограниченную линиями y=16-x2 и y=0.
f) установить, являются ли случайные величины X и Y зависимыми;
коррелированными.
| XY | -1 | 0 | 1 | 2 |
| -1 | 0 | 1/6 | 0 | 1/12 |
| 0 | 1/18 | 1/9 | 1/12 | 1/9 |
| 2 | 1/6 | 0 | 1/9 | 1/9 |
Задача 17
Совместный
закон распределения случайных величин X и Y задан таблицей:
|
XY |
0 |
1 |
3 |
|
0 |
0,15 |
0,05 |
0,3 |
|
-1 |
0 |
0,15 |
0,1 |
|
-2 |
0,15 |
0 |
0,1 |
Найдите:
а) закон
распределения случайной величины X и закон распределения
случайной величины Y;
б) EX, EY, DX, DY, cov(2X+3Y, X-Y), а
также математическое ожидание и дисперсию случайной величины V=6X-8Y+3.
Задача 18
Известен
закон распределения двумерной случайной величины (X,Y).
а) найти
законы распределения составляющих и их числовые характеристики (M[X],D[X],M[Y],D[Y]);
б)
составить условные законы распределения составляющих и вычислить
соответствующие мат. ожидания;
в)
построить поле распределения и линию регрессии Y по X и X по Y;
г)
вычислить корреляционный момент (коэффициент ковариации) μxy и
коэффициент корреляции rxy.
|
|
5 | 20 | 35 |
| 100 | — | — | 0.05 |
| 115 | — | 0.2 | 0.15 |
| 130 | 0.15 | 0.35 | — |
| 145 | 0.1 | — | —- |
Все курсы > Оптимизация > Занятие 3
Как мы уже говорили, исследуя изменения случайных величин, мы зачастую обнаруживаем, что между этими изменениями существует взаимосвязь (bivariate relationship, association).
Откроем ноутбук к этому занятию⧉
Возьмем вот такой простой набор данных.
|
toy_df = pd.DataFrame({ ‘a’:[1, 4, 5, 6, 9], ‘b’:[2, 3, 5, 6, 8], ‘c’:[6, 5, 4, 3, 2], ‘d’:[7, 4, 3, 4, 6] }) toy_df |
Посмотрим на распределения величин с помощью boxplot.
|
plt.figure(figsize = (8, 6)) sns.boxplot(data = toy_df) plt.show() |
Очевидно, распределения отличаются друг от друга, однако пока что мы мало можем сказать об этих распределениях или их взаимосвязи.
Начнем с расчета дисперсии.
Дисперсия
Дисперсия (variance) показывает изменение переменной относительно среднего значения. Приведем формулу для расчета дисперсии генеральной совокупности.
$$ sigma^2 = frac{sum (x_i-mu)^2}{N} $$
где $mu$ — среднее генеральной совокупности из $ x_i $ элементов, а $N$ — ее размер. Дисперсию выборки мы рассчитываем немного иначе.
$$ s^2 = frac{sum (x_i-bar{x})^2}{n-1} $$
В данном случае деление на $n-1$, а не на $n$ называется поправкой Бесселя (Bessel’s correction). Зачем нужна такая поправка? Оказывается, можно показать, что сумма квадратов расстояний, то есть числитель формулы, до среднего генсовокупности (population mean) будет всегда больше, чем сумма квадратов расстояний до выборочного среднего (sample mean).
Как следствие, если при расчете выборочной дисперсии делить на $n$, то мы будем постоянно недооценивать дисперсию генсовокупности. Поправка с делением на $ n-1 $ увеличит дисперсию выборки и сделает ее несмещенной оценкой (unbiased estimation) дисперсии генеральной совокупности.
Приведем основные выводы для показателя дисперсии.
- Большая дисперсия показывает, что значения далеки от среднего и далеки друг от друга
- Дисперсия не может быть отрицательной
- Нулевая дисперсия означает, что все элементы выборки или генеральной совокупности идентичны
Замечу, что далее мы в большинстве случаев будем приводить формулы и вычислять именно выборочные показатели.
Найдем дисперсию для переменной a.
|
# применим формулу дисперсии к первому столбцу (np.square(toy_df[‘a’] — toy_df[‘a’].mean())).sum() / (toy_df.shape[0] — 1) |
Дисперсию для каждой переменной можно измерить с помощью функции np.var() библиотеки Numpy.
|
# рассчитаем дисперсию по столбцам с делением на n — 1 np.var(toy_df, ddof = 1) |
|
a 8.5 b 5.7 c 2.5 d 2.7 dtype: float64 |
Точно такой же результат можно получить с помощью метода .var() библиотеки Pandas.
|
# ddof = 1 можно не указывать, это параметр по умолчанию toy_df.var() |
|
a 8.5 b 5.7 c 2.5 d 2.7 dtype: float64 |
Параметр ddof означает Delta Degrees of Freedom (дельта степеней свободы) и указывает на размер поправки при расчете дисперсии выборки. Соответственно ddof = 1 как раз использует деление на $n-ddof = n-1$. Как мы видим, дисперсия переменной a существенно больше, чем, например, переменной d.
Показатель дисперсии представляет собой квадрат измеряемых нами величин. Для понимания величины отклонения это не очень удобно. В этом смысле лучше подойдет среднее квадратическое отклонение.
Среднее квадратическое отклонение
Среднее квадратическое отклонение (СКО, standard deviation) как раз вычисляется как корень из дисперсии.
$$ sigma = sqrt{sigma^2} $$
$$ s = sqrt{s^2} $$
Рассчитаем СКО для первого столбца.
|
np.sqrt((np.square(toy_df[‘a’] — toy_df[‘a’].mean())).sum() / (toy_df.shape[0] — 1)) |
Мы также можем использовать функцию np.std() библиотеки Numpy и метод .std() библиотеки Pandas.
|
# для расчета СКО будем также делить на n — 1 np.std(toy_df, ddof = 1) |
|
a 2.915476 b 2.387467 c 1.581139 d 1.643168 dtype: float64 |
|
# опять же, этот параметр установлен по умолчанию, и его можно не указывать toy_df.std() |
|
a 2.915476 b 2.387467 c 1.581139 d 1.643168 dtype: float64 |
Теперь перейдем к изучению взаимосвязи между переменными. Одним из способов измерения взаимосвязи является ковариация.
Ковариация
Ковариация (covariance) измеряет направление изменения двух переменных. Другими словами она позволяет понять как изменится одна из двух переменных при изменении второй.
Построим три точечные диаграммы (scatter plots) для переменных a и b, b и c, и c и d соответственно.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
# создадим сетку 1 х 3 с подграфиками для каждой из пар переменных f, (pair1, pair2, pair3) = plt.subplots(nrows = 1, ncols = 3, figsize = (12, 4), constrained_layout = True) # в первый подграфик поместим точечную диаграмму переменных a и b pair1.scatter(toy_df[‘a’], toy_df[‘b’]) pair1.set_title(‘a vs. b’, fontsize = 14) pair1.set(xlabel = ‘a’) pair1.set(ylabel = ‘b’) # во второй — b и c pair2.scatter(toy_df[‘b’], toy_df[‘c’]) pair2.set_title(‘b vs. c’, fontsize = 14) pair2.set(xlabel = ‘b’) pair2.set(ylabel = ‘c’) # в третий — c и d pair3.scatter(toy_df[‘c’], toy_df[‘d’]) pair3.set_title(‘c vs. d’, fontsize = 14) pair3.set(xlabel = ‘c’) pair3.set(ylabel = ‘d’) plt.show() |
На первом и втором графике мы видим линейную взаимосвязь. Приведем формулу для ее измерения.
$$ Cov_{x, y} = frac{sum (x_i-bar{x})(y_i-bar{y})}{n-1} $$
Как вы видите, ковариация представляет собой сумму произведений отклонений переменных от своего среднего значения, усредненную на количество наблюдений ($n-1$).
Рассчитаем ковариацию a и b с помощью Питона.
|
((toy_df[‘a’] — toy_df[‘a’].mean()) * (toy_df[‘b’] — toy_df[‘b’].mean())).sum() / (toy_df.shape[0] — 1) |
Если использовать функцию np.cov() библиотеки Numpy или метод .cov() библиотеки Pandas, то мы получим так называемую ковариационную матрицу (covariance matrix).
|
# для расчета по столбцам нужно использовать параметр rowvar = False np.cov(toy_df, ddof = 1, rowvar = False) |
|
array([[ 8.5 , 6.75, -4.5 , -1. ], [ 6.75, 5.7 , -3.75, -0.55], [-4.5 , -3.75, 2.5 , 0.5 ], [-1. , -0.55, 0.5 , 2.7 ]]) |
По диагонали указана дисперсия, вне диагонали — ковариация любых двух переменных.
Переменные a и b имеют положительную ковариацию, с увеличением a увеличивается и b. Переменные b и c — отрицательную, переменные c и d демонстрируют нулевую или близкую к нулевой ковариацию.
Интересно, что если переменные независимы (между ними нет взаимосвязи) — ковариация будет равна нулю, при этом обратное не обязательно верно. Если ковариация равна нулю, взаимосвязь может быть, просто она нелинейна (возможно именно такая взаимосвязь существует между c и d).
Недостатком ковариации является то, что она измеряет только направление, но не силу взаимосвязи. Если мы умножим значения обеих переменных, например, на три, то ковариация, исходя из формулы выше, увеличится в девять раз (поскольку как x, так и y каждой пары переменных умножаются на три), при этом очевидно сила взаимосвязи никак не изменится.
|
# умножим данные на три, рассчитаем ковариацию # и разделим на ковариационную матрицу исходного датасета, # чтобы посмотреть масштаб изменения (toy_df * 3).cov() / toy_df.cov() |
Этот недостаток исправляет коэффициент корреляции.
Корреляция
Корреляция (correlation) между двумя переменными (случайными величинами) измеряет не только направление, но и силу взаимосвязи.
Параметрические и непараметрические тесты
Прежде чем перейти к различным коэффициентам корреляции несколько слов про разделение статистических тестов или методов на параметрические и непараметрические.
Параметрические методы (parametric methods) основываются на допущении (assumption) или предпосылке о том, как распределена генеральная совокупность, из которой взята изучаемая выборка. Например, статистический тест может предполагать, что данные имеют нормальное распределение.
Непараметрические методы (non-parametric) таких допущений соответственно не предполагают.
На практике это означает, что если допущения параметрического теста не выполняются, его результат нельзя считать достоверным. Для непараметрического теста такое ограничение отсутствует.
Коэффициент корреляции Пирсона
Коэффициент корреляции Пирсона (Pearson correlation coefficient) — это параметрический тест, который строится на основе расчета ковариации двух переменных, разделенного на произведение СКО каждой из них.
$$ r_{pearson} = frac{Cov_{x, y}}{s_x s_y} $$
Деление на произведение СКО $(s_x s_y)$ выражает любой коэффициент ковариации в единицах этого произведения (нормализует его). Как следствие, мы получаем возможность сравнения коэффициентов корреляции, а значит измерения не только направления, но и силы взаимосвязи.
Коэффициент корреляции всегда находится в диапазоне от $-1$ до $1$.
Значения, приближающиеся к 1 указывают на сильную положительную линейную корреляцию. Близкие к −1 — на сильную отрицательную линейную корреляцию. Околонулевые значения означают отсутствие линейной корреляции.
Посмотрим на график возможных вариантов корреляции данных, приведенный на занятии вводного курса.
Библиотека Numpy предлагает нам функцию np.corrcoef() для создания корреляционной матрицы (correlation matrix) коэффициента Пирсона.
|
# для расчета корреляции по столбцам используем параметр rowvar = False np.corrcoef(toy_df, rowvar = False).round(2) |
|
array([[ 1. , 0.97, -0.98, -0.21], [ 0.97, 1. , -0.99, -0.14], [-0.98, -0.99, 1. , 0.19], [-0.21, -0.14, 0.19, 1. ]]) |
В Pandas мы можем воспользоваться методом .corr().
|
# параметр method = ‘pearson’ используется по умолчанию, # его можно не указывать toy_df.corr(method = ‘pearson’).round(2) |
Корреляция переменной с самой собой равна единице, что и отражают значения на главной диагонали матрицы. Кроме того, очевидно, что величина X также коррелирует с Y, как Y c X.
Продемонстрируем также, что изменение масштаба данных не отразится на коэффициенте корреляции.
|
# умножим значения датасета на два и снова рассчитаем коэффициент Пирсона (toy_df * 2).corr().round(2) |
Особенности коэффициента Пирсона
Несколько важных замечаний.
Замечание 1. Ни ковариация, ни корреляция не устанавливают причинно-следственной связи (correlation does not imply causation). Например, мы можем наблюдать существенную корреляцию между потреблением мороженого и продажами кондиционеров, при этом изменения в обеих переменных могут быть вызваны третьей, на рассматриваемой нами переменной, в частности, температурой воздуха.
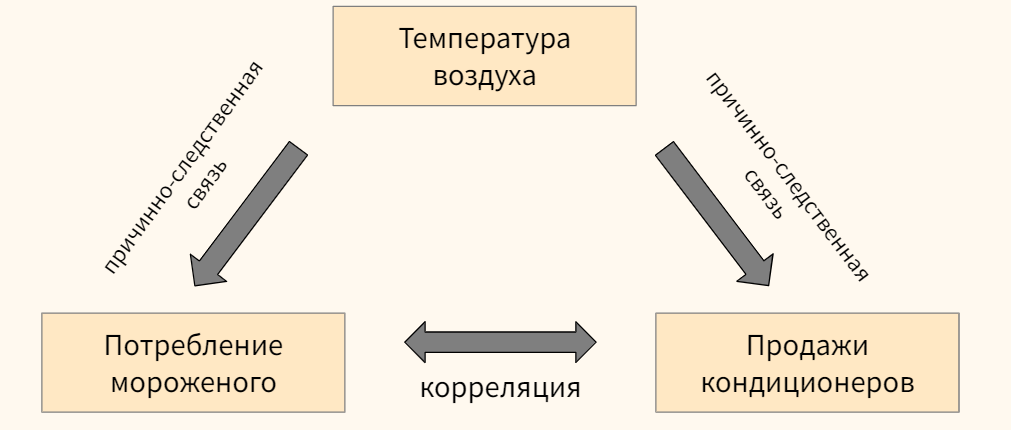
Кроме того в некоторых случаях корреляция может быть чистой случайностью.
Замечание 2. Коэффициент корреляции Пирсона измеряет взаимосвязь (1) количественных переменных и (2) предполагает, что обе переменные имеют нормальное распределение (это и есть упомянутое выше допущение (assumption) параметрического теста).
Замечание 3. Как и в случае с ковариацией, отсутствие линейной корреляции не означает отсутствие взаимосвязи. Возможно взаимосвязь есть, но она нелинейна.
Замечание 4. Более того, на коэффициент корреляции существенное влияние оказывают выбросы (outliers).
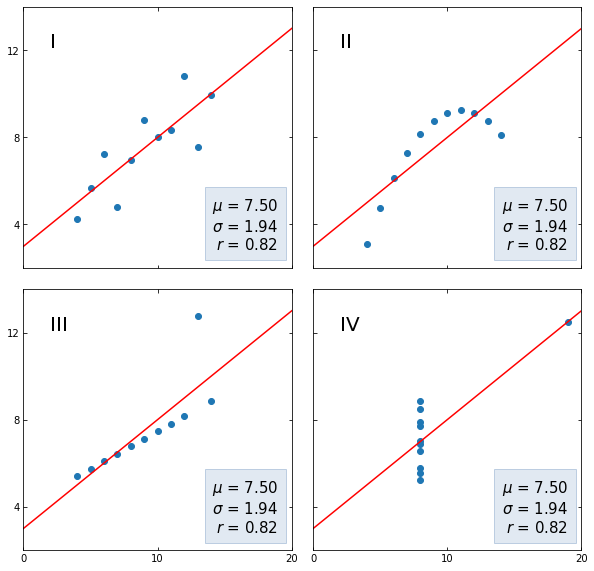
Последние два замечения хорошо иллюстрируются квартетом Энскомба (Anscombe’s quartet), набором небольших датасетов (кстати, встроенных в сессионное хранилище Google Colab) с совершенно разными распределениями x и y, но одинаковым средним арифметическим и СКО переменной y, а также одинаковым коэффициентом корреляции Пирсона.
Вначале получим необходимые данные.
|
# загрузим данные в формате json из сессионного хранилища, # преобразуем в датафрейм и посмотрим на первые три строки anscombe = pd.read_json(‘/content/sample_data/anscombe.json’) anscombe.head(3) |
|
# разобьем данные на четыре части по столбцу Series series_by_group = [x for _, x in anscombe.groupby(‘Series’)] # отдельно получим названия каждой из четырех частей labels = anscombe.Series.unique() labels |
|
array([‘I’, ‘II’, ‘III’, ‘IV’], dtype=object) |
|
# создадим пустой словарь datasets = {} # в цикле пройдемся по названиям и значениям переменных x и y каждой из частей for label, series in zip(labels, series_by_group): # каждое название части станет ключом словаря, а переменные x и y — значениями datasets[label] = (list(series.X.round(2)), list(series.Y.round(2))) # выведем содержимое словаря с помощью функции pprint() from pprint import pprint pprint(datasets) |
|
{‘I’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.81, 5.68]), ‘II’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [9.14, 8.14, 8.74, 8.77, 9.26, 8.1, 6.13, 3.1, 9.13, 7.26, 4.74]), ‘III’: ([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5], [7.46, 6.77, 12.74, 7.11, 7.81, 8.84, 6.08, 5.39, 8.15, 6.42, 5.73]), ‘IV’: ([8, 8, 8, 8, 8, 8, 8, 19, 8, 8, 8], [6.58, 5.76, 7.71, 8.84, 8.47, 7.04, 5.25, 12.5, 5.56, 7.91, 6.89])} |
Теперь выведем каждый из четырех датасетов на графиках.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 |
# создадим сетку подграфиков 2 х 2 fig, axs = plt.subplots(2, 2, sharex = True, sharey = True, figsize = (10, 10), gridspec_kw = {‘wspace’: 0.08, ‘hspace’: 0.08}) # определим границы осей и отметки на осях x и y axs[0, 0].set(xlim = (0, 20), ylim = (2, 14)) axs[0, 0].set(xticks = (0, 10, 20), yticks = (4, 8, 12)) # пройдемся по подграфикам, а также ключам и значениям словаря datasets for ax, (label, (x, y)) in zip(axs.flat, datasets.items()): # выведем название (номер) группы ax.text(0.1, 0.9, label, fontsize = 20, transform = ax.transAxes, va = ‘top’) ax.tick_params(direction = ‘in’, top = True, right = True) # построим точечные диаграммы ax.scatter(x, y) # обучим модель линейной регрессии slope, intercept = np.polyfit(x, y, deg = 1) # выведем график линейной регрессии x_vals = np.linspace(0, 20, num = 1000) y_vals = intercept + slope * x_vals ax.plot(x_vals, y_vals, ‘r’) # рассчитаем среднее арифметическое, СКО и корреляцию Пирсона stats = (f‘$\mu$ = {np.mean(y):.2f}n’ f‘$\sigma$ = {np.std(y):.2f}n’ f‘$r$ = {np.corrcoef(x, y)[0][1]:.2f}’) # создадим отформатированное пространство на графике bbox = dict(boxstyle = ‘square’, pad = 0.5, fc = ‘#c5d4e6’, ec = ‘#89a8cc’, alpha = 0.5) # и выведем в нем рассчитанные выше статистические показатели ax.text(0.95, 0.07, stats, fontsize = 15, bbox = bbox, transform = ax.transAxes, horizontalalignment = ‘right’) plt.show() |
- Как мы видим, на первом графике прослеживается линейная корреляция без каких-либо сюрпризов;
- Во втором наборе данных у нас нелинейная зависимость, силу которой мы не смогли отразить с помощью коэффициента Пирсона;
- В третьем наборе коэффициент корреляции находится под сильным влиянием выброса;
- В четвертом, корреляция по сути отсутствует и тем не менее одного наблюдения оказывается достаточно для появления достаточно сильной корреляции.
Помимо ограничений коэффициента корреляции, эти наборы данных демонстрируют в целом важность визуальной оценки данных.
Коэффициент Пирсона как скалярное произведение векторов
Распишем формулу корреляции более подробно (см. формулы ковариации, дисперсии и СКО).
$$ r_{pearson} = frac{ frac{sum (x_i-bar{x})(y_i-bar{y})}{n-1} }{ sqrt {frac{sum (x_i-bar{x})^2}{n-1} frac{sum (y_i-bar{y})^2}{n-1} } } $$
Упростим выражение.
$$ r_{pearson} = frac{ sum (x_i-bar{x})(y_i-bar{y}) } { sqrt {sum (x_i-bar{x})^2} sqrt{ sum (y_i-bar{y})^2 } } $$
Теперь давайте представим случайные величины X и Y в форме векторов
$$ textbf{x} = [x_1, x_2, x_3,…, x_n] $$
$$ textbf{y} = [y_1, y_2, y_3,…, y_n] $$
со средними значениями $ bar{x} $ и $ bar{y} $. Затем определим новые векторы $ textbf{x}^c $ и $ textbf{y}^c $, в которых из значений $x_i$ и $y_i$ вычтем соответствующие средние значения.
$$ textbf{x}^c = [x_1-bar{x}, x_2-bar{x}, x_3-bar{x},…, x_n-bar{x}] $$
$$ textbf{y}^c = [y_1-bar{x}, y_2-bar{x}, y_3-bar{y},…, y_n-bar{y}] $$
Обратим внимание, что (1) числитель (1) в формуле коэффициента корреляции представляет собой покомпонентное умножение векторов с последующим сложением произведений (то есть скалярное произведение).
Знаменатель (2) же представляет собой покомпонентное умножение и сложение произведений векторов самих на себя. Как мы узнаем на курсе линейной алгебры, корень из скалярного произведение вектора на самого себя есть длина этого вектора. Приведем пример для вектора $ textbf{x} $
$$ sqrt { textbf{x}^2 } = sqrt { textbf{x} cdot textbf{x} } = || textbf{x} || $$
Исходя из этих двух соображений, перепишем формулу расчета коэффициента Пирсона.
$$ r_{pearson} = frac { textbf{x}^c cdot textbf{y}^c }{|| textbf{x}^c || cdot || textbf{y}^c || } $$
Это формула косинусного сходства двух векторов. Другими словами, коэффициент корреляции равен косинусу угла между двумя векторами данных. Рассчитаем корреляцию через косинусное сходство с помощью Питона.
|
# возьмем данные первой группы квартета Энскомба x = np.array([10, 8, 13, 9, 11, 14, 6, 4, 12, 7, 5]) y = np.array([8.04, 6.95, 7.58, 8.81, 8.33, 9.96, 7.24, 4.26, 10.84, 4.81, 5.68]) # вычтем из каждого значения x и y соответствующее среднее арифметическое xc = x — np.mean(x) yc = y — np.mean(y) # используем формулу косинусного сходства и округлим результат np.round(np.dot(xc, yc)/(np.linalg.norm(xc) * np.linalg.norm(yc)), 2) |
Как уже было сказано, у коэффициента Пирсона есть ряд ограничений, в частности, он выявляет только линейную взаимосвязь количественных переменных. В этой связи рассмотрим коэффициент Спирмена.
Коэффициент ранговой корреляции Спирмена
Коэффициент ранговой корреляции Спирмена (Spearman’s Rank Correlation Coefficient) хорошо измеряет постоянно возрастающую или постоянно убывающую (монотонную) зависимость двух переменных, а также подходит для работы с категориальными порядковыми данными.
Это непараметрический тест, который не предполагает каких-либо допущений о распределении генеральной совокупности.
Монотонная зависимость
Напомню, что функция или зависимость называется монотонной (monotonic), если на заданном интервале ее производная (градиент) не меняет знака (то есть всегда имеет неотрицательное или неположительное значение). Приведем пример.

Рассмотрим взаимосвязь площади (area) и цены (price) квартиры.
|
# поместим данные площади и цены квартиры в датафрейм flats = pd.DataFrame({ ‘area’ :[78, 90, 74, 69, 63, 57, 72, 67, 83], ‘price’ :[9.1, 9.0, 8.9, 8.2, 6.0, 5.8, 8.7, 7.5, 9.2] }) flats |
Выведем эти данные с помощью точечной диаграммы (scatter plot).
|
plt.figure(figsize = (8, 6)) plt.scatter(flats.area, flats.price) plt.xlabel(‘Площадь, кв. м.’, fontsize = 15) plt.ylabel(‘Цена, млн. руб.’, fontsize = 15) plt.grid() plt.show() |
Рассчитаем коэффициент корреляции Пирсона.
|
# применим метод .corr() с параметром method = ‘pearson’ # выведем одно из значений корреляционной матрицы с помощью .iloc[0, 1] и округлим результат flats.corr(method = ‘pearson’).iloc[0, 1].round(2) |
Достаточно высокий уровень корреляции. При этом, как мы видим, зависимость нелинейна и возможно коэффициент Пирсона не до конца уловил силу взаимосвязи. Как нам преодолеть ограничение линейности?
Обратите внимание, прежде чем построить график, Питон упорядочил значения площади (ось x). Упорядочил, то есть присвоил им ранг (порядковый номер) от первого до, в данном примере, девятого. В каком случае значения цены (ось y) будут также возрастать? Только в случае если их ранги мало отличаются от рангов значений площади квартиры.
Коэффициент корреляции Спирмена как раз считает степень отличия рангов двух переменных.
Приведем формулу.
$$ r_{spearman} = frac{6 sum d_i^2 }{n(n^{2}-1)} $$
Вычислим коэффициент Спирмена с помощью Питона. Вначале присвоим каждому значению в обоих столбцах ранг (порядковый номер), предварительно упорядочив значения по убыванию.
|
# для этого используем метод .rank() с параметром ascending = False flats[‘area_rank’] = flats.area.rank(ascending = False) flats[‘price_rank’] = flats.price.rank(ascending = False) flats |
Таким образом площади дома в 90 квадратных метров и цене в 9,2 миллона рублей будет присвоен ранг 1. Теперь мы можем вычислить разницу рангов для каждого из наблюдений и возвести ее в квадрат.
|
# вычтем из рангов площади ранги цены flats[‘diff’] = flats[‘area_rank’] — flats[‘price_rank’] # возведем разницу в квадрат flats[‘diff_sq’] = np.square(flats[‘diff’]) flats |
Выполним оставшиеся вычисления в соответствии с приведенной выше формулой.
|
# поместим количество наблюдений в переменную n n = flats.shape[0] # применим формулу для расчета коэффициента Спирмена 1 — ((6 * flats[‘diff_sq’].sum()) / (n * (n**2 — 1))) |
Рассчитаем корреляцию Спирмена с помощью метода .corr() библиотеки Pandas с параметром method = ‘spearman’.
|
flats[[‘area’, ‘price’]].corr(method = ‘spearman’).iloc[0, 1].round(2) |
Как мы видим, этот коэффициент гораздо лучше уловил монотонную нелинейную зависимость двух переменных.
Также замечу, что коэффициент корреляции Спирмена менее чувствителен к выбросам, находящимся на «краях» обеих выборок, потому что опять же учитывает не само значение, а присвоенный ему ранг.
Категориальные порядковые данные
Как уже было сказано, помимо количественных значений коэффициент Спирмена способен измерить направление и силу взаимосвязи категориальных порядковых значений (categorical ordinal data).
Это могут быть оценки уровня удовлетворености клиента (очень понравилось, понравилось, не понравилось), размеры, выраженные категорией (S, M, L, …) и так далее.
В качестве примера рассмотрим оценку собственного самочувствия по шкале от 1 до 10, которую пациенты поставили себе до и после нового метода лечения.
|
# создадим датафрейм с данными о самочувствии treatment = pd.DataFrame( [ [3, 2], [4, 3], [2, 1], [1, 5], [6, 7], [7, 6], [5, 4] ], columns = [‘Before’, ‘After’]) treatment |
|
# выведем данные на графике plt.figure(figsize = (8, 6)) plt.scatter(treatment.Before, treatment.After) plt.xlabel(‘Before’, fontsize = 15) plt.ylabel(‘After’, fontsize = 15) plt.grid() plt.show() |
По всей видимости корреляция должна быть меньше, чем в предыдущем примере. Приступим к измерениям. Сделать это на самом деле очень просто, потому что порядковые значения уже сами по себе представляют собой ранги. Остается только найти квадрат их разности и применить формулу коэффициента корреляции.
|
# найдем квардрат разницы рангов treatment[‘diff’] = treatment[‘Before’] — treatment[‘After’] treatment[‘diff_sq’] = np.square(treatment[‘diff’]) treatment |
|
# применим формулу коэффициента корреляции Спирмена n = treatment.shape[0] round(1 — ((6 * treatment[‘diff_sq’].sum()) / (n * (n**2 — 1))), 2) |
Остается сравнить с методом .corr() библиотеки Pandas.
|
treatment[[‘Before’, ‘After’]].corr(method = ‘spearman’).iloc[0, 1].round(2) |
Обратите внимание, ни в количественных данных, ни в порядковых у нас не было повторяющихся или совпадающих наблюдений. В случае совпадающих наблюдений (tied ranks), то есть когда значения x или y повторяются, расчет коэффициента корреляции Спирмена также возможен, но немного усложняется.
Коэффициент ранговой корреляции Кендалла
Коэффициент ранговой корреляции Кендалла (еще говорят тау Кендалла или тау-коэффициент, Kendall’s $tau$ rank correlation coefficient), как и метод Спирмена, может применяться для измерения силы взаимосвязи количественных и порядковых категориальных переменных и подходит для анализа нелинейных зависимостей. Это также непараметрический тест.
Смысл и методику расчета коэффициента Кендалла легко понять на примере. Вновь возьмем данные о самочувствии до и после лечения.
|
# вернем датафрейм к исходному виду treatment = treatment[[‘Before’, ‘After’]] treatment |
Теперь рассмотрим две пары наблюдений, например, под индексом 0 и 1.
Мы видим, что в столбце Before значения наблюдения 0 меньше, чем значение наблюдения 1 (потому что 3 < 4). То же самое можно наблюдать в столбце After (2 < 3). Такая пара наблюдений называется конкордантной (concordant). Конкордантной будет и пара наблюдений, где оба значения в первом наблюдении больше обоих значений во втором. К ним относятся, например, пары 1 и 2 (где 4 > 2, а 3 > 1).
Если же описанные выше условия не выполняются, то такая пара наблюдений будет называться дискордантной (discordant). К таким наблюдениям относятся, например, наблюдения 4 и 5 (6 > 7, но 7 < 6).
Отнесем каждую из пар нашего датасета к одному из этих классов.
|
# 0 # 1 C # 2 C C # 3 D D D # 4 C C C C # 5 C C C C D # 6 C C C D C C # 0 1 2 3 4 5 6 |
Получилось 16 конкордантных (C) и 5 дискордантных (D) пар. Их общее количество очевидно равно 21. Это значение удобно посчитать по формуле сочетаний.
$$ C(n, r) = frac{n!}{(n-r)! r!} rightarrow C(7, 2) = frac{7!}{(7-2)! 2!} = 21 $$
где n — количество наблюдений, а r равно двум, потому что мы ищем сочетания пар элементов. Можно воспользоваться и упрощенной формулой.
$$ C(r) = frac{(n cdot (n-1))}{2} rightarrow C(7) = frac{7 cdot (7-1)}{2} = 21 $$
|
# найдем количество парных сочетаний с помощью Питона n = 7 pairs = (7 * (7 — 1)) // 2 pairs |
Так вот, коэффициент корреляции Кендалла показывает соотношение конкордантных и дискордантных пар по следующей формуле.
$$ tau = frac{text{concordant pairs}-text{discordant pairs}}{text{total pairs}}$$
Применим ее к нашему датасету.
|
concordant = 16 discordant = pairs — concordant np.round((concordant — discordant) / pairs, 2) |
Точно такого же результата можно добиться с помощью метода .corr() библиотеки Pandas.
|
treatment.corr(method = ‘kendall’).iloc[0, 1].round(2) |
Смысл этого коэффициента в следующем.
Чем больше доля конкордантных пар, тем больше схожих рангов, а значит сильнее взаимосвязь между переменными.
Коэффициент неопределенности
Определение и понятие симметричности теста
Коэффициент неопределенности (uncertainty coefficient) или U Тиля (Theil’s U) позволяет оценить взаимосвязь между двумя категориальными признаками, например, X и Y. Формально он определяется как значение X при условии данного Y.
$$U(x|y)$$
Более того, в отличие от некоторых других тестов, он несимметричен (asymmetric), что позволяет узнать зависит ли Y от X, так же как X от Y.
$$U(y|x) neq U(x|y)$$
Понятие симметричности теста легко представить на следующем простом примере.

Очевидно, что мы легко можем предсказать Y зная X, а вот зная Y мы можем меньше сказать про X (обратите внимание, что категории в X не совпадают для двух категорий в Y).
Используем этот несложный датасет для дальнейших расчетов.
|
# возьмем две категориальные переменные со следующими значениями x = np.array([‘q’, ‘t’, ‘q’, ‘n’, ‘n’, ‘c’]) y = np.array([‘A’, ‘A’, ‘A’, ‘B’, ‘B’, ‘B’]) |
Как рассчитывается
Условная энтропия
U Тиля основывается на понятии условной энтропии (condition entropy), которая позволяет измерить объем информации, необходимый для описания значений переменной X с помощью переменной Y.
$$ S(X|Y) = -sum p(x,y) logfrac{p(x,y)}{p(y)} $$
Теоретическое обоснование формул условной энтропии и энтропии выходит за рамки сегодняшнего занятия. Мы сосредоточимся на расчете и практическом применении каждой из них.
Рассчитаем условную энтропию с помощью Питона. Вначале нам необходимо рассчитать частоту классов категориальных переменных. Для этого прекрасно подойдет класс Counter модуля collections.
|
# импортируем класс Counter модуля collections from collections import Counter |
Посмотрим, сколько раз встречаются классы переменной Y.
|
# найдем частоту классов переменной y y_counts = Counter(y) y_counts |
|
Counter({‘A’: 3, ‘B’: 3}) |
Далее возьмем каждую пару значений X и Y и рассчитаем, сколько раз встречается каждая из них.
|
# возьмем каждую пару значений X и Y с помощью функций zip() и list() list(zip(x, y)) |
|
[(‘q’, ‘A’), (‘t’, ‘A’), (‘q’, ‘A’), (‘n’, ‘B’), (‘n’, ‘B’), (‘c’, ‘B’)] |
|
# рассчитаем их частоту xy_counts = Counter(list(zip(x, y))) xy_counts |
|
Counter({(‘A’, ‘q’): 2, (‘A’, ‘t’): 1, (‘B’, ‘n’): 2, (‘B’, ‘c’): 1}) |
Теперь найдем общее количество значений.
|
total_counts = len(x) total_counts |
В соответствии с формулой выше нам нужно найти вероятность Y ($p(y)$) и вероятность X при условии Y ($p(x,y)$). Для расчета $p(y)$ мы пройдемся по ключам словаря xy_counts и посмотрим в словаре y_counts сколько раз встречается второй элемент каждого ключа.
|
# пройдемся по ключам xy_counts for xy in xy_counts.keys(): # (выведем ключ для наглядности) print(xy) # и посмотрим в y_counts сколько раз встречается второй элемент каждого кортежа print(y_counts[xy[1]]) |
|
(‘q’, ‘A’) 3 (‘t’, ‘A’) 3 (‘n’, ‘B’) 3 (‘c’, ‘B’) 3 |
Мы видим, что категория A и категория B в нашем случае встречаются по три раза. Остается разделить частоту каждой категории на общее количество элементов.
|
# найдем p(y) разделив каждую частоту на общее количество элементов for xy in xy_counts.keys(): print(y_counts[xy[1]] / total_counts) |
Выполним похожее упражнение для того, чтобы найти $p(x,y)$.
|
# снова пройдемся по парам значений for xy in xy_counts.keys(): # (выведем эти пары для наглядности) print(xy) # выведем частоту каждой пары (на этот раз именно пары, а нее ее второго элемента) print(xy_counts[xy]) # и рассчитаем вероятность print(xy_counts[xy] / total_counts) |
|
(‘q’, ‘A’) 2 0.3333333333333333 (‘t’, ‘A’) 1 0.16666666666666666 (‘n’, ‘B’) 2 0.3333333333333333 (‘c’, ‘B’) 1 0.16666666666666666 |
|
# для дальнейшей работы нам понадобится модуль math import math |
Теперь остается подставить $p(y)$ и $p(x,y)$ в формулу.
|
# объявим переменную для условной энтропии cond_entropy = 0.0 # в цикле снова пройдемся по парам значений for xy in xy_counts.keys(): # найдем p(y) p_y = y_counts[xy[1]] / total_counts # и p(x,y) p_xy = xy_counts[xy] / total_counts # подставим их в формулу и просуммируем результат # (мы использовали логарифм с основанием два, но можно использовать, например, и натуральный логарифм) cond_entropy += p_xy * math.log(p_y / p_xy, 2) cond_entropy |
Поместим этот код в функцию.
|
# поместим код в функцию def conditional_entropy(x, y, log_base: float = 2): y_counts = Counter(y) xy_counts = Counter(list(zip(x, y))) total_counts = len(x) cond_entropy = 0.0 for xy in xy_counts.keys(): p_xy = xy_counts[xy] / total_counts p_y = y_counts[xy[1]] / total_counts cond_entropy += p_xy * math.log(p_y / p_xy, log_base) return cond_entropy |
|
# вновь рассчитаем условную энтропию conditional_entropy(x, y) |
Убедимся в несимметричности объема информации, содержащегося в X относительно Y и в Y относительно X, поменяв переменные местами.
|
conditional_entropy(y, x) |
Здесь становится очевидным важный факт.
Если условная энтропия равна нулю, это значит, что с помощью переменной Y мы можем полностью описать переменную X (в нашем примере наоборот). При этом, чем выше условная энтропия, тем меньше информации об X содержится в переменной Y.
Теперь рассмотрим второй компонент формулы коэффициента неопределенности.
Энтропия
Энтропия (entropy) случайной величины рассчитывается по следующей формуле.
$$ S(X) = -sum p(x)log{p(x)} $$
Это значение тем выше, чем менее вероятным является каждый из исходов испытания. Например, энтропия бросания игральной кости будет выше, чем подбрасывания монеты. В первом случае вероятность каждого исхода равна 1/6, во втором 1/2.
Убедимся в этом с помощью функции entropy() модуля stats библиотеки scipy.
|
# импортируем модуль stats библиотеки scipy import scipy.stats as st # рассчитаем энтропию бросания кости и подбрасывания монеты st.entropy([1/6, 1/6, 1/6, 1/6, 1/6, 1/6], base = 2), st.entropy([1/2, 1/2], base = 2) |
Выполним расчет вручную. Вначале найдем вероятность каждого из значений случайной величины $p(x)$.
|
# найдем частоту каждого элемента в X x_counts = Counter(x) # их общее количество total_counts = len(x) # разделим каждую частоту на общее количество элементов p_x = list(map(lambda n: n / total_counts, x_counts.values())) # выведем результат print(p_x) |
|
[0.3333333333333333, 0.16666666666666666, 0.3333333333333333, 0.16666666666666666] |
Теперь подставим это значение в формулу и найдем энтропию.
|
# объявим переменную для условной энтропии entropy = 0.0 # подставим каждую вероятность в формулу и просуммируем for p in p_x: entropy += —p * math.log(p, 2) # выведем результат entropy |
Проверим правильность результата с помощью функции библиотеки scipy().
|
st.entropy(p_x, base = 2) |
Также объявим соответствующую функцию.
|
# объявим функцию def entropy(x, log_base: float = 2): x_counts = Counter(x) total_counts = len(x) p_x = list(map(lambda n: n / total_counts, x_counts.values())) entropy = 0.0 for p in p_x: entropy += —p * math.log(p, 2) return entropy |
|
# проверим результат entropy(x) |
Замечу, что условная энтропия S(X|Y) равна энтропии случайной величины S(X), если величины X и Y независимы.
$$ S(X|Y) = S (X) iff X ⫫ Y $$
Из этого следует, что самое большее условная энтропия может быть равна энтропии этой переменной (в случае, если Y никак не объясняет X).
$$ S(X) leq S(X|Y) $$
Все это важно для расчета коэффициента неопределенности.
U Тиля
Приведем и обсудим формулу.
$$ U(X|Y) = frac{S(X)-S(X|Y)}{S(X)} $$
Зачем рассчитывать не только условную энтропию, но и энтропию случайной величины? Дело в том, что так мы можем не просто измерять «объяснимость» переменной X с помощью Y, но и сравнивать между собой условную энтропию любых категориальных переменных.
Арифметически, чем ниже условная энтропия, тем ближе значение показателя к единице. Чем она выше, тем коэффициент неопределенности ближе к нулю.
Таким образом, U Тиля всегда находится в диапазоне от 0 до 1. При этом, ноль означает, что переменная Y не несет никакой информации относительно переменной X, единица — что переменная Y содержит всю необходимую информацию.
Рассчитаем U Тиля с помощью Питона.
|
# сразу объявим функцию def ucoef(x, y, log_base = 2): # найдем условную энтропию S(X,Y) s_xy = conditional_entropy(x, y, log_base) # энтропию S(X) s_x = entropy(x, log_base) # подставим эти значения в формулу u = (s_x — s_xy) / s_x # выведем результат return u |
Найдем коэффициент неопределенности для X и Y.
Кроме того, убедимся, что X полностью объясняет Y.
Обратите внимание, что коэффициент не может принимать отрицательных значений. Это логично, потому что строго говоря в случае категориальных переменных мы измеряем не корреляцию (направление и силу взаимного изменения, correlation), а степень взаимосвязи (association) между двумя переменными, которая либо есть (и может доходить до единицы), либо ее нет (равна нулю).
Точечно-бисериальная корреляция
Точечно-бисериальная корреляция (point-biserial correlation) позволяет оценить взаимосвязь между количественной переменной и дихотомической (выраженной двумя значениями) качественной переменной. Например, нам может быть важно оценить связь возраста (X) и выживаемости пассажиров «Титаника» (Y, классы 0 и 1). Приведем формулу.
Формула
$$ r_{pb} = frac{M_1-M_0}{s_n} sqrt{frac{n_1 n_0}{n^2}} $$
В данном случае мы делим наблюдения на две группы, в первую группу попадут наблюдения, относящиеся к классу 0, во вторую — к классу 1. Для каждой группы мы считаем средние значения ($M_0$ и $M_1$) и делим их разность на среднее квадратическое отклонение всех значений в переменной X ($s_n$).
Под корнем находится произведение относительного размера двух групп ($n_0$ и $n_1$ — это размеры групп, $n$ — общее число наблюдений).
Коэффициент точечно-бисериальной корреляции находится в диапазоне от $-1$ до $1$ и интерпретируется так же, как и коэффициент корреляции Пирсона.
Выше приведена формула для генеральной совокупности. Если нам доступна лишь выборка, формула выглядит следующим образом.
$$ r_{pb} = frac{M_1-M_0}{s_{n-1}} sqrt{frac{n_1 n_0}{n(n-1)}} $$
СКО ($s_{n-1}$) в этом случае также рассчитывается по формуле для выборки. Приведем пример.
Пример расчета на Питоне
Подгрузим датасет о вине из библиотеки sklearn. На основе свойств вин нам предлагается спрогнозировать один из трех классов вина (классы 0, 1 и 2). Так как нам нужна дихотомическая переменная, удалим наблюдения, относящиеся к классу 2.
|
# из модуля datasets библиотеки sklearn импортируем датасет о вине from sklearn import datasets data = datasets.load_wine() # превратим его в датафрейм wine = pd.DataFrame(data.data, columns = data.feature_names) # добавим целевую переменную wine[‘target’] = data.target # оставим только классы 0 и 1 wine = wine[wine.target != 2] # убедимся, что в целевой переменной осталось только два класса np.unique(wine.target) |
Найдем корреляцию между целевой переменной и содержанием пролина (proline).
|
# оставим только интересующие нас столбцы wine = wine[[‘proline’, ‘target’]] wine.head(3) |
Теперь напишем функцию для расчета точечно-бисериальной корреляции (будем использовать формулу для выборки).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
# объявим функцию для расчета точечно-бисериальной корреляции # функция будет принимать два параметра: количественную и качественную переменные def pbc(continuous, binary): # преобразуем количественную переменную в массив Numpy continuous_values = np.array(continuous) # классы качественной переменной превратим в нули и единицы binary_values = np.unique(binary, return_inverse = True)[1] # создадим две подгруппы количественных наблюдений # в зависимости от класса дихотомической переменной group0 = continuous_values[np.argwhere(binary_values == 0).flatten()] group1 = continuous_values[np.argwhere(binary_values == 1).flatten()] # найдем средние групп, mean0, mean1 = np.mean(group0), np.mean(group1) # а также длины групп и всего датасета n0, n1, n = len(group0), len(group1), len(continuous_values) # рассчитаем СКО количественной переменной std = continuous_values.std() # подставим значения в формулу return (mean1 — mean0) / std * np.sqrt( (n1 * n0) / (n * (n—1)) ) |
Применим эту функцию для нахождения корреляции между пролином и классом вина.
|
pbc(wine[‘proline’], wine[‘target’]) |
Для расчета корреляции мы также можем воспользоваться функцией из библиотеки Scipy.
|
# импортируем модуль stats из библиотеки scipy from scipy import stats # передадим данные в функцию и выведем первый результат[0] stats.pointbiserialr(wine[‘proline’], wine[‘target’])[0] |
Небольшие различия связаны с тем, что функция библиотеки Scipy использует формулу для генеральной совокупности.
Что интересно, математически коэффициент точечно-бисериальной корреляции дает тот же результат, что и коэффициент корреляции Пирсона.
|
# сравним в корреляцией Пирсона wine.corr().iloc[0,1] |
Пояснения к коду
Сделаем пояснения к приведенному коду. Упростим пример и предположим, что нам нужно рассчитать, есть ли зависимость между количеством сна и результатом экзамена.
|
# количество сна в часах поместим в массив Numpy sleep = np.array([6, 8, 9, 7]) # результат будет записан с помощью двух категорий pass и fail exam = [‘pass’, ‘fail’, ‘pass’, ‘fail’] |
Для расчета точечно-бисериальной корреляции нам нужно разделить данные о сне в зависимости от результата экзамена на две группы. В первую очередь, преобразуем строковые значения переменной exam в числа. Для этого, в частности, мы можем использовать функцию np.unique() с параметром return_inverse = True.
|
exam_encoded = np.unique(exam, return_inverse = True) exam_encoded |
|
(array([‘fail’, ‘pass’], dtype='<U4′), array([1, 0, 1, 0])) |
Вторым результатом [1] будут числовые значения категорий. Теперь используем функцию np.argwhere(), чтобы найти индексы тех, кто сдал экзамены и тех, кто не сдал.
|
# функция выводит индексы элементов, соответствующих заданному условию fail_index = np.argwhere(exam_encoded[1] == 0) pass_index = np.argwhere(exam_encoded[1] == 1) |
|
# студенты, провалившие тест, должны быть на втором и четвертом местах fail_index |
|
# сдавшие — на первом и третьем pass_index |
Остается убрать второе измерение массивов.
|
fail_index, pass_index = fail_index.flatten(), pass_index.flatten() |
|
(array([1, 3]), array([0, 2])) |
Теперь используем индексы для группировки часов сна в зависимости от результатов экзамена.
|
sleep[fail_index], sleep[pass_index] |
|
(array([8, 7]), array([6, 9])) |
Теперь мы можем легко посчитать нужные метрики и подставить их в формулу точечно-бисериальной корреляции.
Корреляционное отношение
Корреляционное отношение (correlation ratio) выявляет взаимосвязь между количественной переменной и категориальной переменной с любым количеством категорий. Смысл этой метрики лучше всего понять на простом примере из Википедии⧉.
Простой пример
Предположим, что у нас есть результаты экзаменов по трем предметам (алгебре, геометрии и статистике), и нам нужно понять, есть ли взаимосвязь между предметом и поставленными оценками. Взглянем на данные:
- алгебра: 45, 70, 29, 15, 21 (5 оценок)
- геометрия: 40, 20, 30, 42 (4 оценки)
- статистика: 65, 95, 80, 70, 85, 73 (6 оценок)
Шаг 1. Найдем средние значения внутри каждой группы и общее среднее всех наблюдений.
- алгебра: 36
- геометрия: 33
- статистика: 78
- общее среднее: 52
Шаг 2. Теперь найдем, насколько наблюдения в каждой из групп отличаются от группового среднего. Возведем результаты в квадрат для того, чтобы положительные и отрицательные значения не взаимоудалялись, и сложим их. Например, для алгебры сумма квадратов отклонений от среднего будет равна
$$ (36-45)^2+(36-70)^2+(36-29)^2+(36-15)^2+(36-21)^2 = 1959 $$
Для геометрии — 308, для статистики — 600. Сложим внутригрупповые отклонения от среднего и получим $1959+308+600=2860$
Сумма квадратов отклонений всех наблюдений от общего среднего составит 9640.
Шаг 3. Теперь выясним, какую долю в общей дисперсии составляет внутригрупповая дисперсия. Для этого разделим 2860 на 9640.
$$ frac{2860}{9640} approx 0,29668 $$
Соответственно доля не объясненных внутригрупповой дисперсией отклонений (ее принято обозначать греческой буквой $eta$, «эта») составляет
$$ eta^2 = 1-frac{2860}{9640} approx 0,70332 $$
Логично предположить, что чем выше доля не объясненных внутригрупповыми отклонениями дисперсии (чем выше $eta^2$), тем большую важность имеет дисперсия между группами. Другими словами, тем важнее отклонения между предметами, а не между оценками внутри каждого предмета.
Значит, чем выше $eta^2$, тем теснее связь между категориями и количественными оценками.
Шаг 4. Извлечем корень из получившегося значения для того, чтобы вернуться к исходным единицам измерения.
$$ eta = sqrt{0,70332} approx 0,83864 $$
Подведем итог. Корреляционное отношение изменяется от 0 до 1. Если показатель равен нулю, общая дисперсия объясняется исключительно внутригрупповыми отклонениями и связи между качественной и количественной переменными нет. Если показатель равен единице, общая дисперсия полностью объясняется только дисперсией между группами и связь между переменными велика.
Можно также сказать, что если $eta$ равна нулю, то внутригрупповые средние одинаковы, если $eta$ равна единице, все значения в каждой из категорий должны быть одинаковы (например, все студенты по алгебре должны получить одинаковую оценку и т.д.).
Еще один способ расчета
Для расчета корреляционного отношения можно также найти взвешенные по количеству элементов квадраты отклонений общего среднего от внутригрупповых средних. Для примера выше арифметика выглядит следующим образом
$$ 5(36-52)^2+4(33-52)^2+6(78-52)^2 = 6780 $$
Обратите внимание, это то же самое, что и $9640-2860=6780$, то есть сумма отклонений, не объясняемых внутригрупповой дисперсией. Таким образом,
$$ eta^2 = frac{6780}{9640} approx 0,70332 $$
$$ eta = sqrt{0,70332} approx 0,83864 $$
Остается написать функцию для расчета корреляционного отношения на Питоне.
Код на Питоне
Используем те же данные, что и в примере выше.
|
# создадим датафрейм с результатами экзаменов по трем предметам test = pd.DataFrame({ # используем список с названиями предметов ‘subject’ : [‘algebra’] * 5 + [‘geometry’] * 4 + [‘stats’] * 6, # и соответствующими оценками ‘score’ : [45, 70, 29, 15, 21, 40, 20, 30, 42, 65, 95, 80, 70, 85, 73 ] }) |
Вначале возьмем значения оценок, рассчитаем сумму квадратов отклонений от среднего значения, а также закодируем категориальные переменные числами. Для этого как и ранее в случае точечно-бисериальной корреляцией используем функцию np.unique() с параметров return_inverse = True.
|
# возьмем значения оценок values = np.array(test.score) # и рассчитаем сумму квадратов отклонений от среднего значения ss_total = np.sum((values.mean() — values) ** 2) # закодируем категории предметов числами cats = np.unique(test.subject, return_inverse = True)[1] cats |
|
array([0, 0, 0, 0, 0, 1, 1, 1, 1, 2, 2, 2, 2, 2, 2]) |
Теперь применим первый вариант расчета корреляционного отношения.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
# объявим переменную для внутригрупповой дисперсии ss_ingroups = 0 # в цикле, состоящем из количества категорий for c in np.unique(cats): # вычленим группу оценок по каждому предмету group = values[np.argwhere(cats == c).flatten()] # найдем суммы квадратов отклонений значений от групповых средних # и сложим эти результаты для каждой группы ss_ingroups += np.sum((group.mean() — group) ** 2) # найдем долю внутригрупповой дисперсии и вычтем ее из единицы eta_squared = 1 — ss_ingroups/ss_total # найдем корень из предыщущего значения eta = np.sqrt(eta_squared) # это и будет корреляционное отношение eta |
Напомню, что использование функции np.argwhere() мы уже рассмотрели ранее на этом занятии. Рассчитаем по второму варианту.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# объявим переменную для межгрупповой дисперсии ss_betweengroups = 0 # в цикле, состоящем из количества категорий, for c in np.unique(cats): # вычленим группу оценок по каждому предмету group = values[np.argwhere(cats == c).flatten()] # для каждой группы # найдем взвешенный по количеству элементов в группе # квадрат отклонения группового среднего от общего среднего # и сложим результаты ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 # найдем долю межгрупповой дисперсии eta_squared = ss_betweengroups/ss_total # найдем корень из предыщущего значения eta = np.sqrt(eta_squared) # это и будет корреляционное отношение eta |
Мы готовы написать функции.
|
# вариант 1 def correlation_ratio1(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_ingroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_ingroups += np.sum((group.mean() — group) ** 2) return np.sqrt(1 — ss_ingroups/ss_total) |
|
# проверим результат correlation_ratio1(test.score, test.subject) |
|
# вариант 2 def correlation_ratio2(numerical, categorical): values = np.array(numerical) ss_total = np.sum((values.mean() — values) ** 2) cats = np.unique(categorical, return_inverse = True)[1] ss_betweengroups = 0 for c in np.unique(cats): group = values[np.argwhere(cats == c).flatten()] ss_betweengroups += len(group) * (group.mean() — values.mean()) ** 2 return np.sqrt(ss_betweengroups/ss_total) |
|
# проверим результат correlation_ratio2(test.score, test.subject) |
Подведем итог
Для удобства, давайте обобщим, какие методы и когда можно использовать.
- Если речь идет о двух количественных переменных мы можем использовать:
- коэффициент Пирсона, если речь идет о выявлении линейной зависимости
- коэффициенты Спирмена и Кендалла, если требуется оценить нелинейную взаимосвязь
- В случае двух категориальных переменных, подойдут:
- уже упомянутые коэффициенты Спирмена и Кендалла для порядковых категорий, а также
- коэффициент неопределенности Тиля
- Когда перед нами одна количественная и одна категориальная переменные, мы можем рассчитать:
- точечно-бисериальный коэффициент корреляции, в случае, если категориальная переменная имеет дихотомическую шкалу; или
- корреляционное отношение в случае множества категорий
Вопросы для закрепления
Вопрос. Чем параметрические тесты отличаются от непараметрических?
Посмотреть правильный ответ
Ответ: параметрический тест показывает корректный результат, если данные, на которых он основывается соответствуют определенным критериям или допущениям, для непараметрического теста такие критерии отсутствуют.
При этом обратите внимание, отсутствие допущений не отменяет ограничения на применение тестов только к определенным типам данных. Например, метод Спирмена, как уже было сказано, не подойдет для выявления немонотонной зависимости.
Вопрос. При расчете коэффициента корреляции Пирсона, что дает деление ковариации на произведение СКО двух переменных $s_x s_y$?
Посмотреть правильный ответ
Ответ: таким образом мы выражаем любую ковариацию как долю от произведения двух СКО и, как следствие, можем измерять силу взаимосвязи двух переменных и сравнивать коэффициенты корреляции между собой.
Вопрос. Что такое симметричность и несимметричность корреляционного метода?
Посмотреть правильный ответ
Ответ: симметричный метод покажет одинаковую силу взаимосвязи переменной X с переменной Y, и переменной Y с переменной X даже если в действительности взаимосвязь не одинаковая; несимметричный метод покажет разную корреляцию X с Y и Y с X, если такое различие действительно существует.
Полезные ссылки
- Библиотека dython⧉. Прямые ссылки на документацию⧉ и исходный код⧉ функций.
Корреляция показывает степень совместного изменения двух признаков. При этом, как уже было сказано, в корреляционном анализе нет зависимых и независимых переменных. Они эквивалентны.
Количественным предсказанием одной переменной (зависимой) на основании другой (независимой) занимается регрессионный анализ.