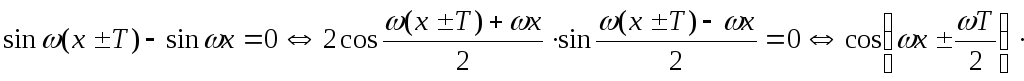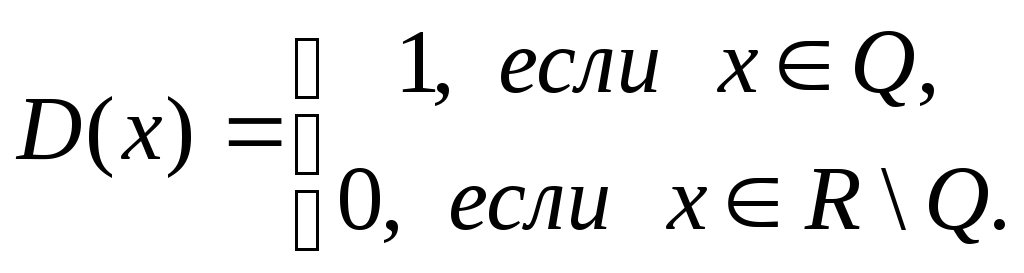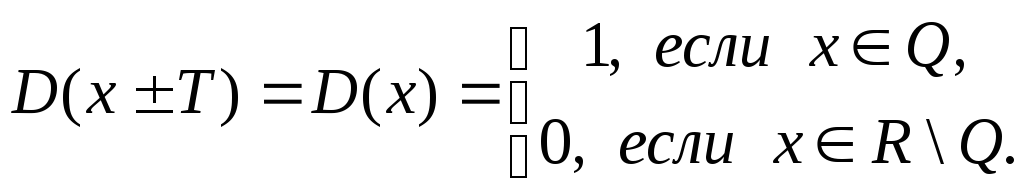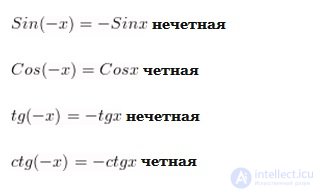Способы задания функции
Пусть функция задается формулой: y=2x^{2}-3. Назначая любые значения независимой переменной x, можно вычислить, пользуясь данной формулой соответствующие значения зависимой переменной y. Например, если x=-0,5, то, пользуясь формулой, получаем, что соответствующее значение y равно y=2 cdot (-0,5)^{2}-3=-2,5.
Взяв любое значение, принимаемое аргументом x в формуле y=2x^{2}-3, можно вычислить только одно значение функции, которое ему соответствует. Функцию можно представить в виде таблицы:
| x | −2 | −1 | 0 | 1 | 2 | 3 |
| y | −4 | −3 | −2 | −1 | 0 | 1 |
Пользуясь данной таблицей, можно разобрать, что для значения аргумента −1 будет соответствовать значение функции −3; а значению x=2 будет соответствовать y=0 и т.д. Также важно знать, что каждому значению аргумента в таблице соответствует лишь одно значение функции.
Еще функции возможно задать, используя графики. С помощью графика устанавливается какое значение функции соотносится с определенным значением x. Наиболее часто, это будет приближенное значение функции.
Четная и нечетная функция
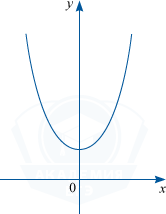
Функция является четной функцией, когда f(-x)=f(x) для любого x из области определения. Такая функция будет симметрична относительно оси Oy.
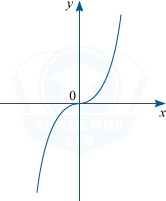
Функция является нечетной функцией, когда f(-x)=-f(x) для любого x из области определения. Такая функция будет симметрична относительно начала координат O (0;0).
Функция является ни четной, ни нечетной и называется функцией общего вида, когда она не обладает симметрией относительно оси или начала координат.
Исследуем на четность нижеприведенную функцию:
f(x)=3x^{3}-7x^{7}
D(f)=(-infty ; +infty ) с симметричной областью определения относительно начала координат. f(-x)= 3 cdot (-x)^{3}-7 cdot (-x)^{7}= -3x^{3}+7x^{7}= -(3x^{3}-7x^{7})= -f(x).
Значит, функция f(x)=3x^{3}-7x^{7} является нечетной.
Периодическая функция
Функция y=f(x), в области определения которой для любого x выполняется равенство f(x+T)=f(x-T)=f(x), называется периодической функцией с периодом T neq 0.
Повторение графика функции на любом отрезке оси абсцисс, который имеет длину T.
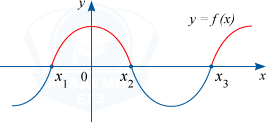
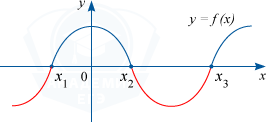
Промежутки, где функция положительная, то есть f(x) > 0 — отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих выше оси абсцисс.
f(x) > 0 на (x_{1}; x_{2}) cup (x_{3}; +infty )
Промежутки, где функция отрицательная, то есть f(x) < 0 — отрезки оси абсцисс, которые отвечают точкам графика функции, лежащих ниже оси абсцисс.
f(x) < 0 на (-infty; x_{1} ) cup (x_{2}; x_{3} )
Ограниченность функции
Ограниченной снизу принято называть функцию y=f(x), x in X тогда, когда существует такое число A, для которого выполняется неравенство f(x) geq A для любого x in X.
Пример ограниченной снизу функции: y=sqrt{1+x^{2}} так как y=sqrt{1+x^{2}} geq 1 для любого x.
Ограниченной сверху называется функция y=f(x), x in X тогда, когда существует такое число B, для которого выполняется неравенство f(x) neq B для любого x in X.
Пример ограниченной снизу функции: y=sqrt{1-x^{2}}, x in [-1;1] так как y=sqrt{1+x^{2}} neq 1 для любого x in [-1;1].
Ограниченной принято называть функцию y=f(x), x in X тогда, когда существует такое число K > 0, для которого выполняется неравенство left | f(x) right | neq K для любого x in X.
Пример ограниченной функции: y=sin x ограничена на всей числовой оси, так как left | sin x right | neq 1.
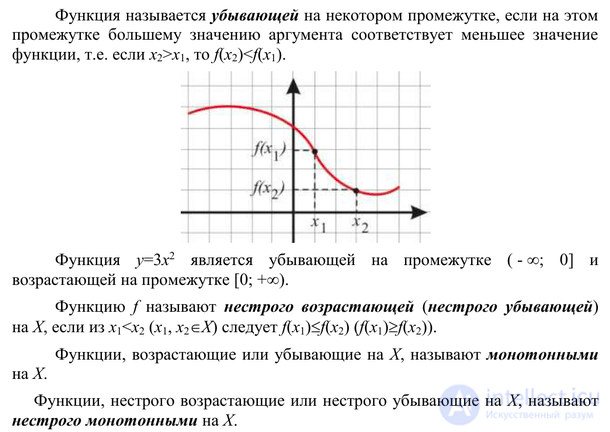
Возрастающая и убывающая функция
О функции, что возрастает на рассматриваемом промежутке принято говорить как о возрастающей функции тогда, когда большему значению x будет соответствовать большее значение функции y=f(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значения аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) > y(x_{2}).
Функция, что убывает на рассматриваемом промежутке, называется убывающей функцией тогда, когда большему значению x будет соответствовать меньшее значение функции y(x). Отсюда выходит, что взяв из рассматриваемого промежутка два произвольных значений аргумента x_{1} и x_{2}, причем x_{1} > x_{2}, будет y(x_{1}) < y(x_{2}).
Корнями функции принято называть точки, в которых функция F=y(x) пересекает ось абсцисс (они получаются в результате решения уравнения y(x)=0).
а) Если при x > 0 четная функция возрастает, то убывает она при x < 0
б) Когда при x > 0 четная функция убывает, то возрастает она при x < 0
в) Когда при x > 0 нечетная функция возрастает, то возрастает она и при x < 0
г) Когда нечетная функция будет убывать при x > 0, то она будет убывать и при x < 0
Экстремумы функции
Точкой минимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняться неравенство f(x) > f(x_{0}). y_{min} — обозначение функции в точке min.
Точкой максимума функции y=f(x) принято называть такую точку x=x_{0}, у которой ее окрестность будет иметь остальные точки (кроме самой точки x=x_{0}), и для них тогда будет выполняется неравенство f(x) < f(x^{0}). y_{max} — обозначение функции в точке max.
Необходимое условие
Согласно теореме Ферма: f'(x)=0 тогда, когда у функции f(x), что дифференцируема в точке x_{0}, появится экстремум в этой точке.
Достаточное условие
- Когда у производной знак меняется с плюса на минус, то x_{0} будет точкой минимума;
- x_{0} — будет точкой максимума только тогда, когда у производной меняется знак с минуса на плюс при переходе через стационарную точку x_{0}.
Наибольшее и наименьшее значение функции на промежутке
Шаги вычислений:
- Ищется производная f'(x);
- Находятся стационарные и критические точки функции и выбирают принадлежащие отрезку [a; b];
- Находятся значения функции f(x) в стационарных и критических точках и концах отрезка. Меньшее из полученных результатов будет являться наименьшим значением функции, а большее — наибольшим.
Определение 1. Функцияназываетсячетной (нечетной),
если вместе с каждым значением переменнойзначение –хтакже принадлежит
и выполняется равенство
(11.1)
Таким образом, функция может быть четной
или нечетной только тогда, когда ее
область определения симметрична
относительно начала координат на
числовой прямой (числа х и –ходновременно принадлежат).
Например, функцияне является четной и нечетной, так как
ее область определенияне симметрична относительно начала
координат.
Функция
четная, так как
симметрична относительно начала
координат и.
Функция
нечетная, так как
и
.
Функция
не является четной и нечетной, так как
хотяи симметрична относительно начала
координат, равенства (11.1) не
выполняются. Например,.
График четной функции симметричен
относительно оси Оу, так как если
точкапринадлежит графику, то и точка
тоже принадлежит графику. График нечетной
функции симметричен относительно начала
координат, так как еслипринадлежит графику, то и точка
тоже принадлежит графику.
При доказательстве четности или
нечетности функции бывают полезны
следующие утверждения.
Теорема 1. а) Сумма двух четных
(нечетных) функций есть функция четная
(нечетная).
б) Произведение двух четных (нечетных)
функций есть функция четная.
в) Произведение четной и нечетной функций
есть функция нечетная.
г) Если f– четная
функция на множествеХ, а функцияg определена на
множестве,
то функция–
четная.
д) Если f– нечетная
функция на множествеХ, а функцияg определена на
множествеи четная (нечетная), то функция
–
четная (нечетная).
Доказательство. Докажем, например,
б) и г).
б) Пусть
и
–
четные функции. Тогда,
поэтому.
Аналогично рассматривается случай
нечетных функцийи
.
г) Пусть f – четная
функция. Тогда.
Остальные утверждения теоремы доказываются
аналогично. Теорема доказана.
Теорема 2. Любую функцию,
заданную на множествеХ, симметричном
относительно начала координат, можно
представить в виде суммы четной и
нечетной функций.
Доказательство. Функциюможно записать в виде
.
Функция
– четная, так как
,
а функция– нечетная, поскольку
.
Таким образом,,
где–
четная, а–
нечетная функции. Теорема доказана.
Определение 2. Функцияназываетсяпериодической, если
существует число,
такое, что при любомчисла
и
также
принадлежат области определенияи выполняются равенства
.
Такое число Tназываетсяпериодом функции.
Из определения 1 следует, что если Т
– период функции,
то и число –Т тоже является
периодом функции (так
как при заменеТ на –Т равенство
сохраняется). С помощью метода
математической индукции можно показать,
что еслиТ– период функцииf,
то и,
тоже является периодом. Отсюда следует,
что если функция имеет период, то она
имеет бесконечно много периодов.
Определение 3. Наименьший из
положительных периодов функции называется
ееосновным периодом.
Теорема 3. ЕслиТ– основной
период функцииf, то
остальные периоды кратны ему.
Доказательство. Предположим
противное, то есть что существует периодфункцииf (
>0),
не кратныйТ. Тогда, разделивнаТ с остатком, получим
,
где.
Поэтому
,
то есть
– период функцииf,
причем,
а это противоречит тому, чтоТ–
основной период функцииf.
Из полученного противоречия следует
утверждение теоремы. Теорема доказана.
Хорошо известно, что тригонометрические
функции являются периодическими.
Основной период
и
равен
,
и
.
Найдем период функции.
Пусть— период этой функции. Тогда
(так как
.
Отсюда
или
или
или
.
Значение T, определяемое
из первого равенства, не может быть
периодом, так как зависит отх, т.е.
является функцией отх, а не постоянным
числом. Период определяется из второго
равенства:.
Периодов бесконечно много, принаименьший
положительный период получается при:
.
Это – основной период функции.
Примером более сложной периодической
функции является функция Дирихле
Заметим, что если T–
рациональное число, тои
являются рациональными числами при
рациональномхи иррациональными
при иррациональномх. Поэтому
при любом рациональном числе T.
Следовательно, любое рациональное числоTявляется периодом
функции Дирихле. Ясно, что основного
периода у этой функции нет, так как есть
положительные рациональные числа, сколь
угодно близкие к нулю (например,
рациональное числоможно сделать выборомnсколь угодно близким к нулю).
Теорема 4. Если функцияf
задана на множествеХи имеет
периодТ, а функцияg
задана на множестве,
то сложная функциятоже имеет периодТ.
Доказательство. Имеем,
поэтому
,
то есть утверждение теоремы доказано.
Например, так как cos
x имеет период,
то и функцииимеют период
.
Определение 4. Функции, не являющиеся
периодическими, называютсянепериодическими.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Алгебра и начала математического анализа, 11 класс
Урок №2 Чётность и нечётность тригонометрических функций. Периодичность.
Перечень вопросов, рассматриваемых в теме
- Изучение чётности функции,
- Построение периодичности функции,
- Определение четности или нечетности тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|,
- Объяснение зависимости четности или нечетность функции вида y=af(kx+b)+c и y=|f(k|x|+b)|,
- Определение периодичности тригонометрических функций вида y=af(kx+b)+c и y=|f(k|x|+b)|,
- Объяснение зависимости периодичности функции вида y=af(kx+b)+c и y=|f(k|x|+b)|,
Глоссарий по теме
Функцию y=f(x), x∈X называют чётной, если для любого значения xиз множества X выполняется равенство f(−x)=f(x).
Функцию y=f(x), x∈X называют нечётной, если для любого значения x из множества X выполняется равенство f(−x)=−f(x).
Период функций, представляющих собой сумму непрерывных и периодических функций, равен наименьшему кратному периодов слагаемых, если он существует.
Основная литература:
Колягин Ю.М., Ткачева М.В., Федорова Н.Е. и др., под ред. Жижченко А.Б Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2010.–336 с.
Дополнительная литература:
Шахмейстер, А.Х. Тригонометрия / А.Х. Шахмейстер.— СПб.: Петроглиф, 2014. — 750 с.
Открытые электронные ресурсы:
Открытый банк заданий ЕГЭ ФИПИ [Электронный ресурс].– Режим доступа: http://ege.fipi.ru/
Решу ЕГЭ образовательный портал для подготовки к экзаменам [Электронный ресурс].– Режим доступа: https://ege.sdamgia.ru/
Теоретический материал для самостоятельного изучения
Косинус (cos α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины прилежащего катета |ОА| к длине гипотенузы |ОВ|.
Область. определения функции (D) — множество R всех действительных чисел
Множество значений функции (E) — отрезок [-1; 1], т.е. косинус функция —ограниченная.
Для того, чтобы определить чётность функции косинус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, cos(60°) = ½ = cos(–60°)–это значит, что : cos(−x)=cos x для всех x∈R и у=сosx–чётная
Сиинус(sin α) – это тригонометрическая функция от угла α между гипотенузой и катетом прямоугольного треугольника, равная отношению длины противолежащего катета |АВ| к длине гипотенузы |ОВ|.
Область определения функции (D) — множество R всех действительных чисел.
Множество значений функции (E) — отрезок [-1; 1], т.е. синус функция —ограниченная.
Для того, чтобы определить чётность функции синус проверим следующие определения: функция чётная, f(−x)=f(x) и функцию нечётная, f(−x)=−f(x).
Например, sin(30°) = ½ sin(–30°) = –½ –это значит, что : sin(−x)=–sin (x) для всех x∈R и y=sinx–нечётная


Период функций y=sin x, y=cos xравен 2π, период функций tgx, ctgx равен π.
Примеры и разборы решения заданий тренировочного модуля
Пример 1. Выясним, является ли функция
чётной или нечётной?
Пример 2. Доказать, что число 2π является наименьшим положительным периодом функции y=cos x
Пусть Т>0 – период косинуса, т.е. для любого х выполняется равенство cos (x+T)= cos x. Положив х=0, получим cos T=1. Отсюда Т=2πk, x∈R. Так как Т>0, то может принимать значения 2π, 4π, 6π,…, и поэтому период не может быть меньше 2π
Описание презентации по отдельным слайдам:
-
1 слайд
Периодичность, четность и нечетность функций
-
2 слайд
ПЛАН
I. Изучение нового материала1) Частично-поисковый (эвристический) метод:
а) проблема построения графика четной, нечетной, периодической
функции на всей её области определения;
б) формирование гипотез;
в) обсуждение.
P.S. Можно в групповой форме2) Определение четной, нечетной, периодической функций.
P.S. Деятельностный подход: дети составляют схему определения
понятий четной, нечетной, периодической функции.3) Схема исследования функции на четность, нечетность, периодичность:
а) составление схемы исследования;
б) составление алгоритма (можно по частично заполненному).4) Свойства четной, нечетной, периодической функций:
а) построение графиков простейших функций;
б) периодичность функции y=Af(kx+b) (с доказательством для 3-го уровня).
P.S. Дети составляют таблицу свойств функции с графической интерпретацией.5) Закрепление опыта переработки информации:
а) дети сами приводят примеры для п. 3) и 4);
б) вопросы, проблемы, обсуждение, рецензии. -
3 слайд
II. Семинар-практикум с компьютерной поддержкой
1) Фронтальная работа на 1 уровне:
а) составить соседу по одному примеру на исследование функции на четность,
нечетность, периодичность;
б) построение графика по его части (на доске);
в) обсуждение результатов.2) Срезовая работа (тест):
а) определения;
б) исследование функций;
в) свойства графиков.
P.S. По итогам работы формируются группы.3) Групповая работа (решение задач):
а) за ПК с обучающей программой – 1 уровень;
б) в группах и с учителем – 2,3 уровень;
в) консультанты для ПК из 2,3 уровня;
г) отчет групп, обсуждение, рецензии;
д) подведение итогов.
P.S. Саморегуляция и при решении задач, и при выборе уровня и группы.III. Контроль и коррекция
1) Собственные образовательные продукты: программа для ПК; презентация;
творческий отчет; исследовательская работа на углубленном уровне.
2) Контрольная трехуровневая работа или зачет, составленные детьми.
3) Коррекция и закрепление опыта эмоционально-ценностного отношения.
P.S. Для разработчиков компьютерной программы зачет автоматом. -
4 слайд
ЦЕЛИ
Урок 1. Изучение нового материала.Цель I. Приобретение и преобразование учебной информации и становление умений.
Уровень 1. Составляет схему определения четной, нечетной, периодической функции с использованием подсказок; сравнивает исследования однотипных функций 1-го уровня.
Уровень 2. Сам или с использованием набора объектов взаимосвязи составляет схему определения понятий; обобщает исследования и построение графиков однотипных функций.
Уровень 3. Сам составляет схему определения понятий; составляет приемы исследования и построения графиков функций сам или по плану. -
5 слайд
ЦЕЛИ
Уроки 2, 3 (пара). Семинар-практикум с компьютерной поддержкой.Цель II. Контроль усвоения теории.
Знает: определения четной, нечетной, периодической функций; схему исследования функции; свойства графиков и способ их построения.
Цель III. Применение знаний и умений при решении задач.
Уровень 1. Исследует простейшие функции; достраивает график по его части и свойству функции.
Уровень 2. Использует преобразования для исследования функции; строит график функции (задачи 2-го уровня).
Уровень 3. Исследует функцию, преобразуя формулу; исследует сумму, разность функций; строит графики(задачи 3-го уровня); составляет задачи 1,2-го уровня.Цель IV. Формирование коммуникативных умений.
Работает в группе; рецензирует ответы предыдущих уровней; оказывает взаимопомощь.Цель V. Формирование организационных умений.
Ставит цели; выбирает задачи; проводит самопроверку. -
6 слайд
ЦЕЛИ
Урок 4. Контроль и коррекция.Цель V. Формирование организационных умений.
Составляет контрольную работу своего уровня; оценивает свою работу; планирует коррекцию УПД.
Урок 5. Резерв.P.S. Предложенная структура изучения довольно сложна и непредсказуема в деталях, т.к. зависит от большого количества факторов. Поэтому, предусмотрен резервный урок.
-
7 слайд
СРЕДСТВА
1) Обучающая программа для ПК 1-го уровня ,разработанная учителем или учениками под руководством учителя, или лицензионная.2) Алгоритмы (пустые или частично заполненные) для исследования функции на четность, нечетность, периодичность.
3) Готовые чертежи графиков, заданных на части области определения функции.
4) Таблицы свойств функции с графической интерпретацией.
5) Тесты для срезовой работы с быстрой проверкой.
6) Карточки с заданиями для групповой работы.
7) Мультимедийные средства для разработки и демонстрации детьми собственных образовательных продуктов.
-
8 слайд
ОБУЧАЮЩАЯ ПРОГРАММА
К сожалению, по этой теме составить образец обучающей программы на данный момент не представляется возможным по техническим причинам.Приведем пример разработанных ранее учителем и учениками обучающих программ по другим темам.
Примите извинения за доставленные неудобства.
Спасибо.
Привет, сегодня поговорим про функции, обещаю рассказать все что знаю. Для того чтобы лучше понимать что такое
функции, область определения, область значения, четность функции, нечетность функции, периодичность функции, возрастание функции, убывание функции, преобразования графиков функций , настоятельно рекомендую прочитать все из категории СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА.
функции
Числовой функцией с областью определения D называется соответствие, при котором каждому числу x из множества D сопоставляется по некоторому правилу единственное число y, зависящее от x.
Обозначение: y = f(x)
Независимая переменная x – аргумент функции f.
Число y, соответствующее x – значение функции f в точке x.
График функции
График функции f – множество всех точек (x; y) координатной плоскости, где y=f(x), а x «пробегает» всю
область определения функции f.
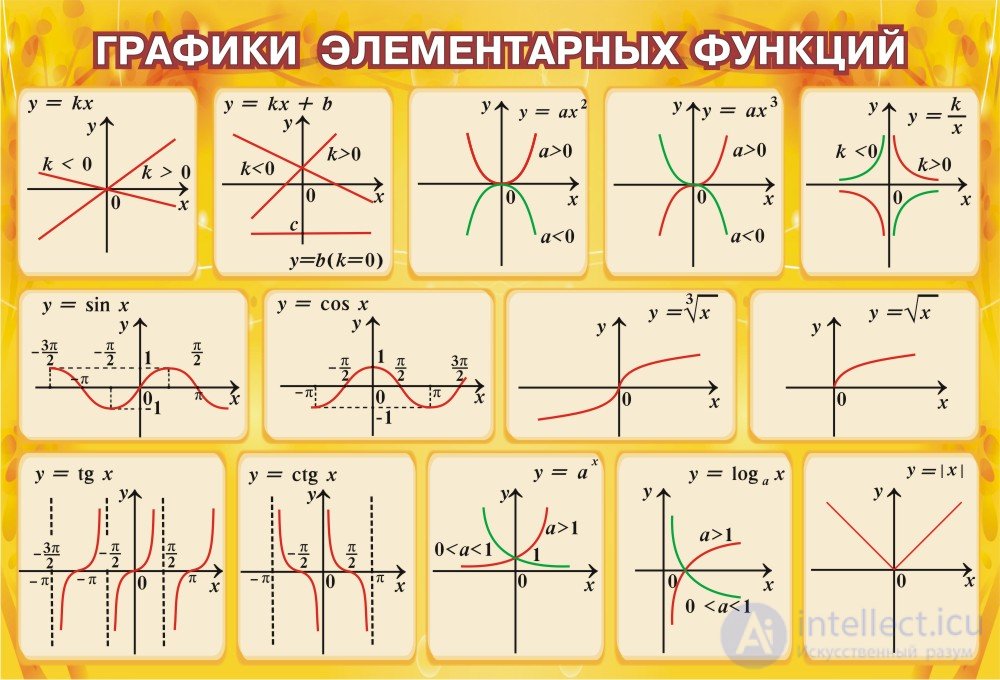
Графики элементарных функций
Область определения функции ООФ
Область определения функции – множество значений x, для которых выполнимы действия, указанные в правиле f.
Обозначается: ООФ или D(f).
С геометрической точки зрения ООФ есть проекция графика этой функции на ось ОХ.
область значения функции ОЗФ
Область значений функции – множество значений функции f(x), которые она принимает при изменении x на ООФ.
Обозначается: ОЗФ или E(f).
С геометрической точки зрения ОЗФ – проекция графика на ось OY.
Четность и нечетность функций
Функция f называется четной, если для любых x из ООФ
f(-x) = f(x)
График четной функции симметричен относительно оси OY.
Функция f называется нечетной, если для любых x из ООФ f(-x) = — f(x)
График нечетной функции симметричен относительно начала координат.
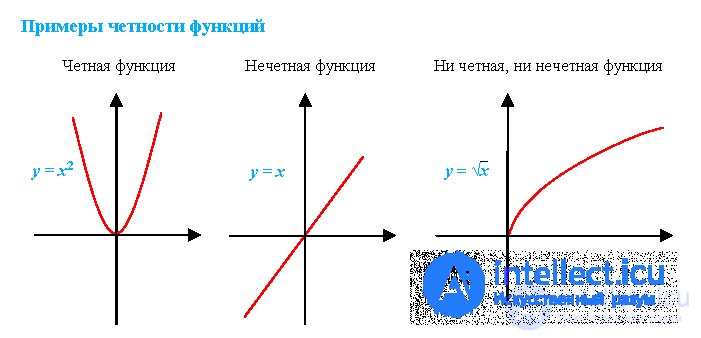
Алгоритм определения четности функции одной переменной

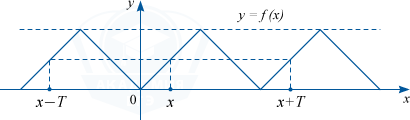
Периодичность функций
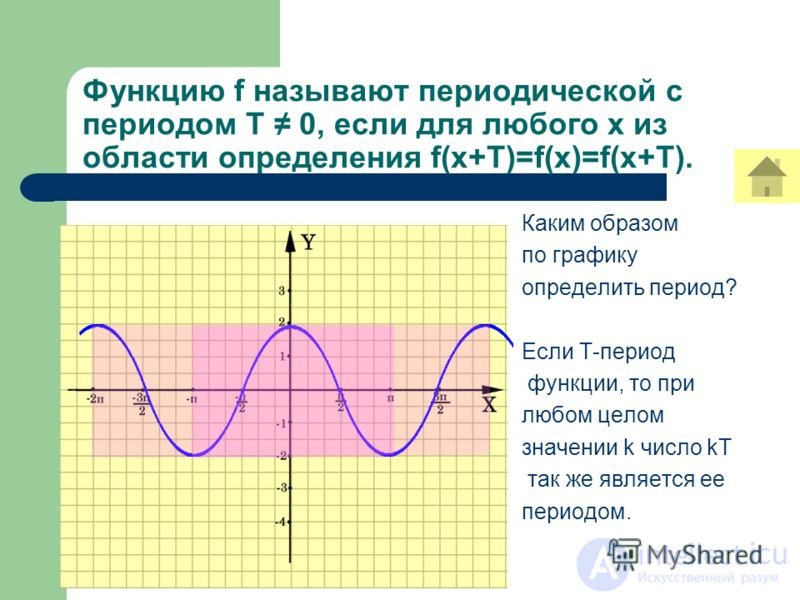
Функция называется периодической с периодом Т ≠ 0, если для любого x из ООФ
f(x + T) = f(x) = f(x — T).
Для построения графика периодичностью функции с периодом T достаточно провести построение на отрезке длиной T и полученный график параллельно перенести на расстояние nT вправо и влево вдоль оси OX (n – любое натуральное число).
Возрастание, убывание функций
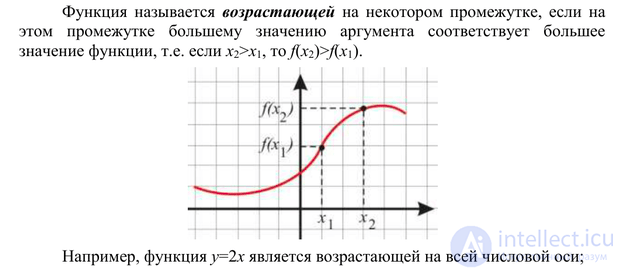
Функция f возрастает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1, выполнено неравенство f(x2) > f(x1).
Функция f убывает на множестве P, если для любых x1 и x2 из множества P, таких, что x2 > x1, выполнено неравенство f(x2) < f(x1).
преобразования графиков функций
Пусть дан график функции y = f(x)
Тогда:
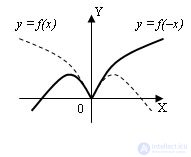
1 . Об этом говорит сайт https://intellect.icu . График функции y = f(–x) получается симметричным отображением графика y = f(x) относительно оси OY:
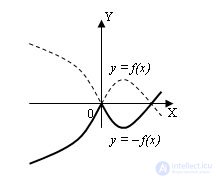
2 . График функции y = –f(x) получается симметричным отображением графика y = f(x) относительно оси OX:
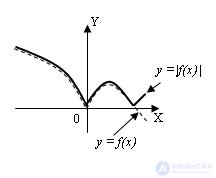
3 . График функции y = |f(x)| получается следующим образом: обводим ту часть графика функции y = f(x), которая лежит выше оси OX, а часть лежащую ниже отобразить симметрично оси OX:
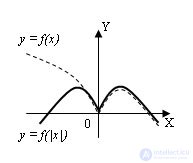
4 . График функции y =f(|x|) получается следующим образом: отбрасываем часть графика функции y = f(x), лежащую левее оси OY, обводим ту часть графика функции y = f(x), которая лежит правее оси OY и отображаем ее симметрично оси OY:
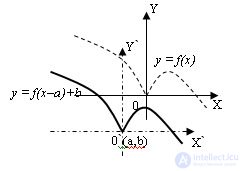
5 .График функции y =f(x–a) + b получается построением графика функции y = f(x) в новой системе координат X`0`Y`, где 0`(a, b), 0`X` || 0X, 0`Y` || 0Y:
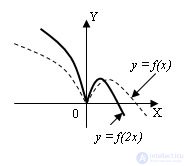
6 . График функции y =f(m*x), m > 0, получается из данного растяжением в 1/m раз (если m < 0) от оси OY (вдоль оси OX) и сжатием в m раз (m > 1) к оси OY:
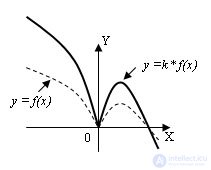
7 . График функции y =k* f(x), k > 0, получается из данного растяжением в k раз (k > 1) относительно оси OX (вдоль оси OY) и сжатием в 1/k раз (при k < 1) к оси OX:
Вау!! 😲 Ты еще не читал? Это зря!
- взаимно обратные функции , обратные функции ,
- обратные тригонометрические функции , арксинус ,
- дзета-функция римана ,
- случайные функции , характеристики случайных функций ,
- каррирование , мемоизация ,
- Функциональное уравнение
- Алгоритм
- Уравнение
- Булева функция
Понравилась статья про функции? Откомментируйте её Надеюсь, что теперь ты понял что такое функции, область определения, область значения, четность функции, нечетность функции, периодичность функции, возрастание функции, убывание функции, преобразования графиков функций
и для чего все это нужно, а если не понял, или есть замечания,
то нестесняся пиши или спрашивай в комментариях, с удовольствием отвечу. Для того чтобы глубже понять настоятельно рекомендую изучить всю информацию из категории
СПРАВОЧНИК ПО МАТЕМАТИКЕ, ШКОЛЬНАЯ МАТЕМАТИКА, ВЫСШАЯ МАТЕМАТИКА
Из статьи мы узнали кратко, но емко про функции

.png)
.png)