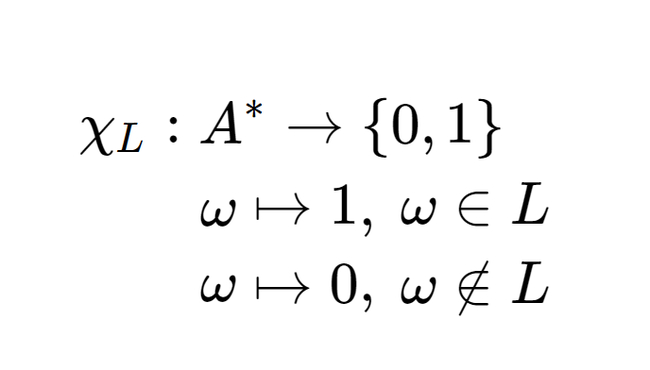Загадка из «Полицейского с Рублевки» остается популярной спустя четыре года
Сценарист и создатель сериала «Полицейский с Рублевки» Илья Куликов ведет свой YouTube-канал, в котором публикует все происходящее за кадром, а также вырезанные из сериала сцены. В одном из таких эпизодов Гриша Измайлов (герой Александра Петрова) просит Яковлева (героя Сергея Бурунова) отгадать дурацкую загадку. Ролик был опубликован в 2017 году, и спустя четыре года эпизод с загадкой все еще приводит зрителей в восторг.
«Есть две машины. Первая машина — седан, радиус колес 18. Вторая машина — пикап, радиус колес 22. Если поменять местами передние колеса с первой машины на задние колеса второй машины, то первая машина поедет, а вторая нет. Почему?» — таковы условия загадки.
Нелепость и одновременная гениальность, а также созданная интрига вокруг этой загадки позволили ролику с отгадкой набрать больше восьми миллионов.
По-факту, загадка и отгадка не имеют прямой связи, однако благодаря актерскому мастерству Сергея Бурунова и Андрея Петрова зрители полюбили этот момент из «Полицейского с Рублевки».
Ответ на загадку очень прост, хотя он никак не связан с условиями задачи: одна из машин лежит на крыше, колесами вверх.
В марте актер Сергей Бурунов отметил свой 44-й день рождения. Его коллега по цеху Александр Петров написал в честь Бурунова четверостишие и опубликовал его в своем Instagram. Как поздравил актер своего друга и товарища, читайте в материале «Слово и Дело».
Стоят 2 машины почему 1 не поедет
Здесь легко и интересно общаться. Присоединяйся!
Вы ж бедную на крышу перевернули.
При одинаковом расстоянии между передним и задним мостом обе машины окажутся с приподнятым носом и опущенным задом, причем угол наклона будет одинаков. только первая машина приподнимет свой нос относительно оси вращения проходящей через задние колеса и вцелом выхлопная труба опустится незначительно так как расположена близко к задним колесам. зато вторая машина опустит свою выхлопную трубу сильнее, так как выхлопная поворачивается (опускается) относительно передних колес, расположенных дальше.
итог — у обеих машин одинаковый наклон (нос вверх а зад вниз) но у второй дополнительно опускание кузова на 4 см в сравнении с первой машиной.
таким образом у второй больше шансов что она будет тереться например выхлопной трубой об землю
Здесь легко и интересно общаться. Присоединяйся!
и почему же посмотрел версии людей сам не пойму вырез крыла
Нееее. напишу все читать будут. Позже
зря. Интерес к вопросу остынет.
а по шпилькам то подойдёт
Вторая машина заднеприводная, первая — с передним приводом
А вот этого я не знаю
Очень интересно.. Вывод делаем, а не знаем.
У нее не будет хватать одной пары колес) потому и не поедет)
Потому что они туда не наденутся.
ну значит пружины подпилены
ну либо у второй машины колеса разных радиусов
тут законы физики- механики работают
Это смотря какие арки колесные, может и поехать, но тяжело
Прочитал))) если задний привод, и задним ходом, победит)
С удовольствием бы. Не видно)
А мне плевать на дураков!
не провернутся большие на меньшем
Не внимательно читаете
представляла и так и так. Пойду на практике попробую
Хорошо. Расскажите потом
Болты не прикрутили
А как же их поставили? Рядышком просто? Нет их прикрутили.
потому что не полезут радиус 16 на 17
что то с дисками тормозными
по- моему у первой машины не будет передних колес
С самого раннего детства мы видим вокруг себя огромное количество механики, техники и других полезных устройств. Вокруг много механизмов: бульдозеры, грузовики, экскаваторы, мотоциклы и автомобили. Эти детские загадки помогут родителям понятно и доходчиво объяснить детям про машины, объяснят принципы работы многих полезных и нужных предметов и явлений. Загадав малышу несколько этих загадок, вы сразу увидите взросление ребенка, его осмысленный взгляд на пролетающие самолеты, проезжающие мимо автомобили или проходящие поезда.
Бывают ли у дождика четыре колеса?
Скажи, как называются такие чудеса?
Ответ: (Поливальная машина )
***
Чудо-дворник перед нами:
Загребущими руками
За одну минуту сгреб
Преогромнейший сугроб.
Ответ: (Снегоуборочная машина )
***
Спешит машина красная,
Не выключая фар,
На службу на опасную,
Спешит тушить пожар!
Ответ: (Пожарная машина )
***
Синяя машина с белой полосой,
Она развозит почту летом и зимой,
Много в ней журналов,
Писем и газет.
И везет она
Тебе пламенный «привет»!
Ответ: (Почтовая машина )
***
Он идёт, волну сечёт,
Из трубы зерно течёт.
Ответ: (Комбайн )
***
Чудо-птица, алый хвост,
Прилетела в стаю звёзд.
Ответ: (Ракета )
***
Запылал у чудища изумрудный глаз.
Значит, можно улицу перейти сейчас.
Ответ: (Светофор )
***
Встало с краю улицы в длинном сапоге
Чучело трёхглазое на одной ноге.
Где машины движутся, где сошлись пути,
Помогает улицу людям перейти.
Ответ: (Светофор )
***
Опоясал каменный ремень
Сотни городов и деревень.
Ответ: (Шоссе )
***
Он с усами, словно жук,
Пассажирам лучший друг.
Коль над ним есть провода,
Отвезёт вас хоть куда.
Ответ: (Троллейбус )
***
Начинает он копать, заменяет сто лопат.
Ответ: (Экскаватор )
***
У песочных ям, у горы крутой
Стоит великан с железной рукой.
Ответ: (Экскаватор )
***
К нам во двор забрался крот,
Роет землю у ворот.
Тонна в рот земли войдёт,
Если крот откроет рот.
Ответ: (Экскаватор )
***
Я в любое время года
И в любую непогоду
Очень быстро в час любой
Провезу вас под землёй.
Ответ: (Метро )
***
Многолюден, шумен, молод,
Под землей грохочет город.
А дома с народом тут
Вдоль по улице бегут.
Ответ: (Метро )
***
Что за машина:
Шея, как у гуся,
сила, как у слона?
Ответ: (Подъёмный кран )
***
Поднимает великан
Груды груза к облакам.
Там, где встанет он, потом
Вырастает новый дом.
Ответ: (Подъёмный кран )
***
Он по рельсам быстро мчал —
Шпалы все пересчитал.
Ответ: (Поезд )
***
В поле лестница лежит,
Дом по лестнице бежит.
Ответ: (Поезд )
***
Полотно, а не дорожка,
Конь не конь — сороконожка
По дороге той ползёт,
Весь обоз один везёт.
Ответ: (Паровоз )
***
На рояль я не похожий,
Но педаль имею тоже
Кто не трус и не трусиха
Прокачу того я лихо
У меня мотора нет
Я зовусь.
Ответ: (Велосипед )
***
Я зашел в зеленый дом
И недолго пробыл в нем.
Оказался этот дом
Быстро в городе другом.
Ответ: (Вагон )
***
Едет конь стальной, рычит,
Сзади плуги волочит.
Ответ: (Трактор )
***
И катком, и бороною
Он в полях наводит гладь.
И лежат они весною,
Словно в клеточку тетрадь.
Ответ: (Трактор )
***
Не летает, не жужжит,
Жук по улице бежит.
И горят в глазах жука
Два слепящих огонька.
Ответ: (Автомобиль )
***
Если б встала, до неба достала б.
Ответ: (Дорога )
***
Опоясал каменный ремень
Сотни городов и деревень.
Ответ: (Дорога )
***
Летит птица-небылица,
А внутри народ сидит,
Меж собою говорит.
Ответ: (Самолёт )
***
Что за птица:
Песен не поёт, гнезда не вьёт,
Людей и груз несёт?
Ответ: (Вертолёт, Самолёт )
***
Летит стрекоза,
Шумит как гроза.
Ответ: (Вертолёт )
***
Два убегают, два догоняют, а отдыхают вместе.
Ответ: (Четыре колеса машины )
***
Четыре брата бегут —
Друг друга не догонят.
Ответ: (Колёса )
***
Там, где строят новый дом,
Ходит воин со щитом.
Где пройдёт он, станет гладко,
Будет ровная площадка.
Ответ: (Бульдозер )
***
Великан стоит в порту,
Освещая темноту,
И сигналит кораблям:
«Заходите в гости к нам!»
Ответ: (Маяк )
***
Им в морях всегда почёт,
Их девиз: всегда вперёд!
Если ветер в них подует,
То корабль быстрей плывёт.
Ответ: (Паруса )
***
На море, в реках и озерах
Я плаваю, проворный и скорый.
Среди военных кораблей
Известен легкостью своей.
Ответ: (Катер )
***
Плывет белый гусь —
Брюхо деревянное,
Крыло полотняное.
Ответ: (Яхта )
***
Ходит город-великан
На работу в океан.
Ответ: (Корабль )
***
Над рекой, поперек,
Великан врастяжку лег.
Через реку по спине
Он ходить позволил мне.
Ответ: (Мост )
***
На пробитое колесо обычно указывает посторонний шум снаружи, а также потеря скорости и ухудшение управляемости. Если машину уводит в сторону, а чтобы удержать её на дороге, приходится прилагать усилия, то, скорее всего, прокол на одном из передних колёс. Если же заносить начинает заднюю часть авто, то проблема именно там.
Когда это случится, вы точно поймёте, в чём дело. Ни в коем случае не паникуйте. Выровняйте автомобиль и, постепенно снижая скорость, съезжайте на обочину.
Как поменять колесо
1. Припаркуйтесь на обочине
Продолжать движение с проколотой шиной нельзя, но и останавливаться посреди дороги тоже не дело. Поэтому не бойтесь проехать пару десятков метров и выберите ровное сухое место на обочине.
Водителям машин с механической коробкой передач нужно обязательно включить первую передачу, а владельцам автоматики — перевести рычаг в положение паркинга (P).
И в любом случае нужно поставить машину на ручник.
2. Установите знак аварийной остановки и подготовьте инструменты
Припарковав машину в безопасном месте, не забудьте включить аварийную сигнализацию и установить знак аварийной остановки, который находится в багажнике. В населённых пунктах его ставят в 20 метрах позади авто, а на трассе — в 40 метрах.
Там же, в багажнике, найдите запаску и домкрат с баллонным ключом. Обычно производитель располагает всё это в специальной нише под поликом, куда можно добраться, приподняв нижнюю панель.
Хорошо, если у вас с собой будет насос и манометр для проверки давления, а также противооткатные упоры. Ну и, конечно, не помешают перчатки, поскольку немного испачкать руки всё же придётся.
3. Снимите колесо
Достав все инструменты и запаску, разложите их рядом с пробитым колесом и попросите всех пассажиров выйти из машины. Даже если на улице или проливной дождь, безопасность прежде всего.
Несмотря на ручник и включённую передачу, перед установкой домкрата нужно дополнительно зафиксировать колёса с помощью упоров. За них, впрочем, сойдут любые камни или куски кирпича.
Если нужно заменить заднее колесо, упоры ставятся с обеих сторон передних колёс, и наоборот.
Теперь можно приступать к снятию колеса. Сначала освободите диск от пластикового колпака и с помощью баллонного ключа ослабьте болты. Чтобы сдвинуть их с места, понадобится большое усилие, которое можно обеспечить весом своего тела, просто надавив на ключ ногой. Полностью выкручивать болты не надо: достаточно вывернуть их на один оборот.
После этого нужно поднять машину домкратом. Устанавливать его куда попало ни в коем случае нельзя. Специально для этих целей на днище есть небольшие усиленные места, которые обычно находятся позади переднего колеса или сразу перед задним. Производитель обозначает их с помощью треугольников или вырезов внизу порогов. Если сварной шов закрыт пластиковыми накладками, то они будут прерываться в точках установки домкрата.
Подведите домкрат под днище и начните крутить его рукоятку по часовой стрелке. Обязательно следите, чтобы домкрат поднимался ровно, не кренился.
Если под весом машины нижняя лапа домкрата уходит в грунт, нужно подложить под неё что-то вроде куска доски или кирпича.
Слишком поднимать колесо не стоит. Достаточно остановиться в 5 см от земли. После этого можно полностью вывернуть болты и снять пробитое колесо со ступицы. Его лучше задвинуть под машину в качестве страховки, а болты сложить куда-нибудь на тряпочку, чтобы не потерялись.
4. Установите и проверьте запаску
Осталось поставить вместо проколотого колеса запаску. Для этого совместите отверстия на диске с отверстиями в ступице, наденьте колесо и наживите болты, полностью завернув их от руки.
Гайки, крепящие колёса к ступице, важно установить полукруглой стороной к диску, а не наружу.
Уберите пробитое колесо из-под машины, опустите домкрат и окончательно затяните болты. Делать это нужно правильно. В колёсах с четырьмя или шестью отверстиями попарно затягиваются противоположные болты. Если отверстий пять, то тянуть нужно в таком порядке, будто рисуешь пятиконечную звезду.
Остаётся собрать инструмент, убрать домкрат и упоры, а также проверить давление в установленном колесе и при необходимости подкачать его. Если насоса под рукой нет, можно попросить помощи у проезжающих мимо водителей.
Если используете малогабаритную запаску, так называемую докатку, то не забывайте об осторожности: обычно на ней можно двигаться со скоростью не более 80 км/ч и на расстояние максимум 100 километров.
Ну и, конечно, постарайтесь как можно скорее починить пробитое колесо в специализированном шиномонтаже, чтобы не испытывать судьбу и не ездить без запаски.
Очень часто приходится слышать фразы типа: «у тебя какого радиуса колеса, пятнадцатого?» Или «у меня радиус 16, но на зиму поставлю семнадцатый, чтоб повыше машина была»… Такие слова можно услышать как из уст людей, далеких от автомобилей, так и от «как бы профессионалов», вроде работников шиномонтажа или менеджеров по продажам в автосалоне.
Некоторые вещи нудно звучат и трудно запоминаются, но знать их нужно. Особенно автолюбителям. Особенно считающим себя специалистами и имеющим по любому поводу собственное мнение. Дьявол кроется в мелочах, и как раз об одной такой мелочи эта статья.
Не бывает у шины радиуса
Многие сейчас даже не поймут, к чему я клоню. «Ну, радиус, и что? У меня вот колеса 195-65R15, радиус 15, все ж написано, че ты умничаешь?!» Вот то, что умничаю. R15 к радиусу никакого отношения не имеет. Ни R, ни 15.
Сейчас в интернете можно найти массу информации, только такие мелочи, как маркировка автомобильных покрышек, не относятся к самым востребованным. Мы лучше пообсуждаем мощность двигателя или количество «плюшек» в салоне, да? А выбор колес оставим менеджеру в магазине. Ну или у друга спросим. Он-то точно в курсе! У него уже третья машина!
На самом деле, разбираться в этих скучных цифрах не помешает даже просто для общего развития. Тем более, что это и сэкономить поможет, и на поведение машины повлиять, но об этом позже. Пока что — чистый ликбез, дабы потом можно было хорошо понимать друг друга.
Итак, 195/65R15. Классический случай. Присядем на корточки возле своего автомобиля. Первая цифра — это ширина беговой части покрышки, грубо говоря, ширина протектора. Выражается в миллиметрах. То есть 195 мм. — это ширина вашего колеса. С пониманием этой цифры у большинства проблем нет.
Через дробь 65 — это величина профиля. Выражается в процентах от ширины. Не в миллиметрах! Профиль — это часть покрышки, «торчащая над диском». Боковина. То есть, высота этой боковины будет 195х65%=125,75 мм. А не 65 мм. И не что-то еще. Более того, из этой схемы однозначно следует, что высота 65% при ширине 195 будет одна, а если покрышка с маркировкой (условно) 225/65R15 — уже совсем другая! 225х65%=146,25 мм. Хотя цифры 65 — одинаковые!
R — это радиальная конструкция шины, а точнее, способ укладки металлического корда внутри нее. Когда-то конструкция шины предполагала диагональную укладку, но это было давно. Сейчас «диагональных» шин уже почти не встретишь, все сплошь радиальные, и буква R никому ничего нового не сообщит, только споры о пресловутом радиусе вызовет…
Ну и, наконец, цифра 15. Это диаметр. Диаметр посадочной части покрышки, внутренний диаметр, та часть, которая с диском соприкасается. Выражается в дюймах. 1 дюйм = 2,54 см. То есть 15х2,54=38,1 см Это еще и наружный диаметр диска, если кто не догадался…
Какие шины можно ставить, а какие нельзя?
А дальше начинается самое интересное. Мы можем играть этими цифрами, если хотим поставить на машину другие шины (диски). В идеале, главное — чтобы общий диаметр не отличался, либо отличался незначительно. Пример.
Колесо 195/65R15 имеет вот такой общий диаметр: 38,1 см — внутри, плюс 125,75 мм х2 = 251,5 мм (профиль же и сверху, и снизу есть). Переведем в сантиметры для простоты, получится 38,1 см+25,15 см=63,25 см. Вот как! Это и есть диаметр колеса в сумме.
Теперь при желании поставить другие колеса владелец автомобиля должен понимать следующее: эту цифру автопроизводители понимают так же, как и мы. Учитывая диаметр колеса, проектируется подвеска, тормозная система и кузов. Поэтому для одной и той же модели автомобиля (например, для Фольксваген Поло седан) официально допустимы три размерности колес. Самая простая версия довольствуется 175/70R14 (общий диаметр 60,06 см), 185/60R15 (60,3 см) и 195/55R15 (59,55 см).
Получается, что «колесо на 14» БОЛЬШЕ, пусть и незначительно, чем колесо на 15 в случае 195/55. Это к вопросу, затронутому выше, о том, чтоб на зиму колеса побольше поставить… Нужно все внимательно посчитать. Будет ли большая цифра диаметра означать и больший размер колеса в целом? Далеко не всегда.
Парадокс Монти Холла (объяснение)
Я думаю, большая часть из вас, дорогие пикабушники, слышала об этом парадоксе, который по сути-то и не является настоящим парадоксом. Он назван так только потому, что простая человеческая интуиция никак не может принять обоснованный логический ответ и упорно сопротивляется. В этом посте я хотел бы рассказать об этом парадоксе тем, кто о нем не слышал, и постараться объяснить на пальцах, почему решение именно такое.
Ну что ж, начнем с самой формулировки:
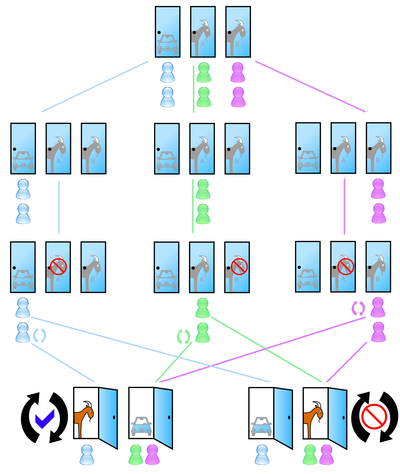
«Представьте, что вы стали участником игры, в которой вам нужно выбрать одну из трёх дверей. За одной из дверей находится автомобиль, за двумя другими дверями — козы. Вы выбираете одну из дверей, например, номер 1, после этого ведущий, который знает, где находится автомобиль, а где — козы, открывает одну из оставшихся дверей, например, номер 3, за которой находится коза. После этого он спрашивает вас — не желаете ли вы изменить свой выбор и выбрать дверь номер 2? Увеличатся ли ваши шансы выиграть автомобиль, если вы примете предложение ведущего и измените свой выбор?»
Сначала попробуйте подумать сами над этой задачей и прийти к ответу.
Многие отвечают, что если изменить выбор двери, то ничего изменится, т.к. дверей осталось всего две, то есть вероятность выигрыша 50 на 50. Но это неверный ответ. Правильный ответ таков, что при смене двери шансы выиграть автомобиль увеличиваются аж в 2 РАЗА! Однако, казалось бы, почему если в конце произвольный выбор из двух дверей, то вероятность должна быть не 50 на 50? А все потому, что от начального выбора двери (когда их 3 закрытых),и будет зависеть то, какая дверь будет выбрана в конце.
Давай-те же теперь подробно разберемся, почему так происходит.
1)Предположим, что в начале игрок выбрал дверь с автомобилем (вероятность этого 1/3)
а)Игрок не меняет дверь, он выиграл АВТОМОБИЛЬ! (+)
б)Игрок меняет дверь и уходит домой с одной козой :(( (-)
2)Предположим, что в начале игрок выбрал дверь с козой (вероятность этого 2/3)
а)Игрок не меняет дверь и, опечалившись, уходит домой с козой (-)
б)Игрок меняет дверь и радостный уезжает на АВТОМОБИЛЕ домой (+)
Посмотрев на все возможные варианты развития событий, можно заметить, что при смене двери игрок уходит с козой, только если изначально была выбрана верная дверь, вероятность чего 1/3, а в ином случае с вероятность 2/3, он забирает ключи и валит из этого заведения на новенькой (или не очень) машине.
Ну вот и все, надеюсь Вам было интересно и понятно, что я написал. Также надеюсь, что Вам стал понятен ответ в этой вызывающей споры и большие дискуссии задаче 🙂
Всем пока и удачного дня)
P.s. Мой первый пост, однако судите, как хотите. Мне не нужны все эти «судите не строго», мне нужна конструктивная критика.
Вероятность попадания 1-1/3=2/3. И никаких парадоксов.
У меня делема по поводу тех трех дверей. Действительно вероятность успеха при смене двери повышается в 2 раза, но зато вероятность неудачи при условии того что дверь не меняется падает в 2 раза.
Ну если на выбор 10 дверей. За одной дверью приз, за остальными нет. Вы указываете на одну дверь. Ведущий открывает оставшиеся 8 неверных дверей, кроме одной.
То это сразу понятно. А с тремя дверьми надо считать уже.
Не поверю, пока сам не проверю!
разрушители мифов по этому поводу наглядный эксперимент проводили. Очень убедительный
хоть и баян но я все равноне догоняяяюююююююююююююю
Так менять или нет. Объясни!
9l c4uTalO 4To Hy>l
Я понял =) попробую объяснить тем кто ещё не вшаривает.
Ведущий, точно зная где машина выбрал ту ячейку в которой осел и не выбрал ту которую выбрал игрок.
Проще говоря выбор во второй раз предлагают только тому кто заведомо выбрал неверный вариант!
В фильме «21» хорошо рассказано
Если вам предложат много раз выбирать и менять решение после того как открыли одну дверь, то все верно. Статистически доказано, что в большинстве раз вы будете в выигрыше. Но что будет, если вам предложат выбирать, и менять или не менять решение лишь один раз?
Вы ведь по-прежнему не знаете, за какой дверью автомобиль. Вам придется выбирать из двух дверей, а это50/50.
Вероятность
История проблемы равенства классов P и NP
В 2000 году Математический институт Клэя определил 7 математических задач, решение которых не могли найти в течение многих лет. За решение каждой из них была назначена награда в размере 1 миллиона долларов. Эти 7 задач известны как «задачи тысячелетия», и на сегодняшний день только одна из них была решена — гипотеза Пуанкаре. В этой статье пойдет речь о вопросе равенства классов P и NP, ответ на который может сильно повлиять на всю IT-сферу.
Равенство P и NP классов отсылает нас к теории алгоритмов, а именно к классам сложности. Первое, с чего стоит начать, это то, что классы P и NP классифицируют языки, а не задачи. Пока что это звучит довольно абсурдно, поэтому для понимания разберемся в некоторых деталях.
Пусть А — алфавит и L ⊆ А*, тогда L называется языком над А. Для любого алфавита пустое множество и А* являются тривиальными языками. При этом пустое множество часто называют пустым языком. Однако не стоит путать пустой язык и язык, содержащий пустое слово e, — они различны. Языки могут быть как бесконечными, так и нет, но обязательно счетными. Т. е. множество всех действительных чисел языком нельзя назвать, т. к. такой набор является неисчисляемым.
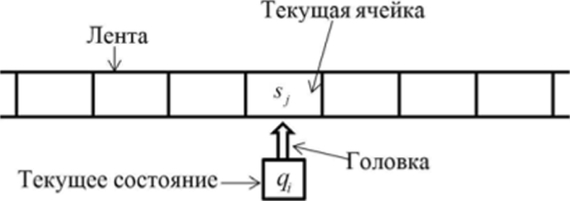
Говоря про абстрактный исполнитель, чаще всего имеют в виду машину Тьюринга, поэтому в дальнейшем под АИ будем подразумевать именно её. Итак, машина Тьюринга имеет неограниченное линейное хранилище, сгруппированное в ячейки. Каждая ячейка может содержать ровно один символ алфавита в любой момент времени. Вдоль ячеек идет считывающая головка, имеющая конечное число состояний. За одну итерацию она может считать значение только одной ячейки, переписать её значение, изменить свое состояние и перейти на одну позицию вправо/влево.
Устройство машины Тьюринга
На основе машины Тьюринга определим так называемую разрешающую машину над языком. Для начала введем определение характеризующей функции X(w). Функция X определяет, принадлежит ли слово w языку L. Если да, то значение функции равно «1»; если нет, то «0». Формально это можно записать так:
Разрешающей машиной D для языка L называется такая машина, которая для каждого w∈A вычисляет характеризующую функцию X(w) за конечное время.
В дополнение к разрешающей машине идет верификатор. Машина V, которая принимает слова w и c и выводит 0 или 1 после конечного числа шагов, называется верификатором для L, если она обладает следующими свойствами:
— выводит 1, только если w входит в язык L;
— для любого w в языке L существует такое c, что V(w,c) = 1.
Классы сложности и формулировка проблемы
Окей, мы рассмотрели несколько понятий. На первый взгляд, все это больше походит на лингвистику: алфавиты, слова, языки… Причем тут задачи? Чтобы ответить на этот вопрос, обратимся к понятию задача разрешимости (англ. Decision problem). Это такой вопрос (сформулированный в формальной системе), требующий ответа «да» или «нет», зависящего, возможно, от значений некоторых входных параметров. Например, «является ли данное натуральное число x простым?» или «даны два числа: x и y; делится ли x на y?« Метод решения в виде алгоритма называется разрешающей процедурой. Теория вычислимости имеет дело в основном с задачами разрешимости и приведенные выше конструкции наглядно соотносятся с таким типом задач: так разрешающая машина над языком является формализацией разрешающей процедуры. Но как же быть с задачами, такими как задача коммивояжера? На них нельзя дать бинарный ответ. В таких случаях применяют приемы приведения к версии decision problem. В случае коммивояжера проблема по-новому формулируется так: «существует ли маршрут не длиннее, чем заданное значение k?»
В класс сложности NP входят все языки L, для которых существует такой верификатор, что для каждого (w,c) время его работы полиномиально. Иными словами, NP включает в себя задачи разрешимости, для которых при подходящем сертификате для данного w мы быстро сможем удостовериться в том, что w действительно принадлежит L (ответ на вопрос можно довольно быстро проверить). Отсюда и название «верификатор». В качестве примера задачи в NP можно привести определение наличия в графе гамильтонова цикла. Сертификат в данном случае — последовательность вершин, образующих гамильтонов цикл.
Помимо этих классов можно выделить ещё 2: NP-hard и NP-Complete. Они основываются на приводимости одного языка к другому за полиномиальное время: пусть языки A и B — языки над одним алфавитом. Язык А будет приводимым за полиномиальное время к языку B, если существует такая функция f(w), что
— функция f может быть вычислена машиной Тьюринга за полиномиальное время.
Тогда в класс NP-hard будут входить языки, к которым приводимы все языки в NP (причем NP-hard язык может входить в NP, а может и нет), а в NP-Complete те языки, которые являются одновременно NP-hard и NP. Примером NP-Complete является язык выполнимых булевых формул (SAT). Таким образом, NP-Complete задачи образуют в некотором смысле подмножество «типовых» задач в классе NP: если для какой-то из них найден «полиномиально быстрый» алгоритм решения, то и любая другая задача из класса NP может быть решена так же «быстро».
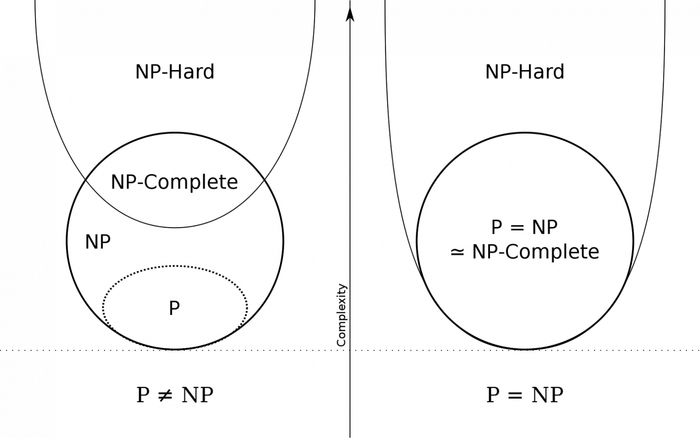
Отношение между классами при равенстве и неравенстве
Теперь, немного погрузившись в теорию алгоритмов, более конкретно обозначим проблему равенства данных классов. Итак, множество P входит в множество NP, но неизвестно, существуют ли языки, которые входят в NP и не входят в P. Что это означает на практике? Итак, простыми словами класс NP можно охарактеризовать как «трудно решить, легко проверить». Классическим примером задачи, входящей в NP, является задача коммивояжера, для решения которой на данный момент известен лишь один алгоритм — старый добрый перебор (мы не рассматриваем эвристические методы). Однако, получив ответ, его будет не так сложно проверить. Класс P же вобрал в себя те задачи, для которых существует эффективный алгоритм решения, позволяющий решать их за полиномиальное время. И равенство или, наоборот, неравенство этих классов пока не доказано. Если эти классы равны, то это будет значить, что для всех задач, которые сейчас решаются путем перебора или другим неэффективным методом, существует(-ют) полиномиальные алгоритмы. А если не равны, то придется смириться с неоптимальностью решения этих задач.
История проблемы равенства P и NP началась в 1928 году, когда Давид Гильберт сформулировал проблему, названную Entscheidungsproblem (нем. задача разрешения). Ее суть заключается в нахождении алгоритма, определяющего доказуемость данного утверждения из аксиом с использованием правил логики. По названию очевидно, что это задача является задачей разрешения (выводит «да» или «нет»).
В ходе решения этой проблемы потребовалось определить термины «алгоритм» и «вычислимая функция». В 1936 году Алонзо Чёрч и Алан Тьюринг независимо показали, что общее решение Entscheidungsproblem невозможно, предположив, что интуитивное понятие «эффективная вычислимость» соответствует вычислимости функции на машине Тьюринга. Эта гипотеза сегодня известна как тезис Чёрча-Тьюринга.
20 марта 1956 в письме к Джону фон Нейману Курт Гёдель впервые поставил вопрос о вычислительной сложности. Гёдель интересовался, можно ли получить доказательство теоремы (в математико-логическом смысле слова) за квадратичное или линейное время. К сожалению, письмо было обнаружено лишь в 1989 году и получило широкую огласку, когда Юрис Хартманис опубликовал перевод и комментарий.
Статья Алана Кобэма 1965 года под названием «The intrinsic computational difficulty of functions» является одним из первых упоминаний класса сложности P, состоящего из разрешимых за полиномиальное время задач. Тезис Кобэма-Эдмондса (известный также как расширенный тезис Чёрча-Тьюринга), названный в честь Алана Кобэма и Джека Эдмондса, утверждает, что любая разумная модель вычислений может быть выражена через другую модель с замедлением, не более чем полиномиальным по размеру входных данных. Кобэм предположил, что класс P может быть хорошим способом для описания множества реально вычислимых задач. Любая проблема, не содержащаяся в P, невозможна, но если задача реального мира может быть решена с помощью алгоритма, существующего в P, то такой алгоритм в конечном итоге будет открыт.
В 1965 году Юрис Хартманис и Ричард Стернс опубликовали статью «On the Computational Complexity of Algorithms», отмеченную премией Тьюринга. В ней даются более точные определения сложности алгоритма и класса сложности. Хартманис и Стернс определили класс сложности как совокупность всех задач, которые можно решить за установленные временные рамки. В их статье показано, что существует бесконечная иерархия классов сложности (например, задачи, для которых наиболее быстрый алгоритм имеет время, пропорциональное n, n log n, n^2, n^3, 2^n и т. д.), где небольшое увеличение временного интервала позволяет решать больше задач. Во второй статье Хартманис совместно с Филипом М. Льюисом показали, что подобная иерархия существует и для количества памяти (функция от размера входа) при решении задачи на машине Тьюринга.
В 1967 году Мануэль Блюм разработал аксиоматическую теорию сложности, которая основана на его собственных аксиомах (аксиомы Блюма), и получил важный результат — теорему об ускорении. До этого мы говорили по большей части о сложности алгоритма. Хотелось бы аналогичным образом определить и сложность задачи: например, какова сложность самого эффективного (по времени и емкости) алгоритма, решающего эту задачу. Теорема об ускорении гласит, что есть некоторые задачи, для которых не существует самого быстрого алгоритма, потому что любой алгоритм для такой задачи можно «ускорить», построив более быстрый алгоритм.
Точная формулировка проблемы равенства P и NP была представлена в 1971 году. Тогда американский ученый Стивен Кук и работавший независимо советский ученый Леонид Левин доказали, что существуют практически актуальные проблемы, которые являются NP-полными. В США Стивен Кук опубликовал статью «The complexity of theorem proving procedures», в которой формализовал понятия редукции за полиномиальное время и NP-полноты, а также доказал существование NP-полной задачи (задача выполнимости булевых формул, SAT). Теорема была независимо доказана Леонидом Левиным и, таким образом, получила название «теорема Кука-Левина».
В 1972 году Ричард Карп сделал рывок в знаменитой статье «Reducibility among Combinatorial Problems», в которой показал, что около 20 разнообразных задач из комбинаторики и теории графов, известных своей вычислительной трудностью, являются NP-полными.
В августе 2010 года Виней Деолаликар, работавший в исследовательском отделении Hewlett-Packard в Пало-Альто в Калифорнии, заявил, что разгадал загадку P vs NP. Он утверждал, что P не равняется NP, однако научное сообщество нашло в его доказательстве фатальную ошибку. В начале 2002 года SIGACT News провел опрос среди 100 ученых, задав им вопрос о равенстве классов NP и P. 61 человек ответили, что «неравны», 9 — «равны», 22 затруднились ответить и 8 сказали, что гипотеза не выводима из текущей системы аксиом и, таким образом, не может быть доказана или опровергнута.
К чему приведет решение проблемы
Окей, теория вычислимости, формализация алгоритмов и абстрактные математические теории — все это конечно интересно, но как решение проблемы равенства NP и P классов отразится на практике? На самом деле, алгоритмы для решения NP-задач используются каждый день во многих сферах. Например, в криптографии, криптовалютах, восстановлении поврежденных файлов, системах блокировки спама, оптимизации в логистике и т. д. Более эффективные решения могли бы значительно сэкономить время и деньги, так как мы пользуемся в основном эвристическими методами, дающими лишь приближенные решения.
Однако существует и обратная сторона монеты. Солидная часть криптографии (криптосистемы с открытым ключом, технологии доказательства выполнения работы в блокчейне, системы блокировки спама) основывается на предположении о неравенстве NP и P классов. Если окажется, что некоторые задачи, для которых, как считалось, не существует эффективных алгоритмов, можно решать быстро, то многие методы защиты устареют.
Может оказаться и так, что последствия решения окажутся не такими тривиальными, как это часто и бывает в математике. В качестве примера рассмотрим континуум-гипотезу о существовании мощности, меньшей континуума и большей мощности счетного множества. Оказывается, существование такого кардинала нельзя ни доказать, ни опровергнуть в аксиоматике ZFC. Так что мы вправе считать, что такие мощности бывают (впрочем, как и считать, что не бывают). Однако ясно, что мы не можем конструктивно построить соответствующее множество. Возможно, точно также окажется и с алгоритмами для NP-задач в случае равенства NP и P (к слову, некоторые математики в опросе SIGACT News так и ответили: гипотеза не выводима из существующей системы аксиом, то есть не может быть доказана или опровергнута).
Пока что существующих методов доказательств недостаточно для строго математического ответа, но не нужно терять надежду. В марте 2001 года Ричард Карп предсказал, что проблема будет решена молодым математиком (до 30 лет) с использованием подхода, о котором еще никто не думал. Стивен Кук заявил, что кто-нибудь предоставит убедительное доказательство в ближайшие 20 лет.