Арктангенс как найти в треугольнике

sine, left parenthesis, theta, right parenthesis, equals, start fraction, start text, п, р, о, т, и, в, о, л, е, ж, а, щ, и, й, space, к, а, т, е, т, end text, divided by, start text, г, и, п, о, т, е, н, у, з, а, end text, end fraction right arrow a, r, c, s, i, n, left parenthesis, start fraction, start text, п, р, о, т, и, в, о, л, е, ж, а, щ, и, й, space, к, а, т, е, т, end text, divided by, start text, г, и, п, о, т, е, н, у, з, а, end text, end fraction, right parenthesis, equals, theta cosine, left parenthesis, theta, right parenthesis, equals, start fraction, start text, п, р, и, л, е, ж, а, щ, и, й, space, к, а, т, е, т, end text, divided by, start text, г, и, п, о, т, е, н, у, з, а, end text, end fraction right arrow a, r, c, c, o, s, left parenthesis, start fraction, start text, п, р, и, л, е, ж, а, щ, и, й, space, к, а, т, е, т, end text, divided by, start text, г, и, п, о, т, е, н, у, з, а, end text, end fraction, right parenthesis, equals, theta t, g, left parenthesis, theta, right parenthesis, equals, start fraction, start text, п, р, о, т, и, в, о, л, е, ж, а, щ, и, й, space, к, а, т, е, т, end text, divided by, start text, п, р, и, л, е, ж, а, щ, и, й, space, к, а, т, е, т, end text, end fraction right arrow a, r, c, t, g, left parenthesis, start fraction, start text, п, р, о, т, и, в, о, л, е, ж, а, щ, и, й, space, к, а, т, е, т, end text, divided by, start text, п, р, и, л, е, ж, а, щ, и, й, space, к, а, т, е, т, end text, end fraction, right parenthesis, equals, theta
Источник

Укажите размеры:

Результат:

Решение:

Скопировать

Ссылка на страницу с результатом:

# Теория

Прямоугольный треугольник — это геометрическая фигура, образованная тремя отрезками соединяющихся тремя точками, у которой все углы внутренние, при этом один из углов прямой (равен 90°).

β
α

a
b
c

Тангенс угла tg(α) — это тригонометрическая функция выражающая отношение противолежащего катета a к прилежащему катету b.

Формула тангенса

tg alpha = dfrac{a}{b}

  • tg α — тангенс угла α
  • a — противолежащий катет
  • b — прилежащий катет

Арктангенс — это обратная тригонометрическая функция. Арктангенсом числа x называется такое значение угла α, выраженное в радианах, для которого tg α = x. Вычислить арктангенс, означает найти угол α, тангенс которого равен числу x.

Углы треугольника

Сумма углов треугольника всегда равна 180 градусов:

angle alpha + angle beta + angle gamma = 180°

Так как у прямоугольного треугольника один из углов равен 90°, то сумма двух других углов равна 90°.

Поэтому, если известен один из острых углов треугольника, второй угол можно посчитать по формуле:

angle alpha = 90° — angle beta

angle beta = 90° — angle alpha

Острый угол — угол, значение которого меньше 90°.

У прямоугольного треугольника один угол прямой, а два других угла — острые.

Похожие калькуляторы:

Войдите чтобы писать комментарии

Источник
  • Определение

  • График арктангенса

  • Свойства арктангенса

  • Таблица арктангенсов

Определение

Арктангенс (arctg или arctan) – это обратная тригонометрическая функция.

Арктангенс x определяется как функция, обратная к тангенсу x, где x – любое число (x∈ℝ).

Если тангенс угла у равен х (tg y = x), значит арктангенс x равняется y:

arctg x = tg-1 x = y, причем -π/2<y<π/2

Примечание: tg-1x означает обратный тангенс, а не тангенс в степени -1.

Например:

arctg 1 = tg-1 1 = 45° = π/4 рад

График арктангенса

Функция арктангенса пишется как y = arctg (x). График в общем виде выглядит следующим образом:

График арктангенса

Свойства арктангенса

Ниже в табличном виде представлены основные свойства арктангенса с формулами.

Таблица арктангенсов
arctg x (°) arctg x (рад) x
-90° -π/2 -∞
-71.565° -1.2490 -3
-63.435° -1.1071 -2
-60° -π/3 -√3
-45° -π/4 -1
-30° -π/6 -1/√3
-26.565° -0.4636 -0.5
0° 0 0
26.565° 0.4636 0.5
30° π/6 1/√3
45° π/4 1
60° π/3 √3
63.435° 1.1071 2
71.565° 1.2490 3
90° π/2 ∞

microexcel.ru

Источник
При решении геодезических и инженерных задач, очень часто приходиться вспоминать и искать необходимые формулы. В связи с этим хочется представить Вам шпаргалку (назовем её “геодезической шпаргалкой”:)), в которой приведены часто использующиеся формулы.
Конечно, ее содержание не охватывает всю высшую математику или сферическую геометрию, но что-нибудь должно пригодиться.
Зная из собственного опыта, неудобство восприятия формул без чисел, к каждой из них приводится пример вычисления.

Теорема Пифагора

Пример вычислений теорема Пифагора

Соотношения в прямоугольном треугольнике

Пример вычислений соотношения в прямоугольном треугольнике

Обратные тригонометрические функции арксинус (arcsin), арккосинус (arccos), арктангенс (arctg) и арккотангенс (arcctg)

— арксинус (arcsin) возвращает угол по его синусу

— арккосинус (arccos) возвращает угол по его косинусу

— арктангенс (arctg) возвращает угол по его тангенсу

— арккотангенс (arcctg) возвращает угол по его арктангенсу

Пример вычислений обратные тригонометрические функции

Сумма углов треугольника

Сумма углов в треугольнике равна 180 градусам

Теорема синусов

Для любого треугольника соблюдается выражение

Пример вычислений теорема синусов

Теорема косинусов

Квадрат любой стороны треугольника, равен сумме квадратов двух других его сторон, минус удвоенное произведение этих сторон на косинус угла между ними

Пример вычислений теорема косинусов

Площадь треугольника

Площадь треугольника можно определить по формулам

также удобно использовать формулу Герона ,
где p-полупериметр треугольника

Пример вычислений площадь треугольника

или по формуле Герона

Площадь круга

Длина дуги окружности

Длина дуги окружности вычисляется по формулам

если угол задан в угловых градусах минутах и секундах

если угол задан в радианах

Пример вычислений длина дуги окружности

угол задан в угловых градусах минутах и секундах

угол задан в радианах

Перевод градусов в угловые градусы минуты и секунды

Перевод угловых градусов минут и секунд в градусы выполняется согласно выражения

Пример вычислений
перевести в градусы угол, который задан в угловых градусах минутах и секундах


Перевод градусов в угловые градусы минуты и секунды

Перевод градусов в угловые градусы минуты и секунды выполняется согласно выражения

Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в градусах


Перевод градусов в радианы

Перевод градусов в радианы выполняется по формуле

Пример вычислений
перевести в радианы угол, который задан в угловых градусах минутах и секундах


Перевод радианов в градусы

Перевод радианов в градусы выполняется по формуле

Пример вычислений
перевести в угловые градусы минуты и секунды угол, который задан в радианах


Определение наклона линии в градусах

Определение наклона линии в градусах выполняется с использованием соотношений в прямоугольном треугольнике
Пример вычислений
Определить наклон пандуса длиной 14м и высотой 3,5м

Определение уклона линии в долях, процентах и промилле

При инженерно-строительных работах, наклон линии задают не градусом наклона, а тангенсом этого градуса — безразмерной величиной, которая называется уклоном. Уклон может выражаться относительным числом, в процентах (сотые доли числа) и промилле (тысячные доли числа)

Пример вычислений
Определить уклон отмостки длиной 2,5м и высотой 0,30м

Источник

In mathematics, the inverse trigonometric functions (occasionally also called arcus functions,[1][2][3][4][5] antitrigonometric functions[6] or cyclometric functions[7][8][9]) are the inverse functions of the trigonometric functions (with suitably restricted domains). Specifically, they are the inverses of the sine, cosine, tangent, cotangent, secant, and cosecant functions,[10] and are used to obtain an angle from any of the angle’s trigonometric ratios. Inverse trigonometric functions are widely used in engineering, navigation, physics, and geometry.

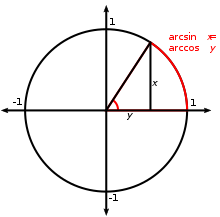
Notation[edit]

For a circle of radius 1, arcsin and arccos are the lengths of actual arcs determined by the quantities in question.

Several notations for the inverse trigonometric functions exist. The most common convention is to name inverse trigonometric functions using an arc- prefix: arcsin(x), arccos(x), arctan(x), etc.[6] (This convention is used throughout this article.) This notation arises from the following geometric relationships:[citation needed]
when measuring in radians, an angle of θ radians will correspond to an arc whose length is rθ, where r is the radius of the circle. Thus in the unit circle, «the arc whose cosine is x» is the same as «the angle whose cosine is x«, because the length of the arc of the circle in radii is the same as the measurement of the angle in radians.[11] In computer programming languages, the inverse trigonometric functions are often called by the abbreviated forms asin, acos, atan.[12]

The notations sin−1(x), cos−1(x), tan−1(x), etc., as introduced by John Herschel in 1813,[13][14] are often used as well in English-language sources,[6] much more than the also established sin[−1](x), cos[−1](x), tan[−1](x) – conventions consistent with the notation of an inverse function, that is useful (for example) to define the multivalued version of each inverse trigonometric function: {displaystyle tan ^{-1}(x)={arctan(x)+pi kmid kin mathbb {Z} }~.} However, this might appear to conflict logically with the common semantics for expressions such as sin2(x) (although only sin2 x, without parentheses, is the really common use), which refer to numeric power rather than function composition, and therefore may result in confusion between notation for the reciprocal (multiplicative inverse) and inverse function.[15]

The confusion is somewhat mitigated by the fact that each of the reciprocal trigonometric functions has its own name — for example, (cos(x))−1 = sec(x). Nevertheless, certain authors advise against using it, since it is ambiguous.[6][16] Another precarious convention used by a small number of authors is to use an uppercase first letter, along with a “−1” superscript: Sin−1(x), Cos−1(x), Tan−1(x), etc.[17] Although it is intended to avoid confusion with the reciprocal, which should be represented by sin−1(x), cos−1(x), etc., or, better, by sin−1 x, cos−1 x, etc., it in turn creates yet another major source of ambiguity, especially since many popular high-level programming languages (e.g. Mathematica, and MAGMA) use those very same capitalised representations for the standard trig functions, whereas others (Python, SymPy, NumPy, Matlab, MAPLE, etc.) use lower-case.

Hence, since 2009, the ISO 80000-2 standard has specified solely the «arc» prefix for the inverse functions.

Basic concepts[edit]

Principal values[edit]

Since none of the six trigonometric functions are one-to-one, they must be restricted in order to have inverse functions. Therefore, the result ranges of the inverse functions are proper (i.e. strict) subsets of the domains of the original functions.

For example, using function in the sense of multivalued functions, just as the square root function y={sqrt {x}} could be defined from {displaystyle y^{2}=x,} the function {displaystyle y=arcsin(x)} is defined so that {displaystyle sin(y)=x.} For a given real number x, with {displaystyle -1leq xleq 1,} there are multiple (in fact, countably infinitely many) numbers y such that {displaystyle sin(y)=x}; for example, {displaystyle sin(0)=0,} but also {displaystyle sin(pi )=0,} {displaystyle sin(2pi )=0,} etc. When only one value is desired, the function may be restricted to its principal branch. With this restriction, for each x in the domain, the expression arcsin(x) will evaluate only to a single value, called its principal value. These properties apply to all the inverse trigonometric functions.

The principal inverses are listed in the following table.

Name Usual notation Definition Domain of x for real result Range of usual principal value
(radians) 		Range of usual principal value
(degrees)
arcsine {displaystyle y=arcsin(x)} x = sin(y) {displaystyle -1leq xleq 1} {displaystyle -{frac {pi }{2}}leq yleq {frac {pi }{2}}} {displaystyle -90^{circ }leq yleq 90^{circ }}
arccosine {displaystyle y=arccos(x)} x = cos(y) {displaystyle -1leq xleq 1} {displaystyle 0leq yleq pi } {displaystyle 0^{circ }leq yleq 180^{circ }}
arctangent {displaystyle y=arctan(x)} x = tan(y) all real numbers {displaystyle -{frac {pi }{2}}<y<{frac {pi }{2}}} {displaystyle -90^{circ }<y<90^{circ }}
arccotangent {displaystyle y=operatorname {arccot}(x)} x = cot(y) all real numbers {displaystyle 0<y<pi } {displaystyle 0^{circ }<y<180^{circ }}
arcsecant {displaystyle y=operatorname {arcsec}(x)} x = sec(y) {displaystyle {leftvert xrightvert }geq 1} {displaystyle 0leq y<{frac {pi }{2}}{text{ or }}{frac {pi }{2}}<yleq pi } {displaystyle 0^{circ }leq y<90^{circ }{text{ or }}90^{circ }<yleq 180^{circ }}
arccosecant {displaystyle y=operatorname {arccsc}(x)} x = csc(y) {displaystyle {leftvert xrightvert }geq 1} {displaystyle -{frac {pi }{2}}leq y<0{text{ or }}0<yleq {frac {pi }{2}}} {displaystyle -90^{circ }leq y<0^{circ }{text{ or }}0^{circ }<yleq 90^{circ }}

Note: Some authors[citation needed] define the range of arcsecant to be {textstyle (0leq y<{frac {pi }{2}}{text{ or }}pi leq y<{frac {3pi }{2}})}, because the tangent function is nonnegative on this domain. This makes some computations more consistent. For example, using this range, {displaystyle tan(operatorname {arcsec}(x))={sqrt {x^{2}-1}},} whereas with the range {textstyle (0leq y<{frac {pi }{2}}{text{ or }}{frac {pi }{2}}<yleq pi )}, we would have to write {displaystyle tan(operatorname {arcsec}(x))=pm {sqrt {x^{2}-1}},} since tangent is nonnegative on {textstyle 0leq y<{frac {pi }{2}},} but nonpositive on {textstyle {frac {pi }{2}}<yleq pi .} For a similar reason, the same authors define the range of arccosecant to be {textstyle (-pi <yleq -{frac {pi }{2}}} or {textstyle 0<yleq {frac {pi }{2}}).}

If x is allowed to be a complex number, then the range of y applies only to its real part.

The table below displays names and domains of the inverse trigonometric functions along with the range of their usual principal values in radians.

Name Symbol Domain Image/Range Inverse
function 		Domain Image of
principal values
sine sin : mathbb {R} to [-1, 1] {displaystyle arcsin } : [-1, 1] to {displaystyle left[-{tfrac {pi }{2}},{tfrac {pi }{2}}right]}
cosine cos : mathbb {R} to [-1, 1] arccos : [-1, 1] to [0,pi ]
tangent tan : {displaystyle pi mathbb {Z} +left(-{tfrac {pi }{2}},{tfrac {pi }{2}}right)} to mathbb {R} arctan : mathbb {R} to {displaystyle left(-{tfrac {pi }{2}},{tfrac {pi }{2}}right)}
cotangent cot : {displaystyle pi mathbb {Z} +(0,pi )} to mathbb {R} operatorname{arccot} : mathbb {R} to {displaystyle (0,pi )}
secant sec : {displaystyle pi mathbb {Z} +left(-{tfrac {pi }{2}},{tfrac {pi }{2}}right)} to {displaystyle mathbb {R} setminus (-1,1)} {displaystyle operatorname {arcsec} } : {displaystyle mathbb {R} setminus (-1,1)} to {displaystyle [,0,;pi ,];;;setminus left{{tfrac {pi }{2}}right}}
cosecant csc : {displaystyle pi mathbb {Z} +(0,pi )} to {displaystyle mathbb {R} setminus (-1,1)} {displaystyle operatorname {arccsc} } : {displaystyle mathbb {R} setminus (-1,1)} to {displaystyle left[-{tfrac {pi }{2}},{tfrac {pi }{2}}right]setminus {0}}

The symbol {displaystyle mathbb {R} =(-infty ,infty )} denotes the set of all real numbers and {displaystyle mathbb {Z} ={ldots ,,-2,,-1,,0,,1,,2,,ldots }} denotes the set of all integers. The set of all integer multiples of pi is denoted by

{displaystyle pi mathbb {Z} ~:=~{pi n;:;nin mathbb {Z} }~=~{ldots ,,-2pi ,,-pi ,,0,,pi ,,2pi ,,ldots }.}

The symbol {displaystyle ,setminus ,} denotes set subtraction so that, for instance, {displaystyle mathbb {R} setminus (-1,1)=(-infty ,-1]cup [1,infty )} is the set of points in mathbb {R} (that is, real numbers) that are not in the interval {displaystyle (-1,1).}

The Minkowski sum notation {textstyle pi mathbb {Z} +(0,pi )} and {displaystyle pi mathbb {Z} +{bigl (}{-{tfrac {pi }{2}}},{tfrac {pi }{2}}{bigr )}} that is used above to concisely write the domains of {displaystyle cot ,csc ,tan ,{text{ and }}sec } is now explained.

Domain of cotangent cot and cosecant csc :
The domains of {displaystyle ,cot ,} and {displaystyle ,csc ,} are the same. They are the set of all angles theta at which {displaystyle sin theta neq 0,} i.e. all real numbers that are not of the form {displaystyle pi n} for some integer {displaystyle n,}

{displaystyle {begin{aligned}pi mathbb {Z} +(0,pi )&=cdots cup (-2pi ,-pi )cup (-pi ,0)cup (0,pi )cup (pi ,2pi )cup cdots \&=mathbb {R} setminus pi mathbb {Z} end{aligned}}}

Domain of tangent tan and secant sec :
The domains of {displaystyle ,tan ,} and {displaystyle ,sec ,} are the same. They are the set of all angles theta at which {displaystyle cos theta neq 0,}

{displaystyle {begin{aligned}pi mathbb {Z} +left(-{tfrac {pi }{2}},{tfrac {pi }{2}}right)&=cdots cup {bigl (}{-{tfrac {3pi }{2}}},{-{tfrac {pi }{2}}}{bigr )}cup {bigl (}{-{tfrac {pi }{2}}},{tfrac {pi }{2}}{bigr )}cup {bigl (}{tfrac {pi }{2}},{tfrac {3pi }{2}}{bigr )}cup cdots \&=mathbb {R} setminus left({tfrac {pi }{2}}+pi mathbb {Z} right)\end{aligned}}}

Solutions to elementary trigonometric equations[edit]

Each of the trigonometric functions is periodic in the real part of its argument, running through all its values twice in each interval of 2pi :

This periodicity is reflected in the general inverses, where k is some integer.

The following table shows how inverse trigonometric functions may be used to solve equalities involving the six standard trigonometric functions.
It is assumed that the given values theta , r, s, x, and y all lie within appropriate ranges so that the relevant expressions below are well-defined.
Note that «for some {displaystyle kin mathbb {Z} }» is just another way of saying «for some integer k.»

The symbol {displaystyle ,iff ,} is logical equality. The expression «LHS {displaystyle ,iff ,} RHS» indicates that either (a) the left hand side (i.e. LHS) and right hand side (i.e. RHS) are both true, or else (b) the left hand side and right hand side are both false; there is no option (c) (e.g. it is not possible for the LHS statement to be true and also simultaneously for the RHS statement to false), because otherwise «LHS {displaystyle ,iff ,} RHS» would not have been written (see this footnote[note 1] for an example illustrating this concept).

Equation if and only if Solution Expanded form of solution where…
{displaystyle sin theta =y} iff {displaystyle theta =,} (-1)^{k} {displaystyle arcsin(y)} + {displaystyle pi k} for some {displaystyle kin mathbb {Z} } iff {displaystyle theta =;;;,arcsin(y)+2pi h}           or
{displaystyle theta =-arcsin(y)+2pi h+pi } 		for some {displaystyle hin mathbb {Z} }
{displaystyle csc theta =r} iff {displaystyle theta =,} (-1)^{k} {displaystyle operatorname {arccsc}(r)} + {displaystyle pi k} for some {displaystyle kin mathbb {Z} } iff {displaystyle theta =;;;,operatorname {arccsc}(y)+2pi h}           or
{displaystyle theta =-operatorname {arccsc}(y)+2pi h+pi } 		for some {displaystyle hin mathbb {Z} }
{displaystyle cos theta =x} iff {displaystyle theta =,} {displaystyle pm ,} arccos(x) + 2 {displaystyle pi k} for some {displaystyle kin mathbb {Z} } iff {displaystyle theta =;;;,arccos(y)+2pi h}          or
{displaystyle theta =-arccos(y)+2pi h} 		for some {displaystyle hin mathbb {Z} }
{displaystyle sec theta =r} iff {displaystyle theta =,} {displaystyle pm ,} {displaystyle operatorname {arcsec}(r)} + 2 {displaystyle pi k} for some {displaystyle kin mathbb {Z} } iff {displaystyle theta =;;;,operatorname {arcsec}(y)+2pi h}          or
{displaystyle theta =-operatorname {arcsec}(y)+2pi h} 		for some {displaystyle hin mathbb {Z} }
{displaystyle tan theta =s} iff {displaystyle theta =,} {displaystyle arctan(s)} + {displaystyle pi k} for some {displaystyle kin mathbb {Z} }
{displaystyle cot theta =r} iff {displaystyle theta =,} {displaystyle operatorname {arccot}(r)} + {displaystyle pi k} for some {displaystyle kin mathbb {Z} }

For example, if {displaystyle cos theta =-1} then {displaystyle theta =pi +2pi k=-pi +2pi (1+k)} for some {displaystyle kin mathbb {Z} .} While if {displaystyle sin theta =pm 1} then {textstyle theta ={frac {pi }{2}}+pi k=-{frac {pi }{2}}+pi (k+1)} for some {displaystyle kin mathbb {Z} ,} where k will be even if {displaystyle sin theta =1} and it will be odd if {displaystyle sin theta =-1.} The equations {displaystyle sec theta =-1} and {displaystyle csc theta =pm 1} have the same solutions as {displaystyle cos theta =-1} and {displaystyle sin theta =pm 1,} respectively. In all equations above except for those just solved (i.e. except for sin /{displaystyle csc theta =pm 1} and cos/{displaystyle sec theta =-1}), the integer k in the solution’s formula is uniquely determined by theta (for fixed {displaystyle r,s,x,} and y).

Detailed example and explanation of the «plus or minus» symbol pm

The solutions to {displaystyle cos theta =x} and {displaystyle sec theta =x} involve the «plus or minus» symbol {displaystyle ,pm ,,} whose meaning is now clarified. Only the solution to {displaystyle cos theta =x} will be discussed since the discussion for {displaystyle sec theta =x} is the same.
We are given x between {displaystyle -1leq xleq 1} and we know that there is an angle theta in some interval that satisfies {displaystyle cos theta =x.} We want to find this theta . The table above indicates that the solution is

{displaystyle ,theta =pm arccos x+2pi k,quad {text{ for some }}kin mathbb {Z} }

which is a shorthand way of saying that (at least) one of the following statement is true:

  1. {displaystyle ,theta =arccos x+2pi k,} for some integer k,
    or
  2. {displaystyle ,theta =-arccos x+2pi k,} for some integer k.

As mentioned above, if {displaystyle ,arccos x=pi ,} (which by definition only happens when {displaystyle x=cos pi =-1}) then both statements (1) and (2) hold, although with different values for the integer k: if K is the integer from statement (1), meaning that {displaystyle theta =pi +2pi K} holds, then the integer k for statement (2) is K+1 (because {displaystyle theta =-pi +2pi (1+K)}).
However, if {displaystyle xneq -1} then the integer k is unique and completely determined by theta .
If {displaystyle ,arccos x=0,} (which by definition only happens when {displaystyle x=cos 0=1}) then {displaystyle ,pm arccos x=0,} (because {displaystyle ,+arccos x=+0=0,} and {displaystyle ,-arccos x=-0=0,} so in both cases {displaystyle ,pm arccos x,} is equal to {displaystyle 0}) and so the statements (1) and (2) happen to be identical in this particular case (and so both hold).
Having considered the cases {displaystyle ,arccos x=0,} and {displaystyle ,arccos x=pi ,,} we now focus on the case where {displaystyle ,arccos xneq 0,} and {displaystyle ,arccos xneq pi ,,} So assume this from now on. The solution to {displaystyle cos theta =x} is still

{displaystyle ,theta =pm arccos x+2pi k,quad {text{ for some }}kin mathbb {Z} }

which as before is shorthand for saying that one of statements (1) and (2) is true. However this time, because {displaystyle ,arccos xneq 0,} and {displaystyle ,0<arccos x<pi ,,} statements (1) and (2) are different and furthermore, exactly one of the two equalities holds (not both). Additional information about theta is needed to determine which one holds. For example, suppose that x=0 and that all that is known about theta is that {displaystyle ,-pi leq theta leq pi ,} (and nothing more is known). Then

{displaystyle arccos x=arccos 0={frac {pi }{2}}}

and moreover, in this particular case k=0 (for both the {displaystyle ,+,} case and the {displaystyle ,-,} case) and so consequently,

{displaystyle theta ~=~pm arccos x+2pi k~=~pm left({frac {pi }{2}}right)+2pi (0)~=~pm {frac {pi }{2}}.}

This means that theta could be either {displaystyle ,pi /2,} or {displaystyle ,-pi /2.} Without additional information it is not possible to determine which of these values theta has.
An example of some additional information that could determine the value of theta would be knowing that the angle is above the x-axis (in which case theta =pi /2) or alternatively, knowing that it is below the x-axis (in which case {displaystyle theta =-pi /2}).

Transforming equations

The equations above can be transformed by using the reflection and shift identities:[18]

Argument: {displaystyle {underline {;~~~~~~~~~~~~~~;}}} = {displaystyle -theta } {displaystyle {frac {pi }{2}}pm theta } {displaystyle pi pm theta } {displaystyle {frac {3pi }{2}}pm theta } {displaystyle 2kpi pm theta }, where {displaystyle kin mathbb {Z} }
{displaystyle sin {underline {;~~~~~~~~~~~~~~;}}} = - sin theta   cos theta mp sin theta - cos theta pm sin theta
{displaystyle csc {underline {;~~~~~~~~~~~~~~;}}} = - {displaystyle csc theta }   {displaystyle sec theta } mp {displaystyle csc theta } - {displaystyle sec theta } pm {displaystyle csc theta }
{displaystyle cos {underline {;~~~~~~~~~~~~~~;}}} =   cos theta mp sin theta - cos theta pm sin theta   cos theta
{displaystyle sec {underline {;~~~~~~~~~~~~~~;}}} =   {displaystyle sec theta } mp {displaystyle csc theta } - {displaystyle sec theta } pm {displaystyle csc theta }   {displaystyle sec theta }
{displaystyle tan {underline {;~~~~~~~~~~~~~~;}}} = - tan theta mp cot theta pm tan theta mp cot theta pm tan theta
{displaystyle cot {underline {;~~~~~~~~~~~~~~;}}} = - cot theta mp tan theta pm cot theta mp tan theta pm cot theta

These formulas imply, in particular, that the following hold:

{displaystyle {begin{alignedat}{28}sin theta &=-&&sin(-theta )&&=-&&sin(pi +theta )&&=&&sin(pi -theta )&&=-&&cos {Big (}{frac {pi }{2}}+theta {Big )}&&=;&&cos {Big (}{frac {pi }{2}}-theta {Big )}&&=-&&cos {Big (}-{frac {pi }{2}}-theta {Big )}&&=&&cos {Big (}-{frac {pi }{2}}+theta {Big )}&&=-&&cos {bigg (}{frac {3pi }{2}}-theta {bigg )}&&=-&&cos {bigg (}-{frac {3pi }{2}}+theta {bigg )}\[0.3ex]cos theta &=&&cos(-theta )&&=-&&cos(pi +theta )&&=&&cos(pi -theta )&&=&&sin {Big (}{frac {pi }{2}}+theta {Big )}&&=&&sin {Big (}{frac {pi }{2}}-theta {Big )}&&=-&&sin {Big (}-{frac {pi }{2}}-theta {Big )}&&=-&&sin {Big (}-{frac {pi }{2}}+theta {Big )}&&=-&&sin {bigg (}{frac {3pi }{2}}-theta {bigg )}&&=&&sin {bigg (}-{frac {3pi }{2}}+theta {bigg )}\[0.3ex]tan theta &=-&&tan(-theta )&&=&&tan(pi +theta )&&=-&&tan(pi -theta )&&=-&&cot {Big (}{frac {pi }{2}}+theta {Big )}&&=&&cot {Big (}{frac {pi }{2}}-theta {Big )}&&=&&cot {Big (}-{frac {pi }{2}}-theta {Big )}&&=-&&cot {Big (}-{frac {pi }{2}}+theta {Big )}&&=&&cot {bigg (}{frac {3pi }{2}}-theta {bigg )}&&=-&&cot {bigg (}-{frac {3pi }{2}}+theta {bigg )}\[0.3ex]end{alignedat}}}

where swapping {displaystyle sin leftrightarrow csc ,} swapping {displaystyle cos leftrightarrow sec ,} and swapping {displaystyle tan leftrightarrow cot } gives the analogous equations for {displaystyle csc ,sec ,{text{ and }}cot ,} respectively.

So for example, by using the equality {textstyle sin left({frac {pi }{2}}-theta right)=cos theta ,} the equation {displaystyle cos theta =x} can be transformed into {textstyle sin left({frac {pi }{2}}-theta right)=x,} which allows for the solution to the equation {displaystyle ;sin varphi =x;} (where {textstyle varphi :={frac {pi }{2}}-theta }) to be used; that solution being:
{displaystyle varphi =(-1)^{k}arcsin(x)+pi k;{text{ for some }}kin mathbb {Z} ,}
which becomes:

{displaystyle {frac {pi }{2}}-theta ~=~(-1)^{k}arcsin(x)+pi kquad {text{ for some }}kin mathbb {Z} }

where using the fact that {displaystyle (-1)^{k}=(-1)^{-k}} and substituting {displaystyle h:=-k} proves that another solution to {displaystyle ;cos theta =x;} is:

{displaystyle theta ~=~(-1)^{h+1}arcsin(x)+pi h+{frac {pi }{2}}quad {text{ for some }}hin mathbb {Z} .}

The substitution {displaystyle ;arcsin x={frac {pi }{2}}-arccos x;} may be used express the right hand side of the above formula in terms of {displaystyle ;arccos x;} instead of {displaystyle ;arcsin x.;}

Equal identical trigonometric functions[edit]

The table below shows how two angles theta and varphi must be related if their values under a given trigonometric function are equal or negatives of each other.

Equation if and only if Solution where… Also a solution to
sin theta = {displaystyle sin varphi } iff {displaystyle theta =} (-1)^{k} varphi + {displaystyle pi k} for some {displaystyle kin mathbb {Z} } {displaystyle csc theta =csc varphi }
cos theta = {displaystyle cos varphi } iff {displaystyle theta =} {displaystyle pm ,} varphi + 2 {displaystyle pi k} for some {displaystyle kin mathbb {Z} } {displaystyle sec theta =sec varphi }
tan theta = {displaystyle tan varphi } iff {displaystyle theta =} varphi + {displaystyle pi k} for some {displaystyle kin mathbb {Z} } {displaystyle cot theta =cot varphi }
{displaystyle -sin theta } = {displaystyle sin varphi } iff {displaystyle theta =} {displaystyle (-1)^{k+1}} varphi + {displaystyle pi k} for some {displaystyle kin mathbb {Z} } {displaystyle -csc theta =csc varphi }
{displaystyle -cos theta } = {displaystyle cos varphi } iff {displaystyle theta =} {displaystyle pm ,} varphi + 2 {displaystyle pi k} {displaystyle +,;pi } for some {displaystyle kin mathbb {Z} } {displaystyle -sec theta =sec varphi }
{displaystyle -tan theta } = {displaystyle tan varphi } iff {displaystyle theta =} - varphi + {displaystyle pi k} for some {displaystyle kin mathbb {Z} } {displaystyle -cot theta =cot varphi }
{displaystyle left|sin theta right|} = {displaystyle left|sin varphi right|} iff {displaystyle theta =} pm varphi + {displaystyle pi k} for some {displaystyle kin mathbb {Z} } {displaystyle {begin{aligned}left|tan theta right|&=left|tan varphi right|\left|csc theta right|&=left|csc varphi right|\left|sec theta right|&=left|sec varphi right|\left|cot theta right|&=left|cot varphi right|end{aligned}}}
⇕
{displaystyle left|cos theta right|} = {displaystyle left|cos varphi right|}

Relationships between trigonometric functions and inverse trigonometric functions[edit]

Trigonometric functions of inverse trigonometric functions are tabulated below. A quick way to derive them is by considering the geometry of a right-angled triangle, with one side of length 1 and another side of length x, then applying the Pythagorean theorem and definitions of the trigonometric ratios. Purely algebraic derivations are longer.[citation needed] It is worth noting that for arcsecant and arccosecant, the diagram assumes that x is positive, and thus the result has to be corrected through the use of absolute values and the signum (sgn) operation.

theta sin(theta ) cos(theta ) tan(theta ) Diagram
arcsin(x) sin(arcsin(x))=x cos(arcsin(x))={sqrt {1-x^{2}}} tan(arcsin(x))={frac {x}{sqrt {1-x^{2}}}} Trigonometric functions and inverse3.svg
arccos(x) sin(arccos(x))={sqrt {1-x^{2}}} cos(arccos(x))=x tan(arccos(x))={frac {sqrt {1-x^{2}}}{x}} Trigonometric functions and inverse.svg
arctan(x) sin(arctan(x))={frac {x}{sqrt {1+x^{2}}}} cos(arctan(x))={frac {1}{sqrt {1+x^{2}}}} tan(arctan(x))=x Trigonometric functions and inverse2.svg
operatorname {arccot}(x) sin(operatorname {arccot}(x))={frac {1}{sqrt {1+x^{2}}}} cos(operatorname {arccot}(x))={frac {x}{sqrt {1+x^{2}}}} tan(operatorname {arccot}(x))={frac {1}{x}} Trigonometric functions and inverse4.svg
operatorname {arcsec}(x) {displaystyle sin(operatorname {arcsec}(x))={frac {sqrt {x^{2}-1}}{|x|}}} cos(operatorname {arcsec}(x))={frac {1}{x}} {displaystyle tan(operatorname {arcsec}(x))=operatorname {sgn}(x){sqrt {x^{2}-1}}} Trigonometric functions and inverse6.svg
operatorname {arccsc}(x) sin(operatorname {arccsc}(x))={frac {1}{x}} {displaystyle cos(operatorname {arccsc}(x))={frac {sqrt {x^{2}-1}}{|x|}}} {displaystyle tan(operatorname {arccsc}(x))={frac {operatorname {sgn}(x)}{sqrt {x^{2}-1}}}} Trigonometric functions and inverse5.svg

Relationships among the inverse trigonometric functions[edit]

The usual principal values of the arcsin(x) (red) and arccos(x) (blue) functions graphed on the cartesian plane.

The usual principal values of the arctan(x) and arccot(x) functions graphed on the cartesian plane.

Principal values of the arcsec(x) and arccsc(x) functions graphed on the cartesian plane.

Complementary angles:

{begin{aligned}arccos(x)&={frac {pi }{2}}-arcsin(x)\[0.5em]operatorname {arccot}(x)&={frac {pi }{2}}-arctan(x)\[0.5em]operatorname {arccsc}(x)&={frac {pi }{2}}-operatorname {arcsec}(x)end{aligned}}

Negative arguments:

{displaystyle {begin{aligned}arcsin(-x)&=-arcsin(x)\arccos(-x)&=pi -arccos(x)\arctan(-x)&=-arctan(x)\operatorname {arccot}(-x)&=pi -operatorname {arccot}(x)\operatorname {arcsec}(-x)&=pi -operatorname {arcsec}(x)\operatorname {arccsc}(-x)&=-operatorname {arccsc}(x)end{aligned}}}

Reciprocal arguments:

{displaystyle {begin{aligned}arccos left({frac {1}{x}}right)&=operatorname {arcsec}(x)\[0.3em]arcsin left({frac {1}{x}}right)&=operatorname {arccsc}(x)\[0.3em]arctan left({frac {1}{x}}right)&={frac {pi }{2}}-arctan(x)=operatorname {arccot}(x),,{text{ if }}x>0\[0.3em]arctan left({frac {1}{x}}right)&=-{frac {pi }{2}}-arctan(x)=operatorname {arccot}(x)-pi ,,{text{ if }}x<0\[0.3em]operatorname {arccot} left({frac {1}{x}}right)&={frac {pi }{2}}-operatorname {arccot}(x)=arctan(x),,{text{ if }}x>0\[0.3em]operatorname {arccot} left({frac {1}{x}}right)&={frac {3pi }{2}}-operatorname {arccot}(x)=pi +arctan(x),,{text{ if }}x<0\[0.3em]operatorname {arcsec} left({frac {1}{x}}right)&=arccos(x)\[0.3em]operatorname {arccsc} left({frac {1}{x}}right)&=arcsin(x)end{aligned}}}

Useful identities if one only has a fragment of a sine table:

{displaystyle {begin{aligned}arccos(x)&=arcsin left({sqrt {1-x^{2}}}right),,{text{ if }}0leq xleq 1{text{ , from which you get }}\arccos &left({frac {1-x^{2}}{1+x^{2}}}right)=arcsin left({frac {2x}{1+x^{2}}}right),,{text{ if }}0leq xleq 1\arcsin &left({sqrt {1-x^{2}}}right)={frac {pi }{2}}-operatorname {sgn}(x)arcsin(x)\arccos(x)&={frac {1}{2}}arccos left(2x^{2}-1right),,{text{ if }}0leq xleq 1\arcsin(x)&={frac {1}{2}}arccos left(1-2x^{2}right),,{text{ if }}0leq xleq 1\arcsin(x)&=arctan left({frac {x}{sqrt {1-x^{2}}}}right)\arccos(x)&=arctan left({frac {sqrt {1-x^{2}}}{x}}right)\arctan(x)&=arcsin left({frac {x}{sqrt {1+x^{2}}}}right)\operatorname {arccot}(x)&=arccos left({frac {x}{sqrt {1+x^{2}}}}right)end{aligned}}}

Whenever the square root of a complex number is used here, we choose the root with the positive real part (or positive imaginary part if the square was negative real).

A useful form that follows directly from the table above is

{displaystyle arctan left(xright)=arccos left({sqrt {frac {1}{1+x^{2}}}}right),,{text{ if }}xgeq 0}.

It is obtained by recognizing that {displaystyle cos left(arctan left(xright)right)={sqrt {frac {1}{1+x^{2}}}}=cos left(arccos left({sqrt {frac {1}{1+x^{2}}}}right)right)}.

From the half-angle formula, {displaystyle tan left({tfrac {theta }{2}}right)={tfrac {sin(theta )}{1+cos(theta )}}}, we get:

{displaystyle {begin{aligned}arcsin(x)&=2arctan left({frac {x}{1+{sqrt {1-x^{2}}}}}right)\[0.5em]arccos(x)&=2arctan left({frac {sqrt {1-x^{2}}}{1+x}}right),,{text{ if }}-1<xleq 1\[0.5em]arctan(x)&=2arctan left({frac {x}{1+{sqrt {1+x^{2}}}}}right)end{aligned}}}

Arctangent addition formula[edit]

{displaystyle arctan(u)pm arctan(v)=arctan left({frac {upm v}{1mp uv}}right){pmod {pi }},,quad uvneq 1,.}

This is derived from the tangent addition formula

{displaystyle tan(alpha pm beta )={frac {tan(alpha )pm tan(beta )}{1mp tan(alpha )tan(beta )}},,}

by letting

alpha =arctan(u),,quad beta =arctan(v),.

In calculus[edit]

Derivatives of inverse trigonometric functions[edit]

The derivatives for complex values of z are as follows:

{displaystyle {begin{aligned}{frac {d}{dz}}arcsin(z)&{}={frac {1}{sqrt {1-z^{2}}}};;&z&{}neq -1,+1\{frac {d}{dz}}arccos(z)&{}=-{frac {1}{sqrt {1-z^{2}}}};;&z&{}neq -1,+1\{frac {d}{dz}}arctan(z)&{}={frac {1}{1+z^{2}}};;&z&{}neq -i,+i\{frac {d}{dz}}operatorname {arccot}(z)&{}=-{frac {1}{1+z^{2}}};;&z&{}neq -i,+i\{frac {d}{dz}}operatorname {arcsec}(z)&{}={frac {1}{z^{2}{sqrt {1-{frac {1}{z^{2}}}}}}};;&z&{}neq -1,0,+1\{frac {d}{dz}}operatorname {arccsc}(z)&{}=-{frac {1}{z^{2}{sqrt {1-{frac {1}{z^{2}}}}}}};;&z&{}neq -1,0,+1end{aligned}}}

Only for real values of x:

{displaystyle {begin{aligned}{frac {d}{dx}}operatorname {arcsec}(x)&{}={frac {1}{|x|{sqrt {x^{2}-1}}}};;&|x|>1\{frac {d}{dx}}operatorname {arccsc}(x)&{}=-{frac {1}{|x|{sqrt {x^{2}-1}}}};;&|x|>1end{aligned}}}

For a sample derivation: if {displaystyle theta =arcsin(x)}, we get:

{displaystyle {frac {darcsin(x)}{dx}}={frac {dtheta }{dsin(theta )}}={frac {dtheta }{cos(theta ),dtheta }}={frac {1}{cos(theta )}}={frac {1}{sqrt {1-sin ^{2}(theta )}}}={frac {1}{sqrt {1-x^{2}}}}}

Expression as definite integrals[edit]

Integrating the derivative and fixing the value at one point gives an expression for the inverse trigonometric function as a definite integral:

{displaystyle {begin{aligned}arcsin(x)&{}=int _{0}^{x}{frac {1}{sqrt {1-z^{2}}}},dz;,&|x|&{}leq 1\arccos(x)&{}=int _{x}^{1}{frac {1}{sqrt {1-z^{2}}}},dz;,&|x|&{}leq 1\arctan(x)&{}=int _{0}^{x}{frac {1}{z^{2}+1}},dz;,\operatorname {arccot}(x)&{}=int _{x}^{infty }{frac {1}{z^{2}+1}},dz;,\operatorname {arcsec}(x)&{}=int _{1}^{x}{frac {1}{z{sqrt {z^{2}-1}}}},dz=pi +int _{-x}^{-1}{frac {1}{z{sqrt {z^{2}-1}}}},dz;,&x&{}geq 1\operatorname {arccsc}(x)&{}=int _{x}^{infty }{frac {1}{z{sqrt {z^{2}-1}}}},dz=int _{-infty }^{-x}{frac {1}{z{sqrt {z^{2}-1}}}},dz;,&x&{}geq 1\end{aligned}}}

When x equals 1, the integrals with limited domains are improper integrals, but still well-defined.

Infinite series[edit]

Similar to the sine and cosine functions, the inverse trigonometric functions can also be calculated using power series, as follows. For arcsine, the series can be derived by expanding its derivative, {textstyle {tfrac {1}{sqrt {1-z^{2}}}}}, as a binomial series, and integrating term by term (using the integral definition as above). The series for arctangent can similarly be derived by expanding its derivative {textstyle {frac {1}{1+z^{2}}}} in a geometric series, and applying the integral definition above (see Leibniz series).

{displaystyle {begin{aligned}arcsin(z)&=z+left({frac {1}{2}}right){frac {z^{3}}{3}}+left({frac {1cdot 3}{2cdot 4}}right){frac {z^{5}}{5}}+left({frac {1cdot 3cdot 5}{2cdot 4cdot 6}}right){frac {z^{7}}{7}}+cdots \[5pt]&=sum _{n=0}^{infty }{frac {(2n-1)!!}{(2n)!!}}{frac {z^{2n+1}}{2n+1}}\[5pt]&=sum _{n=0}^{infty }{frac {(2n)!}{(2^{n}n!)^{2}}}{frac {z^{2n+1}}{2n+1}},;qquad |z|leq 1end{aligned}}}
{displaystyle arctan(z)=z-{frac {z^{3}}{3}}+{frac {z^{5}}{5}}-{frac {z^{7}}{7}}+cdots =sum _{n=0}^{infty }{frac {(-1)^{n}z^{2n+1}}{2n+1}},;qquad |z|leq 1qquad zneq i,-i}

Series for the other inverse trigonometric functions can be given in terms of these according to the relationships given above. For example, {displaystyle arccos(x)=pi /2-arcsin(x)}, {displaystyle operatorname {arccsc}(x)=arcsin(1/x)}, and so on. Another series is given by:[19]

{displaystyle 2left(arcsin left({frac {x}{2}}right)right)^{2}=sum _{n=1}^{infty }{frac {x^{2n}}{n^{2}{binom {2n}{n}}}}.}

Leonhard Euler found a series for the arctangent that converges more quickly than its Taylor series:

{displaystyle arctan(z)={frac {z}{1+z^{2}}}sum _{n=0}^{infty }prod _{k=1}^{n}{frac {2kz^{2}}{(2k+1)(1+z^{2})}}.}[20]

(The term in the sum for n = 0 is the empty product, so is 1.)

Alternatively, this can be expressed as

{displaystyle arctan(z)=sum _{n=0}^{infty }{frac {2^{2n}(n!)^{2}}{(2n+1)!}}{frac {z^{2n+1}}{(1+z^{2})^{n+1}}}.}

Another series for the arctangent function is given by

{displaystyle arctan(z)=isum _{n=1}^{infty }{frac {1}{2n-1}}left({frac {1}{(1+2i/z)^{2n-1}}}-{frac {1}{(1-2i/z)^{2n-1}}}right),}

where i=sqrt{-1} is the imaginary unit.[21]

Continued fractions for arctangent[edit]

Two alternatives to the power series for arctangent are these generalized continued fractions:

{displaystyle arctan(z)={frac {z}{1+{cfrac {(1z)^{2}}{3-1z^{2}+{cfrac {(3z)^{2}}{5-3z^{2}+{cfrac {(5z)^{2}}{7-5z^{2}+{cfrac {(7z)^{2}}{9-7z^{2}+ddots }}}}}}}}}}={frac {z}{1+{cfrac {(1z)^{2}}{3+{cfrac {(2z)^{2}}{5+{cfrac {(3z)^{2}}{7+{cfrac {(4z)^{2}}{9+ddots }}}}}}}}}}}

The second of these is valid in the cut complex plane. There are two cuts, from −i to the point at infinity, going down the imaginary axis, and from i to the point at infinity, going up the same axis. It works best for real numbers running from −1 to 1. The partial denominators are the odd natural numbers, and the partial numerators (after the first) are just (nz)2, with each perfect square appearing once. The first was developed by Leonhard Euler; the second by Carl Friedrich Gauss utilizing the Gaussian hypergeometric series.

Indefinite integrals of inverse trigonometric functions[edit]

For real and complex values of z:

{displaystyle {begin{aligned}int arcsin(z),dz&{}=z,arcsin(z)+{sqrt {1-z^{2}}}+C\int arccos(z),dz&{}=z,arccos(z)-{sqrt {1-z^{2}}}+C\int arctan(z),dz&{}=z,arctan(z)-{frac {1}{2}}ln left(1+z^{2}right)+C\int operatorname {arccot}(z),dz&{}=z,operatorname {arccot}(z)+{frac {1}{2}}ln left(1+z^{2}right)+C\int operatorname {arcsec}(z),dz&{}=z,operatorname {arcsec}(z)-ln left[zleft(1+{sqrt {frac {z^{2}-1}{z^{2}}}}right)right]+C\int operatorname {arccsc}(z),dz&{}=z,operatorname {arccsc}(z)+ln left[zleft(1+{sqrt {frac {z^{2}-1}{z^{2}}}}right)right]+Cend{aligned}}}

For real x ≥ 1:

{displaystyle {begin{aligned}int operatorname {arcsec}(x),dx&{}=x,operatorname {arcsec}(x)-ln left(x+{sqrt {x^{2}-1}}right)+C\int operatorname {arccsc}(x),dx&{}=x,operatorname {arccsc}(x)+ln left(x+{sqrt {x^{2}-1}}right)+Cend{aligned}}}

For all real x not between -1 and 1:

{displaystyle {begin{aligned}int operatorname {arcsec}(x),dx&{}=x,operatorname {arcsec}(x)-operatorname {sgn}(x)ln left|x+{sqrt {x^{2}-1}}right|+C\int operatorname {arccsc}(x),dx&{}=x,operatorname {arccsc}(x)+operatorname {sgn}(x)ln left|x+{sqrt {x^{2}-1}}right|+Cend{aligned}}}

The absolute value is necessary to compensate for both negative and positive values of the arcsecant and arccosecant functions. The signum function is also necessary due to the absolute values in the derivatives of the two functions, which create two different solutions for positive and negative values of x. These can be further simplified using the logarithmic definitions of the inverse hyperbolic functions:

{displaystyle {begin{aligned}int operatorname {arcsec}(x),dx&{}=x,operatorname {arcsec}(x)-operatorname {arcosh} (|x|)+C\int operatorname {arccsc}(x),dx&{}=x,operatorname {arccsc}(x)+operatorname {arcosh} (|x|)+C\end{aligned}}}

The absolute value in the argument of the arcosh function creates a negative half of its graph, making it identical to the signum logarithmic function shown above.

All of these antiderivatives can be derived using integration by parts and the simple derivative forms shown above.

Example[edit]

Using {displaystyle int u,dv=uv-int v,du} (i.e. integration by parts), set

{displaystyle {begin{aligned}u&=arcsin(x)&dv&=dx\du&={frac {dx}{sqrt {1-x^{2}}}}&v&=xend{aligned}}}

Then

{displaystyle int arcsin(x),dx=xarcsin(x)-int {frac {x}{sqrt {1-x^{2}}}},dx,}

which by the simple substitution {displaystyle w=1-x^{2}, dw=-2x,dx} yields the final result:

{displaystyle int arcsin(x),dx=xarcsin(x)+{sqrt {1-x^{2}}}+C}

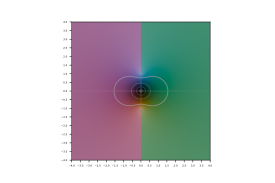
Extension to complex plane[edit]

A Riemann surface for the argument of the relation tan z = x. The orange sheet in the middle is the principal sheet representing arctan x. The blue sheet above and green sheet below are displaced by 2π and −2π respectively.

Since the inverse trigonometric functions are analytic functions, they can be extended from the real line to the complex plane. This results in functions with multiple sheets and branch points. One possible way of defining the extension is:

{displaystyle arctan(z)=int _{0}^{z}{frac {dx}{1+x^{2}}}quad zneq -i,+i}

where the part of the imaginary axis which does not lie strictly between the branch points (−i and +i) is the branch cut between the principal sheet and other sheets. The path of the integral must not cross a branch cut. For z not on a branch cut, a straight line path from 0 to z is such a path. For z on a branch cut, the path must approach from Re[x] > 0 for the upper branch cut and from Re[x] < 0 for the lower branch cut.

The arcsine function may then be defined as:

{displaystyle arcsin(z)=arctan left({frac {z}{sqrt {1-z^{2}}}}right)quad zneq -1,+1}

where (the square-root function has its cut along the negative real axis and) the part of the real axis which does not lie strictly between −1 and +1 is the branch cut between the principal sheet of arcsin and other sheets;

{displaystyle arccos(z)={frac {pi }{2}}-arcsin(z)quad zneq -1,+1}

which has the same cut as arcsin;

{displaystyle operatorname {arccot}(z)={frac {pi }{2}}-arctan(z)quad zneq -i,i}

which has the same cut as arctan;

{displaystyle operatorname {arcsec}(z)=arccos left({frac {1}{z}}right)quad zneq -1,0,+1}

where the part of the real axis between −1 and +1 inclusive is the cut between the principal sheet of arcsec and other sheets;

{displaystyle operatorname {arccsc}(z)=arcsin left({frac {1}{z}}right)quad zneq -1,0,+1}

which has the same cut as arcsec.

Logarithmic forms[edit]

These functions may also be expressed using complex logarithms. This extends their domains to the complex plane in a natural fashion. The following identities for principal values of the functions hold everywhere that they are defined, even on their branch cuts.

{displaystyle {begin{aligned}arcsin(z)&{}=-iln left({sqrt {1-z^{2}}}+izright)=iln left({sqrt {1-z^{2}}}-izright)&{}=operatorname {arccsc} left({frac {1}{z}}right)\[10pt]arccos(z)&{}=-iln left(i{sqrt {1-z^{2}}}+zright)={frac {pi }{2}}-arcsin(z)&{}=operatorname {arcsec} left({frac {1}{z}}right)\[10pt]arctan(z)&{}=-{frac {i}{2}}ln left({frac {i-z}{i+z}}right)=-{frac {i}{2}}ln left({frac {1+iz}{1-iz}}right)&{}=operatorname {arccot} left({frac {1}{z}}right)\[10pt]operatorname {arccot}(z)&{}=-{frac {i}{2}}ln left({frac {z+i}{z-i}}right)=-{frac {i}{2}}ln left({frac {iz-1}{iz+1}}right)&{}=arctan left({frac {1}{z}}right)\[10pt]operatorname {arcsec}(z)&{}=-iln left(i{sqrt {1-{frac {1}{z^{2}}}}}+{frac {1}{z}}right)={frac {pi }{2}}-operatorname {arccsc}(z)&{}=arccos left({frac {1}{z}}right)\[10pt]operatorname {arccsc}(z)&{}=-iln left({sqrt {1-{frac {1}{z^{2}}}}}+{frac {i}{z}}right)=iln left({sqrt {1-{frac {1}{z^{2}}}}}-{frac {i}{z}}right)&{}=arcsin left({frac {1}{z}}right)end{aligned}}}

Generalization[edit]

Because all of the inverse trigonometric functions output an angle of a right triangle, they can be generalized by using Euler’s formula to form a right triangle in the complex plane. Algebraically, this gives us:

{displaystyle ce^{itheta }=ccos(theta )+icsin(theta )}

or

{displaystyle ce^{itheta }=a+ib}

where a is the adjacent side, b is the opposite side, and c is the hypotenuse. From here, we can solve for theta .

{displaystyle {begin{aligned}e^{ln(c)+itheta }&=a+ib\ln c+itheta &=ln(a+ib)\theta &=operatorname {Im} left(ln(a+ib)right)end{aligned}}}

or

{displaystyle theta =-iln left({frac {a+ib}{c}}right)}

Simply taking the imaginary part works for any real-valued a and b, but if a or b is complex-valued, we have to use the final equation so that the real part of the result isn’t excluded. Since the length of the hypotenuse doesn’t change the angle, ignoring the real part of {displaystyle ln(a+bi)} also removes c from the equation. In the final equation, we see that the angle of the triangle in the complex plane can be found by inputting the lengths of each side. By setting one of the three sides equal to 1 and one of the remaining sides equal to our input z, we obtain a formula for one of the inverse trig functions, for a total of six equations. Because the inverse trig functions require only one input, we must put the final side of the triangle in terms of the other two using the Pythagorean Theorem relation

{displaystyle a^{2}+b^{2}=c^{2}}

The table below shows the values of a, b, and c for each of the inverse trig functions and the equivalent expressions for theta that result from plugging the values into the equations above and simplifying.

{displaystyle {begin{aligned}&a&&b&&c&&-iln left({frac {a+ib}{c}}right)&&theta &&theta _{a,bin mathbb {R} }\arcsin(z) &{sqrt {1-z^{2}}}&&z&&1&&-iln left({frac {{sqrt {1-z^{2}}}+iz}{1}}right)&&=-iln left({sqrt {1-z^{2}}}+izright)&&operatorname {Im} left(ln left({sqrt {1-z^{2}}}+izright)right)\arccos(z) &z&&{sqrt {1-z^{2}}}&&1&&-iln left({frac {z+i{sqrt {1-z^{2}}}}{1}}right)&&=-iln left(z+{sqrt {z^{2}-1}}right)&&operatorname {Im} left(ln left(z+{sqrt {z^{2}-1}}right)right)\arctan(z) &1&&z&&{sqrt {1+z^{2}}}&&-iln left({frac {1+iz}{sqrt {1+z^{2}}}}right)&&=-iln left({frac {1+iz}{sqrt {1+z^{2}}}}right)&&operatorname {Im} left(ln left(1+izright)right)\operatorname {arccot}(z) &z&&1&&{sqrt {z^{2}+1}}&&-iln left({frac {z+i}{sqrt {z^{2}+1}}}right)&&=-iln left({frac {z+i}{sqrt {z^{2}+1}}}right)&&operatorname {Im} left(ln left(z+iright)right)\operatorname {arcsec}(z) &1&&{sqrt {z^{2}-1}}&&z&&-iln left({frac {1+i{sqrt {z^{2}-1}}}{z}}right)&&=-iln left({frac {1}{z}}+{sqrt {{frac {1}{z^{2}}}-1}}right)&&operatorname {Im} left(ln left({frac {1}{z}}+{sqrt {{frac {1}{z^{2}}}-1}}right)right)\operatorname {arccsc}(z) &{sqrt {z^{2}-1}}&&1&&z&&-iln left({frac {{sqrt {z^{2}-1}}+i}{z}}right)&&=-iln left({sqrt {1-{frac {1}{z^{2}}}}}+{frac {i}{z}}right)&&operatorname {Im} left(ln left({sqrt {1-{frac {1}{z^{2}}}}}+{frac {i}{z}}right)right)\end{aligned}}}

In order to match the principal branch of the natural log and square root functions to the usual principal branch of the inverse trig functions, the particular form of the simplified formulation matters. The formulations given in the two rightmost columns assume {displaystyle operatorname {Im} left(ln zright)in (-pi ,pi ]} and {displaystyle operatorname {Re} left({sqrt {z}}right)geq 0}. To match the principal branch {displaystyle operatorname {Im} left(ln zright)in [0,2pi )} and {displaystyle operatorname {Im} left({sqrt {z}}right)geq 0} to the usual principal branch of the inverse trig functions, subtract 2pi from the result theta when {displaystyle operatorname {Re} (theta )>pi }.

In this sense, all of the inverse trig functions can be thought of as specific cases of the complex-valued log function. Since these definition work for any complex-valued z, the definitions allow for hyperbolic angles as outputs and can be used to further define the inverse hyperbolic functions. Elementary proofs of the relations may also proceed via expansion to exponential forms of the trigonometric functions.

Example proof[edit]

{displaystyle {begin{aligned}sin(phi )&=z\phi &=arcsin(z)end{aligned}}}

Using the exponential definition of sine, and letting {displaystyle xi =e^{iphi },}

{displaystyle {begin{aligned}z&={frac {e^{iphi }-e^{-iphi }}{2i}}\[10mu]2iz&=xi -{frac {1}{xi }}\[5mu]0&=xi ^{2}-2izxi -1\[5mu]xi &=izpm {sqrt {1-z^{2}}}\[5mu]phi &=-iln left(izpm {sqrt {1-z^{2}}}right)end{aligned}}}

(the positive branch is chosen)

phi =arcsin(z)=-iln left(iz+{sqrt {1-z^{2}}}right)
Color wheel graphs of inverse trigonometric functions in the complex plane

Arcsine of z in the complex plane. Arccosine of z in the complex plane. Arctangent of z in the complex plane.
arcsin(z) arccos(z) arctan(z)
Arccosecant of z in the complex plane. Arcsecant of z in the complex plane. Arccotangent of z in the complex plane.
operatorname {arccsc}(z) operatorname {arcsec}(z) operatorname {arccot}(z)

Applications[edit]

Finding the angle of a right triangle[edit]

Inverse trigonometric functions are useful when trying to determine the remaining two angles of a right triangle when the lengths of the sides of the triangle are known. Recalling the right-triangle definitions of sine and cosine, it follows that

{displaystyle theta =arcsin left({frac {text{opposite}}{text{hypotenuse}}}right)=arccos left({frac {text{adjacent}}{text{hypotenuse}}}right).}

Often, the hypotenuse is unknown and would need to be calculated before using arcsine or arccosine using the Pythagorean Theorem: a^{2}+b^{2}=h^{2} where h is the length of the hypotenuse. Arctangent comes in handy in this situation, as the length of the hypotenuse is not needed.

theta =arctan left({frac {text{opposite}}{text{adjacent}}}right),.

For example, suppose a roof drops 8 feet as it runs out 20 feet. The roof makes an angle θ with the horizontal, where θ may be computed as follows:

theta =arctan left({frac {text{opposite}}{text{adjacent}}}right)=arctan left({frac {text{rise}}{text{run}}}right)=arctan left({frac {8}{20}}right)approx 21.8^{circ },.

In computer science and engineering[edit]

Two-argument variant of arctangent[edit]

The two-argument atan2 function computes the arctangent of y / x given y and x, but with a range of (−π, π]. In other words, atan2(y, x) is the angle between the positive x-axis of a plane and the point (x, y) on it, with positive sign for counter-clockwise angles (upper half-plane, y > 0), and negative sign for clockwise angles (lower half-plane, y < 0). It was first introduced in many computer programming languages, but it is now also common in other fields of science and engineering.

In terms of the standard arctan function, that is with range of (−π/2, π/2), it can be expressed as follows:

{displaystyle operatorname {atan2} (y,x)={begin{cases}arctan left({frac {y}{x}}right)&quad x>0\arctan left({frac {y}{x}}right)+pi &quad ygeq 0,;x<0\arctan left({frac {y}{x}}right)-pi &quad y<0,;x<0\{frac {pi }{2}}&quad y>0,;x=0\-{frac {pi }{2}}&quad y<0,;x=0\{text{undefined}}&quad y=0,;x=0end{cases}}}

It also equals the principal value of the argument of the complex number x + iy.

This limited version of the function above may also be defined using the tangent half-angle formulae as follows:

operatorname {atan2} (y,x)=2arctan left({frac {y}{{sqrt {x^{2}+y^{2}}}+x}}right)

provided that either x > 0 or y ≠ 0. However this fails if given x ≤ 0 and y = 0 so the expression is unsuitable for computational use.

The above argument order (y, x) seems to be the most common, and in particular is used in ISO standards such as the C programming language, but a few authors may use the opposite convention (x, y) so some caution is warranted. These variations are detailed at atan2.

Arctangent function with location parameter[edit]

In many applications[22] the solution y of the equation {displaystyle x=tan(y)} is to come as close as possible to a given value -infty <eta <infty . The adequate solution is produced by the parameter modified arctangent function

{displaystyle y=arctan _{eta }(x):=arctan(x)+pi ,operatorname {rni} left({frac {eta -arctan(x)}{pi }}right),.}

The function operatorname {rni} rounds to the nearest integer.

Numerical accuracy[edit]

For angles near 0 and π, arccosine is ill-conditioned, and similarly with arcsine for angles near −π/2 and π/2. Computer applications thus need to consider the stability of inputs to these functions and the sensitivity of their calculations, or use alternate methods.[23]

See also[edit]

  • Arcsine distribution
  • Inverse exsecant
  • Inverse versine
  • Inverse hyperbolic functions
  • List of integrals of inverse trigonometric functions
  • List of trigonometric identities
  • Trigonometric function
  • Trigonometric functions of matrices

Notes[edit]

  1. ^ To clarify, suppose that it is written «LHS {displaystyle ,iff ,} RHS» where LHS (which abbreviates left hand side) and RHS are both statements that can individually be either be true or false. For example, if theta and s are some given and fixed numbers and if the following is written:

    {displaystyle tan theta =s,iff ,theta =arctan(s)+pi kquad {text{ for some }}kin mathbb {Z} }

    then LHS is the statement «{displaystyle tan theta =s}«. Depending on what specific values theta and s have, this LHS statement can either be true or false. For instance, LHS is true if theta =0 and s=0 (because in this case {displaystyle tan theta =tan 0=s}) but LHS is false if theta =0 and {displaystyle s=2} (because in this case {displaystyle tan theta =tan 0=s} which is not equal to {displaystyle s=2}); more generally, LHS is false if theta =0 and {displaystyle sneq 0.} Similarly, RHS is the statement «{displaystyle theta =arctan(s)+pi k} for some {displaystyle kin mathbb {Z} }«. The RHS statement can also either true or false (as before, whether the RHS statement is true or false depends on what specific values theta and s have). The logical equality symbol {displaystyle ,iff ,} means that (a) if the LHS statement is true then the RHS statement is also necessarily true, and moreover (b) if the LHS statement is false then the RHS statement is also necessarily false. Similarly, {displaystyle ,iff ,} also means that (c) if the RHS statement is true then the LHS statement is also necessarily true, and moreover (d) if the RHS statement is false then the LHS statement is also necessarily false.

References[edit]

  • Abramowitz, Milton; Stegun, Irene A., eds. (1972). Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. New York: Dover Publications. ISBN 978-0-486-61272-0.
  1. ^ Taczanowski, Stefan (1 October 1978). «On the optimization of some geometric parameters in 14 MeV neutron activation analysis». Nuclear Instruments and Methods. ScienceDirect. 155 (3): 543–546. Bibcode:1978NucIM.155..543T. doi:10.1016/0029-554X(78)90541-4.
  2. ^ Hazewinkel, Michiel (1994) [1987]. Encyclopaedia of Mathematics (unabridged reprint ed.). Kluwer Academic Publishers / Springer Science & Business Media. ISBN 978-155608010-4.
  3. ^ Ebner, Dieter (25 July 2005). Preparatory Course in Mathematics (PDF) (6 ed.). Department of Physics, University of Konstanz. Archived (PDF) from the original on 26 July 2017. Retrieved 26 July 2017.
  4. ^ Mejlbro, Leif (11 November 2010). Stability, Riemann Surfaces, Conformal Mappings — Complex Functions Theory (PDF) (1 ed.). Ventus Publishing ApS / Bookboon. ISBN 978-87-7681-702-2. Archived from the original (PDF) on 26 July 2017. Retrieved 26 July 2017.
  5. ^ Durán, Mario (2012). Mathematical methods for wave propagation in science and engineering. Vol. 1: Fundamentals (1 ed.). Ediciones UC. p. 88. ISBN 978-956141314-6.
  6. ^ a b c d Hall, Arthur Graham; Frink, Fred Goodrich (January 1909). «Chapter II. The Acute Angle [14] Inverse trigonometric functions». Written at Ann Arbor, Michigan, USA. Trigonometry. Vol. Part I: Plane Trigonometry. New York, USA: Henry Holt and Company / Norwood Press / J. S. Cushing Co. — Berwick & Smith Co., Norwood, Massachusetts, USA. p. 15. Retrieved 12 August 2017. […] α = arcsin m: It is frequently read «arc-sine m» or «anti-sine m,» since two mutually inverse functions are said each to be the anti-function of the other. […] A similar symbolic relation holds for the other trigonometric functions. […] This notation is universally used in Europe and is fast gaining ground in this country. A less desirable symbol, α = sin-1m, is still found in English and American texts. The notation α = inv sin m is perhaps better still on account of its general applicability. […]
  7. ^ Klein, Christian Felix (1924) [1902]. Elementarmathematik vom höheren Standpunkt aus: Arithmetik, Algebra, Analysis (in German). Vol. 1 (3rd ed.). Berlin: J. Springer.
  8. ^ Klein, Christian Felix (2004) [1932]. Elementary Mathematics from an Advanced Standpoint: Arithmetic, Algebra, Analysis. Translated by Hedrick, E. R.; Noble, C. A. (Translation of 3rd German ed.). Dover Publications, Inc. / The Macmillan Company. ISBN 978-0-48643480-3. Retrieved 13 August 2017.
  9. ^ Dörrie, Heinrich (1965). Triumph der Mathematik. Translated by Antin, David. Dover Publications. p. 69. ISBN 978-0-486-61348-2.
  10. ^ Weisstein, Eric W. «Inverse Trigonometric Functions». mathworld.wolfram.com. Retrieved 29 August 2020.
  11. ^ Beach, Frederick Converse; Rines, George Edwin, eds. (1912). «Inverse trigonometric functions». The Americana: a universal reference library. Vol. 21.
  12. ^ Cook, John D. (11 February 2021). «Trig functions across programming languages». johndcook.com (blog). Retrieved 10 March 2021.
  13. ^ Cajori, Florian (1919). A History of Mathematics (2 ed.). New York, NY: The Macmillan Company. p. 272.
  14. ^ Herschel, John Frederick William (1813). «On a remarkable Application of Cotes’s Theorem». Philosophical Transactions. Royal Society, London. 103 (1): 8. doi:10.1098/rstl.1813.0005.
  15. ^ «Inverse trigonometric functions». Wiki. Brilliant Math & Science (brilliant.org). Retrieved 29 August 2020.
  16. ^ Korn, Grandino Arthur; Korn, Theresa M. (2000) [1961]. «21.2.-4. Inverse Trigonometric Functions». Mathematical handbook for scientists and engineers: Definitions, theorems, and formulars for reference and review (3 ed.). Mineola, New York, USA: Dover Publications, Inc. p. 811. ISBN 978-0-486-41147-7.
  17. ^ Bhatti, Sanaullah; Nawab-ud-Din; Ahmed, Bashir; Yousuf, S. M.; Taheem, Allah Bukhsh (1999). «Differentiation of Trigonometric, Logarithmic and Exponential Functions». In Ellahi, Mohammad Maqbool; Dar, Karamat Hussain; Hussain, Faheem (eds.). Calculus and Analytic Geometry (1 ed.). Lahore: Punjab Textbook Board. p. 140.
  18. ^ Abramowitz & Stegun 1972, p. 73, 4.3.44
  19. ^ Borwein, Jonathan; Bailey, David; Gingersohn, Roland (2004). Experimentation in Mathematics: Computational Paths to Discovery (1 ed.). Wellesley, MA, USA: A. K. Peters. p. 51. ISBN 978-1-56881-136-9.
  20. ^ Hwang Chien-Lih (2005), «An elementary derivation of Euler’s series for the arctangent function», The Mathematical Gazette, 89 (516): 469–470, doi:10.1017/S0025557200178404, S2CID 123395287
  21. ^ S. M. Abrarov and B. M. Quine (2018), «A formula for pi involving nested radicals», The Ramanujan Journal, 46 (3): 657–665, arXiv:1610.07713, doi:10.1007/s11139-018-9996-8, S2CID 119150623
  22. ^ when a time varying angle crossing {displaystyle pm pi /2} should be mapped by a smooth line instead of a saw toothed one (robotics, astromomy, angular movement in general)[citation needed]
  23. ^ Gade, Kenneth (2010). «A non-singular horizontal position representation» (PDF). The Journal of Navigation. Cambridge University Press. 63 (3): 395–417. Bibcode:2010JNav…63..395G. doi:10.1017/S0373463309990415.

External links[edit]

  • Weisstein, Eric W. «Inverse Tangent». MathWorld.
Источник

Понравилась статья? Поделить с друзьями:

Не пропустите также:

  • Green hell как найти карту
  • Не поднимается хлеб в хлебопечке как исправить
  • Как составить акт в чрезвычайным ситуациям
  • Дота 2 как найти сборки
  • Как составить звуковую схему слова ели

    • 0 0 голоса
    Рейтинг статьи
    Подписаться
    Уведомить о
    guest

    0 комментариев
    Старые
    Новые Популярные
    Межтекстовые Отзывы
    Посмотреть все комментарии