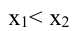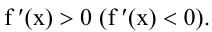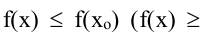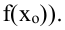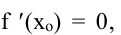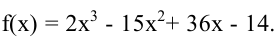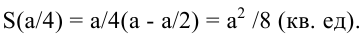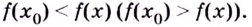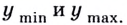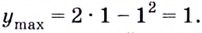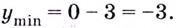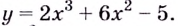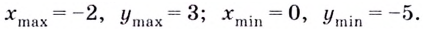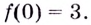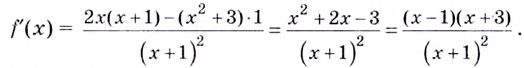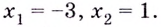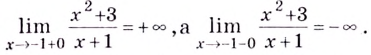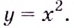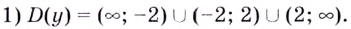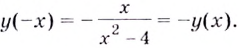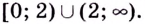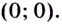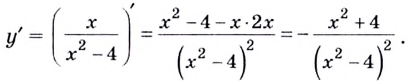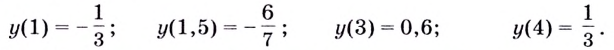Алгебра и начала математического анализа, 11 класс
Урок № 16. Экстремумы функции.
Перечень вопросов, рассматриваемых в теме
1) Определение точек максимума и минимума функции
2) Определение точки экстремума функции
3) Условия достаточные для нахождения точек экстремума функции
Глоссарий по теме
Возрастание функции. Функция y=f(x) возрастает на интервале X, если для любых х1 и х2, 
из этого промежутка выполняется неравенство 
. Другими словами – большему значению аргумента соответствует большее значение функции.
Максимум функции. Значение функции в точке максимума называют максимумом функции
Минимум функции. Значение функции в точке минимума называют минимумом функции
Производная (функции в точке) — основное понятие дифференциального исчисления, которое характеризует скорость изменения функции (в конкретной точке).
Точка максимума функции. Точку х0 называют точкой максимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
.
Точка минимума функции. Точку х0 называют точкой минимума функции y = f(x), если для всех x из ее окрестности справедливо неравенство 
.
Точки экстремума функции. Точки минимума и максимума называют точками экстремума.
Убывание функции. Функция y = f(x) убывает на интервале X, если для любых х1 и х2, 
из этого промежутка выполняется неравенство 
. Другими словами – большему значению аргумента соответствует большее значение функции.
Алгоритм исследования функции на монотонность и экстремумы:
1) Найти область определения функции D(f)
2) Найти f’ (x).
3) Найти стационарные (f'(x) = 0) и критические (f'(x) не
существует) точки функции y = f(x).
4) Отметить стационарные и критические точки на числовой
прямой и определить знаки производной на получившихся
промежутках.
5) Сделать выводы о монотонности функции и точках ее
экстремума.
Основная литература:
Колягин Ю.М., Ткачева М.В, Федорова Н.Е. и др., под ред. Жижченко А.Б. Алгебра и начала математического анализа (базовый и профильный уровни) 11 кл. – М.: Просвещение, 2014.
Дополнительная литература:
Орлова Е. А., Севрюков П. Ф., Сидельников В. И., Смоляков А.Н. Тренировочные тестовые задания по алгебре и началам анализа для учащихся 10-х и 11-х классов: учебное пособие – М.: Илекса; Ставрополь: Сервисшкола, 2011.
Теоретический материал для самостоятельного изучения
Точки, в которых происходит изменение характера монотонности функции – это ТОЧКИ ЭКСТРЕМУМА.
- Точку х = х0 называют точкой минимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≥ f(x0).
- Точку х = х0 называют точкой максимума функции у = f(х), если у этой точки существует окрестность, для всех точек которой выполняется неравенство f(x) ≤ f(x0).
Точки максимума и минимума – точки экстремума.
Функция может иметь неограниченное количество экстремумов.
Критическая точка – это точка, производная в которой равна 0 или не существует.
Важно помнить, что любая точка экстремума является критической точкой, но не всякая критическая является экстремальной.
Алгоритм нахождения максимума/минимума функции на отрезке:
- найти экстремальные точки функции, принадлежащие отрезку,
- найти значение функции в экстремальных точках из пункта 1 и в концах отрезка,
- выбрать из полученных значений максимальное и минимальное.
Примеры и разбор решения заданий тренировочного модуля
№1. Определите промежуток монотонности функции у=х2 -8х +5
Решение: Найдем производную заданной функции: у’=2x-8
2x-8=0
х=4
Определяем знак производной функции и изобразим на рисунке, следовательно, функция возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
Ответ: возрастает при хϵ (4;+∞); убывает при хϵ (-∞;4)
№2. Найдите точку минимума функции у= 2х-ln(х+3)+9
Решение: Найдем производную заданной функции: 
Найдем нули производной: 
х=-2,5
Определим знаки производной функции и изобразим на рисунке поведение функции:
Ответ: -2,5 точка min
№3. Материальная точка движется прямолинейно по закону x(t) = 10t2 − 48t + 15, где x — расстояние от точки отсчета в метрах, t — время в секундах, измеренное с начала движения. Найдите ее скорость (в метрах в секунду) в момент времени t = 3с.
Решение: Если нас интересует движение автомобиля, то, принимая в качестве функции зависимость пройденного расстояния от времени, с помощью производной мы получим зависимость скорости от времени.
V=х'(t)= 20t – 48. Подставляем вместо t 3c и получаем ответ. V=12 мc
Ответ: V=12 мc
№4. На рисунке изображен график функции. На оси абсцисс отмечены семь точек: x1, x2, x3, x4, x5, x6, x7. Определите количество целых точек, в которых производная функции отрицательна.
Решение: Производная функции отрицательна на тех интервалах, на которых функция убывает. В данном случае это точки х3,х5,х7. Следовательно, таких точек 3
Ответ: 3
Содержание:
Экстремум функции
Функция y=f(x) называется возрастающей (убывающей) в некотором интервале, если при 
Если дифференцируемая функция у = f(x) на отрезке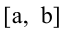 
возрастает (убывает), то ее производная на этом отрезке 
Точка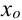 
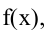
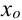
называется точкой локального максимума (минимума) функции 
если существует окрестность точки для всех точек которой верно неравенство 
Точки максимума и минимума называются точками экстремума, а значения функции в этих точках — ее экстремумами.
Необходимые условия экстремума. Если точка хо является точкой экстремума функции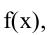 
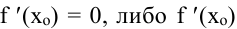
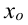
то либо 
не существует. Такие точки называют критическими, причем сама функция в критической точке определена. Экстремумы функции следует искать среди ее критических точек. Первое достаточное условие. Пусть 
— критическая точка. Если f'(х) при переходе через точку 
меняет знак плюс на минус, то в точке функция имеет максимум, в противном случае — минимум. Если при переходе через критическую точку производная не меняет знак, то в точке хо экстремума нет.
Второе достаточное условие. Пусть функция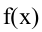 
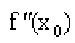
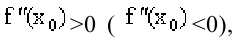
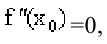
имеет производную f'(х) в окрестности точки и вторую производную 
в самой точке . Если 
то точка является точкой локального минимума (максимума) функции f(x). Если же 
то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные.
На отрезке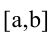 
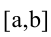
функция у = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка 
.
Пример:
Найти экстремумы функции 
Решение:
Так как 
то критические точки функции 
и 
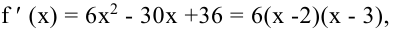
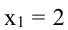
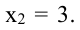
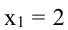
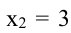
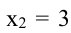
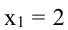
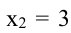
Экстремумы могут быть только в этих точках. Так как при переходе через точку производная меняет знак плюс на минус, то в этой точке функция имеет максимум. При переходе через точку 
производная меняет знак минус на плюс, поэтому в точке у функции минимум. Вычислив значения функции в точках и найдем экстремумы функции: максимум f(2) = 14 и минимум f(3) =13.
Пример:
Нужно построить прямоугольную площадку возле каменной стены так, чтобы с трех сторон она была отгорожена проволочной сеткой, а четвертой стороной примыкала к стене. Для этого имеется а погонных метров сетки. При каком соотношении сторон площадка будет иметь наибольшую площадь?
Решение:
Обозначим стороны площадки через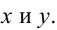 
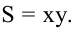
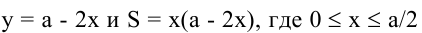
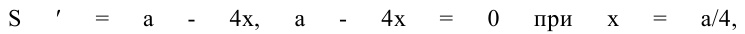
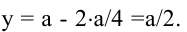
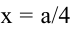
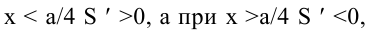
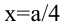
Площадь площадки равна 
Пусть у — это длина стороны, примыкающей к стене. Тогда по условию должно выполняться равенство 2х + у = а. Поэтому 
(длина и ширина площадки не могут быть отрицательными). 
откуда 
Поскольку 
— единственная критическая точка, проверим, меняется ли знак производной при переходе через эту точку. При 
значит, в точке 
функция S имеет максимум. Значение функции 
Поскольку S непрерывна на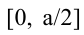 
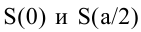
и ее значения на концах 
равны нулю, то найденное значение будет наибольшим значением функции.
Таким образом, наиболее выгодным соотношением сторон площадки при данных условиях задачи является у = 2х.
Пример:
Требуется изготовить закрытый цилиндрический бак вместимостью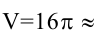 
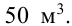
Каковы должны быть размеры бака (радиус R и высота Н), чтобы на его изготовление пошло наименьшее количество материала?
Решение:
Площадь полной поверхности цилиндра равна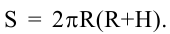 
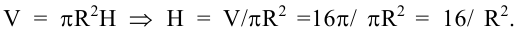
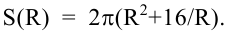
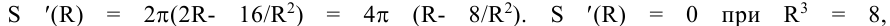
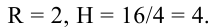
Мы знаем объем цилиндра 
Значит, 
Находим производную этой функции:
следовательно, 
Экстремумы функции
Введём несколько новых понятий. Окрестностью точки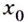 
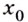
называется любой промежуток, для которого 
является внутренней точкой.
Точка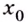 
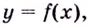
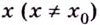
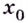
называется точкой минимума (максимума) функции 
если для всех 
из некоторой окрестности точки 
выполняется неравенство 
Точки минимума и максимума обозначают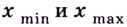 
соответственно.
Значение функции в точке минимума называется минимумом функции, а в точке максимума — максимумом функции. Обозначают их: 
Точки минимума и максимума функции называют точками экстремума (лат. extremum — край, конец). Значения функции в точках её экстремума — её экстремальные значения, или экстремумы.
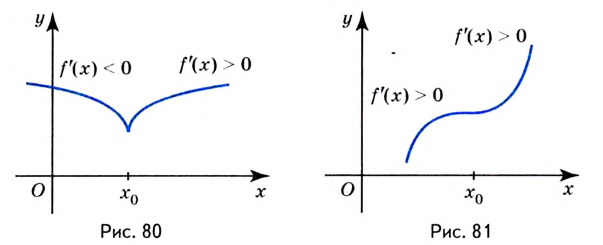
Например, для функции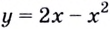 
точка 
является точкой максимума (рис. 77). Её максимум: 
Для функции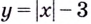 
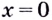
точка 
является точкой минимума (рис. 78). Её минимум: 
Функция, график которой изображён на рисунке 75, имеет четыре экстремальные точки: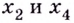 
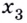
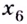
— точки максимума; 
и 
— точки минимума.
Точка экстремума функции не может принадлежать промежутку, на котором эта функция возрастает или убывает (почему?). Следовательно, те точки, в которых производная функции положительная или отрицательная, не могут быть точками её экстремума. Все остальные точки области определения функции являются её критическими точками. Поэтому точками экстремума функции могут быть только её критические точки. Это — необходимое условие существования экстремума.
Выбрать из критических точек функции точки экстремума позволяет достаточное условие существования экстремума.
Пусть функция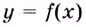 
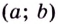
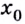
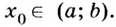
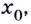
непрерывна на промежутке 
и 
— её критическая точка, 
Тогда: точка 
при переходе через которую в направлении роста аргумента производная меняет знак с «плюса» на «минус», является точкой максимума, а точка, при переходе через которую производная меняет знак с «минуса» на «плюс» — точкой минимума.
Действительно, если производная функции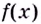 
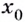
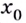
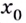
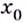
отрицательная, то при переходе через точку 
возрастание функции изменяется на убывание (рис. 79). В этом случае 
— точка максимума. Если же при переходе через точку 
убывание функции изменяется на возрастание, то 
— точка минимума (рис. 80).
Если же производная функции в точке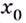 
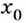
равна нулю, а слева и справа от 
производная функции положительная (рис.81) или слева и справа отрицательная, то 
не является точкой экстремума.
- Заказать решение задач по высшей математике
Пример №552
Найдите точки экстремума и экстремальные значения функции 
Решение:
Критические точки функции: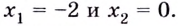 
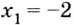
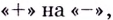
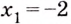
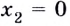
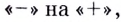
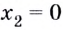
При переходе через точку 
производная меняет знаке 
поэтому 
—точка максимума. При переходе через точку 
производная меняет знак с 
поэтому 
— точка минимума (рис. 82).
Ответ. 
Нахождение экстремумов функции можно оформлять в виде таблицы, как на с. 176. Особенно это удобно при общем исследовании функции, когда находят не только её экстремумы, но и другие свойства, строят её график.
Чтобы исследовать функцию, можно пользоваться следующей схемой:
- найти область определения функции;
- исследовать функцию на чётность, нечётность, периодичность;
- найти точки пересечения графика функции с осями координат;
- исследовать функцию на монотонность, то есть найти промежутки возрастания и убывания функции;
- найти точки экстремума и экстремальные значения функции;
- найти асимптоты графика функции;
- построить график функции.
Пример №553
Исследуйте функцию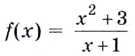 
и постройте её график.
Решение:
Область определения функции — все действительные числа, кроме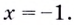 
Поскольку она не симметрична относительно нуля, то функция не может быть чётной или нечётной. Функция непериодическая.
Уравнение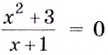 
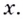
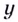
не имеет решений, поэтому график функции не пересекает ось 
Ось 
он пересекает в точке с ординатой 
Критические точки: 
Составим и заполним таблицу.
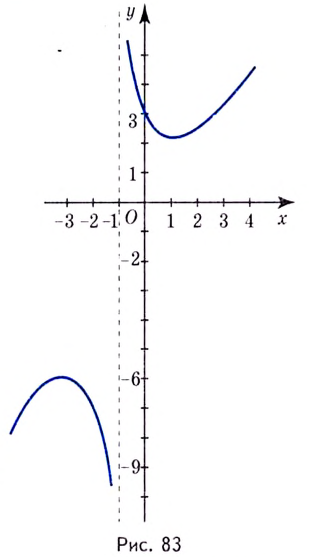
На промежутках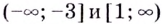 
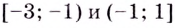
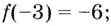
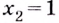
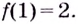
функция возрастает, на промежутках 
функция убывает. 
— точка максимума, 
—точка минимума, 
Область значений функции: 
График функции имеет вертикальную асимптоту 
так как 
График этой функции изображён на рисунке 83.
Пример №554
Может ли нечётная функция иметь экстремум в точке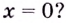 
А чётная функция?
Решение:
Нечётная функция не может. Если в окрестности точки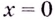 
функция имеет экстремум, то с одной стороны от нуля она возрастает, а с другой — убывает, или наоборот. А нечётная функция — или только возрастает, или только убывает в окрестности точки 
Чётная функция может. Например, функция 
Пример №555
Существуют ли такие числа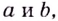 
при которых имеет экстремум функция 
Решение:
При любых действительных значениях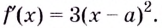 
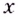
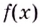
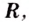
В каждой точке 
производная данной функции неотрицательная. Функция 
возрастает на 
поэтому не может иметь экстремумов.
Ответ. Не существуют.
Пример №556
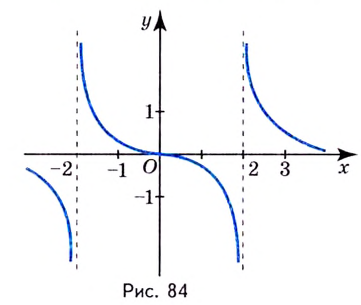
Исследуйте функцию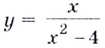 
и постройте её график.
Решение. 
2) Функция — нечётная, поскольку 
Следовательно, её график симметричен относительно начала координат и достаточно исследовать функцию на промежутке 
3) если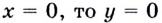 
— график пересекает оси координат только в точке 
4) Найдём производную функции:
Очевидно, что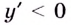 
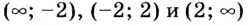
для всех х из области определения. Следовательно, функция убывает на каждом из промежутков 
и не имеет максимумов и минимумов.
Для более точного построения вычислим значение функции в нескольких точках:
График функции имеет вертикальные асимптоты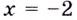 
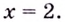
и 
(Убедитесь самостоятельно.)
График функции изображён на рисунке 84.
- Методы решения систем линейных алгебраических уравнений (СЛАУ)
- Скалярное произведение и его свойства
- Векторное и смешанное произведения векторов
- Преобразования декартовой системы координат
- Определитель матрицы
- Критерий совместности Кронекера-Капелли
- Формулы Крамера
- Матричный метод
Дата публикации: 09 апреля 2017.
Урок на тему: «Нахождение точек экстремумов функций. Примеры»
Дополнительные материалы
Уважаемые пользователи, не забывайте оставлять свои комментарии, отзывы, пожелания! Все материалы проверены антивирусной программой.
Скачать:
Нахождение точек экстремумов функций (PDF)
Что будем изучать:
1. Введение.
2. Точки минимума и максимума.
3. Экстремум функции.
4. Как вычислять экстремумы?
5. Примеры.
Введение в экстремумы функций
Ребята, давайте посмотрим на график некоторой функции:
Заметит, что поведение нашей функции y=f (x) во многом определяется двумя точками x1 и x2. Давайте внимательно посмотрим на график функции в этих точках и около них. До точки x2 функция возрастает, в точке x2 происходит перегиб, и сразу после этой точки функция убывает до точки x1. В точке x1
функция опять перегибается, и после этого — опять возрастает. Точки x1 и x2 пока так и будем называть точками перегиба. Давайте проведем касательные в этих точках:
Касательные в наших точках параллельны оси абсцисс, а значит, угловой коэффициент касательной равен нулю. Это значит, что и производная нашей функции в этих точках равна нулю.
Посмотрим на график вот такой функции:
Касательные в точках x2 и x1 провести невозможно. Значит, производной в этих точках не существует. Теперь посмотрим опять на наши точки на двух графиках. Точка x2 — это точка, в которой функция достигает наибольшего значения в некоторой области (рядом с точкой x2). Точка x1 — это точка, в
которой функция достигает своего наименьшего значения в некоторой области (рядом с точкой x1).
Точки минимума и максимума
Определение: Точку x= x0 называют точкой минимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≥ f(x0).
Определение: Точку x=x0 называют точкой максимума функции y=f(x), если существует окрестность точки x0, в которой выполняется неравенство: f(x) ≤ f(x0).
Ребята, а что такое окрестность?
Определение: Окрестность точки — множество точек, содержащее нашу точку, и близкие к ней.
Окрестность мы можем задавать сами. Например, для точки x=2, мы можем определить окрестность в виде точек 1 и 3.
Вернемся к нашим графикам, посмотрим на точку x2, она больше всех других точек из некоторой окрестности, тогда по определению — это точка максимума. Теперь посмотрим на точку x1, она меньше всех других точек из некоторой окрестности, тогда по определению — это точка минимума.
Ребята, давайте введем обозначения:
ymin — точка минимума,
ymax — точка максимума.
Важно! Ребята, не путайте точки максимума и минимума с наименьшим и наибольшим значение функции. Наименьшее и наибольшее значения ищутся на всей области определения заданной функции, а точки минимума и максимума в некоторой окрестности.
Экстремумы функции
Для точек минимума и максимума есть общей термин – точки экстремума.
Экстремум (лат. extremum – крайний) – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума.
Соответственно, если достигается минимум – точка экстремума называется точкой минимума, а если максимум – точкой максимума.
Как же искать экстремумы функции?
Давайте вернемся к нашим графикам. В наших точках производная либо обращается в нуль (на первом графике), либо не существует (на втором графике).
Тогда можно сделать важное утверждение: Если функция y= f(x) имеет экстремум в точке x=x0, то в этой точке производная функции либо равна нулю, либо не существует.
Точки, в которых производная равна нулю называются стационарными.
Точки, в которых производной функции не существует, называются критическими.
Как вычислять экстремумы?
Ребята, давайте опять вернемся к первому графику функции:
Анализируя этот график, мы говорили: до точки x2 функция возрастает, в точке x2 происходит перегиб, и после этой точки функция убывает до точки x1. В точке x1 у функции опять перегибается, и после этого
функция опять возрастает.
На основании таких рассуждений, можно сделать вывод, что функция в точках экстремума меняет характер монотонности, а значит и производная функция меняет знак. Вспомним: если функция убывает, то производная меньше либо равно нулю, а если функция возрастает, то производная больше либо равна нулю.
Обобщим полученные знания утверждением:
Теорема: Достаточное условие экстремума: пусть функция y=f(x) непрерывна на некотором промежутке Х и имеет внутри промежутка стационарную или критическую точку x= x0. Тогда:
- Если у этой точки существует такая окрестность, в которой при x < x0 выполняется f’(x) < 0, а при x > x0 выполняется f’(x)>0, то точка x0 – точка минимума функции y= f(x).
- Если у этой точки существует такая окрестность, в которой при x < x0 выполняется f ’(x)>0, а при x> x0 выполняется f’(x)<0, то точка x0 – точка максимума функции y=f(x).
- Если у этой точки существует такая окрестность, в которой и слева и справа от точки x0 знаки производной одинаковы, то в точке x0 экстремума нет.
Для решении задач запомните такие правила: Если знаки производных определены то:
Алгоритм исследования непрерывной функции y= f(x) на монотонность и экстремумы:
- Найти производную y’.
- Найти стационарные(производная равна нулю) и критические точки (производная не существует).
- Отметить стационарные и критические точки на числовой прямой и определить знаки производной на получившихся промежутках.
- По указанным выше утверждениям сделать вывод о характере точек экстремума.
Примеры нахождения точки экстремумов
1) Найти точки экстремума функции и определить их характер: y= 7+ 12*x — x3
Решение: Наша функция непрерывна, тогда воспользуемся нашим алгоритмом:
а) y’= 12 — 3x2,
б) y’= 0, при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 — точка минимума функции, точка x= 2 — точка максимума функции.
Ответ: x= -2 — точка минимума функции, x= 2 — точка максимума функции.
2) Найти точки экстремума функции и определить их характер.
Решение: Наша функция непрерывна. Воспользуемся нашим алгоритмом:
а) 
б) в точке x= 2 производная не существует, т.к. на нуль делить нельзя,
Область определения функции: [2; +∞], в этой точки экстремума нет, т.к. окрестность точки не определена. Найдем значения, в которой производная равна нулю:
в) Отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= 3 — точка минимума функции.
Ответ: x= 3 — точка минимума функции.
3) Найти точки экстремума функции y= x — 2cos(x) и определить их характер, при -π ≤ x ≤ π.
Решение: Наша функция непрерывна, воспользуемся нашим алгоритмом:
а) y’= 1 + 2sin(x),
б) найдем значения в которой производная равна нулю: 1 + 2sin(x)= 0, sin(x)= -1/2,
т.к. -π ≤ x ≤ π, то: x= -π/6, -5π/6,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -5π/6 — точка максимума функции.
Точка x= -π/6 — точка минимума функции.
Ответ: x= -5π/6 — точка максимума функции, x= -π/6 — точка минимума функции.
4) Найти точки экстремума функции и определить их характер:
Решение: Наша функция имеет разрыв только в одной точке x= 0. Воспользуемся алгоритмом:
а)
б) найдем значения в которой производная равна нулю: y’= 0 при x= ±2,
в) отметим стационарные точки на числовой прямой и определим знаки производной:
г) посмотрим на наш рисунок, где изображены правила определения экстремумов.
Точка x= -2 точка минимума функции.
Точка x= 2 — точка минимума функции.
В точке x= 0 функция не существует.
Ответ: x= ±2 — точки минимума функции.
Задачи для самостоятельного решения
а) Найти точки экстремума функции и определить их характер: y= 5x3 — 15x — 5.
б) Найти точки экстремума функции и определить их характер:
в) Найти точки экстремума функции и определить их характер: y= 2sin(x) — x при π ≤ x ≤ 3π.
г) Найти точки экстремума функции и определить их характер:
п.1. Алгоритм решения задач на поиск экстремума
Шаг 1. Проанализировать условие задачи, обозначить одно из неизвестных буквой (переменной). Если это удобно, обозначить все неизвестные разными буквами и выбрать «основную» переменную.
Шаг 2. Выразить другие неизвестные через основную переменную.
Шаг 3. Записать функцию от основной переменной.
Шаг 4. Найти производную от полученной функции. Исследовать функцию на экстремум.
Шаг 5. Истолковать результат в соответствии с условием задачи.
Например:
Как разбить число 10 на два слагаемых так, чтобы их произведение было наибольшим?
Пусть (x) — первое слагаемое. Тогда ((10-x)) — второе слагаемое.
Их произведение (f(x)=x(10-x)rightarrow max)
Исследуем полученную функцию на экстремум:
(f'(x)=(10x-x^2)’=10-2x)
(f'(x)=0) при (x=5)
По условию значение (xin [0;10]).
| (x) | [0;5) | 5 | (5;10] |
| (f'(x)) | >0 | 0 | <0 |
| (f(x)) | (nearrow) | max | (searrow) |
Точка максимума (x=5, f_{max}=5cdot (10-5)=25)
Т.е., 10 нужно разбить на две пятерки, которые дадут максимальное возможное произведение 25.
Ответ: 5 и 5, максимальное произведение 25
п.2. Примеры
Пример 1. Какое число в сумме со своим квадратом дает наименьшее значение?
Пусть (x) — данное число.
По условию: (f(x)=x+x^2rightarrow min)
Исследуем полученную функцию на экстремум:
(f'(x)=(x+x^2)’=1+2x)
(f'(x)=0) при (x=-frac12)
По условию значение (xin mathbb{R}).
| (x) | (left(-infty;-frac12right)) | (-frac12) | (left(-frac12;+inftyright)) |
| (f'(x)) | <0 | 0 | >0 |
| (f(x)) | (searrow) | min | (nearrow) |
Точка минимума (x=-frac12, f_{min}=-frac12+left(-frac12right)^2=-frac12+frac14=-frac14)
Ответ: число (left(-frac12right)), минимальная сумма (left(-frac14right))
Пример 2. Какой из прямоугольников, вписанных в круг радиусом R, имеет наибольшую площадь?
 |
Диагонали вписанного прямоугольника являются диаметрами круга: AC=BD=2R Обозначим угол между диагоналями (alpha=angle AOB, 0ltalphalt pi). Используем формулу площади четырехугольника через диагонали: $$ S=frac{d_1d_2}{2}sinalpha=frac{(2R)^2}{2}sinalpha=2R^2sinalpha $$ |
Мы получили площадь как функцию от угла: (S(alpha)=2R^2 sinalpha)
Исследуем полученную функцию на экстремум:
(S'(alpha)=2R^2 cosalpha)
(S'(alpha)=0) при (cosalpha=0Rightarrow alpha=fracpi 2) — прямой угол.
| (alpha) | (left(0;fracpi 2right)) | (fracpi 2) | (left(fracpi 2;piright)) |
| (S'(alpha)) | >0 | 0 | <0 |
| (S(alpha)) | (nearrow) | max | (searrow) |
Точка максимума (alpha=fracpi 2, S_{max}=2R^2sinfracpi 2=2R^2cdot 1=2R^2)
Вписанный прямоугольник с прямым углом между диагоналями – это квадрат (т.к. диагонали перпендикулярны и равны).
Сторона квадрата по теореме Пифагора: (AB^2=OA^2+OB^2=2R^2Rightarrow AB=Rsqrt{2})
Ответ: квадрат со стороной (Rsqrt{2}), максимальная площадь (2R^2)
Пример 3. Какой из прямоугольников, вписанных в круг радиусом R, имеет наибольший периметр?
 |
Диагонали вписанного прямоугольника являются диаметрами круга: AC=BD=2R Обозначим угол между диагоналями (alpha=angle AOB, 0ltalphalt pi). По теореме косинусов сторона AB: begin{gather*} AB^2=OA^2+OB^2-2OAcdot OBcdot cosalpha=\ =R^2+R^2-2R^2cosalpha=2R^2(1-cosalpha)=\ =2R^2cdot 2sin^2fracalpha 2=4R^2sin^2fracalpha 2\ AB=2Rsinfracalpha 2 end{gather*} |
Сторона BC: begin{gather*} BC^2=OB^2+OC^2-2OBcdot OCcdot cos(180^{circ}-alpha)=\ =R^2+R^2+2R^2cosalpha=2R^2(1+cosalpha)=2R^2cdot 2cos^2fracalpha 2=4R^2cos^2fracalpha 2\ BC=2Rcosfracalpha 2 end{gather*} Периметр: begin{gather*} P(alpha)=2(AB+BC)=2left(2Rsinfracalpha 2+2Rcosfracalpha 2right)=4Rleft(sinfracalpha 2+cosfracalpha 2right), 0ltfracalpha 2ltfracpi 2 end{gather*} Исследуем полученную функцию на экстремум: begin{gather*} P'(alpha)=4Rleft(frac12 cosfracalpha 2-frac12 sinfracalpha 2right)=2Rleft(cosfracalpha 2-sinfracalpha 2right)\ P'(alpha)=0Rightarrow cosfracalpha 2-sinfracalpha 2=0Rightarrow sinfracalpha 2=cosfracalpha 2 |: cosfracalpha 2\ tgfracalpha 2=1Rightarrow fracalpha 2=fracpi 4=Rightarrow alpha = fracpi 2 — text{прямой угол} end{gather*}
| (fracalpha 2) | (left(0;fracpi 4right)) | (fracpi 4) | (left(fracpi 4;fracpi 2right)) |
| (P'(alpha)) | >0 | 0 | <0 |
| (P(alpha)) | (nearrow) | max | (searrow) |
Точка максимума (alpha=fracpi 2, P_{max}=4Rleft(sinfracpi 4+cosfracpi 4right)=4Rcdot 2cdot frac{sqrt{2}}{2}=4sqrt{2}R)
Вписанный прямоугольник с прямым углом между диагоналями – это квадрат (т.к. диагонали перпендикулярны и равны).
Сторона квадрата по теореме Пифагора: (AB^2=OA^2+OB^2=2R^2Rightarrow AB=Rsqrt{2})
Ответ: квадрат со стороной (Rsqrt{2}), максимальный периметр (4sqrt{2}R)
Пример 4. Определите размеры открытого бассейна с квадратным дном объемом 32 м3 так, чтобы на облицовку его стен и дна ушло как можно меньше материала.
Пусть сторона бассейна a, высота h. Тогда объем: (V=a^2h=32). Откуда (h=frac{32}{a^2}).
Площадь дна: (S_0=a^2).
Площадь каждой стены: (S_1=ah=acdot frac{32}{a^2}=frac{32}{a}).
Общая площадь для облицовки: begin{gather*} S(a)=S_0+4S_1=a^2+4cdot frac{32}{a}=a^2+frac{128}{a} end{gather*} Исследуем полученную функцию на экстремум: begin{gather*} S'(a)=2a-frac{128}{a^2}=frac{2a^3-128}{a^2}=frac{2(a^3-64)}{a^2}=frac{2(a-4)(a^2+4a+16)}{a^2}\ S'(a)=0 text{при} a=4 end{gather*} По условию (agt 4)
| (a) | (0;4) | 4 | (left(4;+inftyright)) |
| (S'(a)) | <0 | 0 | >0 |
| (S(a)) | (searrow) | min | (nearrow) |
Точка минимума (a=4) $$ S_{min}=4^2+frac{128}{4}=16+32=48 (м^2) $$ Оптимальные размеры бассейна: сторона (a=4) м, высота (h=frac{32}{16}=2) м
Ответ: бассейн со стороной 4 м и высотой 2 м,
минимальная площадь облицовки 48 м2.
Пример 5*. Найдите наибольшей объем конуса с образующей a.
 |
По условию AB=a Обозначим угол при основании (alpha=angle BAO, 0ltalphalt fracpi 2). Тогда: (r=OA=ABcdot cosalpha=acosalpha) (h=OB=ABcdot sinalpha=asinalpha) Объем конуса: begin{gather*} V=frac13 Sh=frac13cdotpi r^2h=fracpi 3cdot a^2cos^2alphacdot asinalpha=\ =frac{pi a^3}{3}cos^2alpha sinalpha end{gather*} |
Объем как функция угла при основании: (V(alpha)=frac{pi a^3}{3}cos^2alpha sinalpha)
Исследуем полученную функцию на экстремум: begin{gather*} V'(alpha)=frac{pi a^3}{3}((cos^2alpha)’sinalpha+cos^2alpha sin’alpha)=frac{pi a^3}{3}(-2cosalphacdot sin^2alpha+cos^3alpha)=\ =frac{pi a^3}{3}cosalpha(cos^2alpha-2sin^2alpha)=frac{pi a^3}{3}cosalpha(cos^2alpha-2(1-cos^2alpha))=\ =frac{pi a^3}{3}cosalpha(3cos^2alpha-2) end{gather*} Решаем уравнение (V'(alpha)=0Rightarrow cosalpha(3cos^2alpha-2)=0Rightarrow left[ begin{array}{l} cosalpha=0\ 3cos^2alpha-2=0 end{array} right. )
(cosalpha=0) дает (alpha=fracpi 2) — это корень не подходит.
Решаем второе уравнение: (3cos^2alpha-2=0Rightarrow cos^2alpha=frac23Rightarrow cosalpha=pmsqrt{frac23})
Для (0ltalphaltfracpi 2) выбираем положительное значение (cosalpha=sqrt{frac23})
Тогда (sinalpha=sqrt{1-cos^2alpha}=sqrt{1-frac23}=frac{1}{sqrt{3}})
| (alpha) | (left(0;arccossqrt{frac23}right)) | (arccossqrt{frac23}) | (left(arccossqrt{frac23};fracpi 2right)) |
| (V'(alpha)) | >0 | 0 | <0 |
| (V(alpha)) | (nearrow) | max | (searrow) |
Точка максимума (alpha=arccossqrt{frac23}, V_{max}=frac{pi a^3}{3}cdotfrac23cdotfrac{1}{sqrt{3}}=frac{2pi a^3}{9sqrt{3}})
Ответ: максимальный объем (V_{max}=frac{2pi a^3}{9sqrt{3}})
Пример 6. В данный конус вписан цилиндр наибольшего объема. Найдите отношение высоты конуса к высоте этого цилиндра.
 |
Пусть R — радиус конуса, H — высота конуса, r — радиус цилиндра, h — высота цилиндра. R и H — постоянные, r и h — переменные. Исходя из симметрии, задача сводится к вписыванию в равнобедренный треугольник ΔABC, AB=BC прямоугольника DEFG наибольшей площади. |
 |
По двум углам (triangle ABOsimtriangle ADG) $$ frac{BO}{DG}=frac{AO}{AG}Rightarrow frac Hh=frac{R}{R-r}Rightarrow h=Hfrac{R-r}{R} $$ Площадь прямоугольника: begin{gather*} S=GFcdot DG=2rcdot h=2rcdot Hfrac{R-r}{R}\ S(r)=frac{2Hr(R-r)}{R} end{gather*} |
Исследуем полученную функцию на экстремум: begin{gather*} S'(r)=frac{2H}{R}(Rr-r^2)’=frac{2H}{R}(R-2r)\ S'(r)=0 text{при} r=frac R2 end{gather*} По условию (0lt rlt R)
| (r) | (left(0;frac R2right)) | (frac R2) | (left(frac R2; Rright)) |
| (S'(r)) | >0 | 0 | <0 |
| (S(r)) | (nearrow) | max | (searrow) |
Точка максимума (r=frac R2)
Искомое отношение в точке максимума: $$ frac Hh=frac{R}{R-r}=frac{R}{R-frac R2}=2 $$
Ответ: 2
Пример 7*. Из трех досок одинаковой ширины сколачивается желоб. При каком угле наклона стенок площадь поперечного сечения желоба будет наибольшей?
 |
Пусть AB=BC=CD=d Искомый угол (alpha=angle ABC). ABCD — равнобедренная трапеция (S_{ABCD}rightarrow max) |
Выразим площадь трапеции через угол.
Найдем диагональ AC по формуле косинусов: begin{gather*} AC^2=AB^2+BC^2-2ABcdot BCcdot cosalpha=d^2+d^2-2d^2cosalpha=2d^2(1-cosalpha)=\ =2d^2cdot 2sin^2fracalpha 2=4d^2sin^2fracalpha 2\ AC=sqrt{4d^2sin^2fracalpha 2}=2dsinfracalpha 2 end{gather*} Заметим, что (angle ACD=angle BCD-angle BCA=alpha-left(90^circ-fracalpha 2right)=frac{3alpha}{2}-90^circ)
Площадь трапеции: begin{gather*} S_{ABCD}=S_{ABC}+S_{ACD}=frac12 ABcdot BCcdot sinalpha+frac12 ACcdot CDcdot sinangle ACD=\ =frac12left(d^2sinalpha+2dsinfracalpha 2cdot 2cdot sinleft(frac{3alpha}{2}-90^circright)right)=frac{d^2}{2}left(sinalpha+2sinfracalpha 2 sinleft(frac{3alpha}{2}-90^circright)right)=\ =frac{d^2}{2}left(sinalpha-2sinfracalpha 2 cosfrac{3alpha}{2}right)=frac{d^2}{2}left(sinalpha-sinleft(fracalpha 2+frac{3alpha}{2}right)+sinleft(fracalpha 2-frac{3alpha}{2}right)right)=\ =frac{d^2}{2}(sinalpha-(sin2alpha-sinalpha))=frac{d^2}{4}(2sinalpha-sin2alpha)=\ =frac{d^2}{4}(2sinalpha-2sinalpha cosalpha)=frac{d^2}{2}sinalpha(1-cosalpha) end{gather*} Полученная функция: $$ S(alpha)=frac{d^2}{2}sinalpha(1-cosalpha) $$ Исследуем на экстремум: begin{gather*} S'(alpha)=frac{d^2}{2}(sin’aalpha(1-cosalpha)+sinalpha(1-cosalpha)’)=\ =frac{d^2}{2}(cosalpha(1-cosalpha)+sin^2alpha)=frac{d^2}{2}(cosalpha-cos^2alpha+1-cos^2alpha)=\ =frac{d^2}{2}(1+cosalpha-2cos^2alpha) end{gather*} Решаем уравнение begin{gather*} S'(alpha)=0Rightarrow 1+cosalpha-2cos^2alpha=0\ 2cos^2alpha-cosalpha-1=0 end{gather*} Замена: (t=cosalpha, |t|leq 1) begin{gather*} 2t^2-t-1=0Rightarrow (2t+1)(t-1)=0Rightarrow left[ begin{array}{l} t=-frac12\ t=1 end{array} right. end{gather*} Возвращаемся к исходной переменной. По условию (0lt alphaltpi). begin{gather*} left[ begin{array}{l} cosalpha=-frac12\ cosalpha=1 end{array} right. Rightarrow left[ begin{array}{l} a=frac{2pi}{3}\ a=0 — text{не подходит} end{array} right. end{gather*}
| (alpha) | (left(0;frac{2pi}{3}right)) | (frac{2pi}{3}) | (left(frac{2pi}{3};piright)) |
| (S'(alpha)) | >0 | 0 | <0 |
| (S(alpha)) | (nearrow) | max | (searrow) |
Точка максимума (alpha=frac{2pi}{3})
Максимальная площадь поперечного сечения $$ S_{max}=frac{d^2}{2}sinfrac{2pi}{3}left(1-cosfrac{2pi}{3}right)=frac{d^2}{2}cdot frac{sqrt{3}}{2}cdotleft(1+frac12right)=frac{3sqrt{3}}{8}d^2 $$ Желоб нужно делать с углом (frac{2pi}{3} (120^circ))
Ответ: (frac{2pi}{3})
Как найти точки минимума и максимума функции
Содержание:
-
Минимум и максимум функции
- Точка минимума, минимум функции
- Точка максимума, максимум функции
- Исследование функций на экстремумы
- Примеры задач
Минимум и максимум функции
Минимумом и максимумом функции, другими словами экстремумами, называют точки, в которых функция меняет характер монотонности (с возрастания на убывание и наоборот). Важно понимать, что экстремумы это не максимальные и минимальные значения функции. Обозначаются следующим образом:
- (y_{min}, y_{max}) — минимум, максимум функции или экстремумы;
- (x_{min}, x_{max}) — точки минимума, максимума функции;
- (y_{наиб}, y_{наим}) — наибольшее (максимальное), наименьшее (минимальное) значение функции.
Точка минимума, минимум функции
Точка минимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)geq f(x_0))
Минимум функции — значение функции в точке минимума (x_0)
Осторожно! Если преподаватель обнаружит плагиат в работе, не избежать крупных проблем (вплоть до отчисления). Если нет возможности написать самому, закажите тут.
Простыми словами, точка минимума — это та, где убывание функции меняется на возрастание.
Точка максимума, максимум функции
Точка максимума — такая точка (x_0), если у неё существует окрестность, для всех точек которой выполняется неравенство (f(x)leq f(x_0))
Максимум функции — значение функции в точке максимума (x_0)
Простыми словами, точка максимума — это та, где возрастание функции меняется на убывание.
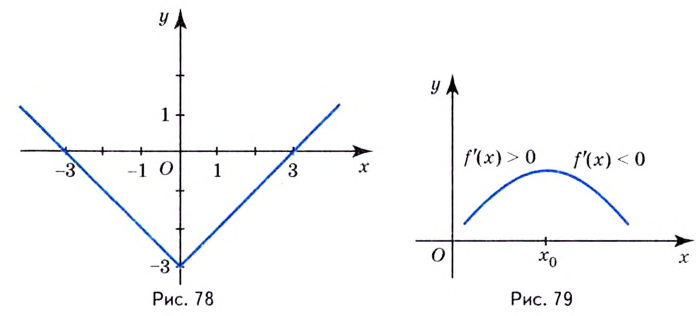
Точки максимума и минимума на графике:
Исследование функций на экстремумы
Теорема. Если функция f(x) имеет экстремум в точке (x=x_0,) то в ней производная либо равна 0, либо не существует.
Алгоритм нахождения экстремумов с помощью производной:
-
Найти область определения функции — D(y).
-
Определить производную — f ‘(x).
-
Определить стационарные точки y = f(x), т.е. те, которые принадлежат D(y), f ‘(x) в них обращается в ноль, отыскать критические точки, в которых производной не существует (пример: (f^,(x)=frac1{2sqrt x}), производной не существует при x = 0).
-
Исследовать характер изменения функции f (x) и знак f ‘(x) в промежутках, на которые найденные критические точки делят область определения (при отрицательном знаке производной функция убывает, при положительном — возрастает).
-
Относительно каждой критической точки определить, является ли она точкой максимума, минимума (возрастание меняется на убывание — точка максимума, убывание на возрастание — минимума) или не является точкой экстремума (то есть, меняется ли знак производной при переходе через исследуемую точку).
-
Вычислить значения функции в точках экстремума.
Примеры задач
Задача 1
Исследовать на экстремумы функцию (f(x)=x^3-3x^2.)
Решение задачи по алгоритму:
1) (D(y): xin(-infty;+infty)), т.е. x — любое число.
2) Производная: (f'(x)=3x^2-6x) .
3) Из пункта 1 следует, что критических точек нет. Найдем стационарные:
Приравниваем f ‘(x) к 0, решаем квадратное уравнение (3x^2-6x=0), получаем (x_1=0),(;x_2=2.)
4) Отметим на горизонтальной оси координат точки 0 и 2. Подставим любое x из интервала ((-infty;0)) в f'(x), например, пусть x = -1, тогда (f'(x)=3{(-1)}^2-6(-1)=3+6=9). Получаем f ‘(x)>0, значит на исследуемом интервале f(x) возрастает. Аналогично рассмотрим оставшиеся интервалы. Итого, на отрезке (0;2) производная отрицательна, функция убывает, а на интервале ((2;+infty)) производная положительна, возрастает. Из этого следует, что x=0 — точка максимума, а x=2 — минимума.
5) Найдем значение экстремумов функции.
(f(0)=0-3times0=0)
(f(2)=2^3-3times2^2=8-12=-4)
Ответ: (x_{min}=2,;y_{min}=-4;;x_{max}=0,;y_{max}=0) или (0;0) — минимум функции, (2;-4) — максимум.
Задача 2
Найти промежутки монотонности функции (f(x)=frac x{x^2-4}).
1) (D(y): xinmathbb{R},;)кроме(;pm2)
2) (f'(x)=frac{1(x^2-4)-xtimes2x}{{(x^2-4)}^2}=-frac{x^2+4}{{(x^2-4)}^2})
3) Итак, как выяснилось в пункте 1, критические точки 2 и -2. Если мы приравняем f ‘(x) к 0, чтобы найти стационарные точки, то увидим, что уравнение не будет иметь корней. Значит, стационарных точек нет. Из этого следует, что функция монотонна на всей области определения. Проверим, возрастает она или убывает. Для этого решаем неравенство (-frac{x^2+4}{{(x^2-4)}^2}leq0) и получим, что неравенство верно при любом x, значит функция убывает.
Не забываем, что в ответе, указывая промежуток, обязательно нужно исключить критические точки -2 и 2 т.к. в них функция не определена.
Ответ: f(x) убывает на промежутке ((-infty;-2)cup(-2;2)cup(2;+infty)).
Задача 3
Докажите, что функция (f(x)=x^5+2x^3-4) возрастает на всех числовой прямой.
1) (D(y): xinmathbb{R}), значит критических точек нет.
2) (f'(x)=5x^4+6x)
3) Приравняем f'(x) к 0 и найдем корень: x = 0. Отметим 0 на числовой прямой и определим знак производной на промежутках ((-infty;0)) и ((0;+infty)). Получим, что производная положительна на обоих промежутках, следовательно функция возрастает на всей числовой прямой.
Утверждение доказано